a) Har han han rätt? motivera

b) vad är friktion
/zuber nur o, sia skolan

Svar:
a Ja, han har rätt. Om du sätter underskruv på bollen (nedsidan av bollen rör sig i kastriktningen), så kommer bollen att komma tillbaka efter studs (eftersom kontaktytan med golvet rör sig framåt kommer friktionen ge en kraft bakåt).

Sidoskruv får bollen att studsa åt sidan. Skruvade bollar används i de flesta bollsporter: golf, tennis, fotboll...

Se nedanstående video med skruvade bollar.

b Se fråga 16025 om friktion.
/Peter E

Nyckelord: friktion [53]; skruvad boll [10];

Svar:
Rullmotstånd, som ibland kallas rullfriktion, är det motstånd som uppstår när ett runt föremål såsom en boll eller ett däck rullar på en plan yta. Det orsakas främst av deformation av föremålet (hjulet) och/eller underlaget. Ytterligare bidragande faktorer är hjulets radie och dess fart framåt samt vidhäftning och slip mellan ytorna. (Rullmotstånd )

Det finns enkla formler för olika rullmotstånd, se ovanstående Wikipedia-artikel. Problemet är att formlerna innehåller parametrar som måste bestämmas genom experiment.

Se fråga 14921 och 16025 för motsvarande formler för "vanlig" friktion (glidmotstånd).
/Peter E

Nyckelord: friktion [53];

Svar:
Det enklaste är att göra de båda ytorna skrovliga. Detta gör friktionskoefficienten (se fråga 14921 ) större.

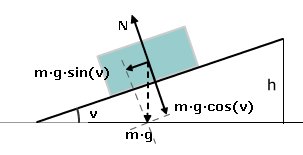
Man kan även öka friktionen genom att öka normalkraften (se fråga 14921 ). Detta kan man för ett fordon åstadkomma med vingar eller spoilers som trycker ner fordonet mot underlaget.

Se även fråga 16025 .
/Peter E

Nyckelord: friktion [53];

För det mesta kyler ju luft när man rör sig i den. Men tittar man på farkoster och andra föremål som skall bryta sig genom vår atmosfär börjar de glöda eller till och med brinna upp.

Vid vilken hastighet har vi ett nolläge där temperaturen vare sig ökar eller minskar? Låt oss för enkelhetens skull säga att befinner oss i luft vid havsnivån.

Mvh Niclas
/Niclas W, Stenbocksskolan, Ulricehamn

Svar:
Aerodynamic heating (aerodynamisk uppvärmning) is the heating of a solid body produced by its high-speed passage through air (or by the passage of air past a test object in a wind tunnel), whereby its kinetic energy is converted to heat by skin friction on the surface of the object at a rate that depends on the viscosity and speed of the air. In science and engineering, it is most frequently a concern regarding meteors, reentry vehicles, and the design of high-speed aircraft. (Aerodynamic_heating )

För överljudshastigheter är uppvärmning ett problem eftersom utsatta delar måste kylas. För standardplan (hastigheter mindre än 800 km/t) är uppvärmningen inget problem.

Se fråga 12765 för information om vindavkylning.
/Peter E

Nyckelord: friktion [53]; kylning [7]; vindavkylning [4];

Svar:
Luftmotståndet är mycket mindre än motsvarande i vatten.

Figuren nedan från fråga 15385 ger ett uttryck för fallhastigheten (gränshastigheten) i en fluid (vätska eller gas, se Fluid ). Som synes är fallhastigheten omvänt proportionell mot roten ur fluidens densitet r. Stor densitet (vatten) ger då lägre fallhastighet än låg densitet (luft).

Med ungefärliga värden på densiteten för vatten och luft får vi förhållandet i fallhastighet

sqrt(1000/1) = sqrt(1000) = 32

Nyckelord: fallrörelse [31]; friktion [53]; luftmotstånd [11]; gränshastighet [4];

I vilken backe kommer jag att rulla snabbast och komma ner till marken först? Och vad beror detta på? Vilka krafter och motstånd gör så att jag får olika resultat?
/Jacob Å, Framtidskompassen Vellinge, Vellinge

Svar:
Den accelererande komposanten till tyngdkraften blir större för en brantare backe. Den bromsande kraften f blir mindre eftersom normalkraften N blir mindre med ökande lutning. Båda ger alltså högre hastighet för ökande branthet.

Vad det beror på? Ja, krafterna är kända så det är bara att räkna. I fråga 20174 finns en lösning för ett lite mer komplicerat problem.

Nyckelord: friktion [53];

Svar:
Om en kloss rör sig på en yta kommer atomer/molekyler på ytan att kollidera och rivas loss. Arbetet som utförs av kraften som driver klossen blir till oordnad rörelse, dvs värme.

Om temperaturen överstiger absoluta nollpunkten kommer elektromagnetisk strålning att sändas ut enligt Plancks strålningslag, se fråga 12397 och länk 1. Om ytan har högre temperatur än omgivningen kommer vi att få en nettotransport av värme ut från det varmare området.

Se även fråga 16025 och Wikipedia-artikeln Friktion .
/Peter E

Nyckelord: friktion [53];

1 http://hyperphysics.phy-astr.gsu.edu/hbase/mod6.html

Svar:
Jag förstår inte resultatet av ditt experiment. De flesta ämnen utom mymetall (se fråga 2720 ) släpper igenom magnetfält. Gemet bör då följa med magneten om du har en plastplatta emellan.

För små rörelser i längdriktningen av gemet kan jag tänka mig att gemet inte flyttar sig på grund av friktion. Friktionskraften (se fråga 16025 ) ökar ju eftersom attraktionen mellan magneten och gemet ökar normalkraften.
/Peter E

Nyckelord: magnetism [52]; friktion [53];

Svar:
Arbetet är lika stort bara om du kan bortse från friktion. Om du har friktion får du förluster som blir till värmeenergi. Arbetet går alltså till att lyfta föremålet och att motverka friktionen. Se fråga 20415 för ett genomräknat exempel.
/Peter E

Nyckelord: lutande plan [15]; friktion [53];

Ursprunglig fråga:
Om man drar en låda med konstant hastighet uppför ett lutande plan och ska undersöka verkningsgraden för olika vinklar. Arbetet ses som den tillförda energin och lägesenergin ses som den nyttiga energin.

Våra resultat visar att större vinklar ger större verkningsgrad. Är detta sant? Varför/varför inte?
/Denizé Z, TBS, Örebro

Svar:
För att dra lådan uppför planet krävs en kraft som är lika med summan av friktionskraften µ·N=µ·m·g·cos(v) och tyngdkraftens komposant m·g·sin(v), alltså dragkraften, se länk 1 och nedanstående figur från länk 1:

F = µ·m·g·cos(v) + m·g·sin(v)

Potentiell energi på höjden h: mgh

Arbete: (µ·m·g·cos(v) + m·g·sin(v))·h/sin(v)

Verkningsgrad = e = Potentiell energi/Arbete

e = sin(v)/((µ·cos(v) + sin(v)) = 1/(µ·cot(v) + 1)

Låt oss se om detta är rimligt. Utan friktion (µ=0) ger e=1 som sig bör.

Om vinkeln v=0^o blir e=0. Om v=90^o blir e=1. Dessa extremfall motsvarar mycket friktion (lång sträcka, hög normalkraft) och ingen friktion (lådan dras vertikalt utan att röra planet).

Om v=45^o och µ=0.2 blir e=1/(0.2+1)=0.83.

Som du ser är det korrekt att stor vinkel ger högre verkningsgrad.

Nyckelord: friktion [53]; lutande plan [15];

1 http://www.kursnavet.se/kurser/fy1201/fy1201w/M1_1_0_070-friktion-lutande.htm

Svar:
Friktion är ett mycket komplicerat begrepp, se Friction . Friktionen mellan t.ex. en kloss och underlaget beror på ytornas struktur. Om ytorna är ojämna (sandpapper) hakar ojämnheterna i varandra och man får mycket friktion. Släta ytor (metall, is) har i allmänhet liten friktion eftersom det inte finns något som hindrar klossens rörelse.

För ämnen med stor friktion kan man minska denna med smörjmedel, t.ex. olja, tvål eller vatten. Smörjmedel gör att klossen lyfts lite grann, så att ojämnheterna inte kan gripa in i varann.

Vad gäller fuktiga bomullsbyxor så väntar man sig större friktion än med galonbyxor eftersom vattnet sugs upp och fastnar i tyget, och kan inte bilda ett smörjande lager mellan byxan och underlaget.

Se även fråga 14921 , 13746 och 16025 . Inledningen till Wikipedia-artikeln om friktion är mycket bra: Friktion .
/Peter E

Nyckelord: friktion [53];

Svar:
Lina! Det grundläggande med ett lutande plan är att lägesenergi omvandlas till rörelseenergi. En komplikation är att man ofta behöver ta hänsyn till friktionsförluster. För ett glidande föremål använder du den vanliga friktionskoefficienten. I detta fallet är det ojämnheter i föremålet och i underlaget som ger en bromsande kraft.

För ett hjul eller en kula har man vad som kallas rullmotstånd, se Rullmotstånd . Detta uppstår genom att normalkraften deformerar kulan/hjulet och/eller underlaget. Matematiskt behandlas rullmotstånd som friktion och friktionskraften ges av det vanliga uttrycket F=mN.

För att en kula eller ett hjul skall rulla på en yta behövs friktion. Man antar normalt att friktionen är tillräcklig så att kulan/hjulet inte glider alls.

Det tillkommer emellertid lite komplikationer för rullande föremål. För det första kommer en del av rörelseenergin som skapas av det lutande planet att bli till rotationsenergi. I fråga 14738 visas att rotationsenergi och rörelseenergi för en homogen kula förhåller sig som 2:5.

Dessutom kan föremålet både glida och rulla (bromsande bil). Då blir det riktigt besvärligt och risk att eleverna flyr.
/Peter E

Nyckelord: friktion [53]; lutande plan [15];

Ursprunglig fråga:
Hej, under våra fysikspecialiserings lektioner har vi diskuterat teorin bakom detta experiment, utan framgång. Hur ser en förklaring/teori ut?

https://www.youtube.com/watch?v=5ZnKIPfIhAQ&nohtml5=False
/Gabrielle J, Haganässkolan, Osby

Svar:
Fritt fall med löst rep

För det första: detta är fullständigt livsfarligt om man inte gör det rätt! Rätt utfört är det en utmärkt demonstration av rörelsemängdsmomentets bevarande (se fråga 12527 ) och friktion.

För en tyngd med massan m som snurras runt i ett snöre med längden r och med hastigheten v är rörelsemängdsmomentet

L = m*v*r

(Egentligen är L en vektor, men låt oss inte krångla till det.)

Massan är naturligtvis konstant, så om r minskar måste v öka för att L skall vara konstant. Allteftersom linan med tyngden roterar kring den horisontella stolpen blir ju r mindre. I början glider ju repet mot stolpen, vilket även det gör att r minskar. För att rörelsemängdsmomentet skall bevaras måste alltså tyngdens hastighet öka. Detta innebär två saker som är väsentliga:

1 Tyngden snurrar snabbare och snabbare runt stolpen och många varv runt stolpen hindrar att linan glider.

2 Den ökande hastigheten gör att spänningen i linan ökar (F=mv²/r).

Både 1 och 2 medför att friktionen ökar vilket bromsar upp gubben. Den ökande hastigheten bidrar till att gubben hinner bromsas in innan han slår i marken.

Längden på linan, friktionen mellan rep/stolpe och massan hos vikten måste anpassas så att gubben bromsas upp lagom fort. För mycket uppbromsning gör att gubben dras sönder av linan, för liten uppbromsning och gubben slår i marken.

Här är videon. Man ser att det i princip är fråga om ett bungyjump med översta ändan lös och utan elasticitet i linan.

Nyckelord: rörelsemängdsmoment [14]; friktion [53];

1 https://www.youtube.com/watch?v=5ZnKIPfIhAQ&nohtml5=False

A: Vilken fart har tegelpannan när den rutschar av taket?

B: Använd svaret från "A" för att beräkna hur lång långt ut från husväggen som tegelpannan träffar marken. Det är 4 m från takkanten till marken.

Nu del A tror jag att jag har klarat fick 4,5m/s genom att likställa rörelseenergi med läges där h=s*sin(v). men det finns inget facit är otroligt tacksam för hjälp och vägledning. Glad påsk!
/edin R

Svar:
Uppgiften kommer från länk 1. Eftersom problemet innehåller friktion kan du inte använda energikonservering utan friktionsförluster (se emellertid nedan). ________________________________________________________________

A Vi börjar med att beräkna den resulterande kraften F_r från skillnaden mellan tyngdkraftens komponent nedåt parallellt med planet och friktionskraften, se figur nedan:

F_r = mg(sinq - m*cosq) = mg(sin(25) - 0.2*cos(25)) = mg*0.2414 N

Accelerationen a ges av

a = F/m = g*0.2414 = 9.81*0.2414 = 2.368 m/s²

Vi räknar ut tiden t på planet från

s = at²/2

t = sqrt(2*s/a) = sqrt(2*5/2.368) = 2.055 s

Sluthastigheten vid takets slut blir då

v = a*t = 2.368*2.055 = 4.866 m/s

Låt oss kolla detta svar genom att tillämpa energins bevarande

Potentiella energin i startläget är

mgh = m*9.81*sinq *5 = m*9.81*sin(25)*5 = 20.73m J

Rörelseenergin på takkanten blir

E_k = m*v²/2 = m*4.866²/2 = 11.84m J

Friktionsförlusterna är

E_f = kraften*vägen = mg*m*cosq*5 = m*9.81*0.2*cos(25)*5 = 8.89m J

Summan av E_f och E_k blir

8.89m + 11.84m = 20.73m J

vilket stämmer bra med potentiella energin ovan. ________________________________________________________________

B Vi delar vi upp hastigheten vid takkanten i en horisontell och en vertikal komponent:

v_h0 = v₀*cos(25) = 4.866*cos(25) = 4.410 m/s

v_v0 = v₀*sin(25) = 4.866*sin(25) = 2.056 m/s

För rörelsen i vertikalled (fritt fall) gäller (ekv. 4 i fråga 18438 )

v_v² = v_v0² + 2as = 2.056² + 2*9.81*4 = 82.71 (m/s)²

dvs

v_v = 9.095 m/s

Vi räknar ut falltiden t från

s = v_v0*t + gt²/2 = 2.056*t + 9.81*t²/2

dvs

9.81t² + 2*2.056*t - 2*4 = 9.81t² + 4.112t - 8 = 0

med lösningen

t = 0.7175 s (det finns även en ogiltig negativ lösning)

Rörelsen i horisontalled sker med konstant hastighet. När takpannan når marken efter 0.7175 s har den färdats sträckan

s = v_ht = 4.410*0.7175 = 3.16 m

Vi kollar resultatet med energiprincipen. Totala energin i förhållande till marken (före start):

mgh = m*9.81*(sin(25)*5+4) = 59.97m J

Totala hastigheten vid marken blir

V = sqrt(v_h² + v_v²) = sqrt(4.410² + 9.095²) = 10.108 m/s

E_kin + E_f = m(10.108²/2 + 8.89) = 59.98m J

vilket stämmer bra med ovanstående värde för den totala potentella energin.

Nyckelord: friktion [53]; lutande plan [15]; fallrörelse [31]; acceleration [6];

1 https://www.hb.se/PageFiles/204024/Naturvetenskap_160114.pdf
2 http://hyperphysics.phy-astr.gsu.edu/hbase/frict2.html#plo

Ursprunglig fråga:
Hur kan en Formel 1 bil dra fördel av luftmotståndet?
/alexander Å, IES Lund, Lund

Svar:
Kul fråga Alexander! Ja, en F1-bil är helt beroende av luftmotståndet! Utan det hade bilen kört av i den första kurvan!

Det man först tänker på är att luftens rörelse i förhållande till bilen ger en bromsande kraft (engelska drag), vilket naturligtvis inte är positivt. Det finns emellertid gott om effekt i motorn för att motverka motståndet. Avgörande för snabbheten hos F1-bil är inte motorstyrkan utan väggreppet.

Karossen på bilen designas för att minimera "drag" (som uppkommer genom turbulens) och för att maximera nedåtkraften (engelska downforce). Nedåtkraften skapas av en konstruktion som liknar en flygplansvinge (se fråga 12891 ) fast upp-och-ner.

Nedåtkraften adderas till tyngdkraften och utgör normalkraften. Friktionen, dvs väggreppet, är ju proportionellt mot normalkraften. Så större normalkraft ger bättre väggrepp vilket påverkar både acceleration, bromsförmåga och kurvtagning.

För att ytterligare öka "downforce" har F1-bilen vingar både fram och bak, se bilden nedan från Wikimedia. Man kan med en optimal kaross och vingar åstadkomma en "downforce" som överskrider tyngdkraften på bilen. Den skulle alltså teoretiskt kunna köras i taket!

De senaste åren har man infört en möjlighet att justera den bakre vingen under loppet. Detta kallas DRS (Drag Reduction System). När man vill köra om på en raksträcka kan man reducera "drag" och därmed få bättre acceleration. Man förlorar lite "downforce", så DRS deaktiveras automatiskt när man bromsar inför nästa kurva.

Se vidare Formula_One_car#Aerodynamics och Drag_reduction_system .

Nyckelord: friktion [53]; formel 1 [2]; flygplansvinge [8];

När en bil startar påverkar däcket vägen med en kontaktkraft riktad bakåt så att en motriktad friktionskraft uppstår som verkar på däcket framåt, det är den kraften som får bilen att rulla framåt. Motorkraften "omvandlas" till en framåtdrivande friktionskraft.

Om man sedan bromsar så vill däcken minska hastigheten, dvs kraften på vägbanan från däcken blir i rörelseriktningen och friktionskraften på däcket från vägen blir nu riktad bakåt. Men vad händer om vi har ett däck på ett lutande plan?

Kraften som vill få däcket att rulla ned är tyngdkraftens komposant längs med planet. Om man likställer den kraften med motorkraften hos en bil som startar så borde däcket påverka planet med en kraft uppåt längs planet och en friktionskraft uppstå mellan däck och plan som verkar på däcket nedåt längs med planet. Eller kan man inte tänka så? Jag har bortsett från rullmotstånd i exempelen ovan.
/Marilla A, Östra Gymnasiet, Skogås

Svar:
Friktion är ett ganska besvärligt begrepp eftersom det kan innefatta helt olika fenomen. Det vanigaste är "kloss på ett lutande plan", se fråga 16025 , Friktion och Friction .

Det du frågar om är statisk friktion (se fråga 14921 ) mellan däck och vägbana. Så länge däcket har grepp på vägbanan är friktionskraften lika med den framdrivande kraften F.

Skillnaden mellan plant läge och ett lutande plan är att tyngdkraften har en komponent parallellt med planet och att normalkraften reduceras, se figuren nedan. För att få bilen att köra uppför måste vi minst ha en kraft F från motorn som kompenserar för tyngdkraftens komponent parallellt med planet. Kraften F överförs alltså till underlaget genom den statiska friktionen mellan däck och underlag.

Nyckelord: friktion [53];

utsträckta armar med konstant fart. Hen önskar ”komma ikapp” en annan hoppare

under sig och drar därför in armarna till sidan för att minska på luftmotståndet.

Med armarna längs sidan är hans acceleration till en början 1,8 m/ s2 .

a) Hur stor är luftmotståndskraften när han har armarna utsträckta?

b) Hur stor är luftmotståndskraften när han precis har fört in armarna längst sidan?
/Linn S

Svar:
a När fallskärmshopparen nått sluhastigheten är jordens dragningskraft (m*g N) lika med luftmotståndskraften F.

F = mg = 80*10 = 800 N

b När hopparen drar in armarna minskar luftmotståndet men dragningskraften är den samma. Det är den resulterande kraften som ger accelelerationen 1.8 m/s².

(mg - F) = m*a

F = mg - ma = 80*10 - 80*1.8 = 656 N

Se även fråga 15385 .
/Peter E

Nyckelord: fallrörelse [31]; friktion [53];

Svar:
Om du menar hur stor rörelseenergi blocket får om man kan bortse från friktionen så blir kinetiska energin mgh. Den beror alltså bara av den vertikala höjden.

Om friktionen inte är försumbar kommer blocket ner med lägre energi - resten blir till värme. Om friktionen är stor och vinkeln liten fastnar blocket.
/Peter E

Nyckelord: lutande plan [15]; friktion [53];

Vi säger att jag har tyngden (70x10) = 700 N. Går jag upp för en 10 hög (och 5 meter lång trappa) har jag utfört arbetet W=700*10 = 7kJ

Om jag puttar en låda med kraften 50 N 3 meter har jag utfört arbetet = 50 x 3 = 150 J

Men om jag går helt vanligt (med min tyngdkraft 700 N) en sträcka på 10 meter, vilket arbete har jag ufört då? Och hur kan kan beräkna energin jag förbrukat?

För som jag förstått det utför man inget arbete om du inte puttar något? Samtidigt vet jag ju att det går åt energi för att gå en sträcka på 10 meter. Jag har ju tydligen inte utfört något arbete? Så vad har jag gjort? :) Detta är förvirrande för mig. Varför är det ett arbete om jag går upp för en trappa men inte om jag går på ex en fotbollsplan.

Vad är egentligen ett "arbete"?
/björn a, borås

Svar:
Jag tycker fråga 19235 och 13327 beskriver problemet ganska väl. Jag försöker göra det ännu tydligare då.

Vi utgår från definitionen på kraft, fråga 15131 , och arbete, fråga 13327 .

Om du förflyttar dig horisontellt utan förluster utförs inget nettoarbete. Förluster kan vara friktion då arbetet som går till att övervinna friktionen blir till värme. Om vi inte har någon friktion då? Jo, vi måste utföra ett arbete för att accelerera och få en rörelse i rätt riktning, dvs skapa rörelseenergi. Sedan måste vi stoppa vid målet. Detta kräver samma arbete som accelerationen, men formellt har detta negativt värde eftersom (broms)kraft och rörelseriktning är i motsatta riktningar. Om vi med 100% effektivitet kan återvinna rörelseenergin, så har vi nettoarbetet noll. Så arbetet du utför i praktiken är alltså för att kompensera för förlusterna - framför allt friktion och icke återvunnen rörelseenergi.

I fråga 13327 förklaras varför du blir trött av att hålla en väska med utsräckt hand trots att du inte utför något arbete.
/Peter E

Nyckelord: arbete [24]; kraft [12]; friktion [53];

1 http://hyperphysics.phy-astr.gsu.edu/hbase/work2.html

Svar:
Låt oss börja med att bortse från acceleration, uppbromsning och friktion. Eftersom vi då rör oss med konstant hastighet har vi ingen kraft och därmed inget arbete. Tar vi med friktionen behövs normalt samma kraft oberoende av hastigheten, vilket betyder samma arbete.

Tar vi sedan hänsyn till accelerationen så är det korrekt att det kostar mer arbete att accelerera till en högre hastighet, men samma arbete kan i princip återvinnas vid uppbromsningen. Detta är naturligtvis inte möjligt i praktiken, så förlusten vid acceleration/uppbromsning blir större vid högre hastighet.
/Peter E

Nyckelord: friktion [53];

Svar:
Om farten är v är rörelseenergin

W = mv²/2

Nettokraften på lådan är F. Arbetet som utförs på lådan om stoppsträckan är x är F*x, där F är konstant. Om vi sätter detta lika med W får vi

x = W/F

Återstår bara att räkna ut F. Denna består av två komposanter. Tyngdkraftens komposant a planets riktning är

mg*sin(a)

Friktionskraften räknas ut från normalkraften N som

m*N = m*cos(a)*mg

Nettokraften på lådan i rörelseriktningen blir då

F = mg*(sin(a) + m*cos(a))

Sträckan x blir då

x = (v²/(2g))/(sin(a) + m*cos(a))

vilket är i princip uttrycket du angett.
/Peter E

Nyckelord: friktion [53];

Svar:
Det finns ingen enkel formel för det. Mycket förenklat kan man betrakta problemet som friktion mellan fingrarna och den plana ytan. Om du känner friktionskoefficienten (vilket du knappast gör) kan du räkna ut den behövliga normalkraften, se fråga 14921 . Mer realistiskt är nog att mäta normalkraften med en liten platt våg som du fäster på vikten.
/Peter E

Nyckelord: friktion [53];

Om man då ökar hastigheten, varför glider föremålet av? Borde inte den resulterande kraften in mot centrum bara bli större då och hålla kvar föremålet?

Hur vet man vilken Max hastighet ett föremål klarar av?
/Maria O, Borgarskolan, Malmö

Svar:
Ja, friktionskraften accelererar föremålet in mot centrum så det kan beskriva en cirkelbana. Det är alltså den statiska friktionskraften (se fråga 17307 och 14921 ) som är centripetalkraften.

När den statiska friktionskraften blir mindre än den nödvändiga centripetalkraften rör sig föremålet utåt från centrum. Maximala friktionskraften bestäms av normalkraften som är konstant eftersom den beror av föremålets vikt.

Du kan bestämma den statiska friktionskoeffecienten enligt fråga 17307 . Annars får du helt enkelt mäta vid vilken hastighet föremålet börjar glida.

Observera att det finns ytterligare en friktionskraft riktad i rotationsriktningen eftersom du måste driva skivan så den inte stannar.
/Peter E

Nyckelord: friktion [53]; centripetalkraft [11];

Svar:
Nej, inte enligt den normala, enkla bilden av friktion. Friktionskoefficienten m är en materialkonstant som bara beror på egenskaperna hos de två ytorna som är i kontakt med varandra.

Friktionskraften beror emellertid av lutningen eftersom normalkraften N minskar med ökande lutning och friktionskraften F_f ges av

F_f = Nm

Se vidare fråga 16025 .
/Peter E

Nyckelord: friktionskoefficient [5]; friktion [53];

Svar:
Hej Malin! För att uppskatta friktionsförluster kan man beräkna den totala energin i en punkt på höjden h. Med traditionella beteckningar är (potentiell energi + rörelseenergi)

mgh + mv² = mgH (1)

där H är starthöjden.

För att kulan inte skall ramla ner i toppen av loopen måste centripetalaccelerationen minst vara lika med g, dvs

v²/r = r

dvs

mv²/2 = mgr/2

Den potentiella energin i toppen av loopen är mg*2r

Totala energin blir då

mg*2r + mgr/2 = mg(2.5r) (2)

där

2.5r = 27.5 cm --> r = 11 cm.

Startpunkten borde alltså ligga på höjden H = 2.5r. Detta är ju precis vad du räknat ut. Så varför stämmer det så dåligt med det experimentella värdet? Det kan vara både rullfriktion och luftmotstånd. Procenten friktionsenergiförluster med dina värden blir

(37-27.5)/37 = 26%

vilket verkar mycket. Detta är allt du kan räkna ut utan att göra hastighetsmätningar längs hela banan, eftersom (som du säger) friktionskoefficienten varierar längs banan.

Du har emellertid försummat kulans rotationsenergi. Av fråga 14738 framgår att rotationsenergin är 2/7 och translationsenergin 5/7. Vi måste alltså korrigera uttrycket (2) för rotationsenergin:

mg*2r + (mgr/2)*(7/5) = mg(2.7r) (3)

Detta ger det teoretiska värdet på starthöjden till

H = 2.7*11 = 29.7

och friktionsandelen

(37-29.7)/37 = 20%
/Peter E

Nyckelord: lutande plan [15]; potential/potentiell energi [30]; friktion [53];

Ex) Du lyckas dra ner en flytkropp med 100 N flytkraft och en volym på 5 dm2 till 10 meters djup, densitet vattnet:1,025 MT/m3. Där släpper du den. Går det nu att teoretiskt räkna ut hastigheten?
/Johan A, Rönnowskaskolan, Helsingborg

Svar:
Problemet är mycket likt fritt fall i luften, med skillnaden att vi även har en lyftkraft (Arkimedes princip, fråga 13509 ).

Nettokraften F blir tyngdkraften-lyftkraften. Observera att om densiteten hos föremålet är mindre än vattnets så blir nettokraften negativ och föremålet påverkas av en uppåtriktad kraft. Om föremålets densitet är större än vattnets blir nettokraften positiv och föremålet sjunker.

Sedan måste vi ta hänsyn till vattenmotståndet. Det är proportionellt mot hastigheten i kvadrat, se 15385 . Föremålet kommer relativt snabbt nå en sluthastighet när vattenmotståndet är lika med nettokraften F.

Som framgår av formeln i 15385 behöver du veta tvärsnittsytan hos kroppen, vattnets densitet (1000 kg/m³), nettokraften och kroppens form (konstanten C_d). Formeln för sluthastigheten V_t när man även tar hänsyn till lyftkraften blir alltså

V_t = sqrt(2*|F|/(r A C_d))
/Peter E

Nyckelord: friktion [53]; Arkimedes princip [32];

Svar:
Emma! Dämpning i amplitud hos en ytvåg är en ganska komplicerad process. Såvitt jag vet finns det inget enkelt uttryck, men dämpningen beror av bland annat vätskans viskositet (ger "friktion"), om det finns något på ytan (t.ex. olja, "gjuta olja på vågorna") och vattendjupet.

Det finns exempel på vågor för vilka amplituden ökar, t.ex. en tsunami som kommer in på grunt vatten (våglängden minskar varvid amplituden ökar).

Se även länk 1 och Mechanical_wave .
/Peter E

Nyckelord: friktion [53]; tsunami [5];

1 http://www.nyteknik.se/popular_teknik/kaianders/article221268.ece

Svar:
För att ljud skall utbreda sig i ett medium krävs massa (något som kan svänga) och elasticitet (en återställande kraft). Ljud som går genom ett material dämpas även genom en process som liknar friktion. Hur bra ljud leds i ett material beror av alla dessa faktorer. Ingen massa t.ex. är vakuum, och ljud leds inte i vakuum. Avsaknad av elasticitet eller hög dämpning ger dålig ljudutbredning, t.ex. sågspån.

För ljuddämpning i luft av olika temperatur se fråga 17383 .

För diskussion om ljudhastigheten i olika medier se fråga 4311 . Se även Sound_insulation#Absorption .
/Peter E

Nyckelord: ljudhastigheten [21]; friktion [53]; ljud [11];

Ursprunglig fråga:
1. Luftmotståndet på ett klot ges av formeln

F = k r²v² där

k = 0,92kg/m³
r - klotets radie
v - klotets hastighet

a) Kontrollera att enheterna stämmer i formeln

b) En bordtennisboll har radie 1,9 cm och massan 2,5 g. Bestäm sluthastighet för en bordtennisboll som faller genom luften.

b) skulle jag behöva hjälp med, mitt svar stämmer inte svaret med kollegans
/Azira H

Svar:
a (kg/m³)m²(m/s)² = kg*m/s² = N, vilket är SI enheten för kraft.

b Sluthastigheten uppnås när luftmotståndet är lika med tyngdkraften m*g:

m*g = k r²v²

v² = mg/(k r²) = 0.0025*9.81/(0.92*(0.019)²) = 73.8

v = sqrt(73.8) = 8.6 m/s

Låter lite mycket, men nog korrekt med de givna uppgifterna!

Låt oss kontrollera med uttrycket för sluthastighet som finns i fråga 15385 (med luftens densitet 1.2 kg/m³):

v = sqrt(2mg/(rAC_d)) = sqrt(2*0.0025*9.81/(1.2*p*(0.019)²*0.47)) = 8.8 m/s

vilket stämmer utmärkt med ovanstående värde!
/Peter E

Nyckelord: friktion [53]; luftmotstånd [11];

Några vänner och jag hamnade häromdagen i en rätt hätsk diskussion angående friktion, och hoppas att ni kanske kan hjälpa till att laga vår vänskap.

Ponera att man på något sätt kan bestryka en person med någon slags färg som gör att huden blir helt och hållet friktionsfri. Vad händer om denna person blir beskjuten?

Den teori som lades fram var att eftersom personen var helt friktionsfri så kan denne inte bli skadad av skottet eftersom det inte kan överföra sin rörelseenergi via friktionen. Stämmer detta? Är friktionen den enda länken till att överföra energi mellan kroppar?

Tack på förhand, Martin Paulsson
/Martin P, Norrköping

Svar:
Martin! Friktion är en kraft som är motriktad rörelseriktningen, se fråga 16025 . Det finns alltså ingen komposant av friktionskrakten riktad i sidled. Kulan går alltså rakt fram och bromsas upp lite grann av friktionen. Om man sätter på sig en rustning av metall kan kulan studsa mot metallytan, men det har inget med friktion att göra.
/Peter E

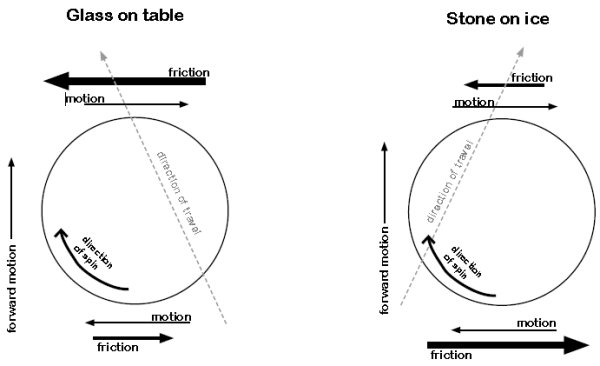
Nyckelord: friktion [53];

Förtydligande av frågan:

Om du drar en trådrulles tråd rakt upp (90 grader) kommer den att rulla ifrån dig, men om du drar den 180 grader kommer den att rulla till dig. Riktningen den rullar kommer att byta någonstans mellan dessa två vinklar och den vinkeln kan man räkna ut med en formel. Det är den formeln jag skulle vilja lära mig (Om kraft du drar den, radien, massan, bredden, eller något annat ändrar på gränsvinkeln)
/André R, Topeliusgymnasiet, Nykarleby

Svar:
André! OK, med tillägget blev frågan förståelig! Det är inte alls så enkelt som du framställer det. För det första så rullar trådrullen inte när du drar tråden horisontellt (180 grader). Trådrullen glider. Gränsvinkeln blir alltså beroende på en massa parametrar, bland annat friktionskoefficienten för rullning och friktionskoefficienten för glidning. I praktiken (jag har prövat det) har du även problem med att trådrullen vill rotera kring den vertikala axeln.
/Peter E

Nyckelord: friktion [53];

Svar:
Julia! Nej, det är tvärtom. Ditt uttryck där luftmotståndet är proportionellt mot v² är för höga hastigheter när man har turbulens, se Drag_(physics) . Då är mycket riktigt konstanten C ungefär 0.5 för en sfär. För låga hastigheter är luftmotståndet proportionellt mot v. För detta fall (Stoke's drag) har man en annan parametrisering för luftmotståndet och C förekommer inte.

Luftmotstånd är en ganska komplicerad process, så i de flesta fall löser man problem med enkla parametriseringar och mätningar, t.ex. i en vindtunnel.

Se även fråga 15385 .
/Peter E

Nyckelord: friktion [53]; luftmotstånd [11];

Svar:
Dämpning av ljudvågor är ett mycket komplext problem, se t.ex. länk 1. Med kalkylatorn i länk 2 kan man beräkna dämpningen av ljudvågorna vid de temperaturer du nämner:

-5^oC: 66.6 dB/km
-30^oC: 4.7 dB/km

Skillnaden i dämpning blir c:a 60 decibel dvs en faktor 10⁶ (se fråga 11847 hur man räknar med decibel). Detta är ju en enorm skillnad, men jag kan inte se att det är något fel i resonemanget, och andra sidor ger liknande resultat.

Det är dock relativt enkelt att förstå varför dämpningen ökar med ökande temperatur. Dämpningen beror på en växelverkan mellan ljudet (en ordnad rörelse som orsakar tryckförändringar) och den slumpmässiga rörelsen hos molekylerna relaterad till temperaturen. Den ordnade rörelsen hos ljudvågen övergår alltså i oordnad rörelse (värme) i en process som är analog med friktion. Länk 1 säger:

A sound wave in air has an attenuation factor due to a transfer of kinetic energy from the systematic mean molecular velocity of the wave, to random molecular motion (i.e. heat). This is analogous to frictional loss.

Nyckelord: friktion [53]; ljud [11];

1 http://www.silcom.com/~aludwig/Physics/Main/Wave_attenuation.htm
2 http://www.csgnetwork.com/atmossndabsorbcalc.html

Svar:
Eva!

Det finns flera olika friktionskoefficienter, t.ex. statisk friktion, glidfriktion (se fråga 14921 ) och rullfriktion.

Statisk friktion bestäms lätt med ett lutande plan, se Friction#Angle_of_friction .

Friktionskraften (figuren nedan) ges av

f = mN = mmg*cos(q)

Kraften riktad nedför planet är

mg*sin(q)

Om man långsamt ökar q kommer lådan att börja glida när de två ovanstående krafterna är lika, dvs

m = tan(q)

Du har tydligen en lösning för hur man bestämmer glidfriktion med ett lutande plan. Om man antar att friktionen är oberoende av hastigheten så kan man beräkna friktionskoefficienten mu från uppmätta glidsträckor på backen och den plana ytan:

maxhastigheten v = sqrt(2*s₁*g(sin(a)-mu*cos(a))) = sqrt(2*s₂*g*mu)

dvs

s₁(sin(a)-mu*cos(a)) = s₂*mu

Rullfriktion är emellertid mer komplicerat, se Rullmotstånd , Rolling_resistance och Kullager . Normalt är rullfriktionen för hårda material mycket liten, så approximationen utan friktion är tillräckligt bra, se fråga 14738 .

Nyckelord: friktion [53]; friktionskoefficient [5];

Svar:
Martin! Luftmotstånd är mycket komplicerat och det finns ingen exakt formel. Se fråga 15385 och Drag_(physics) för en approximativ formel. De flesta paramerarna i formeln är lätta att får fram. Densiteten för luft brukar tas till 1.2 kg/m³. 'Drag coefficient' C_d kan man hitta i Drag_coefficient . Där finns emellertid ingen form som liknar din fallskärm. I länk 1 finns emellertid ett värde för ett halvklot. Jag skulle tro att värdet för 'Hollow semi-sphere opposite stream' C_d=1.42 är ett rimligt värde du kan använda.

Lycka till med projektet!
/Peter E

Nyckelord: fallrörelse [31]; friktion [53];

1 http://www.engineeringtoolbox.com/drag-coefficient-d_627.html

Ursprunglig fråga:
Hej! Skulle vilja veta vad som händer när man "curlar" i curling? Vad är det som gör att stenen glider bättre då?
/Hannes H, Alströmergymnasiet, Alingsås

Svar:
Hannes! Intressant och aktuell fråga med tanke på lag Anette Norbergs insats i OS i Vancouver. Detaljerna för varför stenen "curlar" (avlänkas åt höger eller vänster i förhållande till den ursprungliga riktningen) är komplicerade och även kontroversiella. Vi behandlar detta i avsnittet mot slutet av svaret. Först en video om curling:

Vissa saker är man emellertid helt överens om:

1 Sopandet framför stenen skapar genom friktion värme som smälter isen och ger ett tunnt lager vatten. Detta minskar friktionen mellan stenen och isen.

2 Minskningen i friktion genom sopning medför dels att stenen går längre sträcka för en viss utgångshastighet och dels att den curlar (svänger) mindre.

3 Stenens curlande orsakas av friktionen mot isen och stenens rotation. Observera att man alltid sätter lite rotation på stenen: moturs om man vill att den curlar åt vänster och medurs om man vill ha en högerböj.

Till skillnad från andra sporter (t.ex. golf, bowling, skytte) kan man alltså påverka projektilens rörelse efter det att man släppt iväg den. Svårigheten är att man alltså får två effekter när man sopar: längre bana och mindre curl, och man måste besluta om en optimal kompromiss mellan effekterna.

SVTs kommentatorer vid OS-sändningarna från Vancouver spekulerade om vad resultatet skulle bli om det svenska damlaget skulle spela mot det svenska herrlaget. Man kom fram till att herrarna antagligen skulle vinna, men förklarade inte varför. Jag tror också herrarna skulle vinna helt enkelt för att de är tyngre och starkare, och kan på så sätt kontrollera stenen mer. Om man tittar på statistik för absoluta topp-curlare så har män c:a 90% och kvinnor c:a 80% lyckade stenar (slag).

Detaljerad förklaring till att stenen curlar

Låt oss börja med att göra ett enkelt experiment som du kan göra hemma. Ta ett köksglas (inte mormors finaste glas!) och leta upp ett jämnt, plant underlag, t.ex. en köksbänk. Vänd glaset upp-och-ner och skjut det längs bänken samtidigt som du sätter rotation på glaset, se vänstra bilden i nedanstående figur från Curling Science . Om du som i figuren roterar glaset medurs, så kommer glaset att avlänkas till vänster. Detta resultat är mycket förvånande för en curlare eftersom en curlingsten skulle avlänkas åt motsatt håll, se den högra bilden.

Varför reagerar glaset och curlingstenen olika på rotationen? Låt oss börja med att förklara varför glaset rör sig åt vänster. När glaset glider över bänken bromsas det up av en friktionskraft riktad rakt bakåt. Eftersom glasets tyngdpunkt ligger över bänkens plan, så kommer det att utsättas för ett vridmoment riktat bakåt. Trycket på framkanten av glaset blir då högre än trycket på bakkanten. Detta är samma effekt som att en bromsande bil får nosen nertryckt och en accelererande bil får nosen lyft. Eftersom glaset roterar får vi även en friktionskraft riktad åt vänster (friktionskraften är alltid motriktad rörelsen) i glasets framkant och en friktionskraft riktad åt höger i glasets bakkant. Eftersom normalkraften F_n enligt ovan är större i framkanten än i bakkanten blir friktionen större (se nedanstående formel), och vi kommer att få en nettokraft riktad åt vänster.

Varför uppför sig curlingsten annorlunda än glaset? För det första bör man veta att bottenytan på en curlingsten inte är plan, utan den har en skålformad fördjupning i mitten. Anläggningsytan mot isen är alltså en smal ring precis som för det upp-och-nervända glaset.

Skillnaden är att is smälter om den utsätts för högt tryck, se fasdiagrammet i fråga 12715 . Detta är skälet till att en kälke eller skridskor glider så bra på is - friktionen minskas genom ett tunnt vattenskikt. Precis som glaset utsätts stenen för en större normalkraft i framändan än i bakändan. I fallet curlingsten orsakar det högre trycket i framändan att friktionskoefficienten m minskar. Friktionskraften är ju

F = mF_n (1)

Eftersom minskningen i friktionskoefficienten är större än ökningen i normalkraften kommer friktionskraften att bli mindre i framändan. Stenen kommer då att i stället böjas av åt höger.

Eftersom förklaringen bygger på att en del is smälts, så bör det ha betydelse vilken temperatur isen har. Om isens temperatur är mycket låg borde man vänta sig att den har svårare att smälta och att friktionen skulle bli större. I länk 1 sägs det om Scotts (Robert_Falcon_Scott ) sydpolsexpedition:

Another key factor when considering the slipperiness of ice is temperature. Captain Scott noted during his Antarctic travels that once the temperature fell below -35 degrees C it become incredibly hard to pull sleds through the snow. This was because the heat produced by the friction between sled and snow was not enough to warm the ice to its melting point (0 degrees C) so no lubricating melt water was produced. Scott and his companions may as well have been pulling their sleds through sand. The closer the temperature of the ice is to its melting point the more melt lubricant is produced by sliding and the more slippery ice becomes.

I What Puts the Curl in a Curling Stone? finns ovanstående förklaring till curlande och referenser till fyra vetenskapliga artiklar från Canadian Journal of Physics om olika aspekter på curling. The motion of curling rocks: Experimental investigation and semi-phenomenological description är en senare artikel av samma författare. I den visas tydligt (men ganska svårgenomträngligt) att ovanstående modell är i stort sett korrekt även om vissa detaljer är oklara. Speciellt gäller detta hur stenen växelverkar med underlaget: växelverkar den med en fix isskiva eller med det rörliga vattnet under stenen? En annan effekt som är svår att förklara är att storleken av curl är i stort sett oberoende av stenens rotationshastighet. Intuitivt väntar man sig att en sten som roterar snabbare curlar mer.

I artikeln Comment on the motion of a curling rock framförs en annan modell där inte "våt friktion" (minskande friktionskoefficient) utan "torr friktion" (formel 1 ovan med konstant friktionskoefficient) används. Artikeln är emellertid inte av god kvalité, och slutsatserna är dubiösa.

Tester av modellerna

Det vore intressant att testa hur glaset uppför sig på is. Är det någon som har tillgång till mycket jämn is skulle jag vara tacksam om ni ville kummunicera era observationer till mig.

Ett annat experiment som är svårare att åstadkomma är att be ismakarna skruva upp kylningen till max. Skulle det gå att få ner temperaturen så mycket att man inte får någon smältning? Om det går skulle man få några mycket förvånade curlare: stenarna skulle bli mycket korta och curla åt fel håll !

Sopforskning

Sopandet är uppenbarligen en mycket viktig del av curling eftersom detta är lagets möjlighet att påverka stenens bana sedan den släppts. Curling, Olympic training and ice friction fundamentals är ett anslag till några forskare för att förbättra chanserna för det brittiska damlandslaget att försvara sitt guld från 2002 i Turin 2006. Tydligen räckte inte pengarna, för som känt så vann ju lag Norberg!

Vidare studier

Det finns som synes mycket i curling som är av fysikaliskt intresse, och då har vi inte tagit upp kollisioner mellan stenar och bevarandet av rörelsemängd och rörelseenergi.

För mer om curling se Wikipedia-artiklarna på engelska (Curling ) och på svenska (Curling ). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games . Länk 2 ger en alternativ förklaring.

Nyckelord: friktion [53]; *idrottsfysik [42];

1 http://www.research.ed.ac.uk/portal/en/projects/friction-on-icea-thermographic-analysis-of-surface-temperature(b3e37385-72c6-41bb-af3f-3440d39dcad2).html
2 http://www.forskning.se/nyheterfakta/nyheter/pressmeddelanden/curlingstenensexaktarorelserkartlagda.html

Ursprunglig fråga:
Jag skall hålla en utbildning för lastbilschaufförer. Hastigheten och förmågan att planera sin körning är alltid ett hett ämne som kräver konkreta svar.

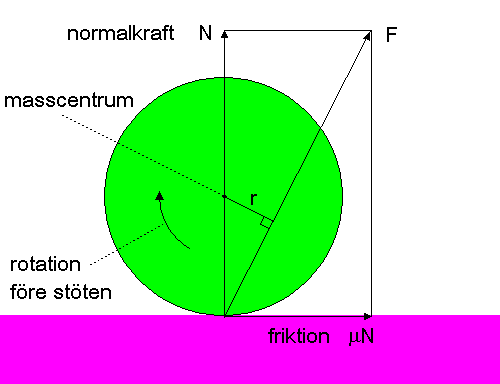
Fråga: Vad kostar det i energi (diesel) att öka hastigheten från 60 till 80 km/tim resp från 5 till 25/km/tim. Fordonets totalvikt 60 ton resp 20 ton. Konsekvens: Om man bromsar från 80 till 60 km/tim förlorar man i princip lika mycket i rörelseenergi som det kostat att accelera från 60 till 80 km/tim.
/Klas G, Brantevik

Svar:
Klas! Eftersom man normalt kör ganska långa sträckor så är det inte accelerationerna som är avgörande utan friktionsförluster - inklusive luftmotstånd. En personbil har en optimal hastighet på c:a 70-90 km/t, se länk 1 och 2 nedan. I länk 1 finns ett diagram på bränsleeffektivitet och tips för effektiv körning.

Om hastigheten är v så är luftmotståndet (bromsande kraften)

F_{luftmotstånd} = konstant*v²

(se Drag_(physics) ). Effekten går som F*v, så förlusterna från luftmotståndet går som v³. Å andra sidan kör man längre per tidsenhet, så slutresultatet blir att effektiviteten minskar som v².

Det är klart att det optimala är att köra med så konstant hastighet som möjligt. Om man inte har KERS (se fråga 16552 nedan) så är ju bromseffekten rena förluster.

Eftersom rörelseenergin är m*v²/2, kostar det mycket mer energi att accelerera från 60 km/t till 80 km/t än att accelerera från 5 km/t till 25 km/t. Kraften som krävs för accelerationen är (bortsett från luftmotståndet) densamma, men kraften verkar vid den högre hastigheten på en längre sträcka, så den erfordrade energin blir större.

Bränsleekonomi för en bil är ett ganska komplicerat ämne med många parametrar, så man kan inte räkna ut bränsleförbrukningen med hjälp av en enkel formel. Det bästa är att pröva själv - vissa bilar visar den ögonblickliga bränsleförbrukningen så för dessa är det enkelt.

Låt oss avslutningsvis beräkna hur mycket diesel det kostar att accelerera en 20 tons lastbil från 5 till 25 km/t och från 60 till 80 km/t. Energiutbytet för dieselolja är enligt Energy_content_of_biofuel 40.3 MJ/l. Om vi räknar med en effektivitet på 40% blir energiutbytet 16100 kJ/l. Detta värde har använts för att räkna ut förbrukningen i den sista kolumnen.

Hastighet     Ekin    DEkin   Förbrukning
  5    1.4     19.6
 25    6.9    476     456.4     0.028
.
 60   16.7   2790 
 80   22.2   4930    2140       0.13
km/t  m/s     kJ      kJ    liter dieselolja

Se även fråga 16552

Nyckelord: friktion [53]; rörelseenergi [14]; fossila bränslen [13]; luftmotstånd [11];

1 http://eartheasy.com/live_fuel_efficient_driving.htm
2 http://www.newton.dep.anl.gov/askasci/eng99/eng99540.htm

Ursprunglig fråga:
Hur omvandlas bilens bränsle till rörelseenergi och kan man ta vara på värmeenergin som bildas vid inbromsning och i så fall används den metoden idag? Hur fungerar bromsar och styrsystem, med och utan servo?
/Alida F, Uppgårdskolan, Stenhamar

Svar:
Alida! Det är mycket omfattande frågor du ställer och de är delvis mer teknologi än fysik. Jag kommer att behandla några av de fysikaliska aspekterna i din fråga.

Förbränningsmotorer

Bilens bränsle förbränns tillsammans med syre från luften i en cylinder. Varm gas tar mer plats än kall gas och expansionen driver en kolv. Via en vevaxel omvandlar man fram-och-tillbaka rörelsen till rotation som kan driva hjulen, se nedanstående animering från Wikimedia Commons (Engine ). Observera att det är inte den höga temperaturen i sig som driver förbränningsmotorn utan skillnaden i temperatur mellan de varma och kalla delarna. En förbränningsmotor måste alltså alltid kylas - oftast med vatten. I ett kraftverk eller fabrik kan man använda kylvattnet för uppvärmning, men i en bil är det varma kylvattnet en ren energiförlust. Effektiviteten (verkningsgraden) för en förbränningsmotor (producerat mekaniskt arbete/(bränslets energiutveckling) är av storleksordningen 40% (Internal_combustion_engine ).

Bromsar

Den traditionella konstruktionen för bromsar är två plattor eller cylindrar som bringas i kontakt och genom friktion förvandlar mekanisk energi till värme. Normalt är denna värme en ren förlust.

Det finns emellertid bromsar som återanvänder bromsenergin.

Om bilen drivs av en elmotor och batterier kan man använda motorn som broms. Elmotorn blir i stället en generator som producerar ström som laddar patterierna. Det är alltså det mekaniska motståndet från generatorn (Lenz's_law ) som ger bromsverkan. En stor del av energin kommer till nytta från det uppladdade batteriet. Se Regenerative_brake#The_motor_as_a_generator .

En annan lösning är att använda sig av ett svänghjul. Ett svänghjul (se Flywheel ) är en mekanisk anordning vars syfte är att lagra rörelseenergi genom att en tung cylinder sätts i rotation. För ett fordon överför man rörelseenergi till rotationsenergi hos svänghjulet. Denna rotationsenergi kan sedan återanvändas för acceleration. Systemet används bland annat av några stall i Formel 1. Systemet kallas KERS (Regenerative_brake#Kinetic_Energy_Recovery_Systems ). Man kan med detta system få några extra hästkrafter för en snabb omkörning. Svänghjulet laddas alltså upp av uppbromsningarna. Anledningen till att inte alla Formel 1 stall använder KERS är att systemet är ganska tungt (c:a 25 kg) och därför medför begränsningar i den optimala viktfördelningen i bilen. (Kommentar: Systemet var förbjudet under säsongen 2010, men är tillåtet från säsongen 2011.)

Hydraulik/servosystem

Hydraulik är ett system med två kolvar med olika diameter som är förbundna med en slang innehållande en vätska, vanligen olja. Vätskan är inkompressibel (kan inte tryckas ihop), och man skapar ett övertryck genom att trampa på en pedal. Om kolvarnas ytor förhåller sig som 1/10 får man en förstärkning av kraften med en faktor 10. På samma sätt som för en hävstång betalar man kraftförstärkningen med att den mindre kraften verkar över en längre sträcka, se Hydraulik .

Ett servo-system skall enligt en strikt definition (Servomechanism ) även innehålla en extern drivkälla (t.ex. vakuum från motorn) och återkoppling.

Nyckelord: hävstång [5]; friktion [53]; verkningsgrad [26]; energilagringssystem [7]; formel 1 [2];

Ursprunglig fråga:
Varför snurrar en boll åt andra hållet efter att den studsat i golvet? Alltså om du skruvar den åt höger kommer den efter studsen att snurra åt vänster. Vi har provat flera gånger och det blir lika dant. Vår lärare kunde inte förklara varför men tipsade oss att skriva hit och fråga.
/kerstin ö, kilafors skola, kilafors

Svar:
Kerstin! Det beror på bollens och golvets egenskaper om snurr-riktningen ändras. Om friktionen boll-golv är stor kan rotationsriktningen säkert ändras.

Se nedanstående figur. Bollen roterar på nervägen medurs. Vi har en normalkraft vinkelrätt mot golvet och en friktionskraft parallellt med golvet och motriktad rotationen. Vi kallar resultanten till dessa två krafter för F. Eftersom F inte går genom masscentrum skapar F ett rotationsmoment F*r. Detta är motriktat den urspungliga rotationen. Om rotationsmomentet är tillräckligt stort (dvs friktionen är tillräckligt stor) kommer det att orsaka att bollens rotation vänder.

Detta är en mycket idealiserad bild - i verkligheten måste man ta hänsyn till att bollen deformeras och att en del av rörelseenergin av inre friktion förvandlas till värme.

Nyckelord: skruvad boll [10]; friktion [53];

Ursprunglig fråga:
Vad menas med friktion och när är den är bra eller dålig ?
/Matilda L, sofiedalskolan, gävle

Svar:
Matilda! Nationalencyklopedin definierar friktion som

"motstånd mot glidning mellan två föremål i kontakt. Friktionskraften är riktad motsatt glidningen, normalt lika med friktionskoefficienten gånger den sammanpressande kraften mellan föremålen och oberoende av kontaktytans storlek och av glidfarten. Friktion orsakas av kraftverkan mellan atomer i ytskikten hos föremålen och studeras inom tribologi. Friktion är till nytta (minskar halka, t.ex. mellan bildäck och vägbana), men medför förluster i tillgänglig energi när högvärdig rörelseenergi omvandlas till värme (friktionsförluster)."

Wikipedia säger:

Friktion eller gnidningsmotstånd har att göra med hur ytan på materialet är beskaffad. En slät och jämn yta som på is ger mindre friktion än en skrovlig och knottrig yta som på betong. Det beror helt enkelt på att utsprång på den ena kroppen tar i fördjupningar på den andra, så att det behövs extra kraft för att få dem loss igen. De elektromagnetiska krafterna mellan atomer spelar emellertid också en betydande roll. När två kroppar är i nära kontakt håller atomerna fast vid varandra och verkar då i motsatt riktning mot rörelsen. På så sätt omvandlas kinetisk energi (rörelseenergi) till värme. (Friktion )

Om friktion är bra eller dålig? Jag antar du menar om vi har nytta av den eller tvärtom. Om inte friktionen funnits hade du inte kunnat gå, du hade ramlat omkull hela tiden. Å andra sidan hade bilar dragit mindre bensin - men inte kommit någonstans! Så det är nog väl att friktion finns !

Man kan efter behov öka friktionen - för bilar med dubbdäck och sandning av vägar - eller minska friktionen - med olja i en bilmotor. Dessa åtgärder ändrar friktionskoefficienten. Man kan även öka friktionen genom att öka normalkraften, t.ex. med vingar eller spoilers på en formel 1 bil (downforce).

Se fler frågor om friktion under nedanstående länk. Se även Friktion och Friction . Se fråga 14921 för begreppet friktionskoefficient.

Nyckelord: friktion [53]; friktionskoefficient [5];

Svar:
Patrik! Jag har pratat med en tävlingscyklist om detta och han påpekar att rullfriktionen för en tävlingscykel är helt försumbar i jämförelse med den dominerande effekten: luftmotståndet. Alla eventuella effekter på rullfriktionen från hjulens storlek är försumbara jämfört med höjdens påverkan på luftmotståndet. En ytterligare begränsning är att hjulen enligt reglerna måste vara lika stora bak och fram.

Den optimala storleken på hjulen beror på kroppsstorleken. Det är uppenbart att med stora hjul kommer man med normal design högt upp och orsakar stort luftmotstånd. Detta blir mindre med små hjul (cykel/cyklist-paketet mer kompakt). För lagtempo är lite mindre hjul optimalt eftersom man då kan komma närmre varandra. Man kan emellertid inte ha hur små hjul som helst: det måste finnas plats för pedalerna och ett visst avstånd mellan kroppen och pedalerna så man kan få kraft i trampandet. Små hjul är dessutom känsligare för ojämnheter i vägbanan.

Jag tror att dessa avvägningar i stort sett definierat hjulstorleken till 559 mm för mountainbike och 622 mm för en vanlig tävlingscykel. Att avvika från detta är svårt framför att för att det är svårt att få tag på hjul och däck i andra storlekar.
/Peter E

Nyckelord: friktion [53]; *idrottsfysik [42];

Svar:
För att lösa ett sådant här problem måste du betrakta alla krafter som påverkar bilarna:

tyngdkraften - proportionell mot massan
luftmotståndet - en funktion av hastigheten
friktionen - proportionell mot normalkraften som är proportionell mot massan

Accelerationen a ges av F = m*a, så större massa ger lägre acceleration vid samma kraft.

Toppfarten då? Eftersom friktionen är större för den tyngre bilen blir nettokraften framåt mindre för den tyngre bilen, och topphastigheten lägre.

Vilken bil rullar längst på tomgång från samma fart? Detta är omöjligt att besvara generellt. För det första är friktionen för ett fordon mer komplicerad. Förutom "vanlig" friktion som är proportionell mot normalkraften har vi vad vi skulle kunna kalla rullfriktion, alltså de rörliga delarnas bromsverkan. Denna behöver inte nödvändigtvis skala sig som massan. Man har också "däcksfriktion" - det går åt energi för att väma upp däcken genom att de deformeras.

Vilken bil som rullar längst beror på den relativa styrkan på de uppbromsande krafterna. Om den "vanliga" friktionen dominerar så rullar bilarna lika långt (F=ma=friktionskoefficient*mg, dvs a är oberoende av m). Om friktionen är liten så att luftmotståndet dominerar kommer den tyngre bilen att rulla längre eftersom den bromsande kraften F(v) inte beror av massan medan uppbromsningen a beror av massan:

F(v) = m*a

dvs a blir mindre för större massa.
/Peter E

Nyckelord: friktion [53];

Svar:
Nej, om man tar hänsyn till luftmotståndet (Drag_(physics) ) kommer dom inte att landa samtidigt! Luftmotståndet är proportionellt mot tvärsnittsarean och mot hastigheten i kvadrat (v²). Kloten faller alltså snabbare och snabbare, men eftersom luftmotståndet ökar med hastigheten kommer man till en punkt då accelerationen upphör, dvs att klotet faller med en konstant hastighet. Detta sker när luftmotståndet är lika med tyngdkraften. Tyngdkraften, som accelererar klotet, är proportionell mot massan (F = m*g). Om kloten är lika stora (dvs har samma tvärsnittsarea) får vi om vi sätter F = luftmotståndet:

m*g = konstant*v²

Sluthastigheten (gränshastigheten) v_s ges alltså av

v_s = konstant* sqrt(m)

Detta betyder t.ex. för ditt exempel att sluthastigheten för det tyngre klotet är sqrt(2)=1.4 gånger större än sluthastigheten för det mindre.

Ovanstående betyder att falltiden för det lättare klotet är 1.4 gånger större än falltiden för det tyngre. Vi har då borsett från accelerationsfasen vilket vi kan göra om kloten släpps från hög höjd.

För övrigt är det olämpligt att släppa bowlingklot från flygplan, så vi antar det hela är ett tankeexperiment .

Se vidare Free_fall och (mindre omfattande men på svenska) Fritt_fall . För att ge en känsla av vilka hastigheter det rör som om kan man säga att sluthastigheten för en fritt fallande människa är c:a 200 km/t. Sluthastigheten för andra former kan beräknas med formeln i Terminal_velocity#Examples , se nedanstående bild. 'Drag coefficient' som förekommer i formeln är uppskattad i Drag_coefficient .

Uppskattning av fallhastigheten för en människa:

Det är ganska stor osäkerhet för ett så oregelbundet objekt. Detta bör dock inte vara alltför långt från verkligheten:

v_t = sqrt(2*80*10/(1.2*0.5*1)) = 52 m/s = 52*3.6 = 185 km/t

som är nära ovanstående empiriska värde på 200 km/t. ______________________________________________________________________

I Wikipedia artikeln Drag_equation ges en kvalitativ motivering för att luftmotståndet skall vara proportionellt mot hastigheten i kvadrat:

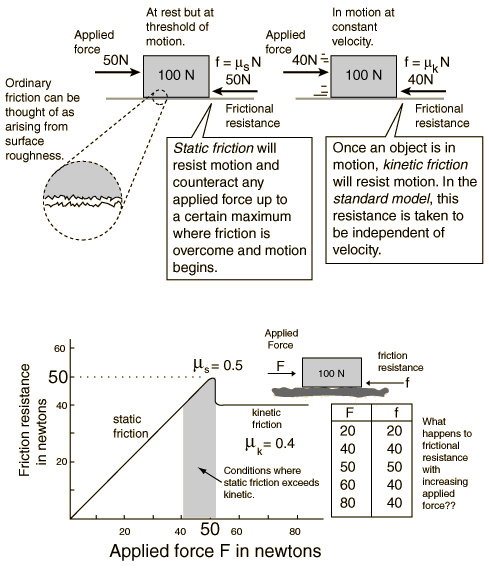
"Of particular importance is the v² dependence on velocity, meaning that fluid drag increases with the square of velocity. When velocity is doubled, for example, not only does the fluid strike with twice the velocity, but twice the mass of fluid strikes per second. Therefore the change of momentum per second is multiplied by four. Force is equivalent to the change of momentum divided by time. This is in contrast with solid-on-solid friction, which generally has very little velocity dependence."

Nyckelord: friktion [53]; fallrörelse [31]; luftmotstånd [11]; gränshastighet [4];

Svar:
Du utför ett arbete när du sträcker gummisnodden. En del av detta arbetet omvandlas genom friktion i gummisnodden till värmeenergi. Fenomenet är helt analogt med att putta runt en kloss på ett skrovligt underlag. Klossen blir varm av friktionen.

En del av energin i ett deformerat elastiskt föremål lagras som potentiell energi i vad som kan kallas elastisk energi: den potentiella energi som "upplagras" i ett elastiskt material som utsätts för deformation, till exempel för ett utsträckt gummiband eller hos en spiralfjäder som trycks samman eller dras ut. (Elastisk_energi )

Se även diskussionsforum, länk 1.
/Peter E

Nyckelord: friktion [53]; elasticitet [4];

1 http://fragelada.fysik.org/forum/display_message.asp?mid=663

Ursprunglig fråga:
Fick en förfrågan om friktionskraften är areaberoende. Känns som att det borde vara så att större area ger större friktion. Fast om jag kollar på formeln friktionskraften = friktionskoefficienten*normalkraften finns inget som visar på att friktionskraften skulle vara areaberoende. Är friktionskraften areaberoende? Hur förklarar man det? Hur förklarar man att vilofriktionen är större än glidfriktionen?
/Marianne A, Ehrensvärdska gymnasiet, Karlskrona

Svar:
Marianne! Friktionskraften är ett mycket komplicerat fenomen när man djupdyker i det, men standardmodellen är mycket enkel: friktionskraften f är proportionell mot normalkraften N:

f = mN

där proportionalitetskonstanten m kallas friktionskoefficient. Som du ser är det inget beroende av arean. Att det är så kan man intuitivt förstå eftersom om vi t.ex. dubblar arean så blir normalkraften per ytenhet hälften så stor, så resultatet blir oförändrat. Proportionaliteten mellan friktionskraften och normalkraften kan man förstå om man tänker på att den reella kontaktytan (utgörs av några atomer som sticker ut) är ganska liten. Om man ökar normalkraften så kommer atomerna att flytta sig lite, och fler atomer kommer i kontakt med varandra. Detta gör att friktionen ökar. Att den ökar linjärt kan enklast betraktas som ett experimentellt faktum.

Bilderna nedan (från Hyperphysics, länk 1) visar vilofriktion (statisk) och glidfriktion (kinetisk). Den förra är som du säger större. Anledningen är komplex och beror av materialet, men det har att göra med att knöligheter fastnar i varandra när klossen ligger still, medan denna effekt minskar om klossen rör sig.

I den nedre figuren visas friktionskraften f som funktion av den drivande kraften F. Klossen väger 10 kg, så normalkraften är hela tiden c:a 100 N. Till vänster (i origo) är friktionskoefficienten noll (ingen drivande kraft att motverka). Friktionskoefficienten ökar när man går åt höger tills den blir 0.5. Då övervinns friktionskraften och klossen börjar röra sig. Observera att så snart klossen sätts i rörelse så minskar friktionskoefficienten till (i det här exemplet) 0.4.

Se vidare länk 1 och friction för mer om friktion än du någonsin vill veta .

Nyckelord: friktion [53]; *vardagsfysik [64]; friktionskoefficient [5];

1 http://hyperphysics.phy-astr.gsu.edu/hbase/frict.html

Ursprunglig fråga:
Varför kastar man en golfboll längre än vad man kastar en pingisboll?
/Beatrice N, Nya läroverket, Luleå

Svar:
Beatrice! Eftersom en golfboll och en pingisboll är ganska exakt lika stora och har samma form, så är det ganska lätt att förklara. Om vi antar att att utgångshastigheten är lika, så är kraften som orsakas av luftmotståndet lika. En lätt boll (pingisboll) påverkas mer av denna kraft än en tyngre boll (golfboll), vilket innebär att den lättare bollen bromsas snabbare än den tyngre.

För den som vill ha formler gäller att

F = ma

och alltså om kraften F är konstant minskar accelerationen (uppbromsningen) när massan ökar.

Luftmotståndet är för för höga hastigheter proportionellt mot hastigheten i kvadrat (v²) och för lägre hastigheter proportionellt mot hastigheten (v). Länk 1 är en avancerad artikel på engelska.
/Peter E

Nyckelord: friktion [53];

1 http://en.wikipedia.org/wiki/Air_resistance

Svar:
För att förstå detta använder vi oss av en förenklad fysikalisk modell . Vi antar att sandkornet för enkelhets skull är sfäriskt med radien r och densiteten r.

Vindpåverkan V är proportionell mot tvärsnittsarean dvs

V = konst*p r².

Tyngdkraften T är proportionell mot massan dvs

T = m*g = (4p r³/3)*r*g.

Förhållandet T/V blir då

(4p r³/3)*r*g/(konst*p r²) = C*r

där C är en (ännu) obestämd konstant. Förhållandet är alltså proportionellt mot r, dvs ju större sandkornet är, desto mer dominerar tyngdkraften. När sandkornet blir riktigt stort (en sten) är T mycket större än V, varför vi får en resulterade kraft nästan rakt ner. Stenen påverkas alltså mycket lite av vinden.

Vi kan nu kontrollera om modellen är bra och i så fall bestämma konstanten C genom att göra mätningar i en konstant vind med sandkorn/stenar av olika storlek. Vi mäter avvikelsen från lodlinjen och plottar detta som funktion av radien r. Om resultatet blir en någotsånär rät linje kan vi bestämma C.

Konstanten C kommer antagligen att vara proportionell mot vindhastigheten i kvadrat. Genom att genomföra mätningar vid olika vindhastighet skulle man kunna verifiera detta samband.

I praktiken skulle det ovan beskrivna experimentet antagligen fungera mycket dåligt - vinden är i verkligheten aldrig konstant. Man skulle kunna förbättra försöket genom att utföra det inomhus med en stark fläkt. Om man i stället för fallande sandkorn använde sig av olika stora kulor av samma material som är upphängda i en tråd och mätte avvikelsen från lodlinjen, skulle man antagligen få ett bättre resultat.

Se även svaren om störloppsåkaren och bobåkarna: bobåkning/störtlopp .
/Peter E

Nyckelord: fysikalisk modell [12]; friktion [53];

Ursprunglig fråga:
I ett laboration som vi gjorde i skolan, vi skulle visa att Kraftekvationen gäller där vi använde tyngden av massan m för att sätta fart på vagnen med massan M. Med hjälp av två ljusportar bestämde vi vagnens hastigheter vid två tillfällen. Sedan bestämde vi värden på den accelererande kraften (dragkraften) samt produkten av massan och accelerationen. Vi fick då olika värden på kraften och produkten av massa och accelerationen. Min fråga är att vilket är förklaringen till avvikelsen mellan värden på kraften och produkten av massan och accelerationen??? Och hur kan man redovisa för de korrigeringar som bör göras??
/Sara H, Birgitta, Linköping

Svar:
Hej Sara!

Ni har gjort ett experiment för att undersöka tröghetslagen F=ma, Newtons andra rörelselag. Med de givna förutsättningarna väntar man sig idealiskt följande samband:

F = mg = (m+M)a

där mg är den accelererande kraften och m+M är massan som accelereras.

För det första är alla mätningar behäftade med osäkerheter (i bland oegentligt kallade fel). För försöket ni gjort kommer det sedan säkert in en systematisk felkälla: friktionen. Om ni kan mäta denna på ett oberoende sätt skulle ni kunna korrigera för den.

Möjligen skulle man till en del kunna få en uppfattning om friktionen genom att variera tyngden m. I en första approximation beror friktionen av M (proportionell mot normalkraften), och bör alltså bli av relativt mindre betydelse om m (och därmed kraften) ökas.

På min begäran skickade du följande mätdata (presentationen något modifierad):

  m (kg)      M (kg)      a (m/s2)    M/m
  0.04        0.353       1.01        8.83
  0.05        0.353       1.13        7.06
  0.02        0.353       0.468       17.7
  0.02        0.516       0.332       25.8
  0.02        0.580       0.224       29.0
  0.03        0.353       0.693       11.8
  0.03        0.522       0.481       17.4

a = g/(1+M/m)

Tar vi hänsyn till en friktionskraft f*M*g får vi

a = (g-f*M*g/m)/(1+M/m)

Detta samband är plottat i nedanstående figur för f=0.5 och 1%. Dina uppmätta data uppvisar lite spridning, men jag tycker att de stämmer relativt bra med kurvan för f=0.5%. Olika värden på M har markerats med olika symboler, men jag kan inte se någon systematik.

För att förbättra experimentet skulle man kunna ta fler mätpunkter för att få en bättre uppfattning om de tillfälliga mätfelen i bestämningen av accelerationen.

Nyckelord: Newtons rörelselagar [21]; friktion [53];

Är det inte så att det optimala är att, behålla sin fart genom att ha så lite luftmotstånd och friktion som möjligt. Det är väl ingen nackdel om du "hoppar" flyger ibland, särskilt om du inte ökat luftmotståndet och förhoppningsvis kortat av sträckan. Kan du hjälpa mig reda ut begreppen flyga, glida osv.
/Kenth L, Jakobsberg, Järfälla

Svar:
Med din begränsning är det korrekt att det går snabbare att flyga. Anledningen till att det i allmänhet anses gå långsammare om man flyger långt är nog dels att det är svårare att styra kroppen så att man har minimalt luftmotstånd om man flyger fritt i luften och dels att sträckan kan bli längre eftersom flyktbanan inte är en rät linje utan en parabelliknande kurva. Så hur bra eller dåligt det är att flyga beror på hur skicklig man är att minimera luftmotståndet i luften, och hur markprofilen ser ut, dvs vilken väg är den kortaste. Lägg märke till att de flesta störtloppsåkare reser sig upp och sträcker ut armarna för att hålla balansen när de hoppar. Se även nedanstående fråga.
/Peter E

Se även fråga 869

Nyckelord: friktion [53]; bobåkning/störtlopp [4]; *idrottsfysik [42];

Svar:
Hm, intressant fråga som jag aldrig tänkt på. Ja, det har med atomernas rörlighet att göra.

Allmänt kan man säga att föremåls förmåga att häfta i varandra (friktion) bland annat beror av ytornas skrovlighet. Skrovliga ytor (sandpapper mot sandpapper) har hög friktion och blanka (metall mot metall) har låg friktion. Om emellertid två metallytor är mycket jämna, så kommer atomerna så nära varandra att man kan få hög friktion.

Både fast och smält smör har klibbighet - pröva med ett finger - så skillnaden ligger inte där. Skillnaden är att i fast smör kan molekylerna inte lätt röra sig i förhållande till varandra, medan dom i smält smör rör sig ganska fritt.

Låt oss göra följande experiment: lägg en kall potatis på en tallrik (så vi inte kladdar!). Sätt en liten klick smör på potatisen. Du bör nu ganska lätt kunna fästa en annan kall potatis vid smörklicken. Vi konstaterar att kallt smör har klisterförmåga.

Upprepa sedan försöket med varma potatisar. Vad händer? Jag tror (hoppas?) att den övre potatisen glider ner på tallriken. Smält smör är alltså ett dåligt klister.

Vad som händer är att smörlagret mellan de varma potatisarna smälter, och smörmolekylerna kan röra sig i förhållande till varandra - potatisen glider ner. Det är t.o.m. så att smält smör har sämre klisterförmåga än inget smör alls. Du kan säkert ganska lätt lägga en potatis på en annan utan smör. Smält smör fungerar alltså som ett glidmedel, som hindrar potatismolekylerna att komma i kontakt (detta kallar vi friktion) så fallet kan stoppas.
/Peter E

Nyckelord: friktion [53];

Ursprunglig fråga:
Jo jag undrar varför man har bredare däck vid fartsporter som t.ex. formel 1? Jag förstår att det har med väghållningen att göra men jag tycker att det borde bli en kortare bromssträcka om du har breda däck än om du har ett par smala däck som utsätts för samma normalkraft och är tillverkade i samma meterial. Stämmer inte det?

Ett annat ex. kan ju vara vem som har kortast startsträcka om förutsättningen är att det inte får spinna loss någon gång.
/Arvid M, ABB Industrigymnaium, Västerås

Svar:
Enligt den förenklade teorin för friktion som presenteras i skolfysiken så beror inte friktionskraftens storlek på kontaktytans area utan endast på normalkraftens storlek. I praktiken är det däremot så att friktionskraften ökar med arean. Breda däck ger större friktionskraft och bättre väghållning. Med dubbar blir effekten ännu större eftersom ett bredare däck hat plats för fler dubbar.

Dessutom förkortas bromssträckan och accelerationen blir bättre. Friktionstalet för kontakt gummi - asfalt är ca 1,5 för bra gummiblandningar och varma däck.

Friktionen mot asfalt är, kanske lite förvånande, större om man har omönstrade däck än om man har mönstrade. Anledningen till att däck på vanliga bilar är mönstrade är framför allt för att eventuellt vatten skall komma undan. Tänk på formel-1 bilar: vid torrt väder använder man omönstrade däck, men om det börjar regna måste man omedelbart byta annars kommer bilarna att vattenplana av banan.

Fundera: Varför har man vingar på formel 1-bilar?

Fundera: Hur fort kan man köra genom en kurva med en radie på 100 m? Antag att normalkraften är lika stor som tyngdkraften.
/GO

Nyckelord: friktion [53]; *idrottsfysik [42];

Ursprunglig fråga:
I slalomsammanhang får man av s.k. experter höra: "Det är bra att du har lagt på dej några extra kilon, för då går det ju fortare." I praktiken tycks det vara så. Men energiprincipen säger ju att massan är oväsentlig (under förutsättning att vi endast har Wp och Wk som växelverkar). Den enda förklaring jag har till fenomenet har att göra med Newtons första princip - en tröghetsfråga alltså. Den tyngre alpinisten besitter ju en större rörelsemängd. Har du några förklaringar?
/Staffan L, Tekniskt/Naturvet. Basår, Skellefteå

Svar:
Detta påstås ofta av kommentatorer, men ligger det något i det?

Det mest väsentliga (förutom skicklighet att åka skidor) är luftmotståndet (friktion). Det är i princip luftmotståndet som bestämmer hastigheten. Vad händer då med en skidåkare som lägger på hullet? Jo han eller hon blir lite större och lite tyngre. Men eftersom volymen av en ideal klotformig skidåkare går som r³ medan ytan går som r², så ökar massan (volymen) snabbare än ytan med faktorn r. Kraften som drar skidåkaren nedåt är ju proportionell mot massan, medan kraften som bromsar (luftmotståndet) är proportionell mot ytan. Vi får allstå en större kraft för den tyngre skidåkaren, medan luftmotståndet inte ökar lika mycket. Så om allt annat är lika så har en tyngre åkare en fördel.

Vad gäller glidfriktion mellan snön och skidorna är den propotionell mot normalkraften som är proportionell mot massan. För denna har alltså skidåkarens vikt ingen betydelse eftersom både friktionen och den dragande kraften är proportionell mot massan.

Se även fråga 20012 .
/PE

Nyckelord: friktion [53]; bobåkning/störtlopp [4]; *idrottsfysik [42]; luftmotstånd [11];

1 http://www.nbclearn.com/portal/site/learn/resources

Ämnesområde	BlandatElektricitet-MagnetismEnergiKraft-RörelseLjud-Ljus-VågorMateriens innersta-Atomer-KärnorPartiklarUniversum-Solen-PlaneternaVärme
Sök efter
Grundskolan eller gymnasiet?	FörskolaGrundskolaGymnasiumLärarutbildning
Nyckelord:	#ljus [63]*astronomi/astrofysik och rymdfart [2]*biologi [20]*fysikaliska definitioner [1]*fysiologi [13]*geologi [16]*idrottsfysik [42]*kemi [22]*meteorologi [20]*miljöpåverkan [14]*nöjesparksfysik [12]*vardagsfysik [64]*verktyg [15]3d-bilder [6]aberration [1]absoluta nollpunkten [9]acceleration [6]accelerator [7]addition av hastigheter [2]aerosol [4]akustik [6]alfasönderfall [7]annihilation [14]antimateria [16]arbete [24]Arkimedes princip [32]asteroid [10]astrobiologi [9]astrologi [5]atomradie [8]Avogadros tal [3]ballong [25]bandgenerator [3]barometerformeln [1]batteri [25]belysning [6]bernoullieffekten [6]betasönderfall [15]big bang [37]bildskärmar [4]bindningsenergi [23]blixt [18]blå himmel [12]bobåkning/störtlopp [4]Bohrs atommodell [9]Bose-Einstein-kondensat [6]brandvarnare [2]bränslecell [3]centrifugalkraft [15]centripetalkraft [11]comptonspridning [3]corioliskraft [7]dagens längd [3]daggpunkten [2]dagjämning [6]Darwins evolutionsteori [8]de Broglie våglängd [1]decibel [11]delton [2]diffraktion [4]diffusion [1]dimensionsanalys [7]dimkammare [2]dopplereffekt (ljud) [3]dopplereffekt (ljus) [3]drickande fågeln [1]dubbelspalt [4]duschdraperi [2]Einstein, Albert [1]eko [3]elasticitet [4]elastisk stöt [12]elektrisk krets [7]elektrisk ström, hastighet [4]elektrisk ström, skada [6]elektromagnetisk strålning [21]elektronskal [12]elektrostatik [4]elsäkerhet [18]energikällor [26]energilagringssystem [7]enkelspalt [1]entropi [7]EPR, Bell, Aspect [3]evighetsmaskin [14]exoplaneter [17]fallrörelse [31]faradaybur [10]fasdiagram [7]felberäkning [6]Fermats princip [1]ferromagnetism [9]fiberoptik [4]fission [15]fluorescens [6]flygplansvinge [8]flykthastighet [4]formel 1 [2]forskningskarriär [1]fossila bränslen [13]fotoelektrisk effekt [7]foton [6]friktion [53]friktionskoefficient [5]frågelådan [14]Fukushima [6]fusion [17]fysik [10]fysik, förståelse av [17]fysik, historia [1]fysik, nytta med [6]fysikalisk modell [12]färg/färgseende [39]färgkraften [8]Gaia [3]galax [28]gamma ray burst [2]gaslagen, allmänna [24]generator [1]genomskinlighet [18]genteknik [2]geodesi/gravimetri [2]geostationär satellit [8]gitter [5]g-krafter [18]glasögon [2]gluoner [7]glödlampa [23]gnistkammare [1]golfboll [15]GPS [3]gravitation [7]gravitationslins [5]gravitationsvågor [19]gravity assist [2]gregorianska kalendern [1]grundämnen, bildandet av [5]grundämnen, förekomst [4]gränshastighet [4]gunga [4]gyroskop [1]halofenomen [2]halogenlampa [3]halveringstid/sönderfallskonstant [5]harmonisk svängning [4]Heisenbergs obestämdhetsrelation [12]helikopter [5]higgspartikeln [10]Hiroshima/Nagasaki [4]hologram [5]HR-diagram [3]Huygens princip [3]hyperfinstruktur [1]hägring [4]händelsehorisont [4]hävstång [5]hörsel [10]Illustrerad Vetenskap [17]impedans [3]induktans [6]induktion [13]inertialsystem [6]inflation [7]infraljud [7]interferens [14]Internationella rymdstationen [6]iskristaller [5]istider [8]joniserande strålning [4]jordens atmosfär [12]jordens inre [14]jordens magnetfält [22]jordens rotation [22]kall fusion [8]kaos [3]kapillärkraft [12]kastparabel [10]Keplers lagar [14]Kirchhoffs strålningslag [4]klimat [11]knäppande aluminiumfolie [2]kokande vatten [17]kokpunkts/fryspunkts förändring [14]kol [3]kol-14 metoden [4]koldioxidcykeln [6]kollisionssäkerhet [1]komet [14]kosmisk bakgrundsstrålning [19]kosmisk strålning [5]kosmologi [33]kraft [12]kraftledning [7]kraftverkningar [9]kursplan [3]kvantmekanik [30]kvark [12]kvasar [4]kylning [7]kärndata [3]kärnenergi [19]kärnfysik [2]kärnkrafter [7]kärnkraftsavfall [11]kärnreaktion [5]kärnvapen [16]Lagrange-punkt [2]latitud/longitud [1]lins [11]liv i universum [9]livets uppkomst [1]ljud [11]ljud, interferens [7]ljud, resonans [19]ljudbang [3]ljudhastigheten [21]ljusbrytning [26]ljushastigheten [24]ljusreflektion [18]lorentztransformation [2]luftmotstånd [11]lufttryck [23]luminiscens [5]lutande plan [15]lysdiod [14]lysrör [10]lågenergilampa [13]längdkontraktion [6]magnetisk monopol [4]magnetism [52]magnetron [1]Mars [12]massa, trög/tung [4]massa-energi [1]massa-kraft [1]massbestämning [2]mass-luminositetsrelation [2]matematik i fysik [6]matematik, skriva [2]materia [6]Maxwells ekvationer [3]metabolism [3]metall, smältpunkt [3]meteorit [21]mikrovågsugn [25]Milankovitch cykler [3]mobiltelefon, strålning från [6]monstervåg [4]Monte Carlo-metoder [1]Mpemba-effekten [2]MRI [5]musikinstrument [19]månens bana [14]månens synbara storlek [1]månfärder [7]mörk energi [6]mörk materia [17]nanoteknik [6]Nationalencyklopedin [1]naturkonstant [7]naturlig radioaktivitet [3]nebulosa [13]NEO [10]neutrino [19]neutron [4]neutronstjärna [11]Newtons gravitationslag [12]Newtons rörelselagar [21]Newtons vagga [2]norrsken [7]nova [1]nyheter [11]Olbers paradox [2]orgelpipa [4]osmos [8]parallaxmetoden [4]parapsykologi [6]parbildning [7]Pascals lag [5]pauliprincipen [10]pendel, konisk [2]pendel, plan [9]PET [1]Plancks strålningslag [6]planet [17]planeters atmosfär [4]planeters form [3]plastfolie [1]polarisation [7]polaroidglasögon [3]potential/potentiell energi [30]prisma [1]projektarbete [1]pseudovetenskap [11]QED [7]radioaktiv datering [7]radioaktivitet, sönderfallskedja [7]radioaktivt sönderfall [38]radioteleskop [1]radon [4]raketekvationen [2]raketmotor [8]regn [1]regnbåge [6]relativistiskt massberoende [4]relativitetsteorin, allmänna [33]relativitetsteorin, speciella [45]religion [3]resistans [15]resistansförluster [2]resonans [5]richterskalan [2]ringklocka [5]rymddräkt [5]rymdfärder [23]rödförskjutning [7]röntgenrör [3]rörelseenergi [14]rörelsemängd [15]rörelsemängdsmoment [14]satellitbana [15]Saturnus´ ringar [6]schrödingerekvationen [4]Schrödingers katt [2]science fiction [6]segling [5]serie- och parallellkoppling [19]SETI [1]shareware [1]SI-enheter [6]skruvad boll [10]skymning [1]slumptal [1]SN 1987A [4]solaktivitet [2]solarkonstanten [6]solcell [7]solen [5]solen, avstånd till [1]solenergi [14]solens energiproduktion [9]solens utveckling [4]solförmörkelse [3]solsystemet [8]solsystemet, avstånd och rörelse [3]solsystemets bildande [12]specifik värmekapacitet [25]spegel [10]spektrum [11]standardmodellen [24]statisk elektricitet [12]stearinljuslåga [16]stjärna [4]stjärnhimlen [12]stjärnors utveckling [15]stroboskopeffekt [3]strålning, faror med [26]strålning, in-/ut- [6]strängteori [7]strömning [1]supernova [13]supertunga grundämnen [1]supraledning [7]svart hål [51]synvilla [6]sönderfallskonstant [5]teleskop [10]temperatur/temperaturskalor [17]temperaturstrålning [29]termodynamik [17]termometer [8]termos [3]Three Mile Island [3]tid [10]tidsdilatation [6]tidsekvation [4]tidvatten [15]tjerenkovstrålning [2]Tjernobyl [12]totalreflektion [9]transformator [6]transmutation av kärnavfall [2]trefas [3]trippelpunkt [2]tröghetsmoment [9]tsunami [5]tunneleffekt [3]TV [9]tvillingparadoxen [5]tyngdaccelerationen [16]tyngdlöshet [13]ultraljud [9]universums expansion [16]uppvärmning av bostäder [2]utvidgning [8]UV-ljus [13]vakuum [9]vatten/is [49]vattenkraft [7]vattenpump [2]vattenånga [2]Venus [11]verkningsgrad [26]vetenskaplig metod [18]Wikipedia [5]WIMPs [3]vindavkylning [4]vindenergi [12]Vintergatan [6]vridmoment [7]vulkanism [5]våg/partikelegenskaper [8]vågenergi [3]vågfunktion [2]värmemängd [3]värmepump/kylskåp [8]värmeöverföring/transport [46]väteatomen [2]vätskedroppsmodellen [5]växthuseffekten [36]ytspänning [18]årstider [4]ögat [18] (Enda villkor)
Definition:	(transmissions)mediumabsoluta nollpunktenabsorptionsspektraaccelerationackommodationackretionsskivaadiabatisk processaerodynamic heatingaerosolaggregationstillståndakustisk impedansallmänna gaslagenampereamperetimmeannihilationantigravitationantimateriaantropiska principenarbetearkimedes principasteroidasteroidbältetastigmatismastrobiologiastronomisk enhetatommassaatomnummeravogadros talbandspektrabatteribenhams snurrabergvärmebernoullis ekvationbetasönderfallbig bangbindningsenergibindningsenergibioluminiscensboltzmanns konstantbose–einstein-kondensatbrewstervinkelnbrownsk rörelsebrytningsindexbrännpunktbubbelkammarecarnotprocesscentrifugalkraftcentripetalkraftcirkumpolära stjärnorcitronbattericorioliskraftencurietemperaturendarwins evolutionsteoride broglie våglängdendecibeldeltonden kosmologiska principendensitetdielektrisk polarisationdielektriskt materialdiffus reflektiondiffusiondigitalkameradimensiondioptridiskret spektrumdispersiondopplereffektdotternukliddulong-petits lage=mc2ekliptikanekoekvivalensprincipenelasticitetelastisk energieldelektrisk dipolelektrisk laddningelektrisk spänningelektrisk strömelektriska fältstyrkanelektroluminiscenselektromagnetisk strålningelektroninfångningelektronskalelementarladdningenelementarpartiklaremissionsnebulosaemissionsspektraemsendoterm reaktionenergienergikällaenergiomvandlingenergipincipenenergipotentialentropi (makroskopisk definition)entropi (mikroskopisk definition)evighetsmaskinexciterade tillståndexoplanetexoterm reaktionextremofilerfallrörelsefaradays burfasdiagramfermats principferminivånferromagnetismfissionfjärde generationens reaktorfluidfluorescensflygplansvingeflykthastighetenfokalpunktfokusfosforescensfossila bränslenfotokromismfotomotståndfotonfotosfärenfotosyntesfouriers lagfraktalfranck-hertz försökfriktionfriktionskoefficientfritt fallfukushimafundamentala naturkrafternafusionfysikfysikaliska modellerfysiologifärgfärgblindhetfärgseendefönybara bränslenförnybara energikällorgaiagalaxgammastrålninggaskonstantengeneratorgeostationär satellitgeotermisk energiglobal uppvärmninggluonerglödlampagravitationgravitationengravitationskonstantengravitationsvågorgrundläggande fysikgrundtillståndetgrundtongrundämnegrå starrgränshastighetgula fläckenhalleffekthalogenlampahalveringstidhastighethawkingstrålningheisenbergs obestämdhetsrelationhertzsprung-russell diagramhiggspartikelnhookes laghornhinnanhubble ultra deep fieldhuygens principhydrostatiska paradoxenhägringhändelsehorisontenhästkrafthävstångicke-joniserande strålningideal gasimpedansinduktansinduktioninertialsysteminflationinfraljudinfraröd strålninginklinationinre konversioninre resistansinterferensinverterad populationisomerisospinnisoterm processisotoperjondriftjoniserande strålningjordfelsbrytarekalibreringkall fusionkalorikapacitanskapillärkraftenkastparabelkedjereaktionkemisk bindningkemisk bindningkemisk reaktionkemoluminiscenskeplers andra lagkeplers första lagkeplers tredje lagkilogramkirchhoffs lagkirchhoffs strålningslagkiselklassisk fysikklorofyllkokarreaktorkokpunktkolkornsmikrofonkometkomplementfärgkondensatorkonduktanskonservativ kraftkonserveringslagkontinuerligt spektrumkonvektionkoronankorrespondesprincipenkosmiska bakgrundsstrålningenkosmologikosmologiska rödskiftetkosmologiska standarmodellenkraftkristallkritisk densitetkritisk massakromosfärenkuiperbältetkundts rörkvantdatorkvantmekanikkvantmekanisk sammanflätningkvarkkvark-gluon plasmakvartskvasarkvasipartiklarkärnkrafterkärnreaktionkärnreaktorerkärnvapenlagrange-punkternalaserlenz lagleptonlila linjespektralivljudljusljusabsorptionljusbrytningljushastighetenljuskällorljusutbyteljusårlongitudinell våglorentzkraftenluftmotståndluminiscenslutande planlysdiodlysrörlågenergilampalägesenergilängdkontraktionmachomagnetismmagnuseffektenmarkradarmarkvärmemaskhålmassamasscentrummassdefektmassenhetmassexcessmasstalmateriamaxwell–boltzmannfördelningenmaxwells ekvationermedelvärdetmegaton tntmeissnereffektenmekanikens gyllene regelmerkurius periheliumprecessionmetafysikmetallbindningmetalldetektormetallicitetmeteormeteoritmeteoroidmilankovitch cyklermodern fysikmodernuklidmolmolekylmultiversummymetallmånemätfelmörk energimörk materiamörk nebulosamössbauer-effektennanometertekniknanopartikelnanotekniknationalencyklopedinnaturvetenskapnavigeringneoneutrinoneutrinooscillationerneutroninducerad fissionneutronstjärnanewtonnewtonringarnewtons andra lagnewtons avsvalningslagnewtons första lag (tröghetslagen)newtons gravitationslagnewtons tredje lagnobelpris i fysik 1925nobelpris i fysik 1993nobelpris i fysik 2015nobelpris i fysik 2017nobelpris i fysik 2020normalkraftennorrskennuklidnuklidkartanutida fysiknärsynthetockhams rakknivohms lagoorts kometmolnoregelbunden galaxosmosparapsykologiparbildningpascals princippauliprincipenperiodiska systemetplanck timeplancks strålningslagplanetplanetarisk nebulosaplasmaplasmaplasmaplasticitetpn-övergångpolarisationpolspänningpolär jetstrålepotentialproton-protonkedjanpseudovetenskapqcdqedradiative forcingradioaktivitetradioluminiscensraketekvationenrayleigh-spridningreaktansreflektionreflektionsnebulosarefraktionregnbågerelativ luftfuktighetrelativistisk energirelativistisk jetresistansresistivitetresistivitetresonansroche-gränsenrullmotståndrussells tekannarödförskjutningrörelseenergirörelsemängdrörelsemängdsmomentschwarzschildradiensekulär jämviktsekundsfärisk aberrationsi-enheternasingularitetsi-prefixsi-systemetsjälvinduktansskalärproduktskottsekundslipstreamslumpvisa mätfelsmältvärmesnells lagsolarkonstantensolcellersolenergisolens centrumsolförmörkelsesolkraftverksolvindsolvärmespallationspecifik värmekapacitetspektroskopispektrumspinnspontan fissionstandardavvikelsenstandardmodellenstatisk elektricitetstefan–boltzmanns lagstimulerad emissionstjärnastjärnbildstorhetstrålningstrålningstråloptiksträngteorinstående vågstämgaffelsublimationsupermassiva svarta hålsupernovasupertungt grundämnesuprafluiditetsupraledningsvart hålsvartkroppsvänghjulsystematiska mätfelsåpbubblasäkringsönderfallskedjasönderfallskonstantentemperaturtemperaturspektrumtemperaturstrålningtensortermodynamiktermodynamikens andra huvudsatstermodynamikens första huvudsatsthree mile islandtidtidens riktningtidsdilatationtidsekvationentidvattentidvattenkraftertillämpad fysiktjerenkovstrålningtjernobyltotalreflektiontransformatortransistortransparenstriboelektrisk effekttrippelpunktentrycktryckvattenreaktortröga massantröghettröghetsmomenttunga massantvillingparadoxentyngdtyngdaccelerationtyngdlöshettyngdpunktentyp ii supernovaufoultraljudultraviolett strålningultraviolettkatastrofenunderkylninguniversums åldervakuumvakuumfluktuationervakuumpolarisationvalenselektronvattenburen värmevattenkraftvattenkraftvattenångavektorerverkningsgradvetenskaplig metodwiens förskjutningslagwikipediaviktwimpvindkraftvintergatanvintergatanvirtuell bildvirtuell bildvit dvärgvoltvridmomentv-t diagramvåglängdenvåg-partikeldualitetvågtalvärmeledningvärmemängdvärmepumpvärmepumpvärmeöverföringvätebindningvätelika jonervätskedroppsmodellenväxthuseffektenytenergiångbildningsvärmeångtryckårstidernaåskaädelgasädelgaserögats linsöratöversynthetövertoner (Enda villkor)

---

Om du inte hittar svaret i databasen eller i

Sök i svenska Wikipedia:

Sök i Nationalencyklopedin

   

Sök med Google

   

- fråga gärna här.