I praktiken verkar detta inte riktigt vara sant dock, utan det verkar diffa på några centimeter var buken på den stående vågen ligger. Om man mäter längden på resonanslådan( halvöppen låda) till en stämgaffel med ton a ( 440 Hz) så är den ca 17,5 cm lång ( invändigt). Med ljudhastigheten 340 m/s borde lådans längd snarare vara 19,3 cm ( = 340/440) /4.

Ligger buken till den stående vågen någon centimeter utanför rörets öppning? Går det att förklara detta på nåt vettigt sätt för mig som gymnasielärare och för mina gymnasieelever?
/Linda G, Hulebäcksgymnasiet, Mölnlycke

Svar:
Linda!

Fysik är ju en experimentell vetenskap med förenklade modeller, se fråga 20588 . Oavsett hur sofistikerad en modell är, så är det experimentet som gäller.

Svagheten med den enklaste modellen som du använder är att man inte tar hänsyn till pipans diameter. Intuitivt kan man nog acceptera att buken i den öppna änden inte plötsligt vänder utan att det finns en "övergångssträcka". Detta betyder att den verkliga våglängden blir större än vad den uträknade modellen säger.

Citat från länk 1:

The effective length of an organ pipe is larger than its physical length by an amount called the end correction which for every open end is approximately 0.3×diameter of the organ pipe.

So two organ pipes of the same length but different diameters will have different resonant frequencies the one with the larger diameter being lower in frequency.

Låt oss se vad ovanstående korrektion gör för skillnad. Vi gissar att rörets diameter (i ditt fall antagligen en fyrkant) är 5 cm.

Korrigerad längd = 17.5+0.3*5 = 19.0 cm

vilket stämmer väl med ditt värde 19.3 cm.

Se även fråga 12744 och 20778 .
/Peter E

Nyckelord: ljud, resonans [19]; fysikalisk modell [12];

1 https://physics.stackexchange.com/questions/247508/does-the-frequency-of-a-organ-pipe-changes-with-its-diameter-explain

Jag har antagit ett övertryck, räknat ut Fres genom formeln p x A och sedan använt mig av Fres = m x a. Fick fram m genom densiteten för luft x volymen på ballongen (antagit en radie på 10 cm och formen av ett klot). Bytt ut a till delta v/ delta t ... Har att t = 1 s så jag får fram att Fres = densiteten för luft x volymen på ballongen x delta v. Jag har Fres från p x A och räknar ut massan... får ut att v blir 587 m/s. Är det ens rimligt?? Det känns verkligen inte rätt hahaha.

Skulle uppskatta all hjälp, både med teorin (tankesättet) och uträkningen... Är osäker på allt.
/Sara K

Svar:
Hej Sara! Ibland kan till synes enkla problem vara mycket svåra att lösa. Ditt problem går inte att lösa med de uppgifter du ger. Var har du fått det ifrån?

Det som i första hand bestämmer hur högt ballongen flyger är ballongens elasticitet. Det kan du säkert förstå om du tänker dig en ballong som inte utvidgar sig, t.ex. en plastballong, se fråga 19631 . Plastballongen skulle inte flyga alls, medan en elastisk gummiballong flyger några meter.

Allt som sker med ballongen styrs naturligtvis av fysikens lagar (gaslagen, bevarande av rörelsemängd, luftmotstånd mm) men även ett enkelt system som en ballong blir alltför komplex för att räkna på den. Vad man ofta gör i sådana fall är att man konstruerar en förenklad modell som man kan jämföra med mätningar.

Sedan finns det även mer grundläggande skäl att inte allt kan förutses från fysikaliska lagar. Olika fysikaliska effekter som påverkar systemet kan växelverka med varandra, för att göra det ännu svårare kan växelverkan vara olinjär. Se även fråga 951 för ännu mer grundläggande begränsningar för en teoretisk beskrivning.
/Peter E

Nyckelord: fysikalisk modell [12];

Ursprunglig fråga:
Jag är lite nyfiken på hur ni experter inom fysik skulle tolka följande textrad hämtad ur LGR11, kunskapsmålen i fysik för åk 6:

"Dessutom förklarar eleven och visar på mönster i himlakroppars rörelse i förhållande till varandra..."

Det är ett kriterium för betyget A. Det som skiljer målen för A från kunskapsmålet på nivå C (som är lägre) är att då behöver eleven istället för att se mönster i rörelserna visa på samband kring himlakroppars rörelse i förhållande till varandra.

Jag har undervisat eleverna i min åk 5 om hur bl.a. planeterna rör sig runt solen och hur månar rör sig kring planeter. Vi har pratat om att gravitationen håller planeter och månar i sina omloppsbanor och att gravitationen påverkar kroppar som är nära mer än kroppar som befinner sig långt ifrån. Vi har pratat om att det är anledningen till att planeterna närmast solen rör sig snabbare i sina omloppsbanor jämfört med planeterna längre bort. Generaliseringen som vi gjort är att himlakroppar med större massa och gravitation håller kroppar med mindre massa och gravitation i omloppsbana istället för tvärtom. Men vi har också resonerat om att de mindre kropparna också drar i de större och skapar en "wobblande" rörelse hos dem.

Hur tolkar ni skillnaden mellan att se mönster och se samband kring himlakropparnas rörelser. Är det något som jag borde ta upp mer med mina elever för att komma ner på det djup som kunskapsmålet riktar in sig på?

Med vänlig hälsning Petri Matalamaa
/Petri M, Paulinska skolan, Strängnäs

Svar:
Hej Petri! Jag håller i stort med om kunskapsmålen och tycker det låter som att du uppfattat dem mycket bra.

För det första är jag allergisk mot begreppet förklara när det gäller fysikens lagar. Förklara är för mig svar på frågan varför?. I djupare mening vet vi inte varför naturlagarna är som de är, se fråga 12126 .

Fysik är en empirisk vetenskap som i grunden bygger på observationer och experiment, se fråga 14232 . Fysiken använder matematik som ett verktyg, men fysik är inte matematik. Ofta utgår man från ett antagande och detta antagande kan sedan få stöd genom direkta eller indirekta observationer. Einstein antog t.ex. att ljushasigheten i vakuum är konstant när han utvecklade sin speciella relativitetsteori, och denna har visat sig stämma mycket väl.

Från Tycho Brahes mycket exakta mätningar av planeten Mars' rörelse (slutet av 1500-talet) kunde Johannes Kepler (i början av 1600-talet) få fram tre lagar för planeternas rörelser. Samtidigt använde Gallileo Gallilei det nyuppfunna teleskopet för att göra astronomiska observationer. Han studerade även, både teoretiskt och experimentellt, kroppars rörelse.

Isaac Newton kunde senare (andra hälften av 1600-talet) "förklara" planeternas rörelser med hjälp av en lag, den universella gravitationslagen och nyutvecklad matematik (differentialkalkyl).

Den ovanstående utgör det centrala i utvecklingen av den moderna vetenskapliga metod som används i naturvetenskapen, se fråga 14237 .

En annan viktig aspekt på fysik är att fysikaliska lagar inte är huggna i sten, utan de kan modifieras allteftersom vi gör bättre observationer.

Lagarna kan emellertid inte ändras hur fritt som helst, utan de måste alltid kunna reproducera alla befintliga mätresultat. Einsteins allmänna relativitetsteori beskriver gravitationen på ett utmärkt sätt, men den är mycket olik Newtons gravitationsteori. Det betyder inte att Newton hade fel, bara att det fanns begränsningar i giltigheten. Man använder t.ex. forfarande Newtons teori för att beräkna banor för rymdsonder.

I fysik använder man sig ofta av förenklade modeller som beskriver ett fysikaliskt fenomen med begränsade förutsättningar, se fråga 18296 . I kärnfysik betraktar man t.ex. ibland atomkärnan som en vätskedroppe och ibland som nukleoner som rör sig fritt i en potential (skalmodell). Modellerna är egentligen helt inkompatibla, men de är ändå av värde eftersom de båda "förklarar" olika egenskaper hos atomkärnor.

Och nu äntligen till din fråga:

Begreppet "förklarar" i texten ovan får man tolka så att man kan beskriva ett fenomen på en djupare nivå. Låt oss ta solens rörelse. Den dagliga rörelsen från öster till väster "förklaras" av att jorden roterar kring sin axel.

Solen rör sig även lite från väster till öster i förhållande till de avlägsna stjärnorna. Detta "förklaras" av att jorden rör sig ett varv runt solen på ett år. För att få ett A måste vi även kunna beskriva att den årliga rörelsen beskrivs av Newtons gravitationslag.

Den "wobblande" rörelsen du talar om uppkommer eftersom två kroppar rör sig i elliptiska banor kring den gemensamma tyngdpunkten. Om mass-skillnaden mellan kropparna är stor ligger den gemensamma tyngdpunkten nära den tyngre kroppens centrum. Detta betyder att den tyngre kroppen rör sig mycket lite.

Ett annat exempel är solsystemets uppbyggnad. Vi kan observera att planeterna alla rör sig åt samma håll och i ett plan. Detta kan "förklaras" genom modellen att solsystemet bildats genom att ett gasmoln dras samman av gravitationen. Bevarande av rörelsemängdsmomentet (se fråga 12527 ) ger då upphov till en roterande skiva av gas och stoft. Denna bildar sedan planeterna i ett plan och rörelse åt samma håll.

I fråga 16776 beskrivs solsystemets rörelse i vintergatan och universum.
/Peter E

Nyckelord: fysik, förståelse av [17]; vetenskaplig metod [18]; fysik [10]; fysikalisk modell [12]; kursplan [3];

1 http://pimlab.learnify.se/learnifyer/ObjectResources/f9c9e402-4879-4502-8f4c-ee6fc78fb396/Kunskapskrav.pdf

Ursprunglig fråga:
Naturvetenskapen beskriver modeller av sådant vi egentligen aldrig sett.

Hur kan man veta något om universums byggnad när man aldrig varit utanför vårt solsystem? Hur kan man veta något om jordens innandöme när det djupaste borrhålet i jordskorpan är 12 km? Hur kan man göra en modell av atomen när ingen har sett hur den ser ut?

Vad menas med att något har besvarats objektivt? Vad är motsatsen? Kan man någonson vara helt objektiv? Vad skulle kunna förhindra att något är helt objektivt?

Kan man vara naturvetare och samtidigt tro på gud?
/sofia k, skolstaden, olympia, Helsingborg

Svar:
Hej Sofia! Mycket bra men svåra frågor du ställer!

Naturvetenskap

I naturvetenskap har man för det första några grundregler som kallas vetenskaplig metod, se fråga 13406 . I fråga 14237 diskuteras god vetenskaplig metod och dess motsats, pseudovetenskap.

Vad gäller fysikaliska modeller så är de förenklade bilder av verkligheten som hjälper oss att förstå världen omkring oss. Modeller är inte detsamma som verkligheten, men en bra modell skall beskriva observationer så bra som möjligt.

Några exempel på fysikaliska modeller

Grunden för alla fysikaliska modeller är observationer och experiment. För kosmologi kan vi t.ex. observera den kosmiska bakgrundsstrålningen, mäta heliumhalten i stjärnor med spektroskopi, se att universum expanderar med dopplereffekten och mäta ljusstyrkan hos supernovor. Allt detta tillsammans skall passa in i en acceptabel modell för universums utveckling och struktur.

För jordens inre har man skaffat sig kunskap genom att studera sesmiska vågor vid t.ex. jordbävningar, se fråga 1052 . Dessutom kan man ju analysera material som kommer ut vid vulkanutbrott.

Bohrmodellen, fråga 13733 , beskriver atomen mycket förenklat. Den är en bra utgångspunkt men ger intrycket att elektroner rör sig i fixa banor.

Vätskedroppsmodellen är en enkel modell av atomkärnan som trots sin enkelhet förklarar förvånansvärt många egenskaper hos atomkärnor, se Vätskedroppsmodellen .

För att försöka förstå problemet med global uppvärmning använder man enkla och mycket sofistikerade klimatmodeller, se fråga 16846 .

För gravitation använder man fortfarande oftast Newtons beskrivning även om Einsteins allmänna relativitetsteori är mer grundläggande och mer korrekt i vissa fall. Det är inte ovanligt att man använder olika modeller för samma fenomen, aningen för att räkningarna blir enklare eller för att man bara är intresserad av en viss aspekt hos fenomenet.

Objektivitet

Objektivt är något som inte beror på observatören, och detta är något man strävar efter i naturvetenskap. Om du står på marken och släpper en boll, så kan nog alla vara överens om att bollen faller till marken. Om du däremot ställer frågan "vilken färg har bollen?", så kan du tänkas få olika svar eftersom hur man uppfattar färger är något subjektivt (motsatsen till objektivt).

Hundraprocentig objektivitet är mycket svårt att åstadkomma eftersom man redan när man bestämmer hur ett experiment eller en observation skall utföras, så har man infört ett mått av subjektivitet.

Religion

Ja, det finns många exempel på naturvetare som trott på Gud. Einstein är ett exempel.

Stephen Hawking är däremot ett exempel på en forskare som anser att det inte finns något behov av en gud, se fråga 17334 . Carl Sagan hade en ganska avvisande attityd till religion.

Många naturvetare föreställer sig inte en personlig gud utan något mer abstrakt, kanske t.o.m. att man uppfattar naturlagarna som ett gudomligt väsen.

Se även Vetenskapsteori , länk 1 och Fysik#Teori_och_experiment .
/Peter E

Nyckelord: vetenskaplig metod [18]; fysikalisk modell [12];

1 http://www.imit.kth.se/courses/2B1120/lecture/F1-modeller-energi.pdf

Ursprunglig fråga:
Hej! Jag har tre frågor:

1. Vad är supersträngar?

2. Hur skulle universum se ut, och vad skulle vara annorlunda om vi hade <2 eller 4< rumsdimensioner?

3. Vad menas med att tyngdkraften är additiv? Innebär det att den är tio gånger så stor i en kropp med tio atomer än vad den är i en ensam atom, och 10^9 gånger starkare i en kropp med 10^9 atomer osv.?
/Axel O, Södermalmsskolan, Stockholm

Svar:
Axel! Detta är mycket svåra men aktuella frågor. Eftersom Stephen Hawking och Leonard Mlodinow just kommit ut med en bok, The Grand Design (länk 1), kan det vara på sin plats att sammanfatta var strängteorin står i dag. Nedanstående är till en del baserat på en artikel i Sunday Times vetenskapsbilaga Eureka från september 2010.

Strängteorin innebär att man beskriver elementarpartiklar som små endimensionella strängar. Dessa strängar vibrerar med olika frekvenser för att bilda olika partiklar. Det visade sig att det finns minst fem olika sträng-teorier med 10 rum/tid-dimensioner. Så småningom kom man fram till att alla var ekvivalenta med en teori med 11 dimensioner: M-teorin.

M-teorin

Enligt vissa teoretiker är M-teorin den ultimata TOE (Theory of Everything). Hawking ser M-teorin som ett underliggande karta som håller ihop olika teorier som beskriver alla naturlagar.

Det tycks som om ingen vet vad M-et i namnet kommer ifrån. Förutom Maybe (kanske) har jag sett Master (huvud-), Miracle (mirakulös) och Mystery (mysterium). Det tycks som om M-teorin är allt detta !

I M-teorin har man alltså 11 rum/tid-dimensioner. Anledningen till att vi bara ser tre rumsdimensioner är att de övriga är kollapsade (eller kanske mer exakt, de har inte expanderat som de tre vi ser).

I M-teorin är man inte begränsad till endimensionella strängar, utan man kan ha vibrerande objekt (supersträngar) i 2 dimensioner (membran), 3 dimensioner (blobbar) och upp till 9 dimensioner.

Två fundamentala problem i dagens fysik är den spöklika obestämdheten hos kvantmekaniken (en atom kan befinna sig i flera tillstånd samtidigt) och det faktum att naturlagarna tycks vara finjusterade så att universum kunde utvecklas till ett universum som ger plats för liv - även om det bara finns på ett ställe, se diskussionen nedan.

M-teorin tillåter kanske 10⁵⁰⁰ olika universa med varierande naturlagar. Teorin tillåter, med hjälp av gravitationen, att universa skapas ur ingenting.

Universums utveckling och Guds existens

Mycket av diskussionen om Hawkings bok har handlat om behovet av en högre makt. Om man studerar universums utveckling från Big Bang till vad vi observerar i dag, visar det sig att många av naturlagarna verkar avstämda för att producera en värld där liv är möjligt. Några exempel (bland många) på denna finjustering av naturlagarna är

1. Om den starka kärnkraften bara varit lite starkare så hade ²He varit stabilt och stjärnor hade inte kunnat bildas.
2. Om det inte funnits ett tillstånd i ¹²C som precis passar till energin hos 3 a-partiklar, så hade ämnen tyngre än kol (som behövs för liv) inte kunnat bildas.
3. Endast ett universum med 3 utvecklade rumsdimensioner tillåter stabila planetbanor och följaktligen liv, åtminstone som vi känner det.

Ovanstående egenskaper kan förklaras på ett av tre sätt

1. Det finns en högre makt som bestämt att det skall vara så (den klassiska religiösa skapelseteorin).
2. Det är en ytterst osannolik slump.
3. Det finns massor av universa med olika egenskaper. Ett av dessa är vårt med de nödvändiga egenskaperna. De övriga "misslyckade" universa finns, men de innehåller inget intelligent liv som kan fundera på varför deras värld ser ut som den gör.

Hawking förespråkar punkt 3: Gud i punkt 1 behövs inte.

Några kommentarer

Eftersom M-teorin ännu inte kan knytas till observationer kan man ha olika åsikter om teorin:

Den är "Kejsarens nya kläder" eller pseudovetenskap av noll och intet värde. Eller Hawkings optimistiska åsikt att det kan vara den ultimata teorin som förklarar allting: "Philosophy is dead and there is no need for the God hypothesis: modern cosmology has all the answers".

Jag tror att de flesta av dagens fysiker anser att det är en lovande början och låter teoretikerna hållas ett tag till så de får en chans att komma upp med några förutsägelser som kan testas med experiment. Bilden nedan från ett föredrag av Lawrence M Krauss (se fråga 18978 ) är en mindre positiv synpunkt.

Jag har en kanske naiv uppfattning att en modell eller teori skall vara behjälplig för att "förstå" ett fysikaliskt fenomen. För mig uppfyller M-teorin inte detta kriterium med sina 10⁵⁰⁰ universa. Men för all del, redan kvantmekaniken är obegriplig.

Vad gäller din sista fråga, så har jag inte sett uttrycket, men jag tror din tolkning är korrekt: helt enkelt att kraften är proportionell mot massan, F=m*g.

Nyckelord: strängteori [7]; fysikalisk modell [12];

1 http://www.amazon.co.uk/Grand-Design-Stephen-Hawking/dp/0593058291/
2 http://superstringtheory.com/

Svar:
Erik! Nej, det är inte så enkelt! Dels vet jag mycket lite om detta, och dels är problemet komplext. I sådana fall får man ofta ta till enkla matematiska modeller som innehåller parametrar man kan bestämma experimentellt, t.ex. med vindtunnelmätningar.

Det är t.ex. uppenbart att kraften på masten varierar inte bara med vinden utan med hur mycket effekt man tar ut. Vridmomentet (som är vad man vill ha) ackompanjeras av en kraft på masten i vindriktningen, se Wind_turbine_design#Blade_design som för övrigt verkar vara en bra ingång i ämnet.

Såvitt jag förstår är de flesta fall när ett vindkraftverk går sönder att bladen bryts eller ramlar av - masten brukar hålla.
/Peter E

Nyckelord: vindenergi [12]; fysikalisk modell [12];

Vi hade 3 likadana pet-flaskor. En av dem var tom, en var fylld med vatten och en var fylld med sand. Vi släppte alla samtidigt ifrån en rutschbana. Först ner kom flaskan med vatten i. Sedan kom flaskan med sand och sist flaskan som var tom. Flaskan med vatten vägde 554 gram, flaskan med sand vägde 693 gram och flaskan som var tom vägde 31 gram. Alla flaskorna hade samma friktion.

Vi undrar varför flaskan med vatten kom före flaskan med sand.
/Sofia S, Kullaviksskolan, Kungsbacka

Svar:
Sofia! Problemet är inte helt enkelt - det finns flera effekter som kan spela en roll.

Enligt siffrorna du ger skulle sanden ha densiteten 1300 kg/m³. Det låter väldigt lite! Är du säker på att flaskorna med sand och vatten var helt fulla? Om inte, så kommer speciellt flaskan med sand ha en mycket stor inre friktion.

Hur uppför sig den tomma flaskan? Rullar den ner eller glider den? Om den glider är friktionen annorlunda än om den rullar.

Om experimentet, vilket jag tror, skall visa på effekten av tröghetsmoment och rotationsenergi, är det inte bra att flaskorna är fyllda med något som är mer eller mindre rörligt. Om man skall kunna dra några slutsatser av fysikaliska experiment bör man om möjligt bara variera en sak i taget (en parameter i vår modell i taget). Länk 1 visar ett experiment med rullande burkar där man ser till dels att tyngderna (brickorna, i texten kallade packningar) är fixerade till burken och dels att burkarna väger lika mycket (har samma antal brickor).

Idén med försöket är att när burken rullar ner så omvandlas den potentiella energin dels till vanlig rörelseenergi och dels till rotationsenergi. Burken med det högre tröghetsmomentet (den med bickorna ute i periferin) kommer att ha mer rotationenergi och därmed mindre rörelseenergi mv²/2. Hastigheten v blir då mindre än för burken med brickorna inne vid rotationsaxeln.

Som jag sa är det inte helt lätt att förklara resutatet från ert experiment eftersom flera egenskaper varieras på en gång.

Den tomma flaskan var långsammast och det bör bero på att det relativa tröghetsmomentet (tröghetsmomentet/kg massa) är störst för den tomma flaskan. Detta eftersom en stor den av massan för den tomma flaskan finns ute vid periferin.

Den vattenfyllda flaskan var snabbast ner. Jag tror att det beror på att kontakten mellan vattnet och flaskan inte är så bra. Vattnet i flaskan sätts alltså inte i rotation så mycket, så det blir mer energi över till rörelseenergi.

Flaskan med sand har samma relativa tröghetsmoiment (samma massfördelning), men sanden har bättre kontakt med flaskan (högre friktion), så sanden sätts mer i rotation än vattnet. Mer rotationsenergi betyder mindre rörelseenergi och därmed mindre hastighet.

Hoppas detta hjälper er lite i era bryderier!
/Peter E

Nyckelord: tröghetsmoment [9]; fysikalisk modell [12];

1 http://snacks.fysik.org/showSnack.asp?id=27

Jag är mycket intresserad av pertikelfysik och skulel bli väldigt glad för svar. :)
/Charlie L, Danderyds Gymnasium, Danderyd

Svar:
Charlie! Du skall inte blanda ihop verkligheten med en modell av verkligheten. Den bild du talar om är Feynman-diagram som är en beräkningsmetod inom kvantfältteorin, uppfunnen av den amerikanske fysikern Richard Feynman. Man beskriver visserligen den elektromagnetiska kraften som ett utbyte av fotoner, men dessa är virtuella så man kan inte tilldela dem några egenskaper. Fysikaliska modeller är ofta matematiska beskrivningar av fenomen, men de får inte övertolkas.

Feynmandiagram är en summarisk framställning, motsvarande engelska artikel Feynman_diagram är mer detaljerad men också svår. Quantum_electrodynamics ger en bra historisk introduktion.

Lästips:
Feynman, Richard (2006). QED: the strange theory of light and matter. Princeton University Press. ISBN 0-691-12575-9.

Länk 1 innehåller fyra föreläsningar av Richard Feynman.
/Peter E

Nyckelord: kraftverkningar [9]; fysikalisk modell [12]; QED [7];

1 http://www.vega.org.uk/video/subseries/8

Ursprunglig fråga:
Hej! Jag håller på och läser in kursen Fysik B och har problem med den matematiska rörelsebeskrivningen. I ett exempel som anges i kursboken är en matematisk modell över en 100-meterslöpares startförlopp:

v=10t-2.5t² samtidigt som t är mellan 0 och 2 sekunder (1)

Fråga: Hur långt har löparen enligt modellen kommit efter 2 sekunder?

I lösningen som anges börjar man med att utgå från regeln: ds/dt=v. Sedan anges, att s får bestämmas genom att göra en "primitiv funktion" till v, enligt:

s=5t²-2.5t³/3+C, där konstanten C sätts till 0 så att s=0 då t=0 (2)

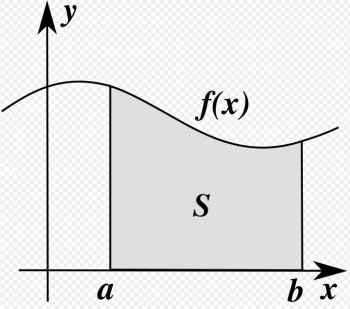
Mitt problem är att jag inte alls förstår hur denna "primitiva funktion" till v har bestämts. Hur får man stegvis fram denna funktion?? Hemskt tacksam för svar!
/Susanna A, Stockholm

Svar:
Susanna! Låt oss först beräkna accelerationen a = dv/dt. Hastigheten v ges av din ekvation (1). Derivatan av v med avseende på tiden t blir då

a = dv/dt = 10-5t

Anledningen till att accelerationen skrivs så här är ju att allteftersom löparens hastighet ökar, så måste accelerationen minska¹. Vi kan se att accelerationen enligt ovanstående modell är 0 vid t=2s. Då har löparen alltså uppnått sin sluthastighet. Om vi sätter in t=2s i (1) får vi slut(max)hastigheten 10 m/s.

Definitionen på hastighet är v=ds/dt. Hastigheten är alltså tidsderivatan vid en viss tidpunkt av den tillryggalagda sträckan. Se det så här: på den lilla tiden dt rör sig löparen sträckan ds. Hastighet är sträcka per tidsenhet alltså ds/dt.

Om vi våldför oss lite på matematiken kan vi se att ds=v*dt. Hastigheten v ges ju som funktion av t av (1). Vi kan då beräkna v for en massa värden från 0 till 2s och multiplicera med dt. Dessa ds kan vi sedan summera för att få den sträcka löparen tillryggalagt.

Matematiken bakom ovanstående kallas Infinitesimalkalkyl och utvecklades av Newton och Leibniz på 1600-talet (se Calculus och fråga 16084 nedan). Formellt är ds/dt något som kallas derivata. För att beräkna s från funktionen ds/dt måste vi integrera. Det finns massor med regler för derivering och integration (som man får lära sig i matematiken), men det viktiga i detta sammanhang är att integration är omvändningen till derivering. Så om vi integrerar ds/dt med avseende på tiden så får vi sträckan s.

Bilden nedan från Wikimedia Commons visar att integralen helt enkelt är ytan S under en funktion f(x). Integralen är alltså en yta, och räknas ut som en oändlig summa av pyttesmala rektanglar.

Hur får man då fram funktionen (2) från (1)? Ja, man måste kunna lite integreringsregler. Oftast är det emellertid enklare att derivera än att integrera, så låt oss kontrollera om (1) är derivatan av (2):

(d/dt)(5t²-2.5t³/3+C) = 10t-2.5t²

vilket alltså stämmer bra.

Det är naturligtvis måttligt intressant att beräkna hur en hundrameterslöpare spinger, men exemplet vill visa hur man i fysiken arbetar med matematiska modeller som sedan kan jämföras med verkligheten. Här är till sist en tabell med värden på a, v och s beräknade med ovanstående uttryck och med antagandet att löparen från 2 sekunder och framåt har den konstanta hastigheten 10 m/s.

  t     a     v      s
-------------------------
  0    10     0      0
  1     5    7.5    4.2
  2     0    10    13.3 
  3     0    10    23.3
  4     0    10    33.3
  5     0    10    43.3
  6     0    10    53.3 
  7     0    10    63.3
  8     0    10    73.3
  9     0    10    83.3
 10     0    10    93.3
 11     0    10   103.3

Hoppas detta hjälpte dig något!

¹ Till skillnad från en raket som accelererar snabbare och snabbare. Skillnaden beror på att för raketen är den största delen av massan bränsle, och detta försvinner ju efter hand som raketen accelererar.

Se även fråga 16084

Nyckelord: fysikalisk modell [12]; *idrottsfysik [42];

Svar:
För att förstå detta använder vi oss av en förenklad fysikalisk modell . Vi antar att sandkornet för enkelhets skull är sfäriskt med radien r och densiteten r.

Vindpåverkan V är proportionell mot tvärsnittsarean dvs

V = konst*p r².

Tyngdkraften T är proportionell mot massan dvs

T = m*g = (4p r³/3)*r*g.

Förhållandet T/V blir då

(4p r³/3)*r*g/(konst*p r²) = C*r

där C är en (ännu) obestämd konstant. Förhållandet är alltså proportionellt mot r, dvs ju större sandkornet är, desto mer dominerar tyngdkraften. När sandkornet blir riktigt stort (en sten) är T mycket större än V, varför vi får en resulterade kraft nästan rakt ner. Stenen påverkas alltså mycket lite av vinden.

Vi kan nu kontrollera om modellen är bra och i så fall bestämma konstanten C genom att göra mätningar i en konstant vind med sandkorn/stenar av olika storlek. Vi mäter avvikelsen från lodlinjen och plottar detta som funktion av radien r. Om resultatet blir en någotsånär rät linje kan vi bestämma C.

Konstanten C kommer antagligen att vara proportionell mot vindhastigheten i kvadrat. Genom att genomföra mätningar vid olika vindhastighet skulle man kunna verifiera detta samband.

I praktiken skulle det ovan beskrivna experimentet antagligen fungera mycket dåligt - vinden är i verkligheten aldrig konstant. Man skulle kunna förbättra försöket genom att utföra det inomhus med en stark fläkt. Om man i stället för fallande sandkorn använde sig av olika stora kulor av samma material som är upphängda i en tråd och mätte avvikelsen från lodlinjen, skulle man antagligen få ett bättre resultat.

Se även svaren om störloppsåkaren och bobåkarna: bobåkning/störtlopp .
/Peter E

Nyckelord: fysikalisk modell [12]; friktion [53];

Svar:
Se virvelström och virvelströmsbroms i Nationalencyklopedin . Se även nedanstående länkar.

Det går inte att ge en generell formel för den bromsande kraften, fenomenet är alltför komplicerat för detta, eftersom det beror av geometri, material mm. Det finns många fenomen inom fysiken som är alltför komplicerade för att beskrivas med en enkel formel. Man använder sig då ofta av vad vi kallar en modell.

Fysikalisk modell

För enkla fenomen som beskrivs i fysikböckerna (t.ex. magnetfältet utanför en lång rak ledare) finns en formel man kan tillämpa och få bra resultat. För komplicerade fenomen (t.ex. virvelströmmar eller jordens rörelse) finns ingen enkel formel.

Man kan då i vissa fall genom förenklande antaganden definiera ett matematiskt uttryck som beskriver hur det fenomen man vill förstå beror av ingående storheter. Detta uttryck innehåller då ofta fria parametrar - storheter med varierande värde. Genom att genomföra mätningar för olika värden på de ingående storheterna, kan man bestämma de bästa värdena på parametrarna. Man har då fått ett uttryck som beskriver fenomenet och detta uttryck kan sedan användas för att förutsäga utfallet för ett hypotetiskt experiment.
/Peter E

Nyckelord: fysikalisk modell [12];

1 http://www.physlink.com/Education/AskExperts/ae572.cfm
2 http://snacks.fysik.org/showSnack.asp?id=38

Ursprunglig fråga:
Tack för dina tidigare svar. Detta kanske inte är en fråga om fysik, men jag är tacksam om du kan svara ändå.

Hur kommer det sig att något så "logiskt" som en dator kan välja ut slumpmässiga tal? Jag vet att det finns en slumpgenerator, men hur fungerar den i praktiken?

Tacksam för svar.
/Erik T, Nyvång, Dalby

Svar:
Erik! Det största problemet med att få fram slumptal är att få fram det första. När man väl fått det använder man det för att med avancerade algoritmer generera fler (egentligen pseudoslumptal). Detta är inte enkelt, och de vanliga algorimerna som finns i programmeringsspråk är ofta inte perfekta, men tillräckligt bra för de flesta ändamål.

Det första slumptalet kan t.ex. genereras från datorns klocka. Eftersom tidpunkten du startar programmet är slumpmässig (åtminstone första gången) kan man använda t.ex. millisekund-värdena som ett slumptal.

Bra slumptalsgeneratorer är alltså inte lätta att göra, så ämnet är en hel vetenskap.

Monte Carlo-metoder

Slumptal används en hel del i fysiken i s.k. Monte Carlo (MC) program (kallas så för att dom liksom casinot innehåller slumpmässighet). När man vill simulera komplicerade processer är det ofta bra att använda MC program som t.ex. följer en partikels kollisioner med materia, och varje enskild kollision slumpas med vikter som bestäms av fysikaliska lagar. De fundamentala fysikaliska lagarna (t.ex. sannolikheten för att en partikel skall spridas i en viss vinkel) är ofta välkända, men problemet kan vara alltför komplicerat för att kunna lösas analytiskt. Man simulerar därför verkligheten med en fysikalisk modell.

Se vidare slumptal och Monte Carlo-metoder i Nationalencyklopedin .
/Peter E

Nyckelord: slumptal [1]; Monte Carlo-metoder [1]; fysikalisk modell [12];

Ämnesområde	BlandatElektricitet-MagnetismEnergiKraft-RörelseLjud-Ljus-VågorMateriens innersta-Atomer-KärnorPartiklarUniversum-Solen-PlaneternaVärme
Sök efter
Grundskolan eller gymnasiet?	FörskolaGrundskolaGymnasiumLärarutbildning
Nyckelord:	#ljus [63]*astronomi/astrofysik och rymdfart [2]*biologi [20]*fysikaliska definitioner [1]*fysiologi [13]*geologi [16]*idrottsfysik [42]*kemi [22]*meteorologi [20]*miljöpåverkan [14]*nöjesparksfysik [12]*vardagsfysik [64]*verktyg [15]3d-bilder [6]aberration [1]absoluta nollpunkten [9]acceleration [6]accelerator [7]addition av hastigheter [2]aerosol [4]akustik [6]alfasönderfall [7]annihilation [14]antimateria [16]arbete [24]Arkimedes princip [32]asteroid [10]astrobiologi [9]astrologi [5]atomradie [8]Avogadros tal [3]ballong [25]bandgenerator [3]barometerformeln [1]batteri [25]belysning [6]bernoullieffekten [6]betasönderfall [15]big bang [37]bildskärmar [4]bindningsenergi [23]blixt [18]blå himmel [12]bobåkning/störtlopp [4]Bohrs atommodell [9]Bose-Einstein-kondensat [6]brandvarnare [2]bränslecell [3]centrifugalkraft [15]centripetalkraft [11]comptonspridning [3]corioliskraft [7]dagens längd [3]daggpunkten [2]dagjämning [6]Darwins evolutionsteori [8]de Broglie våglängd [1]decibel [11]delton [2]diffraktion [4]diffusion [1]dimensionsanalys [7]dimkammare [2]dopplereffekt (ljud) [3]dopplereffekt (ljus) [3]drickande fågeln [1]dubbelspalt [4]duschdraperi [2]Einstein, Albert [1]eko [3]elasticitet [4]elastisk stöt [12]elektrisk krets [7]elektrisk ström, hastighet [4]elektrisk ström, skada [6]elektromagnetisk strålning [21]elektronskal [12]elektrostatik [4]elsäkerhet [18]energikällor [26]energilagringssystem [7]enkelspalt [1]entropi [7]EPR, Bell, Aspect [3]evighetsmaskin [14]exoplaneter [17]fallrörelse [31]faradaybur [10]fasdiagram [7]felberäkning [6]Fermats princip [1]ferromagnetism [9]fiberoptik [4]fission [15]fluorescens [6]flygplansvinge [8]flykthastighet [4]formel 1 [2]forskningskarriär [1]fossila bränslen [13]fotoelektrisk effekt [7]foton [6]friktion [53]friktionskoefficient [5]frågelådan [14]Fukushima [6]fusion [17]fysik [10]fysik, förståelse av [17]fysik, historia [1]fysik, nytta med [6]fysikalisk modell [12]färg/färgseende [39]färgkraften [8]Gaia [3]galax [28]gamma ray burst [2]gaslagen, allmänna [24]generator [1]genomskinlighet [18]genteknik [2]geodesi/gravimetri [2]geostationär satellit [8]gitter [5]g-krafter [18]glasögon [2]gluoner [7]glödlampa [23]gnistkammare [1]golfboll [15]GPS [3]gravitation [7]gravitationslins [5]gravitationsvågor [19]gravity assist [2]gregorianska kalendern [1]grundämnen, bildandet av [5]grundämnen, förekomst [4]gränshastighet [4]gunga [4]gyroskop [1]halofenomen [2]halogenlampa [3]halveringstid/sönderfallskonstant [5]harmonisk svängning [4]Heisenbergs obestämdhetsrelation [12]helikopter [5]higgspartikeln [10]Hiroshima/Nagasaki [4]hologram [5]HR-diagram [3]Huygens princip [3]hyperfinstruktur [1]hägring [4]händelsehorisont [4]hävstång [5]hörsel [10]Illustrerad Vetenskap [17]impedans [3]induktans [6]induktion [13]inertialsystem [6]inflation [7]infraljud [7]interferens [14]Internationella rymdstationen [6]iskristaller [5]istider [8]joniserande strålning [4]jordens atmosfär [12]jordens inre [14]jordens magnetfält [22]jordens rotation [22]kall fusion [8]kaos [3]kapillärkraft [12]kastparabel [10]Keplers lagar [14]Kirchhoffs strålningslag [4]klimat [11]knäppande aluminiumfolie [2]kokande vatten [17]kokpunkts/fryspunkts förändring [14]kol [3]kol-14 metoden [4]koldioxidcykeln [6]kollisionssäkerhet [1]komet [14]kosmisk bakgrundsstrålning [19]kosmisk strålning [5]kosmologi [33]kraft [12]kraftledning [7]kraftverkningar [9]kursplan [3]kvantmekanik [30]kvark [12]kvasar [4]kylning [7]kärndata [3]kärnenergi [19]kärnfysik [2]kärnkrafter [7]kärnkraftsavfall [11]kärnreaktion [5]kärnvapen [16]Lagrange-punkt [2]latitud/longitud [1]lins [11]liv i universum [9]livets uppkomst [1]ljud [11]ljud, interferens [7]ljud, resonans [19]ljudbang [3]ljudhastigheten [21]ljusbrytning [26]ljushastigheten [24]ljusreflektion [18]lorentztransformation [2]luftmotstånd [11]lufttryck [23]luminiscens [5]lutande plan [15]lysdiod [14]lysrör [10]lågenergilampa [13]längdkontraktion [6]magnetisk monopol [4]magnetism [52]magnetron [1]Mars [12]massa, trög/tung [4]massa-energi [1]massa-kraft [1]massbestämning [2]mass-luminositetsrelation [2]matematik i fysik [6]matematik, skriva [2]materia [6]Maxwells ekvationer [3]metabolism [3]metall, smältpunkt [3]meteorit [21]mikrovågsugn [25]Milankovitch cykler [3]mobiltelefon, strålning från [6]monstervåg [4]Monte Carlo-metoder [1]Mpemba-effekten [2]MRI [5]musikinstrument [19]månens bana [14]månens synbara storlek [1]månfärder [7]mörk energi [6]mörk materia [17]nanoteknik [6]Nationalencyklopedin [1]naturkonstant [7]naturlig radioaktivitet [3]nebulosa [13]NEO [10]neutrino [19]neutron [4]neutronstjärna [11]Newtons gravitationslag [12]Newtons rörelselagar [21]Newtons vagga [2]norrsken [7]nova [1]nyheter [11]Olbers paradox [2]orgelpipa [4]osmos [8]parallaxmetoden [4]parapsykologi [6]parbildning [7]Pascals lag [5]pauliprincipen [10]pendel, konisk [2]pendel, plan [9]PET [1]Plancks strålningslag [6]planet [17]planeters atmosfär [4]planeters form [3]plastfolie [1]polarisation [7]polaroidglasögon [3]potential/potentiell energi [30]prisma [1]projektarbete [1]pseudovetenskap [11]QED [7]radioaktiv datering [7]radioaktivitet, sönderfallskedja [7]radioaktivt sönderfall [38]radioteleskop [1]radon [4]raketekvationen [2]raketmotor [8]regn [1]regnbåge [6]relativistiskt massberoende [4]relativitetsteorin, allmänna [33]relativitetsteorin, speciella [45]religion [3]resistans [15]resistansförluster [2]resonans [5]richterskalan [2]ringklocka [5]rymddräkt [5]rymdfärder [23]rödförskjutning [7]röntgenrör [3]rörelseenergi [14]rörelsemängd [15]rörelsemängdsmoment [14]satellitbana [15]Saturnus´ ringar [6]schrödingerekvationen [4]Schrödingers katt [2]science fiction [6]segling [5]serie- och parallellkoppling [19]SETI [1]shareware [1]SI-enheter [6]skruvad boll [10]skymning [1]slumptal [1]SN 1987A [4]solaktivitet [2]solarkonstanten [6]solcell [7]solen [5]solen, avstånd till [1]solenergi [14]solens energiproduktion [9]solens utveckling [4]solförmörkelse [3]solsystemet [8]solsystemet, avstånd och rörelse [3]solsystemets bildande [12]specifik värmekapacitet [25]spegel [10]spektrum [11]standardmodellen [24]statisk elektricitet [12]stearinljuslåga [16]stjärna [4]stjärnhimlen [12]stjärnors utveckling [15]stroboskopeffekt [3]strålning, faror med [26]strålning, in-/ut- [6]strängteori [7]strömning [1]supernova [13]supertunga grundämnen [1]supraledning [7]svart hål [51]synvilla [6]sönderfallskonstant [5]teleskop [10]temperatur/temperaturskalor [17]temperaturstrålning [29]termodynamik [17]termometer [8]termos [3]Three Mile Island [3]tid [10]tidsdilatation [6]tidsekvation [4]tidvatten [15]tjerenkovstrålning [2]Tjernobyl [12]totalreflektion [9]transformator [6]transmutation av kärnavfall [2]trefas [3]trippelpunkt [2]tröghetsmoment [9]tsunami [5]tunneleffekt [3]TV [9]tvillingparadoxen [5]tyngdaccelerationen [16]tyngdlöshet [13]ultraljud [9]universums expansion [16]uppvärmning av bostäder [2]utvidgning [8]UV-ljus [13]vakuum [9]vatten/is [49]vattenkraft [7]vattenpump [2]vattenånga [2]Venus [11]verkningsgrad [26]vetenskaplig metod [18]Wikipedia [5]WIMPs [3]vindavkylning [4]vindenergi [12]Vintergatan [6]vridmoment [7]vulkanism [5]våg/partikelegenskaper [8]vågenergi [3]vågfunktion [2]värmemängd [3]värmepump/kylskåp [8]värmeöverföring/transport [46]väteatomen [2]vätskedroppsmodellen [5]växthuseffekten [36]ytspänning [18]årstider [4]ögat [18] (Enda villkor)
Definition:	(transmissions)mediumabsoluta nollpunktenabsorptionsspektraaccelerationackommodationackretionsskivaadiabatisk processaerodynamic heatingaerosolaggregationstillståndakustisk impedansallmänna gaslagenampereamperetimmeannihilationantigravitationantimateriaantropiska principenarbetearkimedes principasteroidasteroidbältetastigmatismastrobiologiastronomisk enhetatommassaatomnummeravogadros talbandspektrabatteribenhams snurrabergvärmebernoullis ekvationbetasönderfallbig bangbindningsenergibindningsenergibioluminiscensboltzmanns konstantbose–einstein-kondensatbrewstervinkelnbrownsk rörelsebrytningsindexbrännpunktbubbelkammarecarnotprocesscentrifugalkraftcentripetalkraftcirkumpolära stjärnorcitronbattericorioliskraftencurietemperaturendarwins evolutionsteoride broglie våglängdendecibeldeltonden kosmologiska principendensitetdielektrisk polarisationdielektriskt materialdiffus reflektiondiffusiondigitalkameradimensiondioptridiskret spektrumdispersiondopplereffektdotternukliddulong-petits lage=mc2ekliptikanekoekvivalensprincipenelasticitetelastisk energieldelektrisk dipolelektrisk laddningelektrisk spänningelektrisk strömelektriska fältstyrkanelektroluminiscenselektromagnetisk strålningelektroninfångningelektronskalelementarladdningenelementarpartiklaremissionsnebulosaemissionsspektraemsendoterm reaktionenergienergikällaenergiomvandlingenergipincipenenergipotentialentropi (makroskopisk definition)entropi (mikroskopisk definition)evighetsmaskinexciterade tillståndexoplanetexoterm reaktionextremofilerfallrörelsefaradays burfasdiagramfermats principferminivånferromagnetismfissionfjärde generationens reaktorfluidfluorescensflygplansvingeflykthastighetenfokalpunktfokusfosforescensfossila bränslenfotokromismfotomotståndfotonfotosfärenfotosyntesfouriers lagfraktalfranck-hertz försökfriktionfriktionskoefficientfritt fallfukushimafundamentala naturkrafternafusionfysikfysikaliska modellerfysiologifärgfärgblindhetfärgseendefönybara bränslenförnybara energikällorgaiagalaxgammastrålninggaskonstantengeneratorgeostationär satellitgeotermisk energiglobal uppvärmninggluonerglödlampagravitationgravitationengravitationskonstantengravitationsvågorgrundläggande fysikgrundtillståndetgrundtongrundämnegrå starrgränshastighetgula fläckenhalleffekthalogenlampahalveringstidhastighethawkingstrålningheisenbergs obestämdhetsrelationhertzsprung-russell diagramhiggspartikelnhookes laghornhinnanhubble ultra deep fieldhuygens principhydrostatiska paradoxenhägringhändelsehorisontenhästkrafthävstångicke-joniserande strålningideal gasimpedansinduktansinduktioninertialsysteminflationinfraljudinfraröd strålninginklinationinre konversioninre resistansinterferensinverterad populationisomerisospinnisoterm processisotoperjondriftjoniserande strålningjordfelsbrytarekalibreringkall fusionkalorikapacitanskapillärkraftenkastparabelkedjereaktionkemisk bindningkemisk bindningkemisk reaktionkemoluminiscenskeplers andra lagkeplers första lagkeplers tredje lagkilogramkirchhoffs lagkirchhoffs strålningslagkiselklassisk fysikklorofyllkokarreaktorkokpunktkolkornsmikrofonkometkomplementfärgkondensatorkonduktanskonservativ kraftkonserveringslagkontinuerligt spektrumkonvektionkoronankorrespondesprincipenkosmiska bakgrundsstrålningenkosmologikosmologiska rödskiftetkosmologiska standarmodellenkraftkristallkritisk densitetkritisk massakromosfärenkuiperbältetkundts rörkvantdatorkvantmekanikkvantmekanisk sammanflätningkvarkkvark-gluon plasmakvartskvasarkvasipartiklarkärnkrafterkärnreaktionkärnreaktorerkärnvapenlagrange-punkternalaserlenz lagleptonlila linjespektralivljudljusljusabsorptionljusbrytningljushastighetenljuskällorljusutbyteljusårlongitudinell våglorentzkraftenluftmotståndluminiscenslutande planlysdiodlysrörlågenergilampalägesenergilängdkontraktionmachomagnetismmagnuseffektenmarkradarmarkvärmemaskhålmassamasscentrummassdefektmassenhetmassexcessmasstalmateriamaxwell–boltzmannfördelningenmaxwells ekvationermedelvärdetmegaton tntmeissnereffektenmekanikens gyllene regelmerkurius periheliumprecessionmetafysikmetallbindningmetalldetektormetallicitetmeteormeteoritmeteoroidmilankovitch cyklermodern fysikmodernuklidmolmolekylmultiversummymetallmånemätfelmörk energimörk materiamörk nebulosamössbauer-effektennanometertekniknanopartikelnanotekniknationalencyklopedinnaturvetenskapnavigeringneoneutrinoneutrinooscillationerneutroninducerad fissionneutronstjärnanewtonnewtonringarnewtons andra lagnewtons avsvalningslagnewtons första lag (tröghetslagen)newtons gravitationslagnewtons tredje lagnobelpris i fysik 1925nobelpris i fysik 1993nobelpris i fysik 2015nobelpris i fysik 2017nobelpris i fysik 2020normalkraftennorrskennuklidnuklidkartanutida fysiknärsynthetockhams rakknivohms lagoorts kometmolnoregelbunden galaxosmosparapsykologiparbildningpascals princippauliprincipenperiodiska systemetplanck timeplancks strålningslagplanetplanetarisk nebulosaplasmaplasmaplasmaplasticitetpn-övergångpolarisationpolspänningpolär jetstrålepotentialproton-protonkedjanpseudovetenskapqcdqedradiative forcingradioaktivitetradioluminiscensraketekvationenrayleigh-spridningreaktansreflektionreflektionsnebulosarefraktionregnbågerelativ luftfuktighetrelativistisk energirelativistisk jetresistansresistivitetresistivitetresonansroche-gränsenrullmotståndrussells tekannarödförskjutningrörelseenergirörelsemängdrörelsemängdsmomentschwarzschildradiensekulär jämviktsekundsfärisk aberrationsi-enheternasingularitetsi-prefixsi-systemetsjälvinduktansskalärproduktskottsekundslipstreamslumpvisa mätfelsmältvärmesnells lagsolarkonstantensolcellersolenergisolens centrumsolförmörkelsesolkraftverksolvindsolvärmespallationspecifik värmekapacitetspektroskopispektrumspinnspontan fissionstandardavvikelsenstandardmodellenstatisk elektricitetstefan–boltzmanns lagstimulerad emissionstjärnastjärnbildstorhetstrålningstrålningstråloptiksträngteorinstående vågstämgaffelsublimationsupermassiva svarta hålsupernovasupertungt grundämnesuprafluiditetsupraledningsvart hålsvartkroppsvänghjulsystematiska mätfelsåpbubblasäkringsönderfallskedjasönderfallskonstantentemperaturtemperaturspektrumtemperaturstrålningtensortermodynamiktermodynamikens andra huvudsatstermodynamikens första huvudsatsthree mile islandtidtidens riktningtidsdilatationtidsekvationentidvattentidvattenkraftertillämpad fysiktjerenkovstrålningtjernobyltotalreflektiontransformatortransistortransparenstriboelektrisk effekttrippelpunktentrycktryckvattenreaktortröga massantröghettröghetsmomenttunga massantvillingparadoxentyngdtyngdaccelerationtyngdlöshettyngdpunktentyp ii supernovaufoultraljudultraviolett strålningultraviolettkatastrofenunderkylninguniversums åldervakuumvakuumfluktuationervakuumpolarisationvalenselektronvattenburen värmevattenkraftvattenkraftvattenångavektorerverkningsgradvetenskaplig metodwiens förskjutningslagwikipediaviktwimpvindkraftvintergatanvintergatanvirtuell bildvirtuell bildvit dvärgvoltvridmomentv-t diagramvåglängdenvåg-partikeldualitetvågtalvärmeledningvärmemängdvärmepumpvärmepumpvärmeöverföringvätebindningvätelika jonervätskedroppsmodellenväxthuseffektenytenergiångbildningsvärmeångtryckårstidernaåskaädelgasädelgaserögats linsöratöversynthetövertoner (Enda villkor)

---

Om du inte hittar svaret i databasen eller i

Sök i svenska Wikipedia:

Sök i Nationalencyklopedin

   

Sök med Google

   

- fråga gärna här.