Svar:
Hej Agnes! Jag är ingen expert på hopp i konståkning - mer en "Bambi på is" !

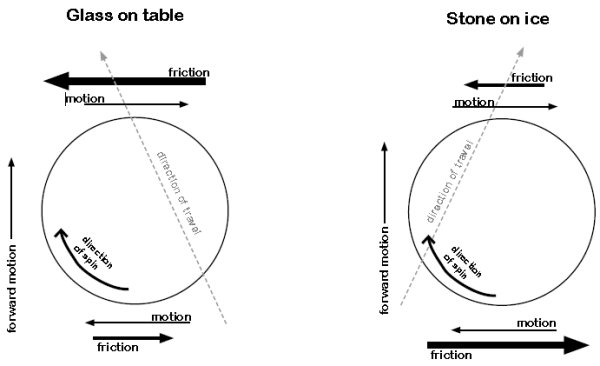
Jag är övertygad att kvintupler kommer med tiden, se länk 1 och 2. Om de kommer i tävling är tveksamt, men i uppvisning fullt möjligt.

Vad som krävs är hoppstyrka (hoppar du högre har du mer tid att rotera) och förmåga att rotera snabbt. Det finns ingen fysikalisk begränsning - det krävs "bara" spänst och styrka.

Förutom hoppstyrka kan man tänka sig att tekniken förändras.

Vad gäller utveckling av utrustning har till exempel hastighetsåkning på skridskor utvecklats genom införandet av klappskridskor, se Hastighetsåkning_på_skridskor#Klappskridsko . Jag vet inte om det är möjligt att utveckla konståkningsskridskor på något sätt.

Några kommentarer:

Hoppstyrka och förmåga att rotera snabbt

I många sporter (t.ex. golf och alpin skidsport) har fysisk träning blivit en förutsättning för bra resultat. Konståkare är säkert vältränade, men allt kan förbättras.

Förmågan att med en given kraft rotera så snabbt som möjligt är beroende av tröghetsmomentet (se Tröghetsmoment ) i förhållande till rotationsaxeln, så litet tröghetsmoment med smalt mellan axlarna och höfterna är vad fysiken vill ha. Som någon sagt: den optimale snurraren är en tråd med skridskor.

Utveckling av tekniken

Ett exempel på teknikutveckling är Fosbury flopp i höjdhopp (Fosbury-flopp ). Detta är antagligen mindre troligt i konståkning eftersom hoppen är mycket väldefinierade (Konståkning ) och man vill nog inte att konståkning skall bli cirkusakrobatik.

Utveckling av utrustning

Jag kan inte se någon möjlighet här, men man vet aldrig.

Önskvärt?

Man kan fråga sig om kvintupelhopp är önskvärda. Det är risk att man förlorar elegansen i konståkningen. Och vi amatörer som tittar på har inte en chans att räkna antalet rotationer.
/Peter E

Nyckelord: *idrottsfysik [42];

1 https://sverigesradio.se/artikel/6664456
2 https://www.theglobeandmail.com/sports/olympics/quad-is-now-a-norm-in-mens-figure-skating---will-the-quint-be-next/article16849396/

Kan en flygplansvinge alstra någon lyftkraft i färdriktningen?
/Anders N, Kristinebegskolan, Åmål

Svar:
Om man ställer en flygplansvinge vertikalt blir den ju i princip ett segel. Det går ju att segla snett emot vinden (se figuren nedan), så man har en kraftkomponent i färdriktningen. Det räcker emellertid inte att vrida en vinge för att åstadkomma en segelbåt. En segelbåt har en köl som verkar mot vattnet och därmed hindrar en drift i sidled.

Hur kan man segla 90 grader i förhållande till vinden? Man ställer seglet i c:a 45 grader i förhållande till vinden. Vinden kommer då att avlänkas mot aktern. Kraften som böjer av vinden måste ha en motkraft (Newtons tredje lag, fråga 15642 ) som verkar i framåtriktningen. Så det är huvudsakligen två komponenter som driver segelbåten framåt: seglet och kölen.

Den framåtriktade kraften accelererar båten framåt, men med ökande hastighet får man ett ökande motstånd på skrovet (engelska drag). Sluthastigheten bestäms av balansen mellan den framåtriktade kraften och motståndet. Vindhastigheten är inte en absolut gräns för hastigheten om bara skrovet är konstruerat för litet motstånd. Två faktorer som påverkar hastigheten positivt är långsmal form och om skrovet kan lyfta och vattenplana så att bogvågen minimeras.

En segelbåt kan inte färdas i rak motvind eftersom det av symmetriskäl inte finns någon framåtriktad kraft på seglet. Det optimala är att färdas i 90 grader mot vinden eftersom den framåtriktade kraften är maximal. Så snart båten färdas med vinden kommer effektiva vindhastigheten minska vilket minskar hasigheten, se länk 1.

Se även länkarna nedan och fråga 8182 och 13364 .

Nyckelord: segling [5]; flygplansvinge [8]; *idrottsfysik [42];

1 http://www.real-world-physics-problems.com/physics-of-sailing.html
2 http://www.sailguide.com/forum/viewtopic.php?t=1342

Ursprunglig fråga:
Hej! Vi gör vårt gymnasiearbete i fysik och tittar på energiöverföringar i ett golfslag. Mer specifikt undersöker vi själva träffen mellan boll och klubba. Vi har gjort en videoanalys och därigenom fått ut hastigheter för: boll, samt klubba före och efter träff. Vi är dock lite osäkra på hur vi ska räkna med massan för klubban. Ska man göra antagandet att all klubbans massa ligger i klubbhuvudet, eller ska man enbart räkna med klubbhuvudets massa, eller ska man försöka ställa upp en mer avancerad modell? Om inte, hur stort skulle felet tänkas bli, och varför?

Tack på förhand! Vänliga hälsningar, Emma och Melker
/Melker H, Viktor Rydberg Odenplan, Stockholm

Svar:
Emma och Melker! Fysiken bakom golf är mycket komplicerad, men man kan förstå en hel del genom att förenkla problemen. Teorin innehåller ofta fria parametrar som anpassas till mätdata.

I boken The Physics of Golf av Theodore P Jorgensen görs en ganska omfattande analys, men det är inte helt lätt att förstå detaljerna.

Låt oss titta på ert problem som är det enklaste: en central stöt mellan ett klubbhuvud med massan M och en boll med massan m. Klubbhuvudet har 0 graders loft, så vi har inget spinn. Precis före stöten är klubbhuvudets hastighet V. Efter stöten är klubbhuvudets hastighet u och bollens hastighet är v. Vi antar att stöten är elastisk så att vi inte har några förluster som t.ex. inre friktion pga bollens eller klubbhuvudets deformering. Vid stöten måste vi bevara rörelsemängd och kinetisk energi:

MV = Mu + mv (1)

MV²/2 = Mu²/2 + mv²/2 (2)

Om vi eliminerar u (klubbhuvudets hastighet efter stöten) i (2) med hjälp av (1) får vi för bollens utgånghastighet

v = 2MV/(m+M) = 2V/(m/M + 1) (3)

(I länk 1 finns mer detaljer av härledningen med andra beteckningar.)

Mycket av vad som följer är från kapitel 9 i The Physics of Golf (se ovan).

Om m är mycket mindre än M får vi att v=2V. Detta är alltså den teoretiskt högsta möjliga hastigheten för bollen. Om m=M får vi att v=V (klubbhuvudet är i vila efter stöten). Bollens utgångshastighet är alltså proportionell mot klubbhuvudets hastighet: v = k*V. Konstanten k beror av deformationsförluster (se studskoefficient i fråga 20384 ) och klubbans loft.

Typiska värden för k är 1.46, 1.30 och 1.12 för driver, järnfemma och järnnia, respektive. Klubbhastigheten för en bra spelare är ungefär 45 m/s vilket ger en bollhastighet med driver av 1.46*45=66 m/s. Detta ger en slaglängd på c:a 225 m.

Med ett flexibelt skaft kan man som en hygglig approximation anta att klubbhuvudet vid bollträffen uppför sig som en fri kropp.

Ju större loft en klubba har desto mer spinn får bollen efter träffen. Spinnet ger genom dimplarna och Magnus-effekten en lyftkraft och turbulens som minskar luftmotståndet (se fråga 14113 ). Detta gör att bollen flyger längre.

Spinnet kostar emellertid genom att k blir mindre (se ovan). Detta reflekterar faktumet att en del av den överförda energin går till bollens rotationsenergi.

Parentes: Uttrycket v=2V för ett tungt klubbhuvud kan vi få med ett enklare resonemang. Vid en fullständigt elastisk kollision mellan två objekt bevaras den relativa hastigheten. I ovanstående exempel är relativa hastigheten V (klubbhuvudets hastighet). Efter stöten fortsätter klubbhuvudet med hastigheten V och bollen har hastigheten V i förhållande till klubbhuvudet. Bollens hastighet i förhållande till marken är då v=V+V=2V.

Här är fler frågor som behandlar golf: golfboll . Se även länk 2.
/Peter E

Nyckelord: golfboll [15]; elastisk stöt [12]; *idrottsfysik [42];

1 http://hyperphysics.phy-astr.gsu.edu/hbase/elacol2.html#c2
2 http://raypenner.com/golf-physics.pdf

1) Hur stort är luftmotståndet?

2) Vi antar att luftmotståndet kan skrivas F= kv^2 där v är gränsfarten och k är vindfångsfaktorn. Räkna ut k.

3) Använd friktionstalet och k-värdet från d-uppgiften. Räkna ut toppfarten(gränsfarten) för två andra skidåkare som väger 100 kg respektive 60 kg. Vad betyder skidåkarens massa för toppfarten?
/Max N, Karolinska gymnasiet, Örebro

Svar:
Som vi har sagt många gånger så svarar vi inte på räkneuppgifter om de inte är av allmänt intresse, se fråga 17395 .

Har du försökt lösa problemet? (1) borde du rimligen klara genom att dela upp tyngden mg i komponenter längs och vinkelrätt mot backen.

(2) Luftmotståndskonstanten räknas ut från den resulterande kraften (tyngdkraftskomponenten parallellt med backen - friktionskraften).

(3) d-uppgiften? Om det menas (1) så är problemet helt orealistigt eftersom massan måste ingå i värdet på k. Som det formuleras är luftmotståndet samma för alla åkare, men ytan bör ju rimligen bero av massan. Det vore bättre att använda uttrycket i fråga 18144 för luftmotståndet.

Vi kan göra en uppskattning av sluthastigheten med uttrycket från fråga 20012 med den givna sluthastigheten 36.1 m/s:

V_t ~ m^1/6

V_t = 36.1*(60/80)^1/6 = 34.4 m/s

V_t = 36.1*(100/80)^1/6 = 37.5 m/s
/Peter E

Nyckelord: luftmotstånd [11]; *idrottsfysik [42];

Ursprunglig fråga:
Fråga angående ”869”, där ni diskuterar massans betydelse för en störtloppsåkare. I svaret påstås att en tyngre åkare får en högre hastighet med följande resonemang:

”Kraften som drar skidåkaren nedåt är ju proportionell mot massan, medan kraften som bromsar (luftmotståndet) är proportionell mot ytan. Vi får allstå en större kraft för den tyngre skidåkaren, medan luftmotståndet inte ökar lika mycket. Så om allt annat är lika så har en tyngre åkare en fördel.”

Jag förstår inte resonemanget kring hur en större kraft ger en större hastighet...

MITT RESONEMANG: Hänvisningen är således till Newtons andra lag: F = ma. Ett större föremål får ju en större kraft. Men: Detta är i mina ögon inte samma sak som att föremålet får en högre hastighet - det är ju en större massa som ska accelereras. Galileis lag ger att två föremål som faller från samma höjd faller lika fort oberoende av vikt givet att fritt fall föreligger. Detta trots att det tyngre föremålet påverkas av en större kraft. I vardagen har vi inte fritt fall, utan ett motstånd. Men det blir inte med nödvändighet mindre om massan ökar. På motsvarande sätt menar jag att skidåkaren kommer att omsätta lägesenergi i rörelseenergi: mgh = 0,5mv^2, dvs massan spelar ingen roll om luftmotståndet och friktionen från underlaget försummas (givet att åkaren inte ”stakar”). Enligt det resonemanget att en tyngre åkare skulle vara snabbare, så måste det innebära att han får ett mindre motstånd. Jag har svårt att se hur luftmotståndet skulle minska med massan (vilket inte heller påstås). Återstår att den tyngre åkaren skulle ha mindre friktion, trots att friktionen är proportionell mot normalkraften (som beror av massan). Det skulle möjligen kunna vara sant om åkaren med sin större massa trycker ner snön och därmed påverkar friktionstalet till sin fördel (vilket är tveksamt i en välpreparerad backe).

Min förklaring till att en tyngre åkare skulle kunna ha en fördel är följande: Utförsåkning är en krävande sport. Det är jobbigt att krypa ihop i störtloppsställning. Det krävs stora krafter för att kunna hålla emot i svängarna. Det gynnar en fysiskt vältränad person med stor muskelmassa. Att lägga på sig muskelmassa ger en större vikt. Kraftfullheten som åkare ger en större effekt än den uppbromsande friktionen från en ökad massa, varför en tyngre åkare borde ha fördel (förutsatt att massan sitter på rätt ställe).
/Philip L

Svar:
Nej, resonemanget i fråga 869 är korrekt och, tycker jag, tydligt. Du antar att luftmotståndet kan försummas. Det är tvärtom så att luftmotståndet är den dominerande bromsande kraften vid hög hastighet (se länk 1, s 350). Du kan se det vid en störloppstävling. Om en åkare har dålig balans måste hon/han resa sig lite för att återfå balansen. Man ser tydligt på mellantiderna att den sämre aerodynamiken medför att farten minskar.

Det är klart att skidåkarens vikt bara är en parameter som bestämmer resultatet. God teknik och styrka att hålla emot g-krafter (se fråga 15970 ) är självklart mycket viktiga -- Lindsey Vonn är relativt stor för en tjej (75 kg, 178 cm lång) men det är säkert den utmärkta tekniken som gör henne så överlägsen! Intressant är också att Anja Pärsson föredragit att vara lättare, med det var för att bli bättre i slalom, se länk 2.

Här är ett annorlunda resonemang som leder till samma slutsats:

Om vi antar att den dominerande bromsande kraften är luftmotståndet kan man härleda ett uttryck för sluthastigheten enligt nedanstående bild från fråga 15385 . Om vi stryker alla konstanter och låter ~ betyda proportionellt mot, så får vi sluthastigheten

V_t ~ sqrt(m/A) ~ sqrt(r³/r²) = sqrt(r)

I termer av massan m får vi eftersom m ~ r³:

V_t ~ sqrt(r) ~ (m^1/3)^1/2 = m^1/6

Sluthastigheten ökar alltså som sjätte roten ur massan.

Se även fråga 18144 .

Nyckelord: *idrottsfysik [42]; luftmotstånd [11];

1 http://cdn.intechopen.com/pdfs-wm/16679.pdf
2 http://www.aftonbladet.se/sportbladet/vintersport/alpint/article12733366.ab

Jag utövar Airsoftskytte. Min fråga är om det går att beräkna kulans energi i en viss punkt i dess bana innan den faller till marken? Vi vill utreda hur kulans vikt kontra utgångshastighet påverkar kulan i dess bana samt vilken kraft den färdas med x meter från starläget.

Följande förutsättningar måste gälla: Kulan har backspinn när den lämnar mynningen Luftmotstånd måste vara med i beräkningen Kulan har formen av ett klot Kulans form är oförändrad under hela färden

Går detta att beräkna med gällande förutsättningar
/Georgi S, FD Chalmerist, Gbg

Svar:
Nej, det är mycket komplicerat speciellt om man skall ta hänsyn till spinn. Ett liknande problem är hur en golfboll flyger. För golfbollen finns dyra avancerade mätinstrument med sofistikerad programvara som mäter rörelsen parametriserar flykten med mycket goda resultat (t.ex. Trackman, länk 1). Något liknande finns, såvitt jag vet, inte för Airsoft.

Det finns en del dokumentation om Airsoft i Wikipedia: Airsoft .

I stycket Airsoft_pellets#Pellet_ballistics finns ett förenklat uttryck för luftmotståndet.

Jag kan emellertid inte förstå hur man får backspinn på kulan. Möjligen kan den, om den delvis rullar ut genom pipan, få lite toppspinn.
/Peter E

Nyckelord: luftmotstånd [11]; *idrottsfysik [42];

1 http://trackmangolf.com/

Svar:
Hej Jens! Du refererar till fråga 18591 . Det finns även en besläktad fråga om handboll, se 14870 .

Det är fysikaliskt omöjligt att pilens hastighet kan öka om det inte finns en extern kraft (se Newtons första rörelselag, fråga 17040 ). Den externa kraften är snarare luftmotståndet som i stället bromsar upp pilen.

Om pilen verkligen penetrerar tavlan mer på 20 meters avstånd än på 1 meters avstånd måste det bero på något annat än hastigheten. Jag har konsulterat en person (tackar!) som har 30 års erfarenhet av bågskytte, och han hävdar bestämt att det är tvärtom: penetrationen av tavlan minskar med skjutavståndet.

Nedanstående video visar emellertid att pilens flykt är mer komplicerad än man skulle tro. Pilen slingrar sig fram som en orm. Kan det vara denna effekt som ger mindre penetration i tavlan på korta avstånd?

Vad som skulle behövas för att etablera fenomenet är väldokumenterade kvantitativa mätninger.
/Peter E

Nyckelord: *idrottsfysik [42];

Svar:
Sluthastigheten bestäms till en stor del av luftmotståndet. Luftmotståndet är mycket mindre för speed skiing än normal sky diving. Se en mycket informativ artikel från Wikipedia: Speed_skiing .
/Peter E

Nyckelord: *idrottsfysik [42]; fallrörelse [31];

Svar:
Alla sporter där tyngdkraften är begränsande och som inte beror av luftens lyftkraft. Ett problem är förstås att man måste ha en stor klumpig rymddräkt som hindrar rörelser.

Tyngdkraften på månen är 1/6 av jordens. Så i t.ex. kulstötning bör det vara lätt att slå världsrekordet från jorden. Längdhopp går också ganska bra.

Det finns ju ingen atmosfär på månen, så diskuskastning går inte så bra eftersom detta till en del tar hjälp av luftens lyftkraft (som ett flygplan). Golf har faktiskt prövats på månen se fråga 12882 .
/Peter E

Nyckelord: *idrottsfysik [42];

Svar:
Jag tror inte att det lite speciella uttrycket har ett namn. Göran! Mätmetoden utvecklades av Edward Stimpson 1935, se Stimpmeter . Det är korrekt att det urspungliga uttrycket såg ut som du skriver. Det är emellertid i praktiken mycket liten skillnad på originaluttrycket och det enkla medelvärdet (x+y)/2. United States Golf Association, som tillsammans med Royal and Ancient Golf Club of St Andrews bestämmer om golfens regler, rekomenderar faktiskt numera att man använder det enkla medelvärdet, se länk 1.

PS. Jag blev först lite orolig. En golffråga från golforaklet Göran Z! Men det var inte Göran_Zachrisson !
/Peter E

Nyckelord: *idrottsfysik [42];

1 http://www.usga.org/course_care/articles/management/greens/Stimpmeter-Instruction-Booklet/

Ursprunglig fråga:
Vid backhoppning borde inte massan spela någon roll för hastigheten vid själva uthoppet (väl?). Varför är det då en "trend" för backhoppare att de ska var så små som möjligt? Är det för att minska luftmotståndet?
/Sara L, Fredrikabremer gymnasiet, Haninge

Svar:
Sara! Intressant fråga, speciellt med tanke på tidigare svar om störtlopp! Jo, massan har betydelse för uthoppshastigheten. Se fråga 869 där det visas att hastigheten för en tyngre störtloppsåkare är större än för en mindre.

Hur kan det då komma sig att de bästa backhopparna ofta är små och lätta? En antydan får man om man jämför dräkterna. En störtloppsåkare har en tätsittande dräkt för att minimera luftmotståndet, medan en backhoppare har breda skidor och en dräkt som är "fem nummer för stor". Det är alltså inte farten i backen som bestämmer hopplängden utan förmågan att sväva långt i luften. För detta behöver man liten vikt och stor yta. Den stora ytan åstadkommer man dels med en väl tilltagen dräkt och dels med den s.k. V-stilen (Jan Boklöv, V-style ) som ger mer lyftkraft på kroppen eftersom den inte skuggas av skidorna - större "vinge" ger större lyftkraft. Hopplängden bestäms alltså till en stor del av aerodynamiken i luften.

En annan aspekt som gör farten i backen mindre utslagsgivande är att en stor del av uthoppshastigheten kommer från ett väl tajmat uthopp. Det är här och i förmågan att hålla kropp och skidor i en effektiv vinkel som skiljer bra hoppare från mindre bra.

Se vidare Backhoppning och Ski_jumping . Bilden nedan är från Wikimedia Commons.

/*fa2010_4

Nyckelord: *idrottsfysik [42];

Ursprunglig fråga:
Hej! Skulle vilja veta vad som händer när man "curlar" i curling? Vad är det som gör att stenen glider bättre då?
/Hannes H, Alströmergymnasiet, Alingsås

Svar:
Hannes! Intressant och aktuell fråga med tanke på lag Anette Norbergs insats i OS i Vancouver. Detaljerna för varför stenen "curlar" (avlänkas åt höger eller vänster i förhållande till den ursprungliga riktningen) är komplicerade och även kontroversiella. Vi behandlar detta i avsnittet mot slutet av svaret. Först en video om curling:

Vissa saker är man emellertid helt överens om:

1 Sopandet framför stenen skapar genom friktion värme som smälter isen och ger ett tunnt lager vatten. Detta minskar friktionen mellan stenen och isen.

2 Minskningen i friktion genom sopning medför dels att stenen går längre sträcka för en viss utgångshastighet och dels att den curlar (svänger) mindre.

3 Stenens curlande orsakas av friktionen mot isen och stenens rotation. Observera att man alltid sätter lite rotation på stenen: moturs om man vill att den curlar åt vänster och medurs om man vill ha en högerböj.

Till skillnad från andra sporter (t.ex. golf, bowling, skytte) kan man alltså påverka projektilens rörelse efter det att man släppt iväg den. Svårigheten är att man alltså får två effekter när man sopar: längre bana och mindre curl, och man måste besluta om en optimal kompromiss mellan effekterna.

SVTs kommentatorer vid OS-sändningarna från Vancouver spekulerade om vad resultatet skulle bli om det svenska damlaget skulle spela mot det svenska herrlaget. Man kom fram till att herrarna antagligen skulle vinna, men förklarade inte varför. Jag tror också herrarna skulle vinna helt enkelt för att de är tyngre och starkare, och kan på så sätt kontrollera stenen mer. Om man tittar på statistik för absoluta topp-curlare så har män c:a 90% och kvinnor c:a 80% lyckade stenar (slag).

Detaljerad förklaring till att stenen curlar

Låt oss börja med att göra ett enkelt experiment som du kan göra hemma. Ta ett köksglas (inte mormors finaste glas!) och leta upp ett jämnt, plant underlag, t.ex. en köksbänk. Vänd glaset upp-och-ner och skjut det längs bänken samtidigt som du sätter rotation på glaset, se vänstra bilden i nedanstående figur från Curling Science . Om du som i figuren roterar glaset medurs, så kommer glaset att avlänkas till vänster. Detta resultat är mycket förvånande för en curlare eftersom en curlingsten skulle avlänkas åt motsatt håll, se den högra bilden.

Varför reagerar glaset och curlingstenen olika på rotationen? Låt oss börja med att förklara varför glaset rör sig åt vänster. När glaset glider över bänken bromsas det up av en friktionskraft riktad rakt bakåt. Eftersom glasets tyngdpunkt ligger över bänkens plan, så kommer det att utsättas för ett vridmoment riktat bakåt. Trycket på framkanten av glaset blir då högre än trycket på bakkanten. Detta är samma effekt som att en bromsande bil får nosen nertryckt och en accelererande bil får nosen lyft. Eftersom glaset roterar får vi även en friktionskraft riktad åt vänster (friktionskraften är alltid motriktad rörelsen) i glasets framkant och en friktionskraft riktad åt höger i glasets bakkant. Eftersom normalkraften F_n enligt ovan är större i framkanten än i bakkanten blir friktionen större (se nedanstående formel), och vi kommer att få en nettokraft riktad åt vänster.

Varför uppför sig curlingsten annorlunda än glaset? För det första bör man veta att bottenytan på en curlingsten inte är plan, utan den har en skålformad fördjupning i mitten. Anläggningsytan mot isen är alltså en smal ring precis som för det upp-och-nervända glaset.

Skillnaden är att is smälter om den utsätts för högt tryck, se fasdiagrammet i fråga 12715 . Detta är skälet till att en kälke eller skridskor glider så bra på is - friktionen minskas genom ett tunnt vattenskikt. Precis som glaset utsätts stenen för en större normalkraft i framändan än i bakändan. I fallet curlingsten orsakar det högre trycket i framändan att friktionskoefficienten m minskar. Friktionskraften är ju

F = mF_n (1)

Eftersom minskningen i friktionskoefficienten är större än ökningen i normalkraften kommer friktionskraften att bli mindre i framändan. Stenen kommer då att i stället böjas av åt höger.

Eftersom förklaringen bygger på att en del is smälts, så bör det ha betydelse vilken temperatur isen har. Om isens temperatur är mycket låg borde man vänta sig att den har svårare att smälta och att friktionen skulle bli större. I länk 1 sägs det om Scotts (Robert_Falcon_Scott ) sydpolsexpedition:

Another key factor when considering the slipperiness of ice is temperature. Captain Scott noted during his Antarctic travels that once the temperature fell below -35 degrees C it become incredibly hard to pull sleds through the snow. This was because the heat produced by the friction between sled and snow was not enough to warm the ice to its melting point (0 degrees C) so no lubricating melt water was produced. Scott and his companions may as well have been pulling their sleds through sand. The closer the temperature of the ice is to its melting point the more melt lubricant is produced by sliding and the more slippery ice becomes.

I What Puts the Curl in a Curling Stone? finns ovanstående förklaring till curlande och referenser till fyra vetenskapliga artiklar från Canadian Journal of Physics om olika aspekter på curling. The motion of curling rocks: Experimental investigation and semi-phenomenological description är en senare artikel av samma författare. I den visas tydligt (men ganska svårgenomträngligt) att ovanstående modell är i stort sett korrekt även om vissa detaljer är oklara. Speciellt gäller detta hur stenen växelverkar med underlaget: växelverkar den med en fix isskiva eller med det rörliga vattnet under stenen? En annan effekt som är svår att förklara är att storleken av curl är i stort sett oberoende av stenens rotationshastighet. Intuitivt väntar man sig att en sten som roterar snabbare curlar mer.

I artikeln Comment on the motion of a curling rock framförs en annan modell där inte "våt friktion" (minskande friktionskoefficient) utan "torr friktion" (formel 1 ovan med konstant friktionskoefficient) används. Artikeln är emellertid inte av god kvalité, och slutsatserna är dubiösa.

Tester av modellerna

Det vore intressant att testa hur glaset uppför sig på is. Är det någon som har tillgång till mycket jämn is skulle jag vara tacksam om ni ville kummunicera era observationer till mig.

Ett annat experiment som är svårare att åstadkomma är att be ismakarna skruva upp kylningen till max. Skulle det gå att få ner temperaturen så mycket att man inte får någon smältning? Om det går skulle man få några mycket förvånade curlare: stenarna skulle bli mycket korta och curla åt fel håll !

Sopforskning

Sopandet är uppenbarligen en mycket viktig del av curling eftersom detta är lagets möjlighet att påverka stenens bana sedan den släppts. Curling, Olympic training and ice friction fundamentals är ett anslag till några forskare för att förbättra chanserna för det brittiska damlandslaget att försvara sitt guld från 2002 i Turin 2006. Tydligen räckte inte pengarna, för som känt så vann ju lag Norberg!

Vidare studier

Det finns som synes mycket i curling som är av fysikaliskt intresse, och då har vi inte tagit upp kollisioner mellan stenar och bevarandet av rörelsemängd och rörelseenergi.

För mer om curling se Wikipedia-artiklarna på engelska (Curling ) och på svenska (Curling ). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games . Länk 2 ger en alternativ förklaring.

Nyckelord: friktion [53]; *idrottsfysik [42];

1 http://www.research.ed.ac.uk/portal/en/projects/friction-on-icea-thermographic-analysis-of-surface-temperature(b3e37385-72c6-41bb-af3f-3440d39dcad2).html
2 http://www.forskning.se/nyheterfakta/nyheter/pressmeddelanden/curlingstenensexaktarorelserkartlagda.html

Svar:
Gunnar! Det är två saker som bestämmer hastigheten: friktionsmotståndet och hur mycket framåtriktad kraft man kan åstadkomma. Det gäller alltså att hitta ett optimalt tillstånd. Detta tillstånd beror på förutsättningarna. En motorbåt går snabbast om den planar, men det är om propellern ligger under vattenytan. Om propellern suttit direkt i skrovet, så hade den varit i luften när båten planar. Då hade framdrivningen varit nära noll.

Det är samma sak med simningen. Om man ligger alltför högt blir det bara en massa improduktivt plaskande i ytan. Det mycket effektiva fjärilsimsbentaget (tidigare kallat delfinkick) måste naturligtvis för att vara effektivt utföras med benen helt under vatten. Om man gör något liknande Anja Perssons "sälen" bromsas hastigheten snabbt upp och man måste slösa energi på att accelerera igen.

Det är naturligtvis möjligt att man kan hitta på nya sätt att simma snabbare (höjdhopp förändrades ju radikalt med införandet av den till synes aviga Fosbury floppen). Det finns emellertid mycket detaljerade regler vad man får göra i de olika simsätten (utom frisim), så variationerna måste även tillåtas av reglerna.
/Peter E

Nyckelord: *idrottsfysik [42];

Svar:
Golfbollen har högst hastighet just när den lämnat klubbhuvudet. Även om det kan finnas lite komressionsenergi i bollen, så finns det ingen mekanism för att överföra denna till ökad fart på bollen. Energin blir till värmeenergi genom friktion.

Teoretiskt kan man få en liten effekt från golfbollens rotation: rotationen ger en lyftkraft (se fråga 14113 nedan) som får bollen att gå högre. I fallet ner mot marken accelererar den naturligtvis, men hastigheten är ändå lägre än utgångshastiheten vid utslaget.
/Peter E

Se även fråga 14113

Nyckelord: *idrottsfysik [42]; golfboll [15];

Tack i förhand Mvh Hanna
/Hanna P, Kunskapsgymnasiet, Göteborg

Svar:
Hej Hanna! Vi är inga experter på cykelkonstruktion, men vi kan väl spekulera lite!

Det man vill optimera i en tävlingscykel är i första hand luftmotståndet och i andra hand cykelns totala vikt.

- Man vill ha ett elastiskt material som inte är alltför tungt. Kombinationen gummi-övertryckluft är uppenbarligen mycket bra.

- Som ett V med stång på toppen. För tävlingscyklar har även damvarianten en fullständig triangel. Detta är av hållafasthetsskäl - triangeln är mycket stabil och kräver lite vikt för mycket hållfasthet. En klassisk damcykel med öppning framför sadeln är hållfasthetsmässigt en katastrofalt dålig konstruktion.

- Ja, man vill definitivt ha smala hjul pga luftmotståndet.

Se vidare en mycket fyllig artikel i Wikipedia: Bicycle . Även den svenska artiken, Cykel , är bra.
/Peter E

Nyckelord: *idrottsfysik [42];

Svar:
Henrik! De uppgifter du givit räcker inte för att räkna ut svaret. Man måste göra fler antaganden. För det första antar vi att överarmen och underarmen är låsta i en riktning. Handen med bollen beskriver då en cirkelbana med radien 28+27=55 cm = 0.55 m.

Vidare får vi anta att accelerationen a är konstant. Sluthastigheten v_max är 130 km/h = 36 m/s (klart rimligt antagande, se länk 1). Medelhastigheten i cirkelrörelsen är, eftersom accelerationen är konstant, lika med v_max/2 (börjar på 0 slutar på v_max).

Om vi antar att armen roterar ett halvt varv, så blir sträckan som bollen färdas

s = p*0.55 = 1.73 m

Från s=v*t kan vi räkna ut tiden t för rörelsen:

t = s/v = 1.73/(36/2) = 0.096 s

från v_max = a*t kan vi räkna ut accelerationen:

a = v_max/t = 36/0.096 = 375 m/s²

Från F=m*a kan vi slutligen räka ut kraften

F = 0.149*375 = 55.9 N

Detta motsvarar en kraft på c:a 6 kp, vilket låter rimligt.

Ovanstående räkningar är emellertid inte särskilt realistiska, det finns många faktorer som gör problemet mycket komplext, t.ex.:

1 Armens massa är definitivt inte försumbar om man vill beräka den totala kraften som krävs (vi har bara räknat på kraften som påverkar bollen).
2 Handleden är säkert viktig, det är den i alla kastsporter och i golf.
3 Antagandet om konstant acceleration är antagligen inte särskilt realistiskt - antagligen byggs accelerationen upp för att bli maximal mot slutet.

Detta är ett typiskt exempel på att räkna på sportprestationer: problemen är mycket komplexa och man kan i bästa fall få en uppfattning om hur prestationen påverkas av olika parametrar.
/Peter E

Nyckelord: *idrottsfysik [42];

1 http://hypertextbook.com/facts/2000/LoriGrabel.shtml

Ursprunglig fråga:
Hej! Jag håller på och läser in kursen Fysik B och har problem med den matematiska rörelsebeskrivningen. I ett exempel som anges i kursboken är en matematisk modell över en 100-meterslöpares startförlopp:

v=10t-2.5t² samtidigt som t är mellan 0 och 2 sekunder (1)

Fråga: Hur långt har löparen enligt modellen kommit efter 2 sekunder?

I lösningen som anges börjar man med att utgå från regeln: ds/dt=v. Sedan anges, att s får bestämmas genom att göra en "primitiv funktion" till v, enligt:

s=5t²-2.5t³/3+C, där konstanten C sätts till 0 så att s=0 då t=0 (2)

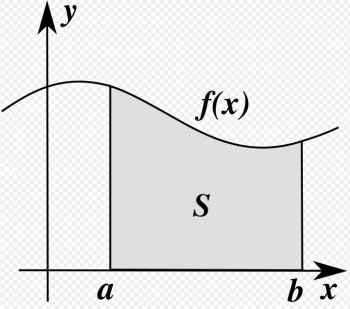
Mitt problem är att jag inte alls förstår hur denna "primitiva funktion" till v har bestämts. Hur får man stegvis fram denna funktion?? Hemskt tacksam för svar!
/Susanna A, Stockholm

Svar:
Susanna! Låt oss först beräkna accelerationen a = dv/dt. Hastigheten v ges av din ekvation (1). Derivatan av v med avseende på tiden t blir då

a = dv/dt = 10-5t

Anledningen till att accelerationen skrivs så här är ju att allteftersom löparens hastighet ökar, så måste accelerationen minska¹. Vi kan se att accelerationen enligt ovanstående modell är 0 vid t=2s. Då har löparen alltså uppnått sin sluthastighet. Om vi sätter in t=2s i (1) får vi slut(max)hastigheten 10 m/s.

Definitionen på hastighet är v=ds/dt. Hastigheten är alltså tidsderivatan vid en viss tidpunkt av den tillryggalagda sträckan. Se det så här: på den lilla tiden dt rör sig löparen sträckan ds. Hastighet är sträcka per tidsenhet alltså ds/dt.

Om vi våldför oss lite på matematiken kan vi se att ds=v*dt. Hastigheten v ges ju som funktion av t av (1). Vi kan då beräkna v for en massa värden från 0 till 2s och multiplicera med dt. Dessa ds kan vi sedan summera för att få den sträcka löparen tillryggalagt.

Matematiken bakom ovanstående kallas Infinitesimalkalkyl och utvecklades av Newton och Leibniz på 1600-talet (se Calculus och fråga 16084 nedan). Formellt är ds/dt något som kallas derivata. För att beräkna s från funktionen ds/dt måste vi integrera. Det finns massor med regler för derivering och integration (som man får lära sig i matematiken), men det viktiga i detta sammanhang är att integration är omvändningen till derivering. Så om vi integrerar ds/dt med avseende på tiden så får vi sträckan s.

Bilden nedan från Wikimedia Commons visar att integralen helt enkelt är ytan S under en funktion f(x). Integralen är alltså en yta, och räknas ut som en oändlig summa av pyttesmala rektanglar.

Hur får man då fram funktionen (2) från (1)? Ja, man måste kunna lite integreringsregler. Oftast är det emellertid enklare att derivera än att integrera, så låt oss kontrollera om (1) är derivatan av (2):

(d/dt)(5t²-2.5t³/3+C) = 10t-2.5t²

vilket alltså stämmer bra.

Det är naturligtvis måttligt intressant att beräkna hur en hundrameterslöpare spinger, men exemplet vill visa hur man i fysiken arbetar med matematiska modeller som sedan kan jämföras med verkligheten. Här är till sist en tabell med värden på a, v och s beräknade med ovanstående uttryck och med antagandet att löparen från 2 sekunder och framåt har den konstanta hastigheten 10 m/s.

  t     a     v      s
-------------------------
  0    10     0      0
  1     5    7.5    4.2
  2     0    10    13.3 
  3     0    10    23.3
  4     0    10    33.3
  5     0    10    43.3
  6     0    10    53.3 
  7     0    10    63.3
  8     0    10    73.3
  9     0    10    83.3
 10     0    10    93.3
 11     0    10   103.3

Hoppas detta hjälpte dig något!

¹ Till skillnad från en raket som accelererar snabbare och snabbare. Skillnaden beror på att för raketen är den största delen av massan bränsle, och detta försvinner ju efter hand som raketen accelererar.

Se även fråga 16084

Nyckelord: fysikalisk modell [12]; *idrottsfysik [42];

Ursprunglig fråga:
Hej! Vilka krafter utsätts en utförsåkare för (g-kraft)? :)
/Sara B, Nya Läroverket, Luleå

Svar:
Sara! Tyngdkraften rakt nedåt, normalkraften vinkelrätt uppåt från backen, friktionkraften bakåt längst skidan och till slut luftmotståndet i en riktning motsatt färdriktningen.

Det var ett svar som frågan är formulerad. Men du menade antagligen vilken g-kraft en skidåkare kan utsättas för när hon svänger. Accelerationen a i en cirkelbana med radien r är

a = F/m = v²/r

där v är hastigheten. Låt oss anta hastigheten för en störtloppsåkare är 100 km/tim och krökningsradien r 50 m. Hastigheten 100 km/tim är 100000/3600 = 28 m/s, så vi får

a = 28²/50 = 15.68 m/s² = (15.68/9.81) g = 1.60 g.

Denna g-kraft är alltså riktad utåt, bort från krökningscentrum. Till denna komponent får man sedan addera tyngskraftkomponenten 1g riktad nedåt. Resultanten av dessa två blir då med hjälp av Pythagoras sats:

sqrt(1*1+1.6*1.6)g = 1.90g

Under korta perioder kan man nog tänka sig t.o.m. tvärare svängar än detta, så man kan förstå varför en störtloppsåkare är så trött efter bara ett par minuters åkning.
/Peter E

Nyckelord: bobåkning/störtlopp [4]; *idrottsfysik [42]; g-krafter [18];

Svar:
Jag är ingen expert på slalombanor och jag kan inte hitta något om detta på nätet. Vi får därför försöka fundera ut vad som händer.

Salt används ju för att smälta is och snö på vägar, se fråga 14060 . Det kan då tyckas konstigt att man använder det på en slalombana, där man definitivt inte vill ha barmark.

Man använder salt på en slalombana när underlaget är mjukt, dvs när snön är finkornig. Finkornig snö får man t.ex. från en snökanon. Tillsatsen av lite salt gör att lite av snön smälter, men fryser sedan igen (smältningen kostar energi så den orsakar en temperatursänkning) och bildar större snökristaller eller i extrema fall solid is. Man får då ett fastare underlag - till skillnad från pudersnö som är extremt mjuk och finkornig. Duktiga skidåkare föredrar en isig bana till skillnad från du och jag som ser ut som Bambi på is .

Länk 1 nedan beskriver egenskaperna hos olika salter. Fråga 15592 beskriver hur snökanoner fungerar.
/Peter E

Se även fråga 14060 och fråga 15592

Nyckelord: vatten/is [49]; iskristaller [5]; *idrottsfysik [42];

1 http://chemistry.about.com/cs/howthingswork/a/aa120703a.htm

Svar:
Lene! På varje klubba finns en s.k. "sweet spot" där det är tänkt att bollen skall hamna. "Sweet spot" ligger i linje med klubbhuvudets tyngdpunkt. Detta innebär att en träff på "sweet spot" inte förorsakar något vridmoment. Träffar du däremot t.ex. på tån (långt ut på bladet) vrids klubbhuvudet så att klubbytan pekar höger om målet (för en högerspelare). Denna vridning orsakar följande icke önskade effekter

1. Bollen går till höger
2. Bollen går kortare eftersom en del av rörelsemängden som skulle överföras till bollen går åt till att rotera klubbhuvudet

Två tips för att förbättra ditt spel är dels att träna på bollträffen och dels att hålla så löst som möjligt i klubban. Ett hårt grepp gör att du får mindre fart på klubbhuvudet.

Lycka till med golfen!
/Peter E/hcp 17.7

Nyckelord: golfboll [15]; *idrottsfysik [42];

1 http://entertainment.howstuffworks.com/golf-club.htm

Svar:
Patrik! Jag har pratat med en tävlingscyklist om detta och han påpekar att rullfriktionen för en tävlingscykel är helt försumbar i jämförelse med den dominerande effekten: luftmotståndet. Alla eventuella effekter på rullfriktionen från hjulens storlek är försumbara jämfört med höjdens påverkan på luftmotståndet. En ytterligare begränsning är att hjulen enligt reglerna måste vara lika stora bak och fram.

Den optimala storleken på hjulen beror på kroppsstorleken. Det är uppenbart att med stora hjul kommer man med normal design högt upp och orsakar stort luftmotstånd. Detta blir mindre med små hjul (cykel/cyklist-paketet mer kompakt). För lagtempo är lite mindre hjul optimalt eftersom man då kan komma närmre varandra. Man kan emellertid inte ha hur små hjul som helst: det måste finnas plats för pedalerna och ett visst avstånd mellan kroppen och pedalerna så man kan få kraft i trampandet. Små hjul är dessutom känsligare för ojämnheter i vägbanan.

Jag tror att dessa avvägningar i stort sett definierat hjulstorleken till 559 mm för mountainbike och 622 mm för en vanlig tävlingscykel. Att avvika från detta är svårt framför att för att det är svårt att få tag på hjul och däck i andra storlekar.
/Peter E

Nyckelord: friktion [53]; *idrottsfysik [42];

Svar:
Låt oss börja med att definiera ett par begrepp.

Elasticitet är ett materials benägenhet att deformeras på så sätt att den deformerande energin omvandlas till potentiell energi. Ett elastiskt material återgår på så sätt till viloläget, och energin omvandlas tillbaka till rörelseenergi.

Motsatsen är plasticitet, som innebär att den deformerande energin genom inre friktion omvandlas till värme.

Svaret på din fråga är att materialets (gummits) egenskaper ändras med temperaturen. En varm gummiboll har bättre elasticitet och förlorar därför mindre energi när den studsar. Om du kyler en gummiboll till flytande-kväve temperatur blir den stenhård och studsar inte alls. Den spricker i stället i bitar som porslin.

Om bollen är ihålig (tennisboll, squashboll) så ökar trycket (gaslagen, allmänna ) hos den inneslutna luften och elasticiteten ökar. En ouppvärmd squashboll uppför sig nästan som en klump lera (hög plasticitet) med mycket dåliga studsegenskaper, men får god elasticitet när den är uppvärmd.
/Peter E

Nyckelord: *idrottsfysik [42]; elastisk stöt [12];

Den är i stort sett klar, men den räknar inte med en del saker som jag gärna vill få med i programmet.

1: Till att börja med räknar den med att bollens skruv hela tiden är konstant vilket givitvis inte stämmer. Skruven saktas ju ner på grund av luftmotståndet, min fråga är då hur mycket saktar skruven ner och vad beror det på hur mycket skruven saktar ner, finns det någon bok eller web sida jag kan titta på eller vet ni ?

2: Det andra som jag inte har med i beräkningaran är när bollen studsar emot bordet. Vad händer då ? Jag har beräknat studs koefficienten, men jag vet inte vad som händer med bollens hastighete i det horisontella ledet eller vad som händer med dess skruv när den studsar. Vet ni någon information om detta ?
/Rickard S, Frölundagymnasiet, Askim

Svar:
Rickard! Även något så till synes enkelt som en bordtennisbolls rörelse är ganska komplext. Du måste alltså försöka göra enkla antaganden för att beskriva bollens rörelse så bra som möjligt. Jag är ingen expert på detta, så jag kan inte vara till mycket hjälp. Försök söka med Google, några länkar finns under skruvad boll .

1 Du får parametrisera problemet, dvs skriva ett uttryck med några parametrar som beskriver en effekt. Antag t.ex. att lyftkraften från underskruven är A från början. Friktionen mot luften kommer att bromsa spinnet. Lyftkraften kommer då att avta på något sätt som säkert är en komplicerad funktion av bollens hastighet, dess rotationshastighet och luftens densitet. Som en första approximation kan du anta att lyftkraften är A-B*x, där A och B är parametrar som bestäms av experiment och x är en oberoende variabel (tid, hastighet..).

2 Om bollen roterar när den träffar bordet kommer utfallsvinkeln inte att vara lika med infallsvinkeln som den är med en studs utan spinn. Vad vinkeln i själva verket blir är igen en komplicerad funktion av rotationshastigheten och friktionen. Igen, är nog det bästa att göra en enkel parametrisering och bestämma parametrarna från experiment.
/Peter E

Nyckelord: skruvad boll [10]; *idrottsfysik [42];

Svar:
Elisabeth! Det är säkert inget bra antagande att man kan bortse från luftens inverkan för en pils flykt. Om man betraktar pilens bana som en kastparabel är problemet ganska enkelt. Vi antar också att utgångsvinkeln är ganska liten:

1 Räkna ut hur lång tid det tar för pilen att nå målet.

2 Räkna ut hur mycket pilen faller vertikalt under denna tid.

1 s = v*t ger t = s/v = (90 m)/(50 m/s) = 1.8 s

2 s_v = g*t²/2 = 9.81*1.8²/2 = 15.9 m

Vinkeln blir då atan(15.9/90) = 10.0 grader. Det var en väldigt stor vinkel, men jag tror utgångshastigheten 50 m/s är lite lågt - 100 m/s bör vara mer normalt. Utgångsvinkeln blir då 4 gånger mindre - c:a 3 grader vilket låter mer rimligt. Men sedan har vi även luftens inverkan.
/Peter E

Nyckelord: kastparabel [10]; *idrottsfysik [42];

Ursprunglig fråga:
Hej! Jag hade tänkt att tillverka en golf-putter som får bollen att rulla direkt vid tillslaget. Gräs som underlag förståss. Är det fysiskt möjligt?

Om JA:
- Hur ska man göra i så fall?
- Hur ska puttern vara utformad?
- Krävs någon speciell slagteknik?

Om NEJ:
- Hur gör man för att minimera det så mycket det bara går?
- Hur ska puttern vara utformad?
- Krävs någon speciell slagteknik?

Tack för svaren!
/Joakim G, Sanda Gymnasiet, Huskvarna

Svar:
Hej Joakim! Intressant fråga till en entusiastisk golfare men dålig puttare!

Puttning är egentligen mycket enkelt: slå bollen med rätt hastighet i rätt riktning med hänsyntagande till fall på grund av greenens lutning och eventuell vind. Förutom en god teknik (som finslipas med mycket träning) är självförtroende A och O i golf: alla golfare vet att man misslyckas med de flesta slagen med en klubba man inte "tycker om".

Du har helt rätt i att det är mycket viktigt att få bollen att rulla - inte glida - så snart som möjligt. Detta gör man genom att sätta "överskruv" på bollen, dvs så att bollen roterar i samma riktning som den gör när den rullar. Detta är tvärtom mot skruven som åstadkoms med andra klubbor: klubbladets loft (lutningen mot horisontalplanet) orsakar underskruv, vilket en skicklig spelare kan utnyttja till sin fördel, se golfboll . Du vill alltså ha mycket lite loft på en putter (slagytan skall vara nästan 90 grader mot horisontalplanet), annars får du en i de flesta fall icke önskad underskruv.

Överskruven åstadkommes genom att man täffar bollen när puttern är lite "på uppgång" - bollen lite till vänster i stansen och en pendelrörelse hos klubbhuvudet som når sin lägsta punkt lite innan det träffar bollen. Det fordras lite träning för att lyckas med det varje gång.

Vilka egenskaper bör en bra putter ha?

• Det bör vara lätt att sikta
• Tydlig "sweetspot", vilket är den träffpunkt som inte orsakar rotation hos klubbhuvudet
• Lite loft (högst några få grader) så man kan åstadkomma överskruv
• Ett handtag som ger en känsla för vart klubbhuvudet pekar (ej cylindersymmetriskt)

14738

Friktionen (och därmed uppbromsningen) är större när bollen glider (och kanske hoppar) än om den rullar fint. Du får därför en mer konsistent putt med en rullande boll.

Kan man inte få överskruv med ett negativt loft på puttern? Nej, det fungerar antagligen inte eftersom man tvingar bollen nedåt in i greenen. Men kanske skulle man kunna pröva lite negativt loft? Såvitt jag vet finns inga sådana putters, och om det fungerade skulle det säkert finnas det.

En sak är i varje fall säker: om du kan konstruera en putter som gör puttningen lättare och dessutom övertyga golfare att den fungerar, så är du miljonär!

PS. Heter du verkligen Green? Då får du kalla puttern Green-putter!

PS2. Lycka till med puttertillverkningen!

Tillägg juni 2017:

Här är en putter med en speciell yta ("microhinges") som påstås ge bollen överskruv:

Se länk 1 för mer om puttning.
/Peter E

Nyckelord: golfboll [15]; *idrottsfysik [42];

1 http://golf.about.com/od/golftips/a/tips_putting.htm

Önskar ett bättre svar än ni gav. Ökar accelerationen efter en stund pga av att deformationen försvinner?
/Anna B

Svar:
Hej Anna!

När bollen väl lämnat handen påverkas den bara av en kraft: en bromsande kraft från luftmotståndet (vi kan bortse från tyngdkraften - den ökning i hastighet en höjdskillnad skulle kunna ge upphov till bör vara mycket liten). Bollen kan alltså inte öka farten, utan farten minskar. Om effekten du beskriver är verklig måste den bero på någon annan orsak är fysikaliska lagar.

Jag har diskuterat effekten med en f.d. handbollsmålvakt, och hon bekräftar helt vad du beskriver. Vad kan upplevelsen då bero på? Ja, för det första är upplevelsen av smärta komplicerad och personlig. Dessutom har det betydelse var man träffas. Låt oss se om vi kan hitta några skäl till effekten.

1 Jag tror inte att bollens deformation är orsaken. Dels för att en normal handboll är så hård att den knappast deformeras och dels eftersom min handbollskonsult säger att en nypumpad boll (som deformeras ännu mindre) gör ännu mer ont!

2 Kanske skjuter skytten inte lika hårt om målvakten är nära? Skytten kanske inte fullföljer skottrörelsen inklusive handledsrörelsen på normalt sätt, eventuellt av rädsla att skada sig genom att slå i den utrusande målvakten, av omsorg om målvakten eller rädsla att åka på en utvisning för att ha drämt till målvakten.

3 Det hårdaste skottet är ett skott som avlossas högt - ungefär i huvudhöjd. Om den som träffas är nära bör träffen ta på överkroppen, i bästa fall på armarna. Om den som träffas står längre ifrån kan det ta på känsligare ställen, t.ex. insidan av låret.

Man behöver göra kontrollerade experiment för att mäta effekten. En mekanisk kanon som skjuter ut bollen med konstant hastighet och en målvakt som är tillräckligt korkad för att utsätta sig för träffar från olika avstånd. I vilket fall som helst får man beundra handbollsmålvaktens mod att med alla delar av kroppen försöka stoppa även de hårdaste kanonskott.

Tyvärr är detta vad som går att åstadkomma med enkel fysik och utan kontrollerade experiment .
/Peter E

Nyckelord: *idrottsfysik [42];

Ursprunglig fråga:
Hej, jag har läst igenom forumet och hittat samma fråga som jag har men det fanns inget svar på frågan. Problemet är det här med att en läderboll som får en skruv medurs skruvas till vänster, och en plastboll som skruvas medurs skruvas till höger. Jag presenterade problemet för min lärare i fysik på LTH och han trodde mig först inte. (Vilket inte personen som gav svar i forumet gjorde heller) Men jag stod på mig varpå han verifierade problemet i verkligheten. Testet utfördes i en gymnasiksal där det inte fanns någon vind. Slutsatsen var att han kunde inte förklara problemet fysikaliskt! Kan du?
/Johan J, LTH, Malmö

Svar:
Hej Johan!

Nej, jag kan inte förklara problemet. Men jag tror inte heller att olika material skruvar åt olika håll. Tänk t.ex. på en golfboll och en pingisboll. Båda påverkas på samma sätt av underskruv - de påverkas av en kraft uppåt. Detta trots att de har helt olika ytor: golfbollen är knottrig vilket ger turbulent strömning och pingisbollen är slät vilket ger laminär strömning kring bollen. Dessutom finns det ju fotbollar både av plast och av läder, och jag tror en spelare skulle bli mycket förvånad om en ny boll skruvade åt fel håll .

Skruv och lyft hos roterande bollar förklaras av den s.k. Magnuseffekten som bygger på Bernoullis ekvation - högre hastighet hos luften ger lägre tryck (Bernoulli's_principle ). Se även Magnus_effect .

En helt annan effekt är skruvade kast i kricket, men där har man en asymmetri hos bollen och skruven är riktad i samma riktning som asymmetrin - en underskruvad kricketboll avviker i sidled i stället för i höjdled. Se Swing_bowling .

Se skruvad boll , golfboll och en artikel om fotbollsfysik under länk 1.

Tillägg januari 2017

Magnuseffekten är ett fysikaliskt fenomen som uppträder för roterande kroppar. Effekten innebär att en kropp som rör sig genom en fluid (en vätska eller en gas) samtidigt som den roterar accelereras vinkelrätt mot rörelseriktningen, det vill säga att rörelseriktningen "böjs av". Det är den fysikaliska kraft som gör att roterande bollar får så kallad skruv inom olika bollsporter, se Magnuseffekten och fråga 754 .

Video som visar och förklarar Magnuseffekten:

Jag kan inte, trots omfattande sökningar, hitta något väldokumenterat exempel på att materialet i bollen skulle ha någon betydelse. Strukturen på ytan påverkar storleken på Magnus-kraften (dimplarna på en golfboll ökar t.ex. effekten betydligt), men att ett alternativt material skulle ändra kraftens riktning låter inte sannolikt.

Enligt beskrivningen ovan är det plastbollen som uppför sig som väntat. En höger utsida roterar bollen medurs, vilket ger en avvikelse åt höger (den av golfaren fruktade slicen). Kan det vara så att en läderboll är lite asymmetrisk pga en söm (se cricketbollen ovan)? Problemet med denna förklaring är att skruven skulle bero på hur bollen placeras på marken.
/Peter E

Nyckelord: golfboll [15]; skruvad boll [10]; bernoullieffekten [6]; *idrottsfysik [42];

1 http://physicsworld.com/cws/article/print/1998/jun/01/the-physics-of-football

Ursprunglig fråga:
Hejsan! Jag har ett problem. En kula släpps i en kulbana som står placerad på ett bord, vid kanten. Jag har räknat fram att kulan har fått en viss teoretisk energi när den lämnar banan och den har fått en minde energi i verkligheten.

Jag kan anse att luftmotståndet och friktionen inte har någon påverkan och jag har listat ut att det har något med rotationen av kulan att göra, så min fråga är nu. Vart tar energin vägen på sin resa ned för kulbanan?

svara gärna snabbt, arbetet ska lämnas in denna veckan..
/Anna O, Birger Sjöbergymnasiet, Vänersborg

Svar:
Ditt problem är inte helt lätt, du får nöja dig med en skiss. Lösningen finns under länk 1, men där på engelska.

Vi börjar med att bortse från kulans rotation. Antag kulans massa är m och dess sluthastighet v. Då gäller enligt energiprincipen (potentiell energi på höjden h = kinetisk energi vid botten):

mgh = mv²/2

dvs

v² = 2gh

Om kulan inte glider alls kommer den att sättas i rotation. Om tyngdpunktens hastighet i detta fallet är u, kommer vinkelhastigheten w att vara u/r där r är kulans radie. (Du får detta resultat eftersom den del av kulan som rör vid kulbanan har hastigheten 0 i förhållande till banan - kom ihåg, inget glid!).

En homogen kulas tröghetsmoment ges av J = 2mr²/5 (Tröghetsmoment#Exempel ) och rotationsenergin är Jw²/2.

Vi adderar translations-kinetiska energin och rotationsenergin och får

mgh = mu²/2 + (2mr²/5)(u/r)²/2 = mu²(1/2) + mu²(1/5)

dvs

u² = (10/7)gh = 1.43gh

Detta är klart mindre än 2gh som vi fick ovan eftersom ju en del energi går till kulans rotationsenergi. Förhållandet u/v blir ungefär 0.85, alltså 15% lägre hastighet än en kula som glider perfekt och inte roterar.

Förhållandet mellan rotationsenergi och translationsenergi blir enligt ovan

(1/5)/(1/2) = 2:5.

Tillägg om puttning i golf

Golfspelare som puttar bra ser till att slå till bollen med en något uppåtgående rörelse för att bollen om möjligt skall börja rulla omedelbart. Om man slår till bollen helt centralt kommer bollen att glida ett tag på gräset. Friktionen kommer efter ett tag att få bollen att rulla, men rotationsenergin måste tas från rörelseenergin. Bollen bromsas alltså upp för att den skall kunna få rotation. Det visar sig att längden på puttarna blir mycket mer konsistent om man kan få bollen att rulla direkt vid tillslaget.

Tekniken att få överspinn på bollen direkt vid tillslaget används även t.ex. i biljard då man oftast slår till bollen ovanför ekvatorsplanet vilket får bollen att börja rulla omedelbart.

/*fa*
/Peter E

Nyckelord: tröghetsmoment [9]; lutande plan [15]; *idrottsfysik [42]; rörelseenergi [14]; golfboll [15];

1 http://modeling.asu.edu/listserv/U7_KE_rolling_ball02.pdf

Svar:
Mattias! Intressant fråga! Se även resonemanget i fråga 869 nedan, det är lite annorlunda.

Starten är mycket viktig i bob-åkning, så man vill ha åkare med bra benmuskler. Jamaica har rätt bra bobåkare inte för att det finns mycket snö utan för att de har bra sprinters.

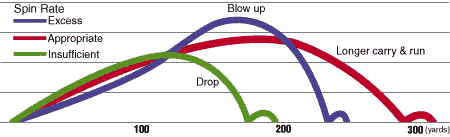
När åkarna hoppat upp i boben är det (förutom skicklighet att styra) friktion mot isen och luftmotstånd som bestämmer hastigheten. Friktionen mot marken ökar proportionellt med massan, så för den effekten har vikten ingen betydelse. Luftmotståndet är emellertid i princip oberoende av åkarnas storlek - de ligger ju gömda inne i boben - medan större vikt ger högre hastighet. Så det är en fördel att ha relativt tunga åkare. Det går emellertid inte att använda vilka klumpedunser som helst, dels eftersom dom måste kunna komma ner i boben snabbt och eftersom reglerna begränsar både bobens tomvikt och dess maxvikt, se nedanstående länk.
/Peter E

Se även fråga 869

Nyckelord: bobåkning/störtlopp [4]; *idrottsfysik [42];

1 http://www.olympic.org/uk/sports/programme/disciplines_uk.asp?DiscCode=BS

Ursprunglig fråga:
Om jag slår en golfboll med en driver kommer den att lämna peggen i med en viss hastighet och vinkel. Jag vet att klubbans hastihet är ca 190km/h och boll hastigheten ca 280 km/h utgångsvinkeln är ca 17 grader Hur räknar man ut optimal (max) höjd för en golfboll? Vilka parametrar måste man känna till?
/Roland A, Båstad

Svar:
Problemet är på grund av luftens inverkan mycket mer komplicerat. En golfboll rör sig inte alls i en kastparabel eftersom luften spelar mycket stor roll. För ett mellanjärn är banan sedd från sidan närmast hypotenusan av en rätvinklig triangel.

Spinnet och dimplarna (de små groparna) på en golfboll minskar för det första luftmotståndet (genom turbulens) och ger dessutom upphov till en lyftkraft (genom den sk Magnus-effekten). Bilden (från nedanstående länk Flight Dynamics of Golf Balls) visar bollbanan för olika spinn. Det är uppenbart viktigt all få lagom spinn på bollen!

Se Golf Ball Flight Dynamics och nedanstående länkar för olika aspekter på golfbollars rörelse.

Se även kastparabel för rörelse utan hänsyn till luftens inverkan.

Nyckelord: golfboll [15]; skruvad boll [10]; *idrottsfysik [42];

1 http://entertainment.howstuffworks.com/question37.htm
2 http://www.bettergolfcoach.com/newballflightlaws.htm

Är det inte så att det optimala är att, behålla sin fart genom att ha så lite luftmotstånd och friktion som möjligt. Det är väl ingen nackdel om du "hoppar" flyger ibland, särskilt om du inte ökat luftmotståndet och förhoppningsvis kortat av sträckan. Kan du hjälpa mig reda ut begreppen flyga, glida osv.
/Kenth L, Jakobsberg, Järfälla

Svar:
Med din begränsning är det korrekt att det går snabbare att flyga. Anledningen till att det i allmänhet anses gå långsammare om man flyger långt är nog dels att det är svårare att styra kroppen så att man har minimalt luftmotstånd om man flyger fritt i luften och dels att sträckan kan bli längre eftersom flyktbanan inte är en rät linje utan en parabelliknande kurva. Så hur bra eller dåligt det är att flyga beror på hur skicklig man är att minimera luftmotståndet i luften, och hur markprofilen ser ut, dvs vilken väg är den kortaste. Lägg märke till att de flesta störtloppsåkare reser sig upp och sträcker ut armarna för att hålla balansen när de hoppar. Se även nedanstående fråga.
/Peter E

Se även fråga 869

Nyckelord: friktion [53]; bobåkning/störtlopp [4]; *idrottsfysik [42];

Ursprunglig fråga:
Jag skriver ett arbete på gymnasienivå (Fysik B) om biomekanik med fokus på friidrottens hopp- och kastgrenar. Jag har dock kört fast vad gäller den rent teoretiska härledningen för utkastvinkeln och undrar om ni kan hjälpa mig. Den teoretiskt optimala vinkeln är 45 grader, men jag kommer inte ihåg hur härledningen ser ut.
/Anna S, NTI, Falun

Svar:
En kastparabel är den bana som ett föremål som kastas beskriver då föremålet endast påverkas av tyngdaccelerationen i ett gravitationsfält och där hastigheten i horisontalled är större än noll.

För fallet utan luftmotstånd är det lätt att bevisa att den optimala utkastvinkeln är 45^o. Vi kallar utgångsvinkeln x^o. Vi delar upp rörelsen i två komponenter: en horisontell med konstant hastighet och en vertikal med accelerationen g nedåt. Om utgångshastigheten är v blir den vertikala komponenten v sin(x) och den horisontella v cos(x).

Från den vertikala rörelsen kan vi räkna ut hur lång tid det tar för det kastade föremålet att falla från en viss höjd så att dess sluthastighet är v sin(x):

v sin(x) = gt

Eftersom fallet är spegelbilden av uppfärden (detta gäller bara om vi kan bortse från luftmotståndet) blir den totala tiden för hela kaströrelsen 2t:

2t = 2v sin(x)/g (1)

Det horisontella rörelsen sker med konstant hastighet, så kastlängden s ges av:

s = v cos(x) (2t) = v cos(x) (2v sin(x)/g)

dvs

s = 2v² sin(x) cos(x)/g = v² sin(2x)/g (2)

Maximum för sin(2x) uppnås för 2x = 90^o, dvs den optimala utkastvinkeln är 45^o.

Vi kan från ekvation 1 även räkna ut maxhöjden h:

t = v sin(x)/g

h = gt²/2 = g((v sin(x))/g)²/2

dvs

h = (v sin(x))²/2g (3)

Vi kan räkna ut h även från att kinetiska energin i x-led vid utkastögonblicket skall vara lika med den potentiella energin i vändläget (höjden h):

m(v sin(x))²/2 = mgh

dvs

h = (v sin(x))²/2g

vilket är samma uttryck som (3).

Länk 1 ger ett uttryck för den optimala vinkeln om man tar hänsyn till att utkastpunkten ligger högre än landningspunkten. Den optimala vinkeln blir då lite mindre än 45^o.

Sedan är det en annan sak att utgångsvinkeln i verkligheten för de flesta relevanta grenar (t.ex. kulstötning) är betydligt mindre än 45^o. Utgångsvinkeln varierar också mellan olika idrottare. Detta beror på fysiologi och att ansatsen sker i horisontalplanet. Det går alltså att få en högre utgångshastighet om man minskar utgångsvinkeln något. Optimeringsproblemet blir då lite mer komplicerat. Om man tar hänsyn till luftmotståndet visar det sig att den optimala vinkeln blir mindre är 45^o.
/Peter E

Nyckelord: kastparabel [10]; *idrottsfysik [42];

1 http://fysikguiden.se/kastrorelse/berakna-langd-en-kastrorelse/

Svar:
Matthias! Jag vet mycket lite om segling, men låt oss se vad man kan klura ut med hjälp av lite enkel fysik:

Vindriktning
Det är uppenbart att det inte går att segla rakt emot vinden. Att den går att segla med vinden är inte svårt att förstå. Inte heller att maxhastigheten i rak medvind är lika med vindhastigheten. I övriga riktningar kan man faktiskt ibland segla snabbare än vindhastigheten genom att utforma och rikta in segelytan optimalt.

Vid kryss (sned motvind) ger vinden en kraft på seglet och därmed via masten på båten. Denna kraft är inte nödvändigtvis riktad i vindriktningen, utan den kan ha en komponent framåt. Det är denna komponent som driver båten. Man vill naturligtvis att båten skall gå framåt, och inte driva av i sidled, dvs man måste "döda" kraftens komponent i sidled. Detta gör man med en köl och genom att göra båten långsmal. Se vidare länk 1 och 2.

Friktion
Friktionsmotståndet bromsar ju upp båten, så man vill ha så lite friktion som möjligt i framåtriktningen. Detta får man också med en långsmal båt.

Sammanfattning
Enkelt uttryckt: en snabb segelbåt skall utformas så att den har ett väl utformat segel (ger stor kraft), liten friktion i framåtriktningen och stor friktion i sidled. De senare åstadkommer man genom att göra båten långsmal.
/Peter E

Se även fråga 8182

Nyckelord: segling [5]; *idrottsfysik [42];

1 http://www.phys.unsw.edu.au/~jw/sailing.html
2 https://www.youtube.com/watch?v=b477nzyJum0

Jag har försökt att läsa in mig på detta på en sida som heter: www.rollrite.co.uk för att kunna ge ett överygande/förklarande svar för mina spelare.
/Gert F, Vännäs Gymnasium, Vännäs

Svar:
Gert! Jag kan nästan ingenting om bowling. Har provat ett par gånger, och efter ett par tur-strikes till att börja med blev det mest rännan .

Definitionen på Mass bias är: The term Mass Bias refers to the fact that the center of mass of a bowling ball is not located directly under the pin of the ball. Having a Mass Bias causes the center of gravity (CG) mark of a ball to move away from the pin, resulting in a pin-out ball. (www.morich.net/deTerminator/).

Eftersom man inte även definierar "pin" så är definitionen nästan meningslös.

Följande är helt amatörmässiga spekulationer:

Jag antar att klotet glider en stund på banan, och att friktionen får det att rotera mer efter hand. Det som bestämmer hur mycket klotet glider är i första hand friktionen (ytornas beskaffenhet) och tröghetsmomentet hos klotet. Såvitt jag förstår är massan i ett bowlingklot inte klotsymmetrist fördelad. Detta betyder att klotet får olika tröghetsmoment för olika rotationsaxlar. Klotet uppför sig allså lite olika beroende på hur det är orienterat vid utkastet. Jag misstänker att begreppet har något att göra med detta.

Det ligger alltså antagligen något i begreppet Mass bias, se emellertid nedanstående kommentarer:

Jag kan lite mer om golf, emellertid. På min "trä"-trea står det 'Calibrated technology' och 'Trajectory orientated'. Det låter naturligtvis som något man behöver för att slå långt och rakt. Det är emellertid i sammanhanget fullständiga nonsenord som bara är till för att man skall köpa klubban. Det gjorde ju jag, även om anledningen var att jag tyckte texten var så utomordentligt fånig! Klubban fungerar emellertid ganska bra, så den är kanske kalibrerad (kalibrera: anpassa eller ställa in (ngt) efter i förväg fastställda mått, NE).

Ännu ett exempel på termer och uttryck man använder (missbrukar) i speciella sammanhang: jag brukar reta bilskollärare och golfinstruktörer med att centrifugalkraften inte finns! Man kan tydligt se en ängslan i ögonen när de plötsligt förlorat något som dom byggt upp hela sitt liv på!
/Peter E

Nyckelord: centrifugalkraft [15]; *idrottsfysik [42];

Svar:
Simon! Carolina Klyft skulle vinna .

Det är en mycket komplicerad fråga eftersom så mycket spelar in. Tyngdgravitationen är 1/6 av jordens (1/6g), så om man når samma hastighet i ansatsen hoppar man 6 gånger längre. Carolina skulle alltså hoppa 6*7 = 42m. Tar man dessutom hänsyn till att det inte finns något luftmotstånd på månen så skulle hon hoppa ännu längre. I själva verket skulle ansatshastigheten bli betydligt läge i 1/6g eftersom kontakten med marken blir mycket sämre. Sedan skulle Carolina vara tvungen att bära en rymddräkt som är klumpig och tung, så det skulle ytterligare minska hopplängden.

Apollo-astronauterna som var på månen 1969-72 kom fram till att det effektivaste sättet att förflytta sig till fots var med en serie jämfota längdhopp, vilket några av dem demonstrerade med stor förtjusning.

Andra sporter som utövats på månen (av Alan Shepard, Apollo 14, Alan_Shepard#Apollo_14 , video på länk 1) är t.ex. golf. Fundera på vad är det för fel på CapCom Houstons kommentar till ett av Alan S:s försök: "That one was a bit sliced Al!"
/Peter E

Nyckelord: månfärder [7]; *idrottsfysik [42];

1 http://www.youtube.com/watch?v=KZLl3XwlAIE

Svar:
Intressant fråga! Det är inte lätt att mäta en sådan effekt, men låt mig kommentera frågan lite.

En sak är helt klar, och det är att en grupp cyklister i ett tempolopp totalt tjänar på att ligga tätt ihop i en rad. Detta gäller även fågelsträck (svanar, gäss), där fåglarna kan tjäna upp till 30% energi genom att ligga i en V-formation.

Hur den första cyklisten påverkas är svårt att mäta bl.a. eftersom den psykologiska påverkan att ha en annan cyklist i hasorna antagligen är större än den energimässiga.
/Peter E

Nyckelord: *idrottsfysik [42];

Svar:
Kastar du en elastisk boll mot en vägg med hastigheten v, studsar den tillbaka med hastigheten -v. Fartförändringen blir alltså 2v. Slår man mot en golfboll med farten v med en tung golfklubba, blir golfbollens fartändring 2v. Detta är alltså ren mekanik. Här har vi antagit helt elastiska kollisioner, vilket ju inte är alldeles sant.
/KS

Nyckelord: golfboll [15]; *idrottsfysik [42];

Ursprunglig fråga:
Jo jag undrar varför man har bredare däck vid fartsporter som t.ex. formel 1? Jag förstår att det har med väghållningen att göra men jag tycker att det borde bli en kortare bromssträcka om du har breda däck än om du har ett par smala däck som utsätts för samma normalkraft och är tillverkade i samma meterial. Stämmer inte det?

Ett annat ex. kan ju vara vem som har kortast startsträcka om förutsättningen är att det inte får spinna loss någon gång.
/Arvid M, ABB Industrigymnaium, Västerås

Svar:
Enligt den förenklade teorin för friktion som presenteras i skolfysiken så beror inte friktionskraftens storlek på kontaktytans area utan endast på normalkraftens storlek. I praktiken är det däremot så att friktionskraften ökar med arean. Breda däck ger större friktionskraft och bättre väghållning. Med dubbar blir effekten ännu större eftersom ett bredare däck hat plats för fler dubbar.

Dessutom förkortas bromssträckan och accelerationen blir bättre. Friktionstalet för kontakt gummi - asfalt är ca 1,5 för bra gummiblandningar och varma däck.

Friktionen mot asfalt är, kanske lite förvånande, större om man har omönstrade däck än om man har mönstrade. Anledningen till att däck på vanliga bilar är mönstrade är framför allt för att eventuellt vatten skall komma undan. Tänk på formel-1 bilar: vid torrt väder använder man omönstrade däck, men om det börjar regna måste man omedelbart byta annars kommer bilarna att vattenplana av banan.

Fundera: Varför har man vingar på formel 1-bilar?

Fundera: Hur fort kan man köra genom en kurva med en radie på 100 m? Antag att normalkraften är lika stor som tyngdkraften.
/GO

Nyckelord: friktion [53]; *idrottsfysik [42];

Ursprunglig fråga:
I slalomsammanhang får man av s.k. experter höra: "Det är bra att du har lagt på dej några extra kilon, för då går det ju fortare." I praktiken tycks det vara så. Men energiprincipen säger ju att massan är oväsentlig (under förutsättning att vi endast har Wp och Wk som växelverkar). Den enda förklaring jag har till fenomenet har att göra med Newtons första princip - en tröghetsfråga alltså. Den tyngre alpinisten besitter ju en större rörelsemängd. Har du några förklaringar?
/Staffan L, Tekniskt/Naturvet. Basår, Skellefteå

Svar:
Detta påstås ofta av kommentatorer, men ligger det något i det?

Det mest väsentliga (förutom skicklighet att åka skidor) är luftmotståndet (friktion). Det är i princip luftmotståndet som bestämmer hastigheten. Vad händer då med en skidåkare som lägger på hullet? Jo han eller hon blir lite större och lite tyngre. Men eftersom volymen av en ideal klotformig skidåkare går som r³ medan ytan går som r², så ökar massan (volymen) snabbare än ytan med faktorn r. Kraften som drar skidåkaren nedåt är ju proportionell mot massan, medan kraften som bromsar (luftmotståndet) är proportionell mot ytan. Vi får allstå en större kraft för den tyngre skidåkaren, medan luftmotståndet inte ökar lika mycket. Så om allt annat är lika så har en tyngre åkare en fördel.

Vad gäller glidfriktion mellan snön och skidorna är den propotionell mot normalkraften som är proportionell mot massan. För denna har alltså skidåkarens vikt ingen betydelse eftersom både friktionen och den dragande kraften är proportionell mot massan.

Se även fråga 20012 .
/PE

Nyckelord: friktion [53]; bobåkning/störtlopp [4]; *idrottsfysik [42]; luftmotstånd [11];

1 http://www.nbclearn.com/portal/site/learn/resources

Svar:
Om vinden kommer rakt bakifrån går det inte. Om vinden kommer från sidan, har båtens hastighet inte så mycket med vindens hastighet att göra.

Vindens verkan på seglet resulterar i en kraft, som verkar på båten genom masten. Vilken hastighet båten får beror på båtskrovet. En klumpig båt går långsamt. En långsmal, smäcker båt går snabbt, och den hastigheten kan vara större än vindens.

Det finns en detaljerad förklaring under länk 1. Om vinden kommer snett framifrån tvingas den av seglet att vrida lite i riktning mot segelbåtens akter. Detta leder enligt regeln verkan och återverkan (Newtons tredje lag, se Newtons rörelselagar ), till en kraft med en komponent riktad mot fören. Det finns naturligtvis även en kraftkomponent i sidled, men segelbåtens köl hindrar båten att driva i sidled.
/KS

Nyckelord: segling [5]; *idrottsfysik [42];

1 http://www.phys.unsw.edu.au/~jw/sailing.html

Svar:
Det är ingen lätt fråga att ge ett kort och uttömmande svar på. Effekten kallas för magnuseffekten. I många böcker finns det missvisande "förklaringar" till fenomenet. Se länk 1 för en avancerad beskrivning av magnuseffekten och aerodynamisk lyftkraft för en flygplansvinge. I Magnus_effect finns en parametrisering av storleken på lyftkraften.

Låt oss i den följande diskussionen anta att vi har slagit en underskruvad boll. Tänk på bordtennis eller golf! Bollen får då en uppåtriktad kraft på grund av rotationen.

En viktig princip i strömningslära är att luften häftar vid bollen. Vid bollens yta finns alltså ett tunt luftlager som följer med bollen.

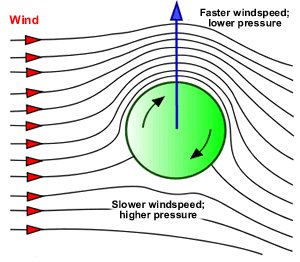
Det är rätt lätt att övertyga sig om att luften strömmar fortare ovanför än under bollen. (Vi betraktar luftens hastighet relativt bollen.) Luften som går snabbare över bollen måste accelereras. För detta krävs en tryckskillnad. Trycket är alltså lägre rakt över bollen än långt bort från bollen. Med samma argument visar man att trycket är högre strax under bollen. Tryckkrafterna påverkar alltså bollen uppåt! Se nedanstående figur.

Ett annat sätt att se problemet är att bollens rotation "drar isär" luften på ovansidan och "trycker ihop" luften på undersidan. Vi får alltså lågt tryck på ovansidan och högt tryck på undersidan. Denna tryckskillnad ger upphov till en lyftkraft.

Experiment: Be en kamrat slå en bordtennisboll hårt med mycket underskruv. Stå vid sidan och studera bollbanan. En golfboll beter sig likadant men är svårare att studera.

Nyckelord: golfboll [15]; skruvad boll [10]; *idrottsfysik [42]; flygplansvinge [8];

1 http://www.mathpages.com/HOME/kmath258/kmath258.htm

Ämnesområde	BlandatElektricitet-MagnetismEnergiKraft-RörelseLjud-Ljus-VågorMateriens innersta-Atomer-KärnorPartiklarUniversum-Solen-PlaneternaVärme
Sök efter
Grundskolan eller gymnasiet?	FörskolaGrundskolaGymnasiumLärarutbildning
Nyckelord:	#ljus [63]*astronomi/astrofysik och rymdfart [2]*biologi [20]*fysikaliska definitioner [1]*fysiologi [13]*geologi [16]*idrottsfysik [42]*kemi [22]*meteorologi [20]*miljöpåverkan [14]*nöjesparksfysik [12]*vardagsfysik [64]*verktyg [15]3d-bilder [6]aberration [1]absoluta nollpunkten [9]acceleration [6]accelerator [7]addition av hastigheter [2]aerosol [4]akustik [6]alfasönderfall [7]annihilation [14]antimateria [16]arbete [24]Arkimedes princip [32]asteroid [10]astrobiologi [9]astrologi [5]atomradie [8]Avogadros tal [3]ballong [25]bandgenerator [3]barometerformeln [1]batteri [25]belysning [6]bernoullieffekten [6]betasönderfall [15]big bang [37]bildskärmar [4]bindningsenergi [23]blixt [18]blå himmel [12]bobåkning/störtlopp [4]Bohrs atommodell [9]Bose-Einstein-kondensat [6]brandvarnare [2]bränslecell [3]centrifugalkraft [15]centripetalkraft [11]comptonspridning [3]corioliskraft [7]dagens längd [3]daggpunkten [2]dagjämning [6]Darwins evolutionsteori [8]de Broglie våglängd [1]decibel [11]delton [2]diffraktion [4]diffusion [1]dimensionsanalys [7]dimkammare [2]dopplereffekt (ljud) [3]dopplereffekt (ljus) [3]drickande fågeln [1]dubbelspalt [4]duschdraperi [2]Einstein, Albert [1]eko [3]elasticitet [4]elastisk stöt [12]elektrisk krets [7]elektrisk ström, hastighet [4]elektrisk ström, skada [6]elektromagnetisk strålning [21]elektronskal [12]elektrostatik [4]elsäkerhet [18]energikällor [26]energilagringssystem [7]enkelspalt [1]entropi [7]EPR, Bell, Aspect [3]evighetsmaskin [14]exoplaneter [17]fallrörelse [31]faradaybur [10]fasdiagram [7]felberäkning [6]Fermats princip [1]ferromagnetism [9]fiberoptik [4]fission [15]fluorescens [6]flygplansvinge [8]flykthastighet [4]formel 1 [2]forskningskarriär [1]fossila bränslen [13]fotoelektrisk effekt [7]foton [6]friktion [53]friktionskoefficient [5]frågelådan [14]Fukushima [6]fusion [17]fysik [10]fysik, förståelse av [17]fysik, historia [1]fysik, nytta med [6]fysikalisk modell [12]färg/färgseende [39]färgkraften [8]Gaia [3]galax [28]gamma ray burst [2]gaslagen, allmänna [24]generator [1]genomskinlighet [18]genteknik [2]geodesi/gravimetri [2]geostationär satellit [8]gitter [5]g-krafter [18]glasögon [2]gluoner [7]glödlampa [23]gnistkammare [1]golfboll [15]GPS [3]gravitation [7]gravitationslins [5]gravitationsvågor [19]gravity assist [2]gregorianska kalendern [1]grundämnen, bildandet av [5]grundämnen, förekomst [4]gränshastighet [4]gunga [4]gyroskop [1]halofenomen [2]halogenlampa [3]halveringstid/sönderfallskonstant [5]harmonisk svängning [4]Heisenbergs obestämdhetsrelation [12]helikopter [5]higgspartikeln [10]Hiroshima/Nagasaki [4]hologram [5]HR-diagram [3]Huygens princip [3]hyperfinstruktur [1]hägring [4]händelsehorisont [4]hävstång [5]hörsel [10]Illustrerad Vetenskap [17]impedans [3]induktans [6]induktion [13]inertialsystem [6]inflation [7]infraljud [7]interferens [14]Internationella rymdstationen [6]iskristaller [5]istider [8]joniserande strålning [4]jordens atmosfär [12]jordens inre [14]jordens magnetfält [22]jordens rotation [22]kall fusion [8]kaos [3]kapillärkraft [12]kastparabel [10]Keplers lagar [14]Kirchhoffs strålningslag [4]klimat [11]knäppande aluminiumfolie [2]kokande vatten [17]kokpunkts/fryspunkts förändring [14]kol [3]kol-14 metoden [4]koldioxidcykeln [6]kollisionssäkerhet [1]komet [14]kosmisk bakgrundsstrålning [19]kosmisk strålning [5]kosmologi [33]kraft [12]kraftledning [7]kraftverkningar [9]kursplan [3]kvantmekanik [30]kvark [12]kvasar [4]kylning [7]kärndata [3]kärnenergi [19]kärnfysik [2]kärnkrafter [7]kärnkraftsavfall [11]kärnreaktion [5]kärnvapen [16]Lagrange-punkt [2]latitud/longitud [1]lins [11]liv i universum [9]livets uppkomst [1]ljud [11]ljud, interferens [7]ljud, resonans [19]ljudbang [3]ljudhastigheten [21]ljusbrytning [26]ljushastigheten [24]ljusreflektion [18]lorentztransformation [2]luftmotstånd [11]lufttryck [23]luminiscens [5]lutande plan [15]lysdiod [14]lysrör [10]lågenergilampa [13]längdkontraktion [6]magnetisk monopol [4]magnetism [52]magnetron [1]Mars [12]massa, trög/tung [4]massa-energi [1]massa-kraft [1]massbestämning [2]mass-luminositetsrelation [2]matematik i fysik [6]matematik, skriva [2]materia [6]Maxwells ekvationer [3]metabolism [3]metall, smältpunkt [3]meteorit [21]mikrovågsugn [25]Milankovitch cykler [3]mobiltelefon, strålning från [6]monstervåg [4]Monte Carlo-metoder [1]Mpemba-effekten [2]MRI [5]musikinstrument [19]månens bana [14]månens synbara storlek [1]månfärder [7]mörk energi [6]mörk materia [17]nanoteknik [6]Nationalencyklopedin [1]naturkonstant [7]naturlig radioaktivitet [3]nebulosa [13]NEO [10]neutrino [19]neutron [4]neutronstjärna [11]Newtons gravitationslag [12]Newtons rörelselagar [21]Newtons vagga [2]norrsken [7]nova [1]nyheter [11]Olbers paradox [2]orgelpipa [4]osmos [8]parallaxmetoden [4]parapsykologi [6]parbildning [7]Pascals lag [5]pauliprincipen [10]pendel, konisk [2]pendel, plan [9]PET [1]Plancks strålningslag [6]planet [17]planeters atmosfär [4]planeters form [3]plastfolie [1]polarisation [7]polaroidglasögon [3]potential/potentiell energi [30]prisma [1]projektarbete [1]pseudovetenskap [11]QED [7]radioaktiv datering [7]radioaktivitet, sönderfallskedja [7]radioaktivt sönderfall [38]radioteleskop [1]radon [4]raketekvationen [2]raketmotor [8]regn [1]regnbåge [6]relativistiskt massberoende [4]relativitetsteorin, allmänna [33]relativitetsteorin, speciella [45]religion [3]resistans [15]resistansförluster [2]resonans [5]richterskalan [2]ringklocka [5]rymddräkt [5]rymdfärder [23]rödförskjutning [7]röntgenrör [3]rörelseenergi [14]rörelsemängd [15]rörelsemängdsmoment [14]satellitbana [15]Saturnus´ ringar [6]schrödingerekvationen [4]Schrödingers katt [2]science fiction [6]segling [5]serie- och parallellkoppling [19]SETI [1]shareware [1]SI-enheter [6]skruvad boll [10]skymning [1]slumptal [1]SN 1987A [4]solaktivitet [2]solarkonstanten [6]solcell [7]solen [5]solen, avstånd till [1]solenergi [14]solens energiproduktion [9]solens utveckling [4]solförmörkelse [3]solsystemet [8]solsystemet, avstånd och rörelse [3]solsystemets bildande [12]specifik värmekapacitet [25]spegel [10]spektrum [11]standardmodellen [24]statisk elektricitet [12]stearinljuslåga [16]stjärna [4]stjärnhimlen [12]stjärnors utveckling [15]stroboskopeffekt [3]strålning, faror med [26]strålning, in-/ut- [6]strängteori [7]strömning [1]supernova [13]supertunga grundämnen [1]supraledning [7]svart hål [51]synvilla [6]sönderfallskonstant [5]teleskop [10]temperatur/temperaturskalor [17]temperaturstrålning [29]termodynamik [17]termometer [8]termos [3]Three Mile Island [3]tid [10]tidsdilatation [6]tidsekvation [4]tidvatten [15]tjerenkovstrålning [2]Tjernobyl [12]totalreflektion [9]transformator [6]transmutation av kärnavfall [2]trefas [3]trippelpunkt [2]tröghetsmoment [9]tsunami [5]tunneleffekt [3]TV [9]tvillingparadoxen [5]tyngdaccelerationen [16]tyngdlöshet [13]ultraljud [9]universums expansion [16]uppvärmning av bostäder [2]utvidgning [8]UV-ljus [13]vakuum [9]vatten/is [49]vattenkraft [7]vattenpump [2]vattenånga [2]Venus [11]verkningsgrad [26]vetenskaplig metod [18]Wikipedia [5]WIMPs [3]vindavkylning [4]vindenergi [12]Vintergatan [6]vridmoment [7]vulkanism [5]våg/partikelegenskaper [8]vågenergi [3]vågfunktion [2]värmemängd [3]värmepump/kylskåp [8]värmeöverföring/transport [46]väteatomen [2]vätskedroppsmodellen [5]växthuseffekten [36]ytspänning [18]årstider [4]ögat [18] (Enda villkor)
Definition:	(transmissions)mediumabsoluta nollpunktenabsorptionsspektraaccelerationackommodationackretionsskivaadiabatisk processaerodynamic heatingaerosolaggregationstillståndakustisk impedansallmänna gaslagenampereamperetimmeannihilationantigravitationantimateriaantropiska principenarbetearkimedes principasteroidasteroidbältetastigmatismastrobiologiastronomisk enhetatommassaatomnummeravogadros talbandspektrabatteribenhams snurrabergvärmebernoullis ekvationbetasönderfallbig bangbindningsenergibindningsenergibioluminiscensboltzmanns konstantbose–einstein-kondensatbrewstervinkelnbrownsk rörelsebrytningsindexbrännpunktbubbelkammarecarnotprocesscentrifugalkraftcentripetalkraftcirkumpolära stjärnorcitronbattericorioliskraftencurietemperaturendarwins evolutionsteoride broglie våglängdendecibeldeltonden kosmologiska principendensitetdielektrisk polarisationdielektriskt materialdiffus reflektiondiffusiondigitalkameradimensiondioptridiskret spektrumdispersiondopplereffektdotternukliddulong-petits lage=mc2ekliptikanekoekvivalensprincipenelasticitetelastisk energieldelektrisk dipolelektrisk laddningelektrisk spänningelektrisk strömelektriska fältstyrkanelektroluminiscenselektromagnetisk strålningelektroninfångningelektronskalelementarladdningenelementarpartiklaremissionsnebulosaemissionsspektraemsendoterm reaktionenergienergikällaenergiomvandlingenergipincipenenergipotentialentropi (makroskopisk definition)entropi (mikroskopisk definition)evighetsmaskinexciterade tillståndexoplanetexoterm reaktionextremofilerfallrörelsefaradays burfasdiagramfermats principferminivånferromagnetismfissionfjärde generationens reaktorfluidfluorescensflygplansvingeflykthastighetenfokalpunktfokusfosforescensfossila bränslenfotokromismfotomotståndfotonfotosfärenfotosyntesfouriers lagfraktalfranck-hertz försökfriktionfriktionskoefficientfritt fallfukushimafundamentala naturkrafternafusionfysikfysikaliska modellerfysiologifärgfärgblindhetfärgseendefönybara bränslenförnybara energikällorgaiagalaxgammastrålninggaskonstantengeneratorgeostationär satellitgeotermisk energiglobal uppvärmninggluonerglödlampagravitationgravitationengravitationskonstantengravitationsvågorgrundläggande fysikgrundtillståndetgrundtongrundämnegrå starrgränshastighetgula fläckenhalleffekthalogenlampahalveringstidhastighethawkingstrålningheisenbergs obestämdhetsrelationhertzsprung-russell diagramhiggspartikelnhookes laghornhinnanhubble ultra deep fieldhuygens principhydrostatiska paradoxenhägringhändelsehorisontenhästkrafthävstångicke-joniserande strålningideal gasimpedansinduktansinduktioninertialsysteminflationinfraljudinfraröd strålninginklinationinre konversioninre resistansinterferensinverterad populationisomerisospinnisoterm processisotoperjondriftjoniserande strålningjordfelsbrytarekalibreringkall fusionkalorikapacitanskapillärkraftenkastparabelkedjereaktionkemisk bindningkemisk bindningkemisk reaktionkemoluminiscenskeplers andra lagkeplers första lagkeplers tredje lagkilogramkirchhoffs lagkirchhoffs strålningslagkiselklassisk fysikklorofyllkokarreaktorkokpunktkolkornsmikrofonkometkomplementfärgkondensatorkonduktanskonservativ kraftkonserveringslagkontinuerligt spektrumkonvektionkoronankorrespondesprincipenkosmiska bakgrundsstrålningenkosmologikosmologiska rödskiftetkosmologiska standarmodellenkraftkristallkritisk densitetkritisk massakromosfärenkuiperbältetkundts rörkvantdatorkvantmekanikkvantmekanisk sammanflätningkvarkkvark-gluon plasmakvartskvasarkvasipartiklarkärnkrafterkärnreaktionkärnreaktorerkärnvapenlagrange-punkternalaserlenz lagleptonlila linjespektralivljudljusljusabsorptionljusbrytningljushastighetenljuskällorljusutbyteljusårlongitudinell våglorentzkraftenluftmotståndluminiscenslutande planlysdiodlysrörlågenergilampalägesenergilängdkontraktionmachomagnetismmagnuseffektenmarkradarmarkvärmemaskhålmassamasscentrummassdefektmassenhetmassexcessmasstalmateriamaxwell–boltzmannfördelningenmaxwells ekvationermedelvärdetmegaton tntmeissnereffektenmekanikens gyllene regelmerkurius periheliumprecessionmetafysikmetallbindningmetalldetektormetallicitetmeteormeteoritmeteoroidmilankovitch cyklermodern fysikmodernuklidmolmolekylmultiversummymetallmånemätfelmörk energimörk materiamörk nebulosamössbauer-effektennanometertekniknanopartikelnanotekniknationalencyklopedinnaturvetenskapnavigeringneoneutrinoneutrinooscillationerneutroninducerad fissionneutronstjärnanewtonnewtonringarnewtons andra lagnewtons avsvalningslagnewtons första lag (tröghetslagen)newtons gravitationslagnewtons tredje lagnobelpris i fysik 1925nobelpris i fysik 1993nobelpris i fysik 2015nobelpris i fysik 2017nobelpris i fysik 2020normalkraftennorrskennuklidnuklidkartanutida fysiknärsynthetockhams rakknivohms lagoorts kometmolnoregelbunden galaxosmosparapsykologiparbildningpascals princippauliprincipenperiodiska systemetplanck timeplancks strålningslagplanetplanetarisk nebulosaplasmaplasmaplasmaplasticitetpn-övergångpolarisationpolspänningpolär jetstrålepotentialproton-protonkedjanpseudovetenskapqcdqedradiative forcingradioaktivitetradioluminiscensraketekvationenrayleigh-spridningreaktansreflektionreflektionsnebulosarefraktionregnbågerelativ luftfuktighetrelativistisk energirelativistisk jetresistansresistivitetresistivitetresonansroche-gränsenrullmotståndrussells tekannarödförskjutningrörelseenergirörelsemängdrörelsemängdsmomentschwarzschildradiensekulär jämviktsekundsfärisk aberrationsi-enheternasingularitetsi-prefixsi-systemetsjälvinduktansskalärproduktskottsekundslipstreamslumpvisa mätfelsmältvärmesnells lagsolarkonstantensolcellersolenergisolens centrumsolförmörkelsesolkraftverksolvindsolvärmespallationspecifik värmekapacitetspektroskopispektrumspinnspontan fissionstandardavvikelsenstandardmodellenstatisk elektricitetstefan–boltzmanns lagstimulerad emissionstjärnastjärnbildstorhetstrålningstrålningstråloptiksträngteorinstående vågstämgaffelsublimationsupermassiva svarta hålsupernovasupertungt grundämnesuprafluiditetsupraledningsvart hålsvartkroppsvänghjulsystematiska mätfelsåpbubblasäkringsönderfallskedjasönderfallskonstantentemperaturtemperaturspektrumtemperaturstrålningtensortermodynamiktermodynamikens andra huvudsatstermodynamikens första huvudsatsthree mile islandtidtidens riktningtidsdilatationtidsekvationentidvattentidvattenkraftertillämpad fysiktjerenkovstrålningtjernobyltotalreflektiontransformatortransistortransparenstriboelektrisk effekttrippelpunktentrycktryckvattenreaktortröga massantröghettröghetsmomenttunga massantvillingparadoxentyngdtyngdaccelerationtyngdlöshettyngdpunktentyp ii supernovaufoultraljudultraviolett strålningultraviolettkatastrofenunderkylninguniversums åldervakuumvakuumfluktuationervakuumpolarisationvalenselektronvattenburen värmevattenkraftvattenkraftvattenångavektorerverkningsgradvetenskaplig metodwiens förskjutningslagwikipediaviktwimpvindkraftvintergatanvintergatanvirtuell bildvirtuell bildvit dvärgvoltvridmomentv-t diagramvåglängdenvåg-partikeldualitetvågtalvärmeledningvärmemängdvärmepumpvärmepumpvärmeöverföringvätebindningvätelika jonervätskedroppsmodellenväxthuseffektenytenergiångbildningsvärmeångtryckårstidernaåskaädelgasädelgaserögats linsöratöversynthetövertoner (Enda villkor)

---

Om du inte hittar svaret i databasen eller i

Sök i svenska Wikipedia:

Sök i Nationalencyklopedin

   

Sök med Google

   

- fråga gärna här.