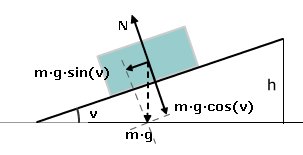
Om en kloss åker nedför ett lutande plan med konstant hastighet kan man då räkna ut friktionskraften genom att ta mgh/sträckan? Då varken vinkel, hastighet eller friktionskoefficent är angiven? Vi ska dessutom inte räkna med cos o.s.v. just nu. Så letar efter ett annat räknesätt.

Tack för svar
/Madeleine J

Svar:
Nej det går inte. Du har alldeles för lite uppgifter: bara att hastigheten är konstant. Se exempel 2 i länk 1.
/Peter E

Nyckelord: lutande plan [15];

1 http://fysikhjalp.se/kraftmoment/kraftvektorer/kraftvektorer_sida.html

Sedan undrar jag också om man har en donut istället för en låda på ett lutande plan. Hur ska då normalkraften och tyngdkraften ritas ut?
/Samuel M, Larskaggskolan, Kalmar

Svar:
Normalkraften är den vinkelräta komposanten av den kontaktkraft som hindrar ett objekt att tränga igenom en yta. På mikroskopisk skala har normalkraften sitt ursprung i de elektromagnetiska krafter som verkar mellan atomerna i kropparnas ytor.

Vektorn normalkraften (bilden nedan) är alltså en representation av alla krafter som hindrar lådan att tränga igenom underlaget. Om man förutsätter att lådan inte kan rotera, så kan man låta normalkraften angripa var som helst. Tyngdkraften skall naturligtvis angripa i tyngdpunkten, så det är praktiskt att placera normalkraften där också.

Se vidare länk 1, Normal_force och fråga 13477 .

Nyckelord: lutande plan [15];

1 http://hyperphysics.phy-astr.gsu.edu/hbase/frict.html#nor

Svar:
Arbetet är lika stort bara om du kan bortse från friktion. Om du har friktion får du förluster som blir till värmeenergi. Arbetet går alltså till att lyfta föremålet och att motverka friktionen. Se fråga 20415 för ett genomräknat exempel.
/Peter E

Nyckelord: lutande plan [15]; friktion [53];

Ursprunglig fråga:
Om man drar en låda med konstant hastighet uppför ett lutande plan och ska undersöka verkningsgraden för olika vinklar. Arbetet ses som den tillförda energin och lägesenergin ses som den nyttiga energin.

Våra resultat visar att större vinklar ger större verkningsgrad. Är detta sant? Varför/varför inte?
/Denizé Z, TBS, Örebro

Svar:
För att dra lådan uppför planet krävs en kraft som är lika med summan av friktionskraften µ·N=µ·m·g·cos(v) och tyngdkraftens komposant m·g·sin(v), alltså dragkraften, se länk 1 och nedanstående figur från länk 1:

F = µ·m·g·cos(v) + m·g·sin(v)

Potentiell energi på höjden h: mgh

Arbete: (µ·m·g·cos(v) + m·g·sin(v))·h/sin(v)

Verkningsgrad = e = Potentiell energi/Arbete

e = sin(v)/((µ·cos(v) + sin(v)) = 1/(µ·cot(v) + 1)

Låt oss se om detta är rimligt. Utan friktion (µ=0) ger e=1 som sig bör.

Om vinkeln v=0^o blir e=0. Om v=90^o blir e=1. Dessa extremfall motsvarar mycket friktion (lång sträcka, hög normalkraft) och ingen friktion (lådan dras vertikalt utan att röra planet).

Om v=45^o och µ=0.2 blir e=1/(0.2+1)=0.83.

Som du ser är det korrekt att stor vinkel ger högre verkningsgrad.

Nyckelord: friktion [53]; lutande plan [15];

1 http://www.kursnavet.se/kurser/fy1201/fy1201w/M1_1_0_070-friktion-lutande.htm

Ursprunglig fråga:
Vad är det som spelar roll för vilken av innebandybollen eller bocciabollen som kommer snabbast ner för en rutschkana?
/Isak K, Europaportens skolor, Malmö

Svar:
För ett icke rullande föremål på ett lutande plan omvandlas potentiell energi till rörelseenergi. Om vi kan borse från friktion kommer alla föremål att ha samma hastighet nedför planet:

mgh = mv²/2

v = sqrt(2gh)

Den viktigaste skillnaden om föremålet rullar är relativt tröghetsmoment. (Vi förutsätter att bollarna rullar utan friktionsförluster och glid.) Tröghetsmomentet beror av massfördelningen. Mycket massa nära ytan av bollen och stor radie ger högt tröghetsmoment och därmed mer rotationsenergi för en given rotationshastighet. Denna tas från den vanliga rörelseenergin, vilket saktar ner den linjära rörelsen.

Rullande föremål med högt tröghetsmoment rullar alltså långsammare än föremål med lågt tröghetsmoment. Bocciabollen är homogen av metall (Bocce ). En innebandyboll är ihålig och av plast (Innebandyboll ). Massfördelningen skulle ge ett högt tröghetsmoment för innebandybollen och lägre för bocciabollen. Densiteten är emellertid mycket högre för bocciabollen, så jag tror denna rullar saktare. Det hade varit enklare om bollarna varit av samma material och med samma radie.

Se fråga 20352 och 14738 för mer om rullande kulor.

I länk 1 och 2 finns tröghetsmomentet för några olika objekt. Om massan och radien är lika får vi följande för sluthastigheten:

kloss (ingen rotation): sqrt(2gh) = 1.41*sqrt(gh)
boll: sqrt((10/7)*gh) = 1.20*sqrt(gh)
cylinder: sqrt((4/3)*gh) = 1.15*sqrt(gh)
ring: sqrt(1*gh) = 1*sqrt(gh)
/Peter E

Nyckelord: lutande plan [15]; tröghetsmoment [9];

1 http://hyperphysics.phy-astr.gsu.edu/hbase/sphinc.html
2 http://hyperphysics.phy-astr.gsu.edu/hbase/hoocyl.html#hc1

Svar:
Lina! Det grundläggande med ett lutande plan är att lägesenergi omvandlas till rörelseenergi. En komplikation är att man ofta behöver ta hänsyn till friktionsförluster. För ett glidande föremål använder du den vanliga friktionskoefficienten. I detta fallet är det ojämnheter i föremålet och i underlaget som ger en bromsande kraft.

För ett hjul eller en kula har man vad som kallas rullmotstånd, se Rullmotstånd . Detta uppstår genom att normalkraften deformerar kulan/hjulet och/eller underlaget. Matematiskt behandlas rullmotstånd som friktion och friktionskraften ges av det vanliga uttrycket F=mN.

För att en kula eller ett hjul skall rulla på en yta behövs friktion. Man antar normalt att friktionen är tillräcklig så att kulan/hjulet inte glider alls.

Det tillkommer emellertid lite komplikationer för rullande föremål. För det första kommer en del av rörelseenergin som skapas av det lutande planet att bli till rotationsenergi. I fråga 14738 visas att rotationsenergi och rörelseenergi för en homogen kula förhåller sig som 2:5.

Dessutom kan föremålet både glida och rulla (bromsande bil). Då blir det riktigt besvärligt och risk att eleverna flyr.
/Peter E

Nyckelord: friktion [53]; lutande plan [15];

A: Vilken fart har tegelpannan när den rutschar av taket?

B: Använd svaret från "A" för att beräkna hur lång långt ut från husväggen som tegelpannan träffar marken. Det är 4 m från takkanten till marken.

Nu del A tror jag att jag har klarat fick 4,5m/s genom att likställa rörelseenergi med läges där h=s*sin(v). men det finns inget facit är otroligt tacksam för hjälp och vägledning. Glad påsk!
/edin R

Svar:
Uppgiften kommer från länk 1. Eftersom problemet innehåller friktion kan du inte använda energikonservering utan friktionsförluster (se emellertid nedan). ________________________________________________________________

A Vi börjar med att beräkna den resulterande kraften F_r från skillnaden mellan tyngdkraftens komponent nedåt parallellt med planet och friktionskraften, se figur nedan:

F_r = mg(sinq - m*cosq) = mg(sin(25) - 0.2*cos(25)) = mg*0.2414 N

Accelerationen a ges av

a = F/m = g*0.2414 = 9.81*0.2414 = 2.368 m/s²

Vi räknar ut tiden t på planet från

s = at²/2

t = sqrt(2*s/a) = sqrt(2*5/2.368) = 2.055 s

Sluthastigheten vid takets slut blir då

v = a*t = 2.368*2.055 = 4.866 m/s

Låt oss kolla detta svar genom att tillämpa energins bevarande

Potentiella energin i startläget är

mgh = m*9.81*sinq *5 = m*9.81*sin(25)*5 = 20.73m J

Rörelseenergin på takkanten blir

E_k = m*v²/2 = m*4.866²/2 = 11.84m J

Friktionsförlusterna är

E_f = kraften*vägen = mg*m*cosq*5 = m*9.81*0.2*cos(25)*5 = 8.89m J

Summan av E_f och E_k blir

8.89m + 11.84m = 20.73m J

vilket stämmer bra med potentiella energin ovan. ________________________________________________________________

B Vi delar vi upp hastigheten vid takkanten i en horisontell och en vertikal komponent:

v_h0 = v₀*cos(25) = 4.866*cos(25) = 4.410 m/s

v_v0 = v₀*sin(25) = 4.866*sin(25) = 2.056 m/s

För rörelsen i vertikalled (fritt fall) gäller (ekv. 4 i fråga 18438 )

v_v² = v_v0² + 2as = 2.056² + 2*9.81*4 = 82.71 (m/s)²

dvs

v_v = 9.095 m/s

Vi räknar ut falltiden t från

s = v_v0*t + gt²/2 = 2.056*t + 9.81*t²/2

dvs

9.81t² + 2*2.056*t - 2*4 = 9.81t² + 4.112t - 8 = 0

med lösningen

t = 0.7175 s (det finns även en ogiltig negativ lösning)

Rörelsen i horisontalled sker med konstant hastighet. När takpannan når marken efter 0.7175 s har den färdats sträckan

s = v_ht = 4.410*0.7175 = 3.16 m

Vi kollar resultatet med energiprincipen. Totala energin i förhållande till marken (före start):

mgh = m*9.81*(sin(25)*5+4) = 59.97m J

Totala hastigheten vid marken blir

V = sqrt(v_h² + v_v²) = sqrt(4.410² + 9.095²) = 10.108 m/s

E_kin + E_f = m(10.108²/2 + 8.89) = 59.98m J

vilket stämmer bra med ovanstående värde för den totala potentella energin.

Nyckelord: friktion [53]; lutande plan [15]; fallrörelse [31]; acceleration [6];

1 https://www.hb.se/PageFiles/204024/Naturvetenskap_160114.pdf
2 http://hyperphysics.phy-astr.gsu.edu/hbase/frict2.html#plo

Svar:
Om du menar hur stor rörelseenergi blocket får om man kan bortse från friktionen så blir kinetiska energin mgh. Den beror alltså bara av den vertikala höjden.

Om friktionen inte är försumbar kommer blocket ner med lägre energi - resten blir till värme. Om friktionen är stor och vinkeln liten fastnar blocket.
/Peter E

Nyckelord: lutande plan [15]; friktion [53];

Svar:
Hej Malin! För att uppskatta friktionsförluster kan man beräkna den totala energin i en punkt på höjden h. Med traditionella beteckningar är (potentiell energi + rörelseenergi)

mgh + mv² = mgH (1)

där H är starthöjden.

För att kulan inte skall ramla ner i toppen av loopen måste centripetalaccelerationen minst vara lika med g, dvs

v²/r = r

dvs

mv²/2 = mgr/2

Den potentiella energin i toppen av loopen är mg*2r

Totala energin blir då

mg*2r + mgr/2 = mg(2.5r) (2)

där

2.5r = 27.5 cm --> r = 11 cm.

Startpunkten borde alltså ligga på höjden H = 2.5r. Detta är ju precis vad du räknat ut. Så varför stämmer det så dåligt med det experimentella värdet? Det kan vara både rullfriktion och luftmotstånd. Procenten friktionsenergiförluster med dina värden blir

(37-27.5)/37 = 26%

vilket verkar mycket. Detta är allt du kan räkna ut utan att göra hastighetsmätningar längs hela banan, eftersom (som du säger) friktionskoefficienten varierar längs banan.

Du har emellertid försummat kulans rotationsenergi. Av fråga 14738 framgår att rotationsenergin är 2/7 och translationsenergin 5/7. Vi måste alltså korrigera uttrycket (2) för rotationsenergin:

mg*2r + (mgr/2)*(7/5) = mg(2.7r) (3)

Detta ger det teoretiska värdet på starthöjden till

H = 2.7*11 = 29.7

och friktionsandelen

(37-29.7)/37 = 20%
/Peter E

Nyckelord: lutande plan [15]; potential/potentiell energi [30]; friktion [53];

Svar:
Ja, accelerationen är konstant om man kan bortse från friktion och luftmotstånd.

Om man ökar planets vinkel blir även komponenten av tyngdkraften längs med planet (mg*sin(theta) i figuren nedan) större. F=ma ger då att accelerationen är proportionell mot kraften. Observera att komponenten av tyngdkraften vinkerätt mot planet (mg*cos(theta)) tas ut av normalkraften N så den har ingen inverkan på vagnens rörelse.

Se vidare Inclined_plane .

Nyckelord: lutande plan [15];

Ursprunglig fråga:
Hejsan! Jag har ett problem. En kula släpps i en kulbana som står placerad på ett bord, vid kanten. Jag har räknat fram att kulan har fått en viss teoretisk energi när den lämnar banan och den har fått en minde energi i verkligheten.

Jag kan anse att luftmotståndet och friktionen inte har någon påverkan och jag har listat ut att det har något med rotationen av kulan att göra, så min fråga är nu. Vart tar energin vägen på sin resa ned för kulbanan?

svara gärna snabbt, arbetet ska lämnas in denna veckan..
/Anna O, Birger Sjöbergymnasiet, Vänersborg

Svar:
Ditt problem är inte helt lätt, du får nöja dig med en skiss. Lösningen finns under länk 1, men där på engelska.

Vi börjar med att bortse från kulans rotation. Antag kulans massa är m och dess sluthastighet v. Då gäller enligt energiprincipen (potentiell energi på höjden h = kinetisk energi vid botten):

mgh = mv²/2

dvs

v² = 2gh

Om kulan inte glider alls kommer den att sättas i rotation. Om tyngdpunktens hastighet i detta fallet är u, kommer vinkelhastigheten w att vara u/r där r är kulans radie. (Du får detta resultat eftersom den del av kulan som rör vid kulbanan har hastigheten 0 i förhållande till banan - kom ihåg, inget glid!).

En homogen kulas tröghetsmoment ges av J = 2mr²/5 (Tröghetsmoment#Exempel ) och rotationsenergin är Jw²/2.

Vi adderar translations-kinetiska energin och rotationsenergin och får

mgh = mu²/2 + (2mr²/5)(u/r)²/2 = mu²(1/2) + mu²(1/5)

dvs

u² = (10/7)gh = 1.43gh

Detta är klart mindre än 2gh som vi fick ovan eftersom ju en del energi går till kulans rotationsenergi. Förhållandet u/v blir ungefär 0.85, alltså 15% lägre hastighet än en kula som glider perfekt och inte roterar.

Förhållandet mellan rotationsenergi och translationsenergi blir enligt ovan

(1/5)/(1/2) = 2:5.

Tillägg om puttning i golf

Golfspelare som puttar bra ser till att slå till bollen med en något uppåtgående rörelse för att bollen om möjligt skall börja rulla omedelbart. Om man slår till bollen helt centralt kommer bollen att glida ett tag på gräset. Friktionen kommer efter ett tag att få bollen att rulla, men rotationsenergin måste tas från rörelseenergin. Bollen bromsas alltså upp för att den skall kunna få rotation. Det visar sig att längden på puttarna blir mycket mer konsistent om man kan få bollen att rulla direkt vid tillslaget.

Tekniken att få överspinn på bollen direkt vid tillslaget används även t.ex. i biljard då man oftast slår till bollen ovanför ekvatorsplanet vilket får bollen att börja rulla omedelbart.

/*fa*
/Peter E

Nyckelord: tröghetsmoment [9]; lutande plan [15]; *idrottsfysik [42]; rörelseenergi [14]; golfboll [15];

1 http://modeling.asu.edu/listserv/U7_KE_rolling_ball02.pdf

Svar:
Äntligen en riktig fysikfråga - det lutande planet är verkligen klassisk fysik !

Tyngdkraftens komponent längs det lutande planet är m*g*sin(v), där v är planets lutningsvinkel mot horisontalplanet. Accelerationen är alltså g*sin(v) om du kan bortse från friktion och kulans rotationsenergi. Om du alltså bestämmer accelerationen (t.ex. genom att bestämma hastigheten som funktion av tiden) kan du räkna ut g. Se fråga 14383 där man tar hänsyn till kulans rotationsenergi.
/Peter E

Se även fråga 14383

Nyckelord: lutande plan [15];

1 http://www.glenbrook.k12.il.us/gbssci/phys/Class/vectors/u3l3e.html
2 http://lectureonline.cl.msu.edu/~mmp/applist/si/plane.htm

Svar:
I fallet kastparabel, så faller kroppen helt fritt i vertikal-led - rörelsen i horisontal-led har ingen betydelse. För det lutande planet hindras det fria fallet av planet, och accelerationen blir mindre (med faktorn sinv) och vägen längre (också med faktorn sinv), ju mindre planet lutar. Därför blir tiden t₂ längre med faktorn 1/sinv (t₂²=2h/sin²v), som du mycket riktigt själv kommit fram till.
/Peter Ekström

Nyckelord: kastparabel [10]; lutande plan [15];

Ämnesområde	BlandatElektricitet-MagnetismEnergiKraft-RörelseLjud-Ljus-VågorMateriens innersta-Atomer-KärnorPartiklarUniversum-Solen-PlaneternaVärme
Sök efter
Grundskolan eller gymnasiet?	FörskolaGrundskolaGymnasiumLärarutbildning
Nyckelord:	#ljus [63]*astronomi/astrofysik och rymdfart [2]*biologi [20]*fysikaliska definitioner [1]*fysiologi [13]*geologi [16]*idrottsfysik [42]*kemi [22]*meteorologi [20]*miljöpåverkan [14]*nöjesparksfysik [12]*vardagsfysik [64]*verktyg [15]3d-bilder [6]aberration [1]absoluta nollpunkten [9]acceleration [6]accelerator [7]addition av hastigheter [2]aerosol [4]akustik [6]alfasönderfall [7]annihilation [14]antimateria [16]arbete [24]Arkimedes princip [32]asteroid [10]astrobiologi [9]astrologi [5]atomradie [8]Avogadros tal [3]ballong [25]bandgenerator [3]barometerformeln [1]batteri [25]belysning [6]bernoullieffekten [6]betasönderfall [15]big bang [37]bildskärmar [4]bindningsenergi [23]blixt [18]blå himmel [12]bobåkning/störtlopp [4]Bohrs atommodell [9]Bose-Einstein-kondensat [6]brandvarnare [2]bränslecell [3]centrifugalkraft [15]centripetalkraft [11]comptonspridning [3]corioliskraft [7]dagens längd [3]daggpunkten [2]dagjämning [6]Darwins evolutionsteori [8]de Broglie våglängd [1]decibel [11]delton [2]diffraktion [4]diffusion [1]dimensionsanalys [7]dimkammare [2]dopplereffekt (ljud) [3]dopplereffekt (ljus) [3]drickande fågeln [1]dubbelspalt [4]duschdraperi [2]Einstein, Albert [1]eko [3]elasticitet [4]elastisk stöt [12]elektrisk krets [7]elektrisk ström, hastighet [4]elektrisk ström, skada [6]elektromagnetisk strålning [21]elektronskal [12]elektrostatik [4]elsäkerhet [18]energikällor [26]energilagringssystem [7]enkelspalt [1]entropi [7]EPR, Bell, Aspect [3]evighetsmaskin [14]exoplaneter [17]fallrörelse [31]faradaybur [10]fasdiagram [7]felberäkning [6]Fermats princip [1]ferromagnetism [9]fiberoptik [4]fission [15]fluorescens [6]flygplansvinge [8]flykthastighet [4]formel 1 [2]forskningskarriär [1]fossila bränslen [13]fotoelektrisk effekt [7]foton [6]friktion [53]friktionskoefficient [5]frågelådan [14]Fukushima [6]fusion [17]fysik [10]fysik, förståelse av [17]fysik, historia [1]fysik, nytta med [6]fysikalisk modell [12]färg/färgseende [39]färgkraften [8]Gaia [3]galax [28]gamma ray burst [2]gaslagen, allmänna [24]generator [1]genomskinlighet [18]genteknik [2]geodesi/gravimetri [2]geostationär satellit [8]gitter [5]g-krafter [18]glasögon [2]gluoner [7]glödlampa [23]gnistkammare [1]golfboll [15]GPS [3]gravitation [7]gravitationslins [5]gravitationsvågor [19]gravity assist [2]gregorianska kalendern [1]grundämnen, bildandet av [5]grundämnen, förekomst [4]gränshastighet [4]gunga [4]gyroskop [1]halofenomen [2]halogenlampa [3]halveringstid/sönderfallskonstant [5]harmonisk svängning [4]Heisenbergs obestämdhetsrelation [12]helikopter [5]higgspartikeln [10]Hiroshima/Nagasaki [4]hologram [5]HR-diagram [3]Huygens princip [3]hyperfinstruktur [1]hägring [4]händelsehorisont [4]hävstång [5]hörsel [10]Illustrerad Vetenskap [17]impedans [3]induktans [6]induktion [13]inertialsystem [6]inflation [7]infraljud [7]interferens [14]Internationella rymdstationen [6]iskristaller [5]istider [8]joniserande strålning [4]jordens atmosfär [12]jordens inre [14]jordens magnetfält [22]jordens rotation [22]kall fusion [8]kaos [3]kapillärkraft [12]kastparabel [10]Keplers lagar [14]Kirchhoffs strålningslag [4]klimat [11]knäppande aluminiumfolie [2]kokande vatten [17]kokpunkts/fryspunkts förändring [14]kol [3]kol-14 metoden [4]koldioxidcykeln [6]kollisionssäkerhet [1]komet [14]kosmisk bakgrundsstrålning [19]kosmisk strålning [5]kosmologi [33]kraft [12]kraftledning [7]kraftverkningar [9]kursplan [3]kvantmekanik [30]kvark [12]kvasar [4]kylning [7]kärndata [3]kärnenergi [19]kärnfysik [2]kärnkrafter [7]kärnkraftsavfall [11]kärnreaktion [5]kärnvapen [16]Lagrange-punkt [2]latitud/longitud [1]lins [11]liv i universum [9]livets uppkomst [1]ljud [11]ljud, interferens [7]ljud, resonans [19]ljudbang [3]ljudhastigheten [21]ljusbrytning [26]ljushastigheten [24]ljusreflektion [18]lorentztransformation [2]luftmotstånd [11]lufttryck [23]luminiscens [5]lutande plan [15]lysdiod [14]lysrör [10]lågenergilampa [13]längdkontraktion [6]magnetisk monopol [4]magnetism [52]magnetron [1]Mars [12]massa, trög/tung [4]massa-energi [1]massa-kraft [1]massbestämning [2]mass-luminositetsrelation [2]matematik i fysik [6]matematik, skriva [2]materia [6]Maxwells ekvationer [3]metabolism [3]metall, smältpunkt [3]meteorit [21]mikrovågsugn [25]Milankovitch cykler [3]mobiltelefon, strålning från [6]monstervåg [4]Monte Carlo-metoder [1]Mpemba-effekten [2]MRI [5]musikinstrument [19]månens bana [14]månens synbara storlek [1]månfärder [7]mörk energi [6]mörk materia [17]nanoteknik [6]Nationalencyklopedin [1]naturkonstant [7]naturlig radioaktivitet [3]nebulosa [13]NEO [10]neutrino [19]neutron [4]neutronstjärna [11]Newtons gravitationslag [12]Newtons rörelselagar [21]Newtons vagga [2]norrsken [7]nova [1]nyheter [11]Olbers paradox [2]orgelpipa [4]osmos [8]parallaxmetoden [4]parapsykologi [6]parbildning [7]Pascals lag [5]pauliprincipen [10]pendel, konisk [2]pendel, plan [9]PET [1]Plancks strålningslag [6]planet [17]planeters atmosfär [4]planeters form [3]plastfolie [1]polarisation [7]polaroidglasögon [3]potential/potentiell energi [30]prisma [1]projektarbete [1]pseudovetenskap [11]QED [7]radioaktiv datering [7]radioaktivitet, sönderfallskedja [7]radioaktivt sönderfall [38]radioteleskop [1]radon [4]raketekvationen [2]raketmotor [8]regn [1]regnbåge [6]relativistiskt massberoende [4]relativitetsteorin, allmänna [33]relativitetsteorin, speciella [45]religion [3]resistans [15]resistansförluster [2]resonans [5]richterskalan [2]ringklocka [5]rymddräkt [5]rymdfärder [23]rödförskjutning [7]röntgenrör [3]rörelseenergi [14]rörelsemängd [15]rörelsemängdsmoment [14]satellitbana [15]Saturnus´ ringar [6]schrödingerekvationen [4]Schrödingers katt [2]science fiction [6]segling [5]serie- och parallellkoppling [19]SETI [1]shareware [1]SI-enheter [6]skruvad boll [10]skymning [1]slumptal [1]SN 1987A [4]solaktivitet [2]solarkonstanten [6]solcell [7]solen [5]solen, avstånd till [1]solenergi [14]solens energiproduktion [9]solens utveckling [4]solförmörkelse [3]solsystemet [8]solsystemet, avstånd och rörelse [3]solsystemets bildande [12]specifik värmekapacitet [25]spegel [10]spektrum [11]standardmodellen [24]statisk elektricitet [12]stearinljuslåga [16]stjärna [4]stjärnhimlen [12]stjärnors utveckling [15]stroboskopeffekt [3]strålning, faror med [26]strålning, in-/ut- [6]strängteori [7]strömning [1]supernova [13]supertunga grundämnen [1]supraledning [7]svart hål [51]synvilla [6]sönderfallskonstant [5]teleskop [10]temperatur/temperaturskalor [17]temperaturstrålning [29]termodynamik [17]termometer [8]termos [3]Three Mile Island [3]tid [10]tidsdilatation [6]tidsekvation [4]tidvatten [15]tjerenkovstrålning [2]Tjernobyl [12]totalreflektion [9]transformator [6]transmutation av kärnavfall [2]trefas [3]trippelpunkt [2]tröghetsmoment [9]tsunami [5]tunneleffekt [3]TV [9]tvillingparadoxen [5]tyngdaccelerationen [16]tyngdlöshet [13]ultraljud [9]universums expansion [16]uppvärmning av bostäder [2]utvidgning [8]UV-ljus [13]vakuum [9]vatten/is [49]vattenkraft [7]vattenpump [2]vattenånga [2]Venus [11]verkningsgrad [26]vetenskaplig metod [18]Wikipedia [5]WIMPs [3]vindavkylning [4]vindenergi [12]Vintergatan [6]vridmoment [7]vulkanism [5]våg/partikelegenskaper [8]vågenergi [3]vågfunktion [2]värmemängd [3]värmepump/kylskåp [8]värmeöverföring/transport [46]väteatomen [2]vätskedroppsmodellen [5]växthuseffekten [36]ytspänning [18]årstider [4]ögat [18] (Enda villkor)
Definition:	(transmissions)mediumabsoluta nollpunktenabsorptionsspektraaccelerationackommodationackretionsskivaadiabatisk processaerodynamic heatingaerosolaggregationstillståndakustisk impedansallmänna gaslagenampereamperetimmeannihilationantigravitationantimateriaantropiska principenarbetearkimedes principasteroidasteroidbältetastigmatismastrobiologiastronomisk enhetatommassaatomnummeravogadros talbandspektrabatteribenhams snurrabergvärmebernoullis ekvationbetasönderfallbig bangbindningsenergibindningsenergibioluminiscensboltzmanns konstantbose–einstein-kondensatbrewstervinkelnbrownsk rörelsebrytningsindexbrännpunktbubbelkammarecarnotprocesscentrifugalkraftcentripetalkraftcirkumpolära stjärnorcitronbattericorioliskraftencurietemperaturendarwins evolutionsteoride broglie våglängdendecibeldeltonden kosmologiska principendensitetdielektrisk polarisationdielektriskt materialdiffus reflektiondiffusiondigitalkameradimensiondioptridiskret spektrumdispersiondopplereffektdotternukliddulong-petits lage=mc2ekliptikanekoekvivalensprincipenelasticitetelastisk energieldelektrisk dipolelektrisk laddningelektrisk spänningelektrisk strömelektriska fältstyrkanelektroluminiscenselektromagnetisk strålningelektroninfångningelektronskalelementarladdningenelementarpartiklaremissionsnebulosaemissionsspektraemsendoterm reaktionenergienergikällaenergiomvandlingenergipincipenenergipotentialentropi (makroskopisk definition)entropi (mikroskopisk definition)evighetsmaskinexciterade tillståndexoplanetexoterm reaktionextremofilerfallrörelsefaradays burfasdiagramfermats principferminivånferromagnetismfissionfjärde generationens reaktorfluidfluorescensflygplansvingeflykthastighetenfokalpunktfokusfosforescensfossila bränslenfotokromismfotomotståndfotonfotosfärenfotosyntesfouriers lagfraktalfranck-hertz försökfriktionfriktionskoefficientfritt fallfukushimafundamentala naturkrafternafusionfysikfysikaliska modellerfysiologifärgfärgblindhetfärgseendefönybara bränslenförnybara energikällorgaiagalaxgammastrålninggaskonstantengeneratorgeostationär satellitgeotermisk energiglobal uppvärmninggluonerglödlampagravitationgravitationengravitationskonstantengravitationsvågorgrundläggande fysikgrundtillståndetgrundtongrundämnegrå starrgränshastighetgula fläckenhalleffekthalogenlampahalveringstidhastighethawkingstrålningheisenbergs obestämdhetsrelationhertzsprung-russell diagramhiggspartikelnhookes laghornhinnanhubble ultra deep fieldhuygens principhydrostatiska paradoxenhägringhändelsehorisontenhästkrafthävstångicke-joniserande strålningideal gasimpedansinduktansinduktioninertialsysteminflationinfraljudinfraröd strålninginklinationinre konversioninre resistansinterferensinverterad populationisomerisospinnisoterm processisotoperjondriftjoniserande strålningjordfelsbrytarekalibreringkall fusionkalorikapacitanskapillärkraftenkastparabelkedjereaktionkemisk bindningkemisk bindningkemisk reaktionkemoluminiscenskeplers andra lagkeplers första lagkeplers tredje lagkilogramkirchhoffs lagkirchhoffs strålningslagkiselklassisk fysikklorofyllkokarreaktorkokpunktkolkornsmikrofonkometkomplementfärgkondensatorkonduktanskonservativ kraftkonserveringslagkontinuerligt spektrumkonvektionkoronankorrespondesprincipenkosmiska bakgrundsstrålningenkosmologikosmologiska rödskiftetkosmologiska standarmodellenkraftkristallkritisk densitetkritisk massakromosfärenkuiperbältetkundts rörkvantdatorkvantmekanikkvantmekanisk sammanflätningkvarkkvark-gluon plasmakvartskvasarkvasipartiklarkärnkrafterkärnreaktionkärnreaktorerkärnvapenlagrange-punkternalaserlenz lagleptonlila linjespektralivljudljusljusabsorptionljusbrytningljushastighetenljuskällorljusutbyteljusårlongitudinell våglorentzkraftenluftmotståndluminiscenslutande planlysdiodlysrörlågenergilampalägesenergilängdkontraktionmachomagnetismmagnuseffektenmarkradarmarkvärmemaskhålmassamasscentrummassdefektmassenhetmassexcessmasstalmateriamaxwell–boltzmannfördelningenmaxwells ekvationermedelvärdetmegaton tntmeissnereffektenmekanikens gyllene regelmerkurius periheliumprecessionmetafysikmetallbindningmetalldetektormetallicitetmeteormeteoritmeteoroidmilankovitch cyklermodern fysikmodernuklidmolmolekylmultiversummymetallmånemätfelmörk energimörk materiamörk nebulosamössbauer-effektennanometertekniknanopartikelnanotekniknationalencyklopedinnaturvetenskapnavigeringneoneutrinoneutrinooscillationerneutroninducerad fissionneutronstjärnanewtonnewtonringarnewtons andra lagnewtons avsvalningslagnewtons första lag (tröghetslagen)newtons gravitationslagnewtons tredje lagnobelpris i fysik 1925nobelpris i fysik 1993nobelpris i fysik 2015nobelpris i fysik 2017nobelpris i fysik 2020normalkraftennorrskennuklidnuklidkartanutida fysiknärsynthetockhams rakknivohms lagoorts kometmolnoregelbunden galaxosmosparapsykologiparbildningpascals princippauliprincipenperiodiska systemetplanck timeplancks strålningslagplanetplanetarisk nebulosaplasmaplasmaplasmaplasticitetpn-övergångpolarisationpolspänningpolär jetstrålepotentialproton-protonkedjanpseudovetenskapqcdqedradiative forcingradioaktivitetradioluminiscensraketekvationenrayleigh-spridningreaktansreflektionreflektionsnebulosarefraktionregnbågerelativ luftfuktighetrelativistisk energirelativistisk jetresistansresistivitetresistivitetresonansroche-gränsenrullmotståndrussells tekannarödförskjutningrörelseenergirörelsemängdrörelsemängdsmomentschwarzschildradiensekulär jämviktsekundsfärisk aberrationsi-enheternasingularitetsi-prefixsi-systemetsjälvinduktansskalärproduktskottsekundslipstreamslumpvisa mätfelsmältvärmesnells lagsolarkonstantensolcellersolenergisolens centrumsolförmörkelsesolkraftverksolvindsolvärmespallationspecifik värmekapacitetspektroskopispektrumspinnspontan fissionstandardavvikelsenstandardmodellenstatisk elektricitetstefan–boltzmanns lagstimulerad emissionstjärnastjärnbildstorhetstrålningstrålningstråloptiksträngteorinstående vågstämgaffelsublimationsupermassiva svarta hålsupernovasupertungt grundämnesuprafluiditetsupraledningsvart hålsvartkroppsvänghjulsystematiska mätfelsåpbubblasäkringsönderfallskedjasönderfallskonstantentemperaturtemperaturspektrumtemperaturstrålningtensortermodynamiktermodynamikens andra huvudsatstermodynamikens första huvudsatsthree mile islandtidtidens riktningtidsdilatationtidsekvationentidvattentidvattenkraftertillämpad fysiktjerenkovstrålningtjernobyltotalreflektiontransformatortransistortransparenstriboelektrisk effekttrippelpunktentrycktryckvattenreaktortröga massantröghettröghetsmomenttunga massantvillingparadoxentyngdtyngdaccelerationtyngdlöshettyngdpunktentyp ii supernovaufoultraljudultraviolett strålningultraviolettkatastrofenunderkylninguniversums åldervakuumvakuumfluktuationervakuumpolarisationvalenselektronvattenburen värmevattenkraftvattenkraftvattenångavektorerverkningsgradvetenskaplig metodwiens förskjutningslagwikipediaviktwimpvindkraftvintergatanvintergatanvirtuell bildvirtuell bildvit dvärgvoltvridmomentv-t diagramvåglängdenvåg-partikeldualitetvågtalvärmeledningvärmemängdvärmepumpvärmepumpvärmeöverföringvätebindningvätelika jonervätskedroppsmodellenväxthuseffektenytenergiångbildningsvärmeångtryckårstidernaåskaädelgasädelgaserögats linsöratöversynthetövertoner (Enda villkor)

---

Om du inte hittar svaret i databasen eller i

Sök i svenska Wikipedia:

Sök i Nationalencyklopedin

   

Sök med Google

   

- fråga gärna här.