Om man slår en golfboll med samma utgångshastighet men med olika vinkel från marken kommer bollen att träffa marken vid samma tidpunkt?
Tack på förhand /Robin D, Valdemarsvik
Svar: Bollen följer en bana som kallas kastparabel, se fråga 13568 . Tiden i luften är helt enkelt den tid det tar för bollen att stiga till maxhöjd och sedan falla till marken igen. Vi delar upp hastighetsvektorn i en horisontell komponent (v*cos(x)) och en vertikal komponent (v*sin(x)), där x är utslagsvinkeln. Tiden i luften 2t blir då
2t = 2*v*sin(x)/g
där x är vinkeln.
Med v konstant kommer alltså tiden att öka som sin(x) från 0 till maxvärdet 2(v/g).
När det gäller golfbollar är det inte realistiskt att som här bortse från luftmotstånd och bollens spinn.
Se fråga 20465 och 16895 för mer om golfslag och golfbollens flykt. /Peter E
Fråga: Fall1: En golf boll träffas av en klubba som roterar med konstant vinkelhastighet, radien r och hastigheten v.
Fall2: Golfbollen träffas av en klubba som har accelererat från hastigheten 0 till v med samma radie som i fall 1.
Vilken golf boll går längst? /Carl C, Hvitfeldtska, Göteborg
Svar: Vad som händer innan träffen har ingen betydelse. Bollens hastighet beror av klubbans hastighet v vid träffen och klubbhuvudets massa, se ekvation (3) i fråga 20465 . /Peter E
Fråga: Hej jag har en fråga gällande golf, jag skjuter en golfboll in i ett nätt hemma för att träna, men kan jag få reda på hur långt bollen skulle a flugit om jag visste: att det är 13 grader vinkel, bollen flyger 260 km/per timme.
De vill säga att det är 0 vind och spikrakt framåt /Emilio M, Internationela engelska, huddinge
Svar: Nej, det är inte så enkelt. Bollens spinn (ger en lyftkraft) och luftmotståndet är helt avgörande för bollflykten.
I fråga 20465 diskuteras bollhastighet och spinn. Se även fråga 16895 och länken golfboll nedan.
Det finns avancerade system som dels mäter bollhastighet och spinn och sedan beräknar bollbanan, se länk 1, men dessa är mycket dyra. /Peter E
Ursprunglig fråga: Hej!
Vi gör vårt gymnasiearbete i fysik och tittar på energiöverföringar i ett golfslag. Mer specifikt undersöker vi själva träffen mellan boll och klubba. Vi har gjort en videoanalys och därigenom fått ut hastigheter för: boll, samt klubba före och efter träff. Vi är dock lite osäkra på hur vi ska räkna med massan för klubban. Ska man göra antagandet att all klubbans massa ligger i klubbhuvudet, eller ska man enbart räkna med klubbhuvudets massa, eller ska man försöka ställa upp en mer avancerad modell? Om inte, hur stort skulle felet tänkas bli, och varför?
Tack på förhand!
Vänliga hälsningar, Emma och Melker /Melker H, Viktor Rydberg Odenplan, Stockholm
Svar: Emma och Melker!
Fysiken bakom golf är mycket komplicerad, men man kan förstå en hel del genom att förenkla problemen. Teorin innehåller ofta fria parametrar som anpassas till mätdata.
I boken The Physics of Golf av Theodore P Jorgensen görs en ganska omfattande analys, men det är inte helt lätt att förstå detaljerna.
Låt oss titta på ert problem som är det enklaste: en central stöt mellan ett klubbhuvud med massan M och en boll med massan m.
Klubbhuvudet har 0 graders loft, så vi har inget spinn. Precis före stöten är klubbhuvudets hastighet V. Efter stöten är klubbhuvudets hastighet u och bollens hastighet är v. Vi antar att stöten är elastisk så att vi inte har några förluster som t.ex. inre friktion pga bollens eller klubbhuvudets deformering. Vid stöten måste vi bevara rörelsemängd och kinetisk energi:
MV = Mu + mv (1)
MV2/2 = Mu2/2 + mv2/2 (2)
Om vi eliminerar u (klubbhuvudets hastighet efter stöten) i (2) med hjälp av (1) får vi för bollens utgånghastighet
v = 2MV/(m+M) = 2V/(m/M + 1) (3)
(I länk 1 finns mer detaljer av härledningen med andra beteckningar.)
Mycket av vad som följer är från kapitel 9 i The Physics of Golf (se ovan).
Om m är mycket mindre än M får vi att v=2V. Detta är alltså den teoretiskt högsta möjliga hastigheten för bollen. Om m=M får vi att v=V (klubbhuvudet är i vila efter stöten). Bollens utgångshastighet är alltså proportionell mot klubbhuvudets hastighet: v = k*V. Konstanten k beror av deformationsförluster (se studskoefficient i fråga 20384 ) och klubbans loft.
Typiska värden för k är 1.46, 1.30 och 1.12 för driver, järnfemma och järnnia, respektive. Klubbhastigheten för en bra spelare är ungefär 45 m/s vilket ger en bollhastighet med driver av 1.46*45=66 m/s. Detta ger en slaglängd på c:a 225 m.
Med ett flexibelt skaft kan man som en hygglig approximation anta att klubbhuvudet vid bollträffen uppför sig som en fri kropp.
Ju större loft en klubba har desto mer spinn får bollen efter träffen. Spinnet ger genom dimplarna och Magnus-effekten en lyftkraft och turbulens som minskar luftmotståndet (se fråga 14113 ). Detta gör att bollen flyger längre.
Spinnet kostar emellertid genom att k blir mindre (se ovan). Detta reflekterar faktumet att en del av den överförda energin går till bollens rotationsenergi.
Parentes: Uttrycket v=2V för ett tungt klubbhuvud kan vi få med ett enklare resonemang. Vid en fullständigt elastisk kollision mellan två objekt bevaras den relativa hastigheten. I ovanstående exempel är relativa hastigheten V (klubbhuvudets hastighet). Efter stöten fortsätter klubbhuvudet med hastigheten V och bollen har hastigheten V i förhållande till klubbhuvudet. Bollens hastighet i förhållande till marken är då v=V+V=2V.
Här är fler frågor som behandlar golf: golfboll . Se även länk 2. /Peter E
Fråga: Hej. Jag skulle vilja ha hjälp med ett matematiskt/fysik problem, som har uppstått i mitt projekt arbete. Jag frågade min lärare men han kunde inte hjälpa mig, så nu vänder jag mig till er på fysikum.
Mitt problem lyder så här:
Jag har varit och mätt min bollflykt vid golfslag och fått reda på utgångsvinkeln, sidospinn, hastighet m.m.
Det jag skulle vilja ha hjälp med är, hur räknar jag ut hur mycket min boll avlänkas ifrån målet (hålet) om man räknar med sidoskruven. Försumma luftmotstånd och sidovind?
Vore jättetacksam för svar och hjälp
Med vänlig hälsning André
/André J, Olympiaskolan, Rydebäck
Svar: Golfbollens flykt är alldeles för komplicerad för fysiken - även om man tar bort osäkerheten hos golfspelaren. I fråga 14113 finns några länkar, framför allt Golf Ball Flight Dynamics . Artikeln ger en relativt komplicerad paramerisering av bollens flykt.
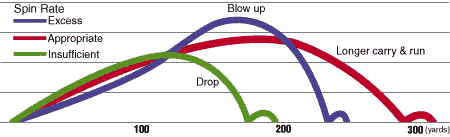
Jag antar du mätt upp parametrarna du nämner med en dator med kamera. Jag skulle tro att det även finns ett program som beräknar hur bollen flyger, men det kan tänkas det bara är en odokumenterad svart låda som man inte lär sig mycket av. Artikeln ovan är då mycket bättre och den innehåller t.o.m. Matematica-kod för beräkningarna. /Peter E
Fråga: Jag undrar när en golfboll uppnår högsta hastighet.
Är det precis efter den lämnar klubbhuvudet i och med att man inte längre tillför energi? Eller är det efter den har lämnat klubbhuvudet i och med att upplagrad lägesenergi i bollen (ihoptryckt) omvandlas till rörelseenergi under en kort tid till dess den har återfått ursprunglig form. /Stefan H
Svar: Golfbollen har högst hastighet just när den lämnat klubbhuvudet. Även om det kan finnas lite komressionsenergi i bollen, så finns det ingen mekanism för att överföra denna till ökad fart på bollen. Energin blir till värmeenergi genom friktion.
Teoretiskt kan man få en liten effekt från golfbollens rotation: rotationen ger en lyftkraft (se fråga 14113 nedan) som får bollen att gå högre. I fallet ner mot marken accelererar den naturligtvis, men hastigheten är ändå lägre än utgångshastiheten vid utslaget. /Peter E
Fråga: Hvorfor kjennes det ut som man treffer en tomat (dvs. at ballen er myk) hvis man treffer den riktig med riktig sving, mens det kjennes ut som om man treffer en hard stein hvis man treffer den feil (feil sving) når det er samme ball og samme kølle man slår med? Regner med at det har noe med fysikklover å gjøre at f.eks kølla fanger opp energien hvis man slår riktig, mens den blir overført til hendene hvis man slår feil. Har prøvd å kikke på nettet og spørre golfproen (treneren) min, men han visste ikke og jeg fant ikke noe på netter. Hadde vært veldig takknemmelig hvis dere kan hjelpe oss med dette (golfproen min vil gjerne også vite svaret).
/Lene B
Svar: Lene! På varje klubba finns en s.k. "sweet spot" där det är tänkt att bollen skall hamna. "Sweet spot" ligger i linje med klubbhuvudets tyngdpunkt. Detta innebär att en träff på "sweet spot" inte förorsakar något vridmoment. Träffar du däremot t.ex. på tån (långt ut på bladet) vrids klubbhuvudet så att klubbytan pekar höger om målet (för en högerspelare). Denna vridning orsakar följande icke önskade effekter
Bollen går till höger
Bollen går kortare eftersom en del av rörelsemängden som skulle överföras till bollen går åt till att rotera klubbhuvudet
Du känner direkt att träffen är fel eftersom klubbhuvudets rotation överförs till händerna via skaftet. Om du håller för hårt i klubban kan det tom göra ont i händerna vid en snedträff.
Två tips för att förbättra ditt spel är dels att träna på bollträffen och dels att hålla så löst som möjligt i klubban. Ett hårt grepp gör att du får mindre fart på klubbhuvudet.
Ursprunglig fråga: Hej! Jag hade tänkt att tillverka en golf-putter som får bollen att rulla direkt vid tillslaget. Gräs som underlag förståss. Är det fysiskt möjligt?
Om JA:
- Hur ska man göra i så fall?
- Hur ska puttern vara utformad?
- Krävs någon speciell slagteknik?
Om NEJ:
- Hur gör man för att minimera det så mycket det bara går?
- Hur ska puttern vara utformad?
- Krävs någon speciell slagteknik?
Tack för svaren! /Joakim G, Sanda Gymnasiet, Huskvarna
Svar: Hej Joakim! Intressant fråga till en entusiastisk golfare men dålig puttare!
Puttning är egentligen mycket enkelt: slå bollen med rätt hastighet i rätt riktning med hänsyntagande till fall på grund av greenens lutning och eventuell vind. Förutom en god teknik (som finslipas med mycket träning) är självförtroende A och O i golf: alla golfare vet att man misslyckas med de flesta slagen med en klubba man inte "tycker om".
Du har helt rätt i att det är mycket viktigt att få bollen att rulla - inte glida - så snart som möjligt. Detta gör man genom att sätta "överskruv" på bollen, dvs så att bollen roterar i samma riktning som den gör när den rullar. Detta är tvärtom mot skruven som åstadkoms med andra klubbor: klubbladets loft (lutningen mot horisontalplanet) orsakar underskruv, vilket en skicklig spelare kan utnyttja till sin fördel, se golfboll . Du vill alltså ha mycket lite loft på en putter (slagytan skall vara nästan 90 grader mot horisontalplanet), annars får du en i de flesta fall icke önskad underskruv.
Överskruven åstadkommes genom att man täffar bollen när puttern är lite "på uppgång" - bollen lite till vänster i stansen och en pendelrörelse hos klubbhuvudet som når sin lägsta punkt lite innan det träffar bollen. Det fordras lite träning för att lyckas med det varje gång.
Vilka egenskaper bör en bra putter ha?
Det bör vara lätt att sikta
Tydlig "sweetspot", vilket är den träffpunkt som inte orsakar rotation hos klubbhuvudet
Lite loft (högst några få grader) så man kan åstadkomma överskruv
Ett handtag som ger en känsla för vart klubbhuvudet pekar (ej cylindersymmetriskt)
Kan man med elementär fysik förstå varför man vill ha överskruv? Ja, jag tror det. Om man träffar bollen exakt på bakkanten med klubbhuvudet vinkelrätt mot och rörelseriktningen parallellt med den önskade riktningen (square hit), så kommer bollen att glida på underlaget till att börja med. Friktionen mot underlaget får bollen att börja rulla efter ett tag (c:a en meter). Från början har bollen endast rörelseenergi, men när den börjar rulla övergår rörelseenergin delvis i rotationsenergi, se fråga 14738 . Bollen saktar alltså in mycket i början av rörelsen. Pröva att slå några 10-metersputtar med samma svinghastighet dels genom att träffa bollen "square" och dels med överskruv. Du kommer att finna att puttarna med överskruv går betydligt längre än puttarna utan skruv. Dessutom blir längden mycket mer konsistent, och det är detta som gör att tekniken är att föredra. Titta på en god puttare (proffs), så skall du se att bollen rullar mycket snart efter träffen, medan bollen vid en dålig träff glider och hoppar vilket ger ett sämre resultat.
Friktionen (och därmed uppbromsningen) är större när bollen glider (och kanske hoppar) än om den rullar fint. Du får därför en mer konsistent putt med en rullande boll.
Kan man inte få överskruv med ett negativt loft på puttern? Nej, det fungerar antagligen inte eftersom man tvingar bollen nedåt in i greenen. Men kanske skulle man kunna pröva lite negativt loft? Såvitt jag vet finns inga sådana putters, och om det fungerade skulle det säkert finnas det.
En sak är i varje fall säker: om du kan konstruera en putter som gör puttningen lättare och dessutom övertyga golfare att den fungerar, så är du miljonär!
PS. Heter du verkligen Green? Då får du kalla puttern Green-putter!
PS2. Lycka till med puttertillverkningen!
Tillägg juni 2017:
Här är en putter med en speciell yta ("microhinges") som påstås ge bollen överskruv:
Fråga: Varför skruvas en läderboll och en plastboll åt olika håll? /Veckans fråga
Ursprunglig fråga: Hej, jag har läst igenom forumet och hittat samma fråga som jag har men det fanns inget svar på frågan. Problemet är det här med att en läderboll som får en skruv medurs skruvas till vänster, och en plastboll som skruvas medurs skruvas till höger. Jag presenterade problemet för min lärare i fysik på LTH och han trodde mig först inte. (Vilket inte personen som gav svar i forumet gjorde heller) Men jag stod på mig varpå han verifierade problemet i verkligheten. Testet utfördes i en gymnasiksal där det inte fanns någon vind. Slutsatsen var att han kunde inte förklara problemet fysikaliskt! Kan du? /Johan J, LTH, Malmö
Svar: Hej Johan!
Nej, jag kan inte förklara problemet. Men jag tror inte heller att olika material skruvar åt olika håll. Tänk t.ex. på en golfboll och en pingisboll. Båda påverkas på samma sätt av underskruv - de påverkas av en kraft uppåt. Detta trots att de har helt olika ytor: golfbollen är knottrig vilket ger turbulent strömning och pingisbollen är slät vilket ger laminär strömning kring bollen. Dessutom finns det ju fotbollar både av plast och av läder, och jag tror en spelare skulle bli mycket förvånad om en ny boll skruvade åt fel håll .
Skruv och lyft hos roterande bollar förklaras av den s.k. Magnuseffekten som bygger på Bernoullis ekvation - högre hastighet hos luften ger lägre tryck (Bernoulli's_principle ). Se även Magnus_effect .
En helt annan effekt är skruvade kast i kricket, men där har man en asymmetri hos bollen och skruven är riktad i samma riktning som asymmetrin - en underskruvad kricketboll avviker i sidled i stället för i höjdled. Se Swing_bowling .
Magnuseffekten är ett fysikaliskt fenomen som uppträder för roterande kroppar. Effekten innebär att en kropp som rör sig genom en fluid (en vätska eller en gas) samtidigt som den roterar accelereras vinkelrätt mot rörelseriktningen, det vill säga att rörelseriktningen "böjs av". Det är den fysikaliska kraft som gör att roterande bollar får så kallad skruv inom olika bollsporter, se Magnuseffekten och fråga 754 .
Video som visar och förklarar Magnuseffekten:
Jag kan inte, trots omfattande sökningar, hitta något väldokumenterat exempel på att materialet i bollen skulle ha någon betydelse. Strukturen på ytan påverkar storleken på Magnus-kraften (dimplarna på en golfboll ökar t.ex. effekten betydligt), men att ett alternativt material skulle ändra kraftens riktning låter inte sannolikt.
Enligt beskrivningen ovan är det plastbollen som uppför sig som väntat. En höger utsida roterar bollen medurs, vilket ger en avvikelse åt höger (den av golfaren fruktade slicen). Kan det vara så att en läderboll är lite asymmetrisk pga en söm (se cricketbollen ovan)? Problemet med denna förklaring är att skruven skulle bero på hur bollen placeras på marken. /Peter E
Fråga: Rörelseenergi för en rullande kula /Veckans fråga
Ursprunglig fråga: Hejsan! Jag har ett problem.
En kula släpps i en kulbana som står placerad på ett bord, vid kanten. Jag har räknat fram att kulan har fått en viss teoretisk energi när den lämnar banan och den har fått en minde energi i verkligheten.
Jag kan anse att luftmotståndet och friktionen inte har någon påverkan och jag har listat ut att det har något med rotationen av kulan att göra, så min fråga är nu. Vart tar energin vägen på sin resa ned för kulbanan?
svara gärna snabbt, arbetet ska lämnas in denna veckan.. /Anna O, Birger Sjöbergymnasiet, Vänersborg
Svar: Ditt problem är inte helt lätt, du får nöja dig med en skiss. Lösningen finns under länk 1, men där på engelska.
Vi börjar med att bortse från kulans rotation. Antag kulans massa är m och dess sluthastighet v. Då gäller enligt energiprincipen (potentiell energi på höjden h = kinetisk energi vid botten):
mgh = mv2/2
dvs
v2 = 2gh
Om kulan inte glider alls kommer den att sättas i rotation. Om tyngdpunktens hastighet i detta fallet är u, kommer vinkelhastigheten w att vara u/r där r är kulans radie. (Du får detta resultat eftersom den del av kulan som rör vid kulbanan har hastigheten 0 i förhållande till banan - kom ihåg, inget glid!).
En homogen kulas tröghetsmoment ges av J = 2mr2/5 (Tröghetsmoment#Exempel ) och rotationsenergin är Jw2/2.
Vi adderar translations-kinetiska energin och rotationsenergin och får
Detta är klart mindre än 2gh som vi fick ovan eftersom ju en del energi går till kulans rotationsenergi. Förhållandet u/v blir ungefär 0.85, alltså 15% lägre hastighet än en kula som glider perfekt och inte roterar.
Förhållandet mellan rotationsenergi och translationsenergi blir enligt ovan
(1/5)/(1/2) = 2:5.
Tillägg om puttning i golf
Golfspelare som puttar bra ser till att slå till bollen med en något uppåtgående rörelse för att bollen om möjligt skall börja rulla omedelbart. Om man slår till bollen helt centralt kommer bollen att glida ett tag på gräset. Friktionen kommer efter ett tag att få bollen att rulla, men rotationsenergin måste tas från rörelseenergin. Bollen bromsas alltså upp för att den skall kunna få rotation. Det visar sig att längden på puttarna blir mycket mer konsistent om man kan få bollen att rulla direkt vid tillslaget.
Tekniken att få överspinn på bollen direkt vid tillslaget används även t.ex. i biljard då man oftast slår till bollen ovanför ekvatorsplanet vilket får bollen att börja rulla omedelbart.
Fråga: Hur räknar man ut optimal utgångsvinkel vinkel för en golfboll? /Veckans fråga
Ursprunglig fråga: Om jag slår en golfboll med en driver kommer den
att lämna peggen i med en viss hastighet och vinkel.
Jag vet att klubbans hastihet är ca 190km/h och boll hastigheten ca 280 km/h utgångsvinkeln är ca 17 grader
Hur räknar man ut optimal (max) höjd för en golfboll?
Vilka parametrar måste man känna till? /Roland A, Båstad
Svar: Problemet är på grund av luftens inverkan mycket mer komplicerat. En golfboll rör sig inte alls i en kastparabel eftersom luften spelar mycket stor roll. För ett mellanjärn är banan sedd från sidan närmast hypotenusan av en rätvinklig triangel.
Spinnet och dimplarna (de små groparna) på en golfboll minskar för det första luftmotståndet (genom turbulens) och ger dessutom upphov till en lyftkraft (genom den sk Magnus-effekten). Bilden (från nedanstående länk Flight Dynamics of Golf Balls) visar bollbanan för olika spinn. Det är uppenbart viktigt all få lagom spinn på bollen!
Fråga: Hej!
Jag skulle vilja vet hur en golfboll kan få en högre hastighet än vad svinghastigheten på golfklubban är? /Micke S, Roslagsskolan, Norrtälje
Svar: Kastar du en elastisk boll mot en vägg med hastigheten v, studsar den tillbaka med hastigheten -v. Fartförändringen blir alltså 2v. Slår man mot en golfboll med farten v med en tung golfklubba, blir golfbollens fartändring 2v. Detta är alltså ren mekanik. Här har vi antagit helt elastiska kollisioner, vilket ju inte är alldeles sant. /KS
Fråga: En golfboll slås med 2 olika klubbor.
Fall 1: Slås med en klubba som har 0 graders vinkel och träffar
vinkelrätt mot bollen.
Fall 2: Slås med en klubba som har 45 graders vinkel.
Klubbhuvudet antas ha samma fart och vikt vid träffögonblicket i båda fallen.
Frågan är nu om båda bollarna har tillförts lika mycket energi
(alla energier totalt) eller om det är olika.
Mätögonblicket skall vara exakt då bollen
lämnat klubban.
Anledningen till frågan är att det känns mycket lättare(mindre motstånd)
att slå med
en vinklad klubba kontra en som är rak.
M.a.o det känns som det finns mera fart(energi) kvar efter träffen med
vinklad klubba och därmed bör man inte 'lämnat' av
lika mycket energi till bollen. /Bertil J, Östersund
Svar: Vid anslagsögonblicket påverkas bollen av en kraft vars riktning är
vinkelrät mot klubbladet. Storleken på den kraften är proportionell
mot klubbans hastighetskomposant i den riktningen. I fall 2 blir den
kraften sqrt(0.5) mindre än i fall 1. Bollens sluthastighet blir
mindre med samma faktor. Faktorn för rörelseenergin blir 0.5
(kvadraten på hastigheten). Så dina iakttagelser är nog riktiga. /KS
Fråga: Varför är det gropar i golfbollar? Och var kan man få mer info?
/Viktor F, Wieselgrensskolan, Helsingborg
Svar: Kring en boll med hög hastighet råder så kallat turbulent
flöde. Då är det en massa små luftvirvlar kring bollen. De funkar
som små "kullagerkulor" som minskar friktionen mot luften. Luftmotståndet
är lågt. Vid en viss lägsta hastighet ändras strömningsförhållandena
drastiskt. Virvlarna försvinner, och flödet blir laminärt, och
bollen får kontakt med luften. Luftmotståndet ökar.
De små kratrarna på golfbollen gör att denna övergång sker vid en
lägre hastighet, alltså bollen kommer gå mycket längre med lågt
luftmotstånd. En skicklig golfspelare kan slå golfbollen 250 m.
Med en slät boll skulle han bara nå 100 m.
Detta lär ha upptäckts genom att vissa golfspelare hade en
"turboll", som de inte ville skiljas från. Förr i världen
var golfbollarna släta, men en mycket använd golfboll var
alldeles knottrig efter alla slag. Den slog man längre med.
Vidskepelse? Nej, fysik!
Fråga: Vilka krafter påverkar en "skruvad" boll så att den ändrar riktning? /Johanna H, Vadsbogymnasiet, Mariestad
Svar: Det är ingen lätt fråga att ge ett kort och uttömmande svar på. Effekten kallas för magnuseffekten. I många böcker finns det missvisande "förklaringar" till fenomenet. Se länk 1 för en avancerad beskrivning av magnuseffekten och aerodynamisk lyftkraft för en flygplansvinge. I Magnus_effect finns en parametrisering av storleken på lyftkraften.
Låt oss i den följande diskussionen anta att vi har slagit en
underskruvad boll. Tänk på bordtennis eller golf! Bollen får då en uppåtriktad
kraft på grund av rotationen.
En viktig princip i strömningslära är att luften häftar vid bollen. Vid bollens yta
finns alltså ett tunt luftlager som följer med bollen.
Det är rätt lätt att övertyga sig om att luften strömmar fortare ovanför än under bollen.
(Vi betraktar luftens hastighet relativt bollen.)
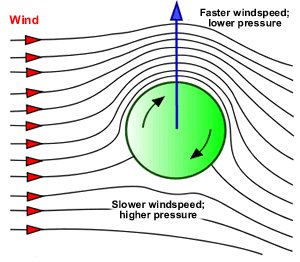
Luften som går snabbare över bollen måste accelereras. För detta krävs en tryckskillnad. Trycket
är alltså lägre rakt över bollen än långt bort från bollen. Med samma argument visar
man att trycket är högre strax under bollen. Tryckkrafterna påverkar alltså bollen uppåt! Se nedanstående figur.
Ett annat sätt att se problemet är att bollens rotation "drar isär" luften på ovansidan och "trycker ihop" luften på undersidan. Vi får alltså lågt tryck på ovansidan och högt tryck på undersidan. Denna tryckskillnad ger upphov till en lyftkraft.
Experiment: Be en kamrat slå en bordtennisboll hårt med mycket underskruv. Stå vid sidan och studera bollbanan. En golfboll beter sig likadant men är svårare att studera.
.
Sök i svenska Wikipedia:
