Det står att en bil kör över ett backkrön med konstant hastighet. På ett säte inne i bilen ligger ett paket. Hur ska man veta vilka krafter som verkar på paketet och varför är det så att tyngdkraften är större en normalkraften på paketet?

Sen undrar jag också hur man ska räkna ut den hastigheten bilen behöver för att paketet ska lätta från sätet precis på toppen av backen. Vad innebär det egentligen att paketet lättar från sätet? Att den åker av? Paketets massa är 2,55 kg. hastigheten är 12m/s och radien på backkrönet har radien 80 m.
/Maria O, Borgarskolan, Malmö

Svar:
Vi har flera svar om acceleration i cirkelrörelse t.ex. fråga 18916 . Frågan finns dessutom i pluggakuten, länk 1, så det blir kortversionen:

Nedåt verkar tyngdkraften mg. Detta kan du se som en acceleration g uppåt. Cirkelrörelsen ger en acceleration nedåt

a = -v²/R = -12²/80 = -1.8 m/s² = -1.8/9.81 g = -0.18 g

så netto g som paketet utsätts för är (1-0.18)g = 0.82g

Vid vilken hastighet är netto g noll?

mg = mv²/R

dvs

v =sqrt(gR) = sqrt(9.81*80) = 28 m/s

Problemet är att även bilen flyger i luften om den inte sitter fast i skenor som en berg-och-dalbanevagn!
/Peter E

Nyckelord: centrifugalkraft [15]; g-krafter [18];

1 http://www.pluggakuten.se/forumserver/viewtopic.php?pid=216115

Har problem med följande:

En framtida rymdstation ser ut som ett gigantiskt cykelhjul. Invånarna lever inne i på avståndet 900 m från axeln. Om rymdstationen roterar så att centripetalaccelerationen där är 9.82 m/s^2, så kommer invånarna att känna samma tyngd som på jorden. Hur lång rotationstid måste ha då? Figuren visar att invånarna har sina fötter mot yttersidan av stationen. Varför måste det vara så?

Jag har beräknat att dess rotationstid är 60.2 sekunder men förstår verkligen inte varför invånarna har sina fötter mot yttersidan av stationen.

Om någon skulle kunna förklara detta vore jag grymt tacksam!
/John N, Komvux Stockholm, Stockholm

Svar:
Acceleration in mot rotationscentrum (masscentrum) ges av

a = v²/R

där v är rotationshastigheten för periferin och R är radien. Om denna sätts lika med g får man lätt v=94.0 m/s. Tiden för ett varv blir

2pR/v = 60.2 s

precis som du kommit fram till.

För att kunna diskutera krafterna får vi först bestämma vilket koordinatsystem vi vill ha. Vi väljer ett system som är fixt i förhållande till rymdstationen. Eftersom detta system roterar är det inte ett inertialsystem utan ett accelererat system. Vi kan då använda oss av den fiktiva centrifugalkraften som är riktad ut från rotationscentrum. Det är denna kraft som tvingar invånarna att ha fötterna mot yttersidan. Det är inte konstigare än att australiensarna har fötterna i en riktning motsatt oss eftersom jorden är rund.

Alternativt resonemang är att acceleration i en riktning (in mot centrum) är ekvivalent med ett gravitationsfält i motsatt riktning (ut från periferin). Detta är Einsteins ekvivalensprincip.

Se även fråga 15272 . Se fråga 12037 för en diskussion om varför man inte använder denna konstruktion med en roterande rymdstation.
/Peter E

Nyckelord: centrifugalkraft [15]; rymdfärder [23];

Svar:
Maria! Du har rätt i att man klarar sig utmärkt utan centrifugalkraft. Centripetalkraften som kan orsakas av spänningen i ett snöre, ett magnetfält, ett elektriskt fält eller ett gravitationsfält tvingar partikeln att accelereras in mot centrum så att den får en cirkelbana. För att åstadkomma en acceleration a hos en kropp med massan m erfordras en nettokraft F enligt F=m*a. Om du inför en lika stor utåtriktad kraft blir det ingen nettokraft och ingen acceleration.

Du kan införa en centrifugalkraft om du väljer ett koordinatsystem som rör sig med din partikel. Detta är rimligt för att förklara vad som händer inne i en bil som går genom en kurva. För subatomära system är detta val av koordinatsystem inte särskilt praktiskt.

I kvantmekanik använder man sig dessutom över huvud taget inte av krafter utan potentialer. Dessutom kan man inte se elektronerna i atomer som små laddade partiklar som rör sig i banor runt atomkärnan,se fråga 13733 .

Se vidare en detaljerad utläggning om centrifugalkraft i fråga 15272 .
/Peter E

Nyckelord: centrifugalkraft [15]; kvantmekanik [30]; centripetalkraft [11];

Svar:
Alina! Bra fråga! Man blir ju yr i en karusell, så varför inte på jorden som ju är som en stor karusell som gör ett varv på 24 timmar.

Främsta anledningen är att jordens rotation är ganska långsam: ett varv tar 24 timmar. Det som gör att du blir yr är att kraften som verkar på dig, resultanten av jordens tyngdkraft plus karusellens centrifugalkraft, ändras snabbt med tiden. Detta påverkar balanssinnet eftersom vad som uppfattas som upp och ner varierar med tiden.

Ett ytterligare skäl är att jordens rotation sker runt en axel som går genom jordens centrum. Centrifugalkraften är då riktad utåt vinkelrätt mot rotationsaxeln. Den resulterande kraften av centrifugalkraft+tyngdkraft kommer då att peka i en konstant riktning i förhållande till jordytan.

Se länk 1 för en längre, engelsk version av svaret. Fråga 15272 behandlar krafter om man åker karusell. I fråga 14923 räknas det ut hur mycket lodlinjen avviker från riktningen mot jordens centrum pga jordens rotation.
/Peter E

Nyckelord: centrifugalkraft [15];

1 http://www.madsci.org/posts/archives/1999-10/939275753.Ns.r.html

Ursprunglig fråga:
Varför flyger man utåt om man åker fortare i en karusell som ser ut som Kättingflygaren på Gröna Lund?
/Johanna

Svar:
Johanna! Karusellen ser ut som den på bilden nedan från Chair-O-Planes .

För att sitsarna med (eller utan) passagerare skall röra sig i en cirkelbana erfordras en kraft riktad mot centrum. Denna s.k. centripetalkraft ges av

F_r = mv²/r

Om rotationshastigheten v ökar ökar radien r och vinkeln a mellan vertikalplanet och kättingen minskar för att centripetalkraften skall öka, se figuren nedan.

Det är två krafter som tillsammans orsakar nettokraften F_r (de två steckade krafterna i figuren):

1 Spänningen i upphängningskedjan F_F riktad snett uppåt i kedjans riktning.

2 Tyngdkraften F_G = mg riktad rakt nedåt.

Från triangeln med F_F och F_r får man

tan a = F_r/F_G

dvs

F_r = tana*F_G = tana*mg

Men enligt ovan var ju

F_r = mv²/r

dvs

mv²/r = tana*mg

eller

v² = r*tana*g

Vi ser för det första att sambandet inte beror av massan m.

Om avståndet från rotationscentrum till upphängningspunken är r₀ blir radien

r = r₀ + l*sina

där l är kedjans längd. Vi får alltså till slut sambandet

v² = (r₀ + l*sina)*tana*g

Vi ser att om hastigheten v ökar så måste även vinkeln a öka. Ekvationen ovan är svår att lösa exakt, men i appleten under länk 2 kan man variera parametrarna och se vad som händer.

Se Slagkraft - Naturvetenskap på Liseberg för mer om Kättingflygaren och andra Liseberg-attraktioner.

Se även Kättingflygare .

Nyckelord: centrifugalkraft [15]; kraft [12]; *nöjesparksfysik [12]; pendel, konisk [2]; centripetalkraft [11];

1 http://www.walter-fendt.de/ph14d/karussellmath.htm
2 http://www.walter-fendt.de/ph14se/carousel_se.htm

Så vitt jag förstår finns det dels en acceleration in mot cirkelns mitt, och också en centrifugalkraft. Vilken riktning har centrifugalkraften? Finns det även en friktionskraft som gör att man hålls kvar och inte slungas av karusellen?
/Axel K, Fyrisskolan, Uppsala

Svar:
Hej Axel! En bra och besvärlig fråga. Besvärlig för att man pratar om en väldig massa krafter hit och dit. Det fall du frågar efter - att du sitter still på karusellen - är inte så svårt om man bara resonerar korrekt.

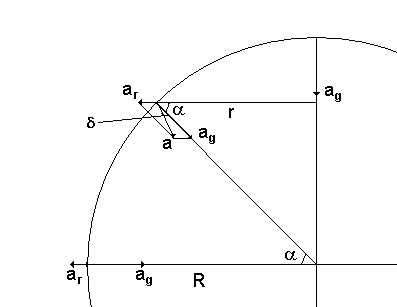
Det viktiga är vilket koordinatsystem du vill arbeta i. Det är helt upp till dig att välja detta - normalt väljer man ett system som gör problemet så enkelt som möjligt. Det finns två koordinatsystem som är av större intresse än andra:

1 Ett system där du är i vila. Eftersom detta måste röra sig i en cirkel med karusellens rotation, så är detta ett accelererat system (icke inertialsystem).

2 Ett system utanför karusellen. Detta system befinner sig i vila (vi kan bortse från jordens rörelse) och är alltså ett inertialsystem (icke accelererande system).

I båda systemen påverkas du av en gravitationskraft m*g riktad nedåt. Denna balanseras av en motkraft från golvet. Så vertikalt är nettokraften noll och alltså ingen acceleration.

I system 1 påverkas du av en centrifugalkraft riktad ut från centrum (systemet är ju inget inertialsystem). Eftersom du befinner dig i vila i förhållande till system 1 behövs en kraft som kompenserar centrifugalkraften. Det är friktionskraften eller den motkraft som bänken ger.

I system 2 rör du dig i en cirkel, dvs du accelereras hela tiden in mot karusellens centrum. Kraften som åstadkommer accelerationen är samma friktionskraft vi hade i system 1, men eftersom system 2 är ett inertialsystem så finns ingen centrifugalkraft som kompenserar friktionskraften. Friktionskraften (riktad mot karusellens centrum) orsakar en acceleration som får dig att beskriva en cirkelrörelse.

Svenska Wikipedia säger om centrifugalkraft (centrifugalkraft ):

Centrifugalkraft är en term vilken kan referera till två olika krafter vilka är relaterade till rotation. Båda är riktade ifrån rotationscentrum men de objekt vilka de verkar på är olika.

1 En reell eller "reaktiv" centrifugalkraft uppträder som en reaktion på en centripetal acceleration som verkar på en massa. Denna centrifugala kraft är till storleken lika med den centripetala kraften men riktad från rotationscentrum och verkar på det objekt vilket orsakar den centripetala accelerationen.

2 En pseudo eller "fiktiv" centrifugalkraft uppträder när en roterande referensram används for analys. Accelerationen (den sanna) av referensramen ersätts med en (fiktiv) centrifugalkraft som påverkar alla objekt och är riktad från rotationscentrum.

1 är alltså kraften (reaktionskraften till centripetalkraften) som verkar utåt på din hand om du snurrar en tyngd som sitter på ett snöre.

2 är den fiktiva kraften man känner om man befinner sig inne i ett system som utför en cirkelrörelse.

Hoppas detta var begripligt. Kom ihåg att det är endast i icke-inertialsystem (accerererade system) du behöver involvera fiktiva krafter som tröghetskrafter och centrifugalkrafter.

Se diskussion under länk 1 och fråga 3160 där karusellåkaren inte sitter stilla.
/Peter E

Se även fråga 3160

Nyckelord: centrifugalkraft [15]; *nöjesparksfysik [12]; centripetalkraft [11];

1 http://fragelada.fysik.org/forum/display_message.asp?mid=769

Ursprunglig fråga:
Om man står på marken bör man se till att hålla sin egen tyngdpunkt på en linje genom jordens tyngdpunkt och sina egna fötter, annars trillar man ikull. Men, hur muycket påverkar den centrifugalkraft som jordrotationen ger upphov till detta? Inte alls om man står på ekvatorn eller nord(syd)polen. Men i Skåne! Hur många grader (eller fraktioner av en grad) måste man luta sig "inåt" (dvs mot norr) för att inte falla ikull pga centrifugalkraften?
/Jon L

Svar:
Jon! Det är en helt omärkbar effekt och det är knappast någon risk att man trillar, men låt oss som en övning räkna ut hur stor effekten är. Vi antar att jorden är klotformad och homogen med radien R. Den enda effekt vi tar hänsyn till är jordens rotation, vi bortser alltså från tillplattningen. Vi inför några beteckningar (se figuren):

a_g = 9.822 m/s² tyngdaccelerationen från jordens dragningskraft, se länk 1
a_r accelerationen pga jordens rotation
a den resulterande tyngdaccelerationen
R = 6.37*10⁶ m jordradien
a latituden
w = 2p/(24*60*60) = 72.7*10^-6 s^-1 vinkelhastigheten för jordens rotation

Vid polerna och ekvatorn är det ingen avvikelse i vinkel mellan a och a_g (precis som du säger) medan det för medelhöga latituder är en avvikelse så att det är en liten "uppförsbacke" när man går norrut. Om du så vill kan du förstå detta som att "centrifugalkraften" försöker hindra dig att gå närmare rotationsaxeln.

Låt oss börja med att se vad som händer vid ekvatorn. Rotationshastigheten ges av

v = R*w = 6.37*10⁶*72.7*10^-6 = 463 m/s

Accelerationen pga rotationen blir

a_r = v²/R = R*w² = 6.37*10⁶*(72.7*10^-6)² = 0.0337 m/s²

Tyngdaccelerationen vid ekvatorn blir alltså

a_g - a_r = 9.822 - 0.0337 = 9.788 m/s²

Accelerationen pga rotationen vid latituden a blir

a_g = r*w² = R*cosa*w²

Tillämpning av cosinuseoremet på triangeln a_g, a_r, a ger

a² = a_g² + a_r² -2a_ga_rcos(a)

Den andra termen i högra ledet är mycket liten så vi kan försumma den. Vi får då

a = a_g(1 - 2Rw²cos²a/a_g)^1/2 = a_g(1 - Rw²cos²a/a_g) = a_g(1 - 0.0337*cos²a/9.822)

a = a_g(1 - 0.00343*cos²a)

Lodlinjens avvikelse från riktningen mot jordens medelpunkt d kan beräknas genom att vi tillämpar sinusteoremet på triangeln:

sind/a_r = sina/a

sind = a_r*sina/a = Rw²*cosa*sina/a = Rw²*sin2a/2a

Från detta uttryck kan vi se att avvikelsen är maximal för a=45^o och noll för a=0^o och a=90^o.

Eftersom a är approximativt lika med a_g och eftersom vinkeln är liten (sind = d) får vi

d = Rw²*sin2a/2a_g = 0.0337*sin2a/(2*9.822) = 0.00172*sin2a

d i grader blir

d = 180*0.00172*sin2a/p = 0.0985*sin2a grader

Från detta kan vi se att lodlinjens maximala avvikelse (vid latituden 45^o) är c:a 0.1^o.

Nyckelord: tyngdaccelerationen [16]; centrifugalkraft [15]; jordens rotation [22];

1 http://en.wikipedia.org/wiki/Acceleration_due_to_gravity

Ursprunglig fråga:
Håller på med centralrörelse och tyckte då att det skulle vara kul att räkna lite på vilka farter som är möjliga i en doserad kurva utan att bilen får sladd. Gjorde en hel del förenklingar. Införde följande krafter tyngdkraften och normalkraften och en friktionskraft mellan vägbanan och däcken. Friktionskraften bör väll vara riktad innåt i kurvan men längs vägbanan? Friktionskraften får då en vertikal komposant som är riktad neråt och alltså samverkar med tyngdkraften, vilket känns lite märkligt. Kan det vara så? Hur löser man den här typen av problem?
/Marianne A, Ehrensvärdska, Karlskrona

Svar:
Marianne! Att räkna med friktion är ganska besvärligt eftersom det är svårt att veta vad friktionskoefficienten är. Det väsentliga i ditt problem är väl ändå doseringen, dvs vägens lutning i en kurva. Låt oss först definiera några storheter.

bilens massa = m
tyngdaccelerationen = g
normalkraften = N
doseringsvinkel = a
bilens hastighet = v
kurvradie = r

Bilen påverkas av två krafter: normalkraften N från vägbanan och mg från tyngdkraften. Om vi sätter samman dessa får vi en resulterande horisontell kraft R mot vägens krökningscentrum. Det är denna kraft som ger den acceleration som får bilen att röra sig med en cirkelbana. Accelerationen är

mv²/r = R = mg*tana

Vi får alltså sambandet

v² = r*g*tana

För en viss given hastighet och kurvradie kan vi alltså med detta uttryck beräkna den optimala doseringsvinkeln. Bilen kan naturligtvis även ta kurvan med en annan hastighet, men då behöver vi friktion för att hålla den kvar på vägen. Om hastigheten är större än v får du mycket riktigt en vertikal komposant. Detta gör att normalkraften ökar, dvs bilen "trycks" mot vägbanan.

Vi har, eftersom vi betraktar bilen från vägens perspektiv, inte infört någon centrifugalkraft , utan vi har en resulterande kraft R som ger en centripetalacceleration.

Nyckelord: centrifugalkraft [15];

Svar:
Hej Zen! Centralrörelse är om du knyter fast en boll i ett snöre och låter den snurra runt. Du känner då en dragkraft i snöret. Denna dragkraft påverkar bollen, och kallas då centripetalkraft, så att bollen tvingas röra sig i en cirkelbana. Kom ihåg att Newton lärt oss att en kropp som inte påverkas av en kraft fortsätter i vila eller likformig rörelse (rakt fram), se Newtons rörelselagar .

Centrifugalkraft är vad en myra skulle känna inne i bollen. Det är en fiktiv (icke existerande, men det kan den stackars myran inte veta) kraft som orsakas av den acceleration bollen ges av centripetalkraften.
/Peter E

Nyckelord: centrifugalkraft [15];

1 http://sv.wikipedia.org/wiki/Centripetalkraft
2 http://sv.wikipedia.org/wiki/Centrifugalkraft

Jag har försökt att läsa in mig på detta på en sida som heter: www.rollrite.co.uk för att kunna ge ett överygande/förklarande svar för mina spelare.
/Gert F, Vännäs Gymnasium, Vännäs

Svar:
Gert! Jag kan nästan ingenting om bowling. Har provat ett par gånger, och efter ett par tur-strikes till att börja med blev det mest rännan .

Definitionen på Mass bias är: The term Mass Bias refers to the fact that the center of mass of a bowling ball is not located directly under the pin of the ball. Having a Mass Bias causes the center of gravity (CG) mark of a ball to move away from the pin, resulting in a pin-out ball. (www.morich.net/deTerminator/).

Eftersom man inte även definierar "pin" så är definitionen nästan meningslös.

Följande är helt amatörmässiga spekulationer:

Jag antar att klotet glider en stund på banan, och att friktionen får det att rotera mer efter hand. Det som bestämmer hur mycket klotet glider är i första hand friktionen (ytornas beskaffenhet) och tröghetsmomentet hos klotet. Såvitt jag förstår är massan i ett bowlingklot inte klotsymmetrist fördelad. Detta betyder att klotet får olika tröghetsmoment för olika rotationsaxlar. Klotet uppför sig allså lite olika beroende på hur det är orienterat vid utkastet. Jag misstänker att begreppet har något att göra med detta.

Det ligger alltså antagligen något i begreppet Mass bias, se emellertid nedanstående kommentarer:

Jag kan lite mer om golf, emellertid. På min "trä"-trea står det 'Calibrated technology' och 'Trajectory orientated'. Det låter naturligtvis som något man behöver för att slå långt och rakt. Det är emellertid i sammanhanget fullständiga nonsenord som bara är till för att man skall köpa klubban. Det gjorde ju jag, även om anledningen var att jag tyckte texten var så utomordentligt fånig! Klubban fungerar emellertid ganska bra, så den är kanske kalibrerad (kalibrera: anpassa eller ställa in (ngt) efter i förväg fastställda mått, NE).

Ännu ett exempel på termer och uttryck man använder (missbrukar) i speciella sammanhang: jag brukar reta bilskollärare och golfinstruktörer med att centrifugalkraften inte finns! Man kan tydligt se en ängslan i ögonen när de plötsligt förlorat något som dom byggt upp hela sitt liv på!
/Peter E

Nyckelord: centrifugalkraft [15]; *idrottsfysik [42];

Ni säger att den kraft som verkar på människan i det simulerade gravitationsfältet är centrifugalkraften. Jag trodde att den slopades för ett antal år sedan, eftersom den inte är någon riktig kraft. Vad som trycker människan nedåt är ju hennes egen tröghet, samt centriPETALkraften, som verkar i tangentens riktning.
/Johan L, Sundsta-Älvkullegymnasiet, Karlstad

Svar:
Det är helt riktigt att centrifugalkraften inte finns utifrån sett. Ofta är det ändå praktiskt att använda så kallade fiktiva krafter i accelererade system. Centrifugalkraften är ett exempel, corioliskraften är ett annat. När ett flygplan accelererar på startbanan trycks man tillbaka i stolen som om man påverkas av en (fiktiv) kraft. För ytterligare diskussion, sök på fiktiv i denna databas.

Centripetalkraften är vinkelrät mot tangenten.
/KS

Se även fråga 4878

Nyckelord: centrifugalkraft [15];

Tänk er en stor skiva, lagom stor och snurrar lagom fort för att experimentet skall fungera. I centrum sitter en person på skivan. På periferin sitter en person på skivan. Utanför skivan i skivans plan, klockan 3 finns ytterligare en person. Högt ovanför skivans centrum finns ytterligare en person.

Personen på periferin avlossar en kula (som lyser) mot personen i centrum. 1) Kommer personen i centrum att träffas av kulan? 2) Kommer han att "se" kulan hela tiden? 3) vad ser personen i klockan tre? 4) vad ser personen ovanför skivan? 5) vad blir skillnaden om skivan är väldigt stor, snurrar väldigt fort och kulan är en ljusstråle?
/Göran H

Svar:
Den roterande skivan är ett exempel på ett system som inte är ett inertialsystem, det vill säga att det inte är ett system i likformig rörelse. Där uppträder fenomen som tycks kräva verkan av nya krafter som kallas "fiktiva krafter", som i detta fall kallas corioliskrafter. För betraktaren ovanför skivan verkar allt normalt, inga nya krafter behövs. För att kulan ska träffa personen i centrum, måste kulan skickas rakt mot den personen, inget konstigt med det. Siktar personen på periferin rakt på centrum, kommer inte kulan gå rakt mot centrum, rotationen finns ju med. För personerna på skivan verkar kulan påverkas av en kraft (corioliskraft) som böjer kulans bana. Personen ovanför skivan har en helt annan uppfattning, man har helt enkelt siktat fel.

De fiktiva krafterna (centrifugalkraft, corioliskraft) behövs egentligen inte alls, men de kan ha praktisk användning i vissa fall.Vi har inte i detalj svarat på dina frågor, men vi har beskrivit den grundläggande fysiken. Den sista frågan kräver behandling med speciell relativitetsteori, och det går vi inte in på här.
/KS

Se även fråga 8262 och fråga 9698

Nyckelord: inertialsystem [6]; centrifugalkraft [15];

Svar:
För att reda ut detta så börjar vi från början: Vad är en kraft? Jag brukar lite tillspetsat säga att “Krafter finns inte“. Vad som vi ser i naturen är att olika kroppar påverkar varandra: Vi sparkar iväg en fotboll, vi stänger en dörr, två magneter attraherar varandra, jorden accelererar simhopparen som faller osv. Allt detta är exempel på mekanisk påverkan av en kropp på en annan. För att beskriva denna mekaniska påverkan inför man i fysiken kraftbegreppet. Alla krafter är alltså “bara teoretiska“. Krafter finns alltså bara i den fysikaliska teorin (eller modellen om du så vill). När en kropp påverkas av en annan kropp, vilket vi beskriver med en kraft så deformeras eller accelereras kroppen. Ofta sker naturligtvis bägge sakerna samtidigt. Tänk på en tennisboll som slås iväg med ett racket. För att beräkna accelerationen använder man Newtons lag: F =ma. En fråga som då genast uppstår är: Relativt vilket system ska accelerationen beräknas?

Fundera: En kropp ligger still på jorden. Ligger den still i förhållande till solen? Det är väldigt svårt att säga vad som "ligger still". För att Newtons accelerationslag ska gälla måste accelerationen beräknas i förhållande till ett system som "ligger stilla". Men ibland tycker man det är lämpligt att säga att en kropp rör sig relativt något som inte "ligger stilla". Tänk på en karusell. Du sitter still i karusellen och vill räkna ut de krafter som verkar på dig. Man kan då "låtsas" att Newtons kraftlag gäller även om din rörelse relateras till den roterande karusellen, men man måste då införa en ny typ av krafter nämligen tröghetskrafter. Centrifugalkraften är en sådan tröghetskraft. Dessa krafter beskriver inte påverkan mellan kroppar på samma sätt som "riktiga krafter". Använder man tröghetskrafterna korrekt så ger det precis samma resultat som om man endast räknar med "vanliga" krafter.

Varning! Det är en stor risk att man blandar ihop vanliga krafter med tröghetskrafter och jag tycker nog att man i de flesta fall bör hålla sig till de vanliga krafterna. Men det finns några problemställningar där tröghetskrafter är naturliga.

Problem: Som ett test på om du kan använda tröghetskrafter korrekt får du här ett problem. Vad skulle tyngdaccelerationen vara vid ekvatorn om jorden inte roterade? Räkna ut detta både med och utan tröghetskrafter!

Nyckelord: centrifugalkraft [15];

Ursprunglig fråga:
Att det blir flod på den sidan av jorden som är vänd mot månen pga dess dragningskraft är väl förhoppningsvis rätt uppfattat. Men samtidigt blir det ju flod på andra sidan av vårt kära klot, alltså den sidan som är vänd bort från månen. Förklaras det också utav månens dragningskraft?
/Hans F, Kvarnbyskolan, Mölndal

Svar:
Låt oss börja med att definiera tidvatten: Tidvatten (ebb och flod) är periodiska rörelser i havet som beror på månens och solens dragningskraft. Verkan av månens dragningskraft är dominerande eftersom månen befinner sig så nära jorden. Solens inverkan är att förstärka tidvatteneffekten när solen, jorden och månen ligger i en linje och försvaga den när vinkeln solen-jorden-månen är 90^o.

Problemet med de två bulorna är en klassisk besvärlig fråga eftersom man använder två till synes olika modeller som förklaring. Mer om detta nedan; här är först den förklaring jag föredrar från den engelska versionen av Wikipedia, Tide , där även bilderna nedan kommer ifrån:

Titta på den översta bilden. En partikel på jordytan närmast månen påverkas av en kraft som är lite större än en kraften på en partikel i centrum, som i sin tur påverkas av en större kraft än en partikel på frånsidan eftersom gravitationskraften avtar som 1/r². I stället för krafter kan vi uppfatta pilarna som accelerationer som orsakas på en massa m (F=ma). Om vi subtraherar accelerationen i jordens masscentrum får vi kvar accelerationer enligt den nedre figuren: på närsidan en liten rest riktad mot månen och på bortre sidan en rest riktad från månen. Denna subtraktion innebär att vi väljer ett koordinatsystem som är i vila i förhållande till jordens masscentrum.

Låt oss föreställa oss jorden med hav överallt. De resulterande krafterna kommer då att lyfta havet med ett litet belopp h så att mgh (m är massan av, säg, en cm³ vatten) är lika med den resulterande tidvattenskraften. Höjden h är c:a 0.54 m och, om man även tar med solens maximala påverkan, 0.79 m. När väl denna justering av havsytans form skett, råder jämvikt och jordens form är fix.

Tidvatten kan emellertid på vissa platser vara upp till 10 m. Anledningen till denna stora avvikelse är att jorden bara delvis är täckt av hav och att kustlinjerna kan ge en stor förstärkning av effekten, se Lectures on tides . Det kan dessutom förekomma resonansfenomen (se nedan) eftersom tidvattenskrafterna är periodiska. I Tide#Phase_and_amplitude finns en karta över fas och amplitud his tidvattnet över hela världen.

Om det inte fanns något vatten på jorden skulle jordens form ändå anpassa formen efter tidvattenskrafterna, men mindre eftersom fast material gör större mekaniskt motstånd.

Figuren i mitten nedan visar vad som händer i en godtycklig punkt A på havsytan. Eftersom avståndet MA' är större än MA kommer kraften i A vara större än kraften i A' (nedre triangeln). Vi får alltså i detta fall en resulterande kraft riktad uppåt till höger.

Motsvarande beräkning för hela klotet ger resultatet i den nedre figuren. De resulterande krafterna kommer att deformera klotet så att vi får en rotationsellipsoid med storaxeln riktad mot månen. Observera att de resulterande krafterna finns på den odeformerade jorden. När vattnet anpassat sig kommer den extra höjden på vattenpelaren att kompensera kraften och vi har jämvikt.

Vi har här bortsett från jordens rotation. Om man även tar hänsyn till denna och friktionen kommer ellipsoiden att vridas, se fråga 13056 .

Experiment med resonans

Ta en balja eller en spann och fyll i vatten till några centimeters djup. Skaka baljan fram och tillbaka med jämn rytm. Pröva med olika rytmer. Vid vissa skakningsrytmer blir det bara små vågeffekter. Vid andra rytmer blir vågorna bara större och större, så att det till slut skvalpar ut. Det fenomenet kallar vi resonans.

Diskussion av till synes olika förklaringar

En del förklaringar till tidvattenseffekten involverar centrifugalkraften, t.ex. The Cause of Tides (easy version) och OUR RESTLESS TIDES , medan andra som ovan inte gör det.

Anledningen till skillnaden är vilket koordinatsystem man föredrar. Ovan har vi föredragit jordens masscentrum. I detta har vi ingen acceleration (vi står förhoppningsvis stadigt på jordytan) och deformationen orsakas av skillnaden i gravitation i olika punkter på jorden.

Om vi i stället betraktar systemet jorden-månen från deras gemensamma masscentrum (som ligger c:a 1/4 jordradie under jordytan), så accelereras jorden hela tiden (roterar kring masscentret), och vi måste ta hänsyn till centrifugalkraften.

Observera är deformationen inte uppkommer bara vid rotationsrörelse, utan jorden skulle vara en ellipsoid även om den föll fritt mot månen, se Tidal_force för exempel på denna effekt.

Se även Tidvatten och länk 1 och 2.

Nyckelord: tidvatten [15]; centrifugalkraft [15];

1 https://www.grundskoleboken.se/wiki/Tidvatten
2 https://www.smhi.se/kunskapsbanken/oceanografi/tidvatten-1.321

Svar:
För att svara på din fråga så måste vi utreda vad en kraft är. Kroppar påverkar varandra, jorden attraherar till exempel en sten, stolen som Du sitter på trycker på Dig, magneten drar i ett järnstycke. Krafter används för att beskriva sådan mekanisk påverkan.

Då kommer vi till en filosofisk fråga: Finns krafter? Mitt svar är nog att krafter inte finns i naturen utan endast i vår beskrivning av naturen.

Nu till centrifugalkraften. Om Du åker karusell så kan vi beskriva Din rörelse på två sätt: Dels att Du rör Dig i en cirkel och dels att Du sitter still i karusellen. Om vi väljer det senare synsättet så måste vi införa en ny typ av krafter, så kallade tröghetskrafter. Centrifugalkraften är en sådan kraft.

Svaret på Din fråga är: Egentligen finns inga krafter utan vi måste själva införa dem i fysiken och vi kan även införa centrifugalkraften om vi så vill!
/GO

Nyckelord: centrifugalkraft [15];

Ämnesområde	BlandatElektricitet-MagnetismEnergiKraft-RörelseLjud-Ljus-VågorMateriens innersta-Atomer-KärnorPartiklarUniversum-Solen-PlaneternaVärme
Sök efter
Grundskolan eller gymnasiet?	FörskolaGrundskolaGymnasiumLärarutbildning
Nyckelord:	#ljus [63]*astronomi/astrofysik och rymdfart [2]*biologi [20]*fysikaliska definitioner [1]*fysiologi [13]*geologi [16]*idrottsfysik [42]*kemi [22]*meteorologi [20]*miljöpåverkan [14]*nöjesparksfysik [12]*vardagsfysik [64]*verktyg [15]3d-bilder [6]aberration [1]absoluta nollpunkten [9]acceleration [6]accelerator [7]addition av hastigheter [2]aerosol [4]akustik [6]alfasönderfall [7]annihilation [14]antimateria [16]arbete [24]Arkimedes princip [32]asteroid [10]astrobiologi [9]astrologi [5]atomradie [8]Avogadros tal [3]ballong [25]bandgenerator [3]barometerformeln [1]batteri [25]belysning [6]bernoullieffekten [6]betasönderfall [15]big bang [37]bildskärmar [4]bindningsenergi [23]blixt [18]blå himmel [12]bobåkning/störtlopp [4]Bohrs atommodell [9]Bose-Einstein-kondensat [6]brandvarnare [2]bränslecell [3]centrifugalkraft [15]centripetalkraft [11]comptonspridning [3]corioliskraft [7]dagens längd [3]daggpunkten [2]dagjämning [6]Darwins evolutionsteori [8]de Broglie våglängd [1]decibel [11]delton [2]diffraktion [4]diffusion [1]dimensionsanalys [7]dimkammare [2]dopplereffekt (ljud) [3]dopplereffekt (ljus) [3]drickande fågeln [1]dubbelspalt [4]duschdraperi [2]Einstein, Albert [1]eko [3]elasticitet [4]elastisk stöt [12]elektrisk krets [7]elektrisk ström, hastighet [4]elektrisk ström, skada [6]elektromagnetisk strålning [21]elektronskal [12]elektrostatik [4]elsäkerhet [18]energikällor [26]energilagringssystem [7]enkelspalt [1]entropi [7]EPR, Bell, Aspect [3]evighetsmaskin [14]exoplaneter [17]fallrörelse [31]faradaybur [10]fasdiagram [7]felberäkning [6]Fermats princip [1]ferromagnetism [9]fiberoptik [4]fission [15]fluorescens [6]flygplansvinge [8]flykthastighet [4]formel 1 [2]forskningskarriär [1]fossila bränslen [13]fotoelektrisk effekt [7]foton [6]friktion [53]friktionskoefficient [5]frågelådan [14]Fukushima [6]fusion [17]fysik [10]fysik, förståelse av [17]fysik, historia [1]fysik, nytta med [6]fysikalisk modell [12]färg/färgseende [39]färgkraften [8]Gaia [3]galax [28]gamma ray burst [2]gaslagen, allmänna [24]generator [1]genomskinlighet [18]genteknik [2]geodesi/gravimetri [2]geostationär satellit [8]gitter [5]g-krafter [18]glasögon [2]gluoner [7]glödlampa [23]gnistkammare [1]golfboll [15]GPS [3]gravitation [7]gravitationslins [5]gravitationsvågor [19]gravity assist [2]gregorianska kalendern [1]grundämnen, bildandet av [5]grundämnen, förekomst [4]gränshastighet [4]gunga [4]gyroskop [1]halofenomen [2]halogenlampa [3]halveringstid/sönderfallskonstant [5]harmonisk svängning [4]Heisenbergs obestämdhetsrelation [12]helikopter [5]higgspartikeln [10]Hiroshima/Nagasaki [4]hologram [5]HR-diagram [3]Huygens princip [3]hyperfinstruktur [1]hägring [4]händelsehorisont [4]hävstång [5]hörsel [10]Illustrerad Vetenskap [17]impedans [3]induktans [6]induktion [13]inertialsystem [6]inflation [7]infraljud [7]interferens [14]Internationella rymdstationen [6]iskristaller [5]istider [8]joniserande strålning [4]jordens atmosfär [12]jordens inre [14]jordens magnetfält [22]jordens rotation [22]kall fusion [8]kaos [3]kapillärkraft [12]kastparabel [10]Keplers lagar [14]Kirchhoffs strålningslag [4]klimat [11]knäppande aluminiumfolie [2]kokande vatten [17]kokpunkts/fryspunkts förändring [14]kol [3]kol-14 metoden [4]koldioxidcykeln [6]kollisionssäkerhet [1]komet [14]kosmisk bakgrundsstrålning [19]kosmisk strålning [5]kosmologi [33]kraft [12]kraftledning [7]kraftverkningar [9]kursplan [3]kvantmekanik [30]kvark [12]kvasar [4]kylning [7]kärndata [3]kärnenergi [19]kärnfysik [2]kärnkrafter [7]kärnkraftsavfall [11]kärnreaktion [5]kärnvapen [16]Lagrange-punkt [2]latitud/longitud [1]lins [11]liv i universum [9]livets uppkomst [1]ljud [11]ljud, interferens [7]ljud, resonans [19]ljudbang [3]ljudhastigheten [21]ljusbrytning [26]ljushastigheten [24]ljusreflektion [18]lorentztransformation [2]luftmotstånd [11]lufttryck [23]luminiscens [5]lutande plan [15]lysdiod [14]lysrör [10]lågenergilampa [13]längdkontraktion [6]magnetisk monopol [4]magnetism [52]magnetron [1]Mars [12]massa, trög/tung [4]massa-energi [1]massa-kraft [1]massbestämning [2]mass-luminositetsrelation [2]matematik i fysik [6]matematik, skriva [2]materia [6]Maxwells ekvationer [3]metabolism [3]metall, smältpunkt [3]meteorit [21]mikrovågsugn [25]Milankovitch cykler [3]mobiltelefon, strålning från [6]monstervåg [4]Monte Carlo-metoder [1]Mpemba-effekten [2]MRI [5]musikinstrument [19]månens bana [14]månens synbara storlek [1]månfärder [7]mörk energi [6]mörk materia [17]nanoteknik [6]Nationalencyklopedin [1]naturkonstant [7]naturlig radioaktivitet [3]nebulosa [13]NEO [10]neutrino [19]neutron [4]neutronstjärna [11]Newtons gravitationslag [12]Newtons rörelselagar [21]Newtons vagga [2]norrsken [7]nova [1]nyheter [11]Olbers paradox [2]orgelpipa [4]osmos [8]parallaxmetoden [4]parapsykologi [6]parbildning [7]Pascals lag [5]pauliprincipen [10]pendel, konisk [2]pendel, plan [9]PET [1]Plancks strålningslag [6]planet [17]planeters atmosfär [4]planeters form [3]plastfolie [1]polarisation [7]polaroidglasögon [3]potential/potentiell energi [30]prisma [1]projektarbete [1]pseudovetenskap [11]QED [7]radioaktiv datering [7]radioaktivitet, sönderfallskedja [7]radioaktivt sönderfall [38]radioteleskop [1]radon [4]raketekvationen [2]raketmotor [8]regn [1]regnbåge [6]relativistiskt massberoende [4]relativitetsteorin, allmänna [33]relativitetsteorin, speciella [45]religion [3]resistans [15]resistansförluster [2]resonans [5]richterskalan [2]ringklocka [5]rymddräkt [5]rymdfärder [23]rödförskjutning [7]röntgenrör [3]rörelseenergi [14]rörelsemängd [15]rörelsemängdsmoment [14]satellitbana [15]Saturnus´ ringar [6]schrödingerekvationen [4]Schrödingers katt [2]science fiction [6]segling [5]serie- och parallellkoppling [19]SETI [1]shareware [1]SI-enheter [6]skruvad boll [10]skymning [1]slumptal [1]SN 1987A [4]solaktivitet [2]solarkonstanten [6]solcell [7]solen [5]solen, avstånd till [1]solenergi [14]solens energiproduktion [9]solens utveckling [4]solförmörkelse [3]solsystemet [8]solsystemet, avstånd och rörelse [3]solsystemets bildande [12]specifik värmekapacitet [25]spegel [10]spektrum [11]standardmodellen [24]statisk elektricitet [12]stearinljuslåga [16]stjärna [4]stjärnhimlen [12]stjärnors utveckling [15]stroboskopeffekt [3]strålning, faror med [26]strålning, in-/ut- [6]strängteori [7]strömning [1]supernova [13]supertunga grundämnen [1]supraledning [7]svart hål [51]synvilla [6]sönderfallskonstant [5]teleskop [10]temperatur/temperaturskalor [17]temperaturstrålning [29]termodynamik [17]termometer [8]termos [3]Three Mile Island [3]tid [10]tidsdilatation [6]tidsekvation [4]tidvatten [15]tjerenkovstrålning [2]Tjernobyl [12]totalreflektion [9]transformator [6]transmutation av kärnavfall [2]trefas [3]trippelpunkt [2]tröghetsmoment [9]tsunami [5]tunneleffekt [3]TV [9]tvillingparadoxen [5]tyngdaccelerationen [16]tyngdlöshet [13]ultraljud [9]universums expansion [16]uppvärmning av bostäder [2]utvidgning [8]UV-ljus [13]vakuum [9]vatten/is [49]vattenkraft [7]vattenpump [2]vattenånga [2]Venus [11]verkningsgrad [26]vetenskaplig metod [18]Wikipedia [5]WIMPs [3]vindavkylning [4]vindenergi [12]Vintergatan [6]vridmoment [7]vulkanism [5]våg/partikelegenskaper [8]vågenergi [3]vågfunktion [2]värmemängd [3]värmepump/kylskåp [8]värmeöverföring/transport [46]väteatomen [2]vätskedroppsmodellen [5]växthuseffekten [36]ytspänning [18]årstider [4]ögat [18] (Enda villkor)
Definition:	(transmissions)mediumabsoluta nollpunktenabsorptionsspektraaccelerationackommodationackretionsskivaadiabatisk processaerodynamic heatingaerosolaggregationstillståndakustisk impedansallmänna gaslagenampereamperetimmeannihilationantigravitationantimateriaantropiska principenarbetearkimedes principasteroidasteroidbältetastigmatismastrobiologiastronomisk enhetatommassaatomnummeravogadros talbandspektrabatteribenhams snurrabergvärmebernoullis ekvationbetasönderfallbig bangbindningsenergibindningsenergibioluminiscensboltzmanns konstantbose–einstein-kondensatbrewstervinkelnbrownsk rörelsebrytningsindexbrännpunktbubbelkammarecarnotprocesscentrifugalkraftcentripetalkraftcirkumpolära stjärnorcitronbattericorioliskraftencurietemperaturendarwins evolutionsteoride broglie våglängdendecibeldeltonden kosmologiska principendensitetdielektrisk polarisationdielektriskt materialdiffus reflektiondiffusiondigitalkameradimensiondioptridiskret spektrumdispersiondopplereffektdotternukliddulong-petits lage=mc2ekliptikanekoekvivalensprincipenelasticitetelastisk energieldelektrisk dipolelektrisk laddningelektrisk spänningelektrisk strömelektriska fältstyrkanelektroluminiscenselektromagnetisk strålningelektroninfångningelektronskalelementarladdningenelementarpartiklaremissionsnebulosaemissionsspektraemsendoterm reaktionenergienergikällaenergiomvandlingenergipincipenenergipotentialentropi (makroskopisk definition)entropi (mikroskopisk definition)evighetsmaskinexciterade tillståndexoplanetexoterm reaktionextremofilerfallrörelsefaradays burfasdiagramfermats principferminivånferromagnetismfissionfjärde generationens reaktorfluidfluorescensflygplansvingeflykthastighetenfokalpunktfokusfosforescensfossila bränslenfotokromismfotomotståndfotonfotosfärenfotosyntesfouriers lagfraktalfranck-hertz försökfriktionfriktionskoefficientfritt fallfukushimafundamentala naturkrafternafusionfysikfysikaliska modellerfysiologifärgfärgblindhetfärgseendefönybara bränslenförnybara energikällorgaiagalaxgammastrålninggaskonstantengeneratorgeostationär satellitgeotermisk energiglobal uppvärmninggluonerglödlampagravitationgravitationengravitationskonstantengravitationsvågorgrundläggande fysikgrundtillståndetgrundtongrundämnegrå starrgränshastighetgula fläckenhalleffekthalogenlampahalveringstidhastighethawkingstrålningheisenbergs obestämdhetsrelationhertzsprung-russell diagramhiggspartikelnhookes laghornhinnanhubble ultra deep fieldhuygens principhydrostatiska paradoxenhägringhändelsehorisontenhästkrafthävstångicke-joniserande strålningideal gasimpedansinduktansinduktioninertialsysteminflationinfraljudinfraröd strålninginklinationinre konversioninre resistansinterferensinverterad populationisomerisospinnisoterm processisotoperjondriftjoniserande strålningjordfelsbrytarekalibreringkall fusionkalorikapacitanskapillärkraftenkastparabelkedjereaktionkemisk bindningkemisk bindningkemisk reaktionkemoluminiscenskeplers andra lagkeplers första lagkeplers tredje lagkilogramkirchhoffs lagkirchhoffs strålningslagkiselklassisk fysikklorofyllkokarreaktorkokpunktkolkornsmikrofonkometkomplementfärgkondensatorkonduktanskonservativ kraftkonserveringslagkontinuerligt spektrumkonvektionkoronankorrespondesprincipenkosmiska bakgrundsstrålningenkosmologikosmologiska rödskiftetkosmologiska standarmodellenkraftkristallkritisk densitetkritisk massakromosfärenkuiperbältetkundts rörkvantdatorkvantmekanikkvantmekanisk sammanflätningkvarkkvark-gluon plasmakvartskvasarkvasipartiklarkärnkrafterkärnreaktionkärnreaktorerkärnvapenlagrange-punkternalaserlenz lagleptonlila linjespektralivljudljusljusabsorptionljusbrytningljushastighetenljuskällorljusutbyteljusårlongitudinell våglorentzkraftenluftmotståndluminiscenslutande planlysdiodlysrörlågenergilampalägesenergilängdkontraktionmachomagnetismmagnuseffektenmarkradarmarkvärmemaskhålmassamasscentrummassdefektmassenhetmassexcessmasstalmateriamaxwell–boltzmannfördelningenmaxwells ekvationermedelvärdetmegaton tntmeissnereffektenmekanikens gyllene regelmerkurius periheliumprecessionmetafysikmetallbindningmetalldetektormetallicitetmeteormeteoritmeteoroidmilankovitch cyklermodern fysikmodernuklidmolmolekylmultiversummymetallmånemätfelmörk energimörk materiamörk nebulosamössbauer-effektennanometertekniknanopartikelnanotekniknationalencyklopedinnaturvetenskapnavigeringneoneutrinoneutrinooscillationerneutroninducerad fissionneutronstjärnanewtonnewtonringarnewtons andra lagnewtons avsvalningslagnewtons första lag (tröghetslagen)newtons gravitationslagnewtons tredje lagnobelpris i fysik 1925nobelpris i fysik 1993nobelpris i fysik 2015nobelpris i fysik 2017nobelpris i fysik 2020normalkraftennorrskennuklidnuklidkartanutida fysiknärsynthetockhams rakknivohms lagoorts kometmolnoregelbunden galaxosmosparapsykologiparbildningpascals princippauliprincipenperiodiska systemetplanck timeplancks strålningslagplanetplanetarisk nebulosaplasmaplasmaplasmaplasticitetpn-övergångpolarisationpolspänningpolär jetstrålepotentialproton-protonkedjanpseudovetenskapqcdqedradiative forcingradioaktivitetradioluminiscensraketekvationenrayleigh-spridningreaktansreflektionreflektionsnebulosarefraktionregnbågerelativ luftfuktighetrelativistisk energirelativistisk jetresistansresistivitetresistivitetresonansroche-gränsenrullmotståndrussells tekannarödförskjutningrörelseenergirörelsemängdrörelsemängdsmomentschwarzschildradiensekulär jämviktsekundsfärisk aberrationsi-enheternasingularitetsi-prefixsi-systemetsjälvinduktansskalärproduktskottsekundslipstreamslumpvisa mätfelsmältvärmesnells lagsolarkonstantensolcellersolenergisolens centrumsolförmörkelsesolkraftverksolvindsolvärmespallationspecifik värmekapacitetspektroskopispektrumspinnspontan fissionstandardavvikelsenstandardmodellenstatisk elektricitetstefan–boltzmanns lagstimulerad emissionstjärnastjärnbildstorhetstrålningstrålningstråloptiksträngteorinstående vågstämgaffelsublimationsupermassiva svarta hålsupernovasupertungt grundämnesuprafluiditetsupraledningsvart hålsvartkroppsvänghjulsystematiska mätfelsåpbubblasäkringsönderfallskedjasönderfallskonstantentemperaturtemperaturspektrumtemperaturstrålningtensortermodynamiktermodynamikens andra huvudsatstermodynamikens första huvudsatsthree mile islandtidtidens riktningtidsdilatationtidsekvationentidvattentidvattenkraftertillämpad fysiktjerenkovstrålningtjernobyltotalreflektiontransformatortransistortransparenstriboelektrisk effekttrippelpunktentrycktryckvattenreaktortröga massantröghettröghetsmomenttunga massantvillingparadoxentyngdtyngdaccelerationtyngdlöshettyngdpunktentyp ii supernovaufoultraljudultraviolett strålningultraviolettkatastrofenunderkylninguniversums åldervakuumvakuumfluktuationervakuumpolarisationvalenselektronvattenburen värmevattenkraftvattenkraftvattenångavektorerverkningsgradvetenskaplig metodwiens förskjutningslagwikipediaviktwimpvindkraftvintergatanvintergatanvirtuell bildvirtuell bildvit dvärgvoltvridmomentv-t diagramvåglängdenvåg-partikeldualitetvågtalvärmeledningvärmemängdvärmepumpvärmepumpvärmeöverföringvätebindningvätelika jonervätskedroppsmodellenväxthuseffektenytenergiångbildningsvärmeångtryckårstidernaåskaädelgasädelgaserögats linsöratöversynthetövertoner (Enda villkor)

---

Om du inte hittar svaret i databasen eller i

Sök i svenska Wikipedia:

Sök i Nationalencyklopedin

   

Sök med Google

   

- fråga gärna här.