Svar:
Du har förstått rätt.

Vi har tre krafter att ta hänsyn till

1 Gravitationskraften som vid jordytan är F=mg och är riktad nedåt.

2 Eventuell bromsande kraft t.ex. från jordytan eller luftmotstånd.

3 Kraften från en eventuell raketmotor.

Om kraften 2 och 3 saknas befinner du dig i fritt fall och du accelererar fullt ut. Du och din rymdkapsel accelererar med samma belopp och riktning så du har en känsla av tyngdlöshet.

Om du ger kapseln en ytterligare acceleration med en raketmotor så påverkas kapseln av summan (observera att acceleration är en vektor som har både värde och riktning, se fråga 20617 ) av de två krafterna. Om raketmotorn är riktad bakåt kommer accelerationen framåt att öka. Du kommer att känna av kraften från raketmotorn, så du bör sitta fastspänd i din stol.

Se fråga 282 för mer om tyngdlöshet.
/Peter E

Nyckelord: tyngdaccelerationen [16]; tyngdlöshet [13];

Ursprunglig fråga:
Hej,

Jag har försök att lösa denna uppgift men jag lyckas inte få fram svaret och undrar om du kan hjälpa till. Lös ut g ur formeln T = 2π√I/Mgh , där I är pendelns tröghetsmoment med avseende på axeln, M är massan i kg och h avståndet i meter från axeln till pendelns tyngdpunkt. SI-enhet för tröghetsmoment är kg*m2.
/Alisya L, Stockholm

Svar:
Alisya!

Såvitt jag förstår är du ute efter att bestämma tyngdaccelerationen g genom att mäta svängningstiden för en plan pendel.

Tyngdacceleration är inom klassisk mekanik den acceleration som är resultatet av kombinationen av gravitationsaccelerationen och den centrifugalacceleration som härrör från en kropps rotation, till exempel jordens rotation. Tyngdaccelerationen på jordytan, också kallad jordaccelerationen, varierar med latitud, mellan cirka 9,78 m/s² vid ekvatorn och 9,83 m/s² vid polerna. (Tyngdacceleration )

Den formel du ger är korrekt men för en fysikalisk pendel. Problemet med denna är att uttrycket för perioden innehåller flera parametrar som är svåra att uppskatta, speciellt tröghetsmomentet I. Se Pendel#Fysikalisk_pendel .

Man kan i stället använda sig av en enklare modell, en s.k. Matematisk pendel, se Pendel#Matematisk_pendel . Svängningstiden för en sådan härleds i fråga 14065 :

T = 2*p*√(l/g)

Som du ser innehåller formeln T, l och g. Genom att mäta l och motsvarande T kan du alltså räkna ut ett värde på g.

För att få ett tillförlitligt svar bör du mäta tiden för flera pendelcykler (l), t.ex. 10-20 stycken. Du kan även göra mätningen med flera pendellängder (l) och ta medelvärdet på resultaten.

Se även fråga 4287 .
/Peter E

Nyckelord: pendel, plan [9]; tyngdaccelerationen [16];

Svar:
Använd uttrycket

s = at²/2

a = (ditt värde på g) = (2*4.2)/(0.99)² = 8.57 m/s²

Det är betydligt mindre än det korrekta 9.82 m/s². Detta kan bero på att luftmotståndet försummas.

Se även fråga 4287 och Fritt_fall .
/Peter E

Nyckelord: tyngdaccelerationen [16]; fallrörelse [31];

Svar:
Med formeln i fråga 4287 kan du få fram g för Hallsbergs latitud (länk 1 ger 59°05'N).

Du kan korrigera för höjden över havet med formeln i Gravity_of_Earth#Altitude .

För avvikelser på grund av berggrundsförhållanden måste man använda mätningar. Dessa lär finnas hos Lantmäteriet, se länk 2. Jag tror emellertid att korrektionerna är ganska små.
/Peter E

Nyckelord: tyngdaccelerationen [16];

1 http://www.mapsofworld.com/lat_long/sweden-lat-long.html
2 http://www.lantmateriet.se/sv/Kartor-och-geografisk-information/GPS-och-geodetisk-matning/Referenssystem/Tyngdkraftssystem/Tyngdkraften/

Ursprunglig fråga:
Eriks tyngd på månen är 100 Newton. Hur mycket väger Erik?
/Abdulla K, Klaraprivata, Spånga

Svar:
Först måste du räkna ut tyngdaccelerationen på månen. Enligt fråga 16455 ges månens tyngdacceleration av

g_månen = (M G)/R²

Månens massa M och radie R finns på länk 1. Gravitationskonstanten G är 6.67384×10^-11 m³ kg^-1 s^-2.

g_månen = (0.07342*10²⁴ 6.67384*10^-11)/(1737.1*10³)² = 1.62 m/s²

Förhållandet

g_jorden/g_månen = 9.81/1.62 = 6.06

Eriks tyngd på jorden

6.06*100 = 606 N

och hans vikt (massa, se fråga 16048 ) är

606/9.81 = 61.8 kg

oberoende var han befinner sig.
/Peter E

Nyckelord: tyngdaccelerationen [16];

1 http://nssdc.gsfc.nasa.gov/planetary/factsheet/moonfact.html

Ursprunglig fråga:
Om jag hade kastat ett föremål rakt ut, hur hårt skulle jag minst behöva kasta för att det aldrig skulle landa om vi bortser från eventuella bromsande krafter?
/Gent S, göteborg, falunskolan

Svar:
Det finns flera sätt att härleda den erforderliga hastigheten för en satellitbana nära jordytan. Låt oss börja med den mest direkta metoden, se figuren nedan. Om hastigheten för en låg cirkelbana är v så är sträckan mot horisonten på en sekund lika med v*1 m. Under en sekund faller föremålet med accelerationen g sträckan

gt²/2 = 9.81/2 m

Jordens radie är r=6.37*10⁶ m (Planetary Fact Sheets ). I figuren har vi två likformiga trianglar (observera att a är mycket liten så jordens krökning och skillnaden mellan katet och hypotenusa är försumbar):

(9.81/2)/v = (v/2)/r

v² = 9.81*r = 9.81*6.37*10⁶ = 62.5*10⁶

v = 7.91*10³ m/s = 7.91 km/s

Man kan även härleda hastigheten från Keplers tredje lag, se fråga 12644

P² = 4p²*a³/(G*M)

För en cirkelbana är halva storaxeln a lika med radien r. Om man tar G från fråga 12644 och M från Planetary Fact Sheets , får man

P² = 4p²*(6.37*10⁶)³/(6.673*10^-11*5.97*10²⁴) = 25.6*10⁶

och

P = 5050 s = 84.2 minuter (omloppstid)

Banhastigheten v blir

v = s/t = 2p*r/5050 = 7.92*10³ m/s = 7.92 km/s

i god överensstämmelse med värdet ovan.

Länk 1 har en lättillgänglig och trevlig animering av problemet. Länk 2 förklarar relativt ingående. Se även Orbit#Understanding_orbits och fråga 463 .

Se fråga 19564 för en alternativ lösning.

Nyckelord: Keplers lagar [14]; tyngdaccelerationen [16]; satellitbana [15];

1 http://spaceplace.nasa.gov/how-orbits-work/
2 http://www.physicsclassroom.com/mmedia/vectors/sat.cfm

Ursprunglig fråga:
Varför väger man olika på gas-planeterna? Tacksam för svar.
/Hanol B, Råbyskolan, Bro

Svar:
Hur mycket du väger beror på tyngdaccelerationen g (tyngdkraften blir m*g där m är din massa). Tyngdaccelerationen ges enligt fråga 15114 av

g = (M G)/R²

där G är Newtons universella gravitationskonstant, M är planetens massa och R är dess radie. Tyngdaccelerationen ökar alltså med ökande massa M och minskar med ökande radie R. Massor och radier för planeter kan du hitta i Planetary Fact Sheets .

Låt oss räkna ut g på "ytan" av Jupiter:

Jupiters massa M: 1898*10²⁴ kg
Jupiters radie R: 70*10⁶ m
Gravitationskonstanten G: 6.67*10^-11 m³/ (kg s²)

g(Jupiter) = (M G)/R² = 26 m/s²

alltså c:a 2.5 gånger jordens.

Se länk 1 för tyngaccelerationen hos fler objekt.

Vi kan skriva om ovanstående uttryck som

g = R*G*M/R³.

Eftersom medeldensiteten r är proportionell mot M/R³ blir g proportionellt mot

R*G*r

Större radie ger alltså större g för konstant medeldensitet.

Sedan är det en annan sak att allt detta är ganska teoretiskt för en gas-planet. Eftersom det inte finns någon fast yta har du inget att stå på, så du befinner dig i fritt fall (bortsett från luftmotståndet).
/Peter E

Nyckelord: tyngdaccelerationen [16];

1 http://settlement.arc.nasa.gov/teacher/lessons/bryan/microgravity/gravback.html

Svar:
Hanna! Eftersom jorden roterar med en konstant vinkelhastighet märker du egentligen inget direkt. Det enda är att du ser solen, månen, planeter och stjärnor röra sig över himlen. Dessutom påverkas t.ex. vindar delvis av jordens rotation.

Eftersom vinkelhastigheten är konstant, så är hastigheten beroende av latituden. Befinner du dig nära polerna så är hastigheten låg, befinner du dig nära ekvatorn så är hastigheten hög (c:a 0.5 km/sekund). Detta medför en liten ändring i värdet på tyngdaccelerationen och att lodlinjen avviker lite (0.1 grader) från en linje genom jordens centrum, se fråga 14923 nedan.
/Peter E

Se även fråga 14923

Nyckelord: tyngdaccelerationen [16];

Svar:
Gravitationskraften på en massa m är

F = ma = (mM G)/r²

där M är jordens massa, G gravitationskonstanten, R jordradien och r är avståndet från centrum.

Tyngdaccelerationen g ges då av

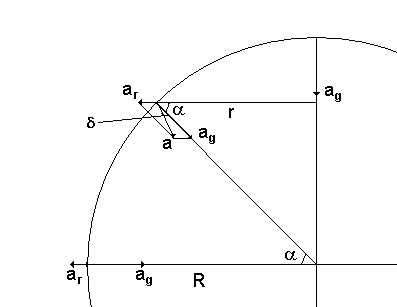
g = a = (M G)/R² = (5.98 10²⁴ 6.673 10^-11)/(6.38 10⁶)² = 9.80 m/s²

Tyngdaccelerationen på avståndet r från jordens centrum (r>R) blir:

g(r) = g/(r/R)²

Om vi sätter g(r) = g/2 får vi

(r/R)² = 2

dvs

r = sqrt(2)*R = 1.414R

Avståndet över marken blir då

(1.414 - 1)R = 0.414R = 0.414*6.38*10⁶ = 2640000 m = 2640 km.
/Peter E

Nyckelord: tyngdaccelerationen [16];

Ursprunglig fråga:
Om man står på marken bör man se till att hålla sin egen tyngdpunkt på en linje genom jordens tyngdpunkt och sina egna fötter, annars trillar man ikull. Men, hur muycket påverkar den centrifugalkraft som jordrotationen ger upphov till detta? Inte alls om man står på ekvatorn eller nord(syd)polen. Men i Skåne! Hur många grader (eller fraktioner av en grad) måste man luta sig "inåt" (dvs mot norr) för att inte falla ikull pga centrifugalkraften?
/Jon L

Svar:
Jon! Det är en helt omärkbar effekt och det är knappast någon risk att man trillar, men låt oss som en övning räkna ut hur stor effekten är. Vi antar att jorden är klotformad och homogen med radien R. Den enda effekt vi tar hänsyn till är jordens rotation, vi bortser alltså från tillplattningen. Vi inför några beteckningar (se figuren):

a_g = 9.822 m/s² tyngdaccelerationen från jordens dragningskraft, se länk 1
a_r accelerationen pga jordens rotation
a den resulterande tyngdaccelerationen
R = 6.37*10⁶ m jordradien
a latituden
w = 2p/(24*60*60) = 72.7*10^-6 s^-1 vinkelhastigheten för jordens rotation

Vid polerna och ekvatorn är det ingen avvikelse i vinkel mellan a och a_g (precis som du säger) medan det för medelhöga latituder är en avvikelse så att det är en liten "uppförsbacke" när man går norrut. Om du så vill kan du förstå detta som att "centrifugalkraften" försöker hindra dig att gå närmare rotationsaxeln.

Låt oss börja med att se vad som händer vid ekvatorn. Rotationshastigheten ges av

v = R*w = 6.37*10⁶*72.7*10^-6 = 463 m/s

Accelerationen pga rotationen blir

a_r = v²/R = R*w² = 6.37*10⁶*(72.7*10^-6)² = 0.0337 m/s²

Tyngdaccelerationen vid ekvatorn blir alltså

a_g - a_r = 9.822 - 0.0337 = 9.788 m/s²

Accelerationen pga rotationen vid latituden a blir

a_g = r*w² = R*cosa*w²

Tillämpning av cosinuseoremet på triangeln a_g, a_r, a ger

a² = a_g² + a_r² -2a_ga_rcos(a)

Den andra termen i högra ledet är mycket liten så vi kan försumma den. Vi får då

a = a_g(1 - 2Rw²cos²a/a_g)^1/2 = a_g(1 - Rw²cos²a/a_g) = a_g(1 - 0.0337*cos²a/9.822)

a = a_g(1 - 0.00343*cos²a)

Lodlinjens avvikelse från riktningen mot jordens medelpunkt d kan beräknas genom att vi tillämpar sinusteoremet på triangeln:

sind/a_r = sina/a

sind = a_r*sina/a = Rw²*cosa*sina/a = Rw²*sin2a/2a

Från detta uttryck kan vi se att avvikelsen är maximal för a=45^o och noll för a=0^o och a=90^o.

Eftersom a är approximativt lika med a_g och eftersom vinkeln är liten (sind = d) får vi

d = Rw²*sin2a/2a_g = 0.0337*sin2a/(2*9.822) = 0.00172*sin2a

d i grader blir

d = 180*0.00172*sin2a/p = 0.0985*sin2a grader

Från detta kan vi se att lodlinjens maximala avvikelse (vid latituden 45^o) är c:a 0.1^o.

Nyckelord: tyngdaccelerationen [16]; centrifugalkraft [15]; jordens rotation [22];

1 http://en.wikipedia.org/wiki/Acceleration_due_to_gravity

Svar:
Hej Ion! Tack, för den positiva recensionen - smicker är alltid en bra taktik !

De du frågar om är en del av geodesi, ett ämne som jag tyvärr inte vet särskilt mycket om. Till en stor del baseras emellertid geodesin på enkla fysikaliska principer, så lite skall jag väl kunna säga. Börja med att läsa de utmärkta artiklarna om geodesi, gravimetri och gravimeter i Nationalencyklopedin .

Geoforum (länk 1) definierar geodesi så här:

Geodesin är en av de äldsta naturvetenskaperna och sammankopplades länge med astronomi och geometri. Den naturvetenskapliga geodesin studerar jordens form, tyngdkraftsfält och dess dynamiska förändringar. En av geodesins viktigaste uppgifter är uppbyggande och underhållande av nationella och/eller globala koordinatsystem, som är av stor betydelse för all geografisk information. Vidare utvecklas avancerade geodetiska mätningstekniker för noggrann positionering och navigering med hjälp av moderna satellittekniker (t.ex. GPS – Global Positioning System).

Gravimetrar är instrument som kan mäta tyngdaccelerationen g med en precision på bättre än 1 del på 10⁹. De baseras på pendel, fjäder, svävande supraledande kula, fritt fall mm. För mer globala mätningar använder man sig av speciella satelliter i relativt låga banor. För detaljer se Geodesy and Gravity , som är en utmärkt och lättförståelig framställning av geodesi, framför allt mätmetoder och instrument.

Tillämpningar är, förutom att mäta upp och förstå jorden så bra som möjligt, t.ex. malmprospektering.
/Peter E

Nyckelord: geodesi/gravimetri [2]; tyngdaccelerationen [16];

1 http://www.geoforum.se

Om det är det, hur kan då Newton ha ett konstant förhållande gentemot en massas vikt i kg (c:a 9,8), då en massas vikt i kg varierar beroende på hur stark gravitationskraft massan utsätts för? T.ex. väger en människa olika mycket i kg beroende på vilken planet hon befinner sig på, hur kan hon då alltid ha ett konstant Newton-värde?
/Pontus X, Skärholmen, Stockholm

Svar:
Pontus! Om jag förstår dig rätt så undrar du varför det man kallar tröga massan m₁ (mängd materia) är lika med den tunga massan m₂ (hur massan påverkas av ett gravitationsfält).

Den tröga massan definieras av Newtons andra lag:

F = m₁ a

Den tunga massan definieras av Newtons gravitationslag:

F = Gm₂ M/r²

där gravitationskonstanten G är

G = 6.673 10^-11 m³s^-2kg^-1

Vi får accelerationen i ett tyngdkraftsfält (attraherande massan M och avståndet från massan r) genom att sätta kraften i tröghetslagen lika med gravitationskraften. Vi får

a = F/m₁ = (Gm₂ M/r²)/m₁

Om den tröga massan är lika med den tunga massan kan massorna elimineras och vi får

a = GM/r²

Accelerationen och därmed fallhastigheten är alltså oberoende av massan på den fallande kroppen!

Tyngdaccelerationen g vid jordytan blir

g = GM/R² = 6.673*10^-11*5.9736*10²⁴/(6.371*10⁶)² = 9.82 m/s²

där M är massan och R radien.

Hur kan vi förstå det faktum att den tröga massan och den tunga massan är lika? Jo, det är en naturlig följd av Einsteins allmänna relativitetsteori. Denna säger att gravitation är ekvivalent ("samma som") acceleration. Låt oss anta att vi har ett gravitationsfält som ger tyngdaccelerationen g (nedåt). Detta är då ekvivalent med en hiss som har accelerationen g (uppåt). Vad händer om du släpper en lätt kula och en tung kula mitt i hissen? I förhållande till hissen (som ju accelererar uppåt) rör sig kulorna hela tiden med samma hastighet (eftersom de inte påverkas av någon kraft). Eftersom vi sade att acceleration och tyngdkraft är ekvivalenta, faller alltså alla kroppar med samma hastighet oberoende av deras massa. Man kan säga att Einstein i förhållande till Newton bytte ut en ekvivalensprincip (trög massa=tung massa) mot en annan (tyngdkraft=acceleration).

Från Newtons gravitationslag kan man härleda att planeter och satelliter rör sig i elliptiska banor, se Elliptic_orbit . I själva verket kan man härleda alla tre Keplers lagar, se fråga 12644 .

Se vidare Mass och länk 1.
/Peter E

Se även fråga 12833 och fråga 13930

Nyckelord: Newtons gravitationslag [12]; massa, trög/tung [4]; tyngdaccelerationen [16];

1 http://einstein.stanford.edu/STEP/

Ursprunglig fråga:
Hur kan man beräkna massan för någon planet i vårt solsystem. För att beräkna massan för t.ex. Mars måste man ju känna till banhastigheten och avståndet till solen. men även solens massa måste ju vara känd, samt den gemensamma tyngdpunkten. Dom två första variablerna kan man säkert mäta sig till. Men hur gör man sedan?
/Lars B, Pauli, Malmö

Svar:
Låt oss först skissa bakgrunden. Från Tycho Brahes mycket exakta mätningar av planeten Mars' rörelse kunde Johannes Kepler få fram tre lagar för planeternas rörelser. Isaac Newton kunde senare förklara dessa rörelser med hjälp av en lag, gravitationslagen, och nyutvecklad matematik (differentialkalkyl).

Keplers första lag: Planetbanorna är ellipser med solen i den ena brännpunkten. (Se nedanstående figur.)

Keplers andra lag: Varje planet rör sig längs sin elliptiska bana med en sådan hastighet att en linje från planeten till solen ("radius vector") alltid sveper över en lika stor area på samma tid. (Se nedanstående figur.) Planeten rör sig alltså snabbare när den är nära solen än när den är längre ifrån.

Från sin gravitationslag kunde Newton härleda följande variant av Keplers tredje lag:

P är (sideriska) omloppstiden
a är halva storaxeln av banan
G är gravitationskonstanten
m₁ och m₂ är objektens massor

Gravitationskonstanten (Gravitational_constant ) bestämdes först av Henry Cavendish år 1798 med hjälp av tunga metallkulor och en torsionsvåg. Det aktuella värdet är

G = 6.673 10^-11 m³s^-2kg^-1

Eftersom gravitationskonstanten är svår att mäta är den en av de sämst kända naturkonstanterna.

Om vi sätter in värdet på G och förenklar lite får vi

(m₁+m₂) = (4*p²/G) a³/P² = 5.916 10¹¹ a³/P²

Detta uttryck kan tillämpas på vilket system av två objekt som helst, till exempel Mars och Mars' månar Phobos och Deimos eller t.o.m på ett svart hål i vintergatans centrum (se fråga 6228). Låt oss först tillämpa det på systemet jorden-månen:

(m₁+m₂) = 5.916 10¹¹ (384400000)³/(27.32*24*60*60)² = 6.03 10²⁴ kg.

Observera att vi måste använda SI enheter genomgående, dvs meter och sekunder. Från läget av jorden-månens gemensamma tyngdpunkt kan man bestämma m₁/m₂ till 81.3, så jordens massa blir 5.96 10²⁴ kg.

Tillämpat på systemet jorden-solen får vi

(m₁+m₂) = 5.916 10¹¹ (149600000000)³/(365.24*24*60*60)² = 1.99 10³⁰ kg.

Eftersom jordens massa kan försummas blir detta solens massa.

För planeter som saknar månar får man mäta deras påverkan av andra planeter. På senare tid har man ju skickat rymdsonder till många planeter, och då kan man bestämma planetens massa från sondens acceleration i närheten av planeten.

Observera att vi även kan bestämma jordens massa med hjälp av tyngdaccererationen 9.81 m/s² och Newtons gravitationslag:

F = ma = (mM G)/r² dvs

M = a r²/G = 9.81 (6.38 10⁶)²/(6.673 10^-11) = 5.98 10²⁴ kg.

Det var denna överensstämmelse som övertygade Newton (och andra) att det var samma kraft som påverkar varje massa på jorden (äpplet ) som den kraft som styr solsystemet.

Se även: Kepler's_laws_of_planetary_motion (avancerad), Johannes Kepler: The Laws of Planetary Motion (lite lättare) och Newton's Law of Gravity .

Formelsamling i fysik är en lättillgänglig sammanställning av fysikaliska formler och konstanter. Fysikalisk_konstant och den engelska versionen Physical_constant ger värden på fysikaliska konstanter.

Se även fråga 6228 och fråga 7808

Nyckelord: massbestämning [2]; Keplers lagar [14]; Newtons gravitationslag [12]; tyngdaccelerationen [16]; fallrörelse [31]; *verktyg [15];

Ursprunglig fråga:
Hur varierar Jordens gravitation om man gräver sig under ytan? Jordens gravitation 100 mil ovanför jordens yta är lätt att räkna ur, men hur stor är jordens gravitation 100 mil under jordens yta?
/Lars B, Fysiska institutionen Lund, Trelleborg

Svar:
Gravitationen (av latin gravis = tung) eller tyngdkraften är en av universums fyra fundamentala krafter, se fråga 3716 . Det är den attraherande kraft som massor utsätter varandra för, och ger upphov till det som vi kallar massans tyngd.

Gravitationskraften på massan m utanför ett klot med massan M ges av F=GmM/r², där r är avståndet till masscentrum. Gravitationen innanför klotets yta beror av massfördelningen, eftersom endast den del av klotets massa som ligger innanför r ger bidrag till attraktionen. Om jordens densitet är konstant (vilket den definitivt inte är), så ges massan innanför r av M'=Mr³/R³, där R är jordradien. Gravitationskraften under jordytan (r mindre än R) blir alltså: F=GmMr/R³.

Gravitationskraften vid jordens medelpunkt (r=0) blir alltså 0. Om man kunde borra ett hål rakt genom jorden (omöjligt eftersom det är mycket varmt i jordens centrum och materien är flytande) skulle man kunna falla rakt igenom jorden och komma ut (vända vid jordytan) på andra sidan - bortsett från luftmotståndet. Om vi bromsar fallet skulle vi kunna stanna i centrum och sväva i ett tyngdlöst tillstånd.

Figuren nedan visar den uppmätta densiteten i jordens inre (från seismiska vågor, se Structure_of_the_Earth ) och den beräknade tyngdaccelerationen. För de inre delarna kan man se att tyngdaccelerationen är approximativt proportionell mot r, medan den för de yttre delarna är närmast konstant.

Se även fråga 19792 .

Nyckelord: tyngdaccelerationen [16]; jordens inre [14]; fallrörelse [31];

1 https://www.physicscentral.com/explore/poster-earth.cfm
2 https://www.youtube.com/watch?v=urQCmMiHKQk

Svar:
Gravitationskonstanten är en generell konstant, som är lika i hela universum (så vitt vi vet).

Vad du säkert syftar på är tyngdaccelerationen, som varierar något beroende på var man är på jorden. Det beror på:

1. Jorden är tillplattad.

2. Centrifugalkraften på grund av jordrotationen.

3. Tidvattenfenomen orsakade av sol och måne.

4. Lokala variationer på grund av geologiska förhållanden.

En formel som tar hänsyn till de två första punkterna (Tyngdacceleration ) är:

g = g_o * ( 1 + 0.0052884 * sin²(b) - 0.0000059 * sin²(2b))

g_o = 9.78049 m/s²

b = latituden.

För Västervik får man då 9.81764 m/s².

Direkt uppmätta värden kan man få hos Sveriges geologiska undersökning, SGU , men då får man betala för det.
/KS/lpe

Nyckelord: tyngdaccelerationen [16];

Ämnesområde	BlandatElektricitet-MagnetismEnergiKraft-RörelseLjud-Ljus-VågorMateriens innersta-Atomer-KärnorPartiklarUniversum-Solen-PlaneternaVärme
Sök efter
Grundskolan eller gymnasiet?	FörskolaGrundskolaGymnasiumLärarutbildning
Nyckelord:	#ljus [63]*astronomi/astrofysik och rymdfart [2]*biologi [20]*fysikaliska definitioner [1]*fysiologi [13]*geologi [16]*idrottsfysik [42]*kemi [22]*meteorologi [20]*miljöpåverkan [14]*nöjesparksfysik [12]*vardagsfysik [64]*verktyg [15]3d-bilder [6]aberration [1]absoluta nollpunkten [9]acceleration [6]accelerator [7]addition av hastigheter [2]aerosol [4]akustik [6]alfasönderfall [7]annihilation [14]antimateria [16]arbete [24]Arkimedes princip [32]asteroid [10]astrobiologi [9]astrologi [5]atomradie [8]Avogadros tal [3]ballong [25]bandgenerator [3]barometerformeln [1]batteri [25]belysning [6]bernoullieffekten [6]betasönderfall [15]big bang [37]bildskärmar [4]bindningsenergi [23]blixt [18]blå himmel [12]bobåkning/störtlopp [4]Bohrs atommodell [9]Bose-Einstein-kondensat [6]brandvarnare [2]bränslecell [3]centrifugalkraft [15]centripetalkraft [11]comptonspridning [3]corioliskraft [7]dagens längd [3]daggpunkten [2]dagjämning [6]Darwins evolutionsteori [8]de Broglie våglängd [1]decibel [11]delton [2]diffraktion [4]diffusion [1]dimensionsanalys [7]dimkammare [2]dopplereffekt (ljud) [3]dopplereffekt (ljus) [3]drickande fågeln [1]dubbelspalt [4]duschdraperi [2]Einstein, Albert [1]eko [3]elasticitet [4]elastisk stöt [12]elektrisk krets [7]elektrisk ström, hastighet [4]elektrisk ström, skada [6]elektromagnetisk strålning [21]elektronskal [12]elektrostatik [4]elsäkerhet [18]energikällor [26]energilagringssystem [7]enkelspalt [1]entropi [7]EPR, Bell, Aspect [3]evighetsmaskin [14]exoplaneter [17]fallrörelse [31]faradaybur [10]fasdiagram [7]felberäkning [6]Fermats princip [1]ferromagnetism [9]fiberoptik [4]fission [15]fluorescens [6]flygplansvinge [8]flykthastighet [4]formel 1 [2]forskningskarriär [1]fossila bränslen [13]fotoelektrisk effekt [7]foton [6]friktion [53]friktionskoefficient [5]frågelådan [14]Fukushima [6]fusion [17]fysik [10]fysik, förståelse av [17]fysik, historia [1]fysik, nytta med [6]fysikalisk modell [12]färg/färgseende [39]färgkraften [8]Gaia [3]galax [28]gamma ray burst [2]gaslagen, allmänna [24]generator [1]genomskinlighet [18]genteknik [2]geodesi/gravimetri [2]geostationär satellit [8]gitter [5]g-krafter [18]glasögon [2]gluoner [7]glödlampa [23]gnistkammare [1]golfboll [15]GPS [3]gravitation [7]gravitationslins [5]gravitationsvågor [19]gravity assist [2]gregorianska kalendern [1]grundämnen, bildandet av [5]grundämnen, förekomst [4]gränshastighet [4]gunga [4]gyroskop [1]halofenomen [2]halogenlampa [3]halveringstid/sönderfallskonstant [5]harmonisk svängning [4]Heisenbergs obestämdhetsrelation [12]helikopter [5]higgspartikeln [10]Hiroshima/Nagasaki [4]hologram [5]HR-diagram [3]Huygens princip [3]hyperfinstruktur [1]hägring [4]händelsehorisont [4]hävstång [5]hörsel [10]Illustrerad Vetenskap [17]impedans [3]induktans [6]induktion [13]inertialsystem [6]inflation [7]infraljud [7]interferens [14]Internationella rymdstationen [6]iskristaller [5]istider [8]joniserande strålning [4]jordens atmosfär [12]jordens inre [14]jordens magnetfält [22]jordens rotation [22]kall fusion [8]kaos [3]kapillärkraft [12]kastparabel [10]Keplers lagar [14]Kirchhoffs strålningslag [4]klimat [11]knäppande aluminiumfolie [2]kokande vatten [17]kokpunkts/fryspunkts förändring [14]kol [3]kol-14 metoden [4]koldioxidcykeln [6]kollisionssäkerhet [1]komet [14]kosmisk bakgrundsstrålning [19]kosmisk strålning [5]kosmologi [33]kraft [12]kraftledning [7]kraftverkningar [9]kursplan [3]kvantmekanik [30]kvark [12]kvasar [4]kylning [7]kärndata [3]kärnenergi [19]kärnfysik [2]kärnkrafter [7]kärnkraftsavfall [11]kärnreaktion [5]kärnvapen [16]Lagrange-punkt [2]latitud/longitud [1]lins [11]liv i universum [9]livets uppkomst [1]ljud [11]ljud, interferens [7]ljud, resonans [19]ljudbang [3]ljudhastigheten [21]ljusbrytning [26]ljushastigheten [24]ljusreflektion [18]lorentztransformation [2]luftmotstånd [11]lufttryck [23]luminiscens [5]lutande plan [15]lysdiod [14]lysrör [10]lågenergilampa [13]längdkontraktion [6]magnetisk monopol [4]magnetism [52]magnetron [1]Mars [12]massa, trög/tung [4]massa-energi [1]massa-kraft [1]massbestämning [2]mass-luminositetsrelation [2]matematik i fysik [6]matematik, skriva [2]materia [6]Maxwells ekvationer [3]metabolism [3]metall, smältpunkt [3]meteorit [21]mikrovågsugn [25]Milankovitch cykler [3]mobiltelefon, strålning från [6]monstervåg [4]Monte Carlo-metoder [1]Mpemba-effekten [2]MRI [5]musikinstrument [19]månens bana [14]månens synbara storlek [1]månfärder [7]mörk energi [6]mörk materia [17]nanoteknik [6]Nationalencyklopedin [1]naturkonstant [7]naturlig radioaktivitet [3]nebulosa [13]NEO [10]neutrino [19]neutron [4]neutronstjärna [11]Newtons gravitationslag [12]Newtons rörelselagar [21]Newtons vagga [2]norrsken [7]nova [1]nyheter [11]Olbers paradox [2]orgelpipa [4]osmos [8]parallaxmetoden [4]parapsykologi [6]parbildning [7]Pascals lag [5]pauliprincipen [10]pendel, konisk [2]pendel, plan [9]PET [1]Plancks strålningslag [6]planet [17]planeters atmosfär [4]planeters form [3]plastfolie [1]polarisation [7]polaroidglasögon [3]potential/potentiell energi [30]prisma [1]projektarbete [1]pseudovetenskap [11]QED [7]radioaktiv datering [7]radioaktivitet, sönderfallskedja [7]radioaktivt sönderfall [38]radioteleskop [1]radon [4]raketekvationen [2]raketmotor [8]regn [1]regnbåge [6]relativistiskt massberoende [4]relativitetsteorin, allmänna [33]relativitetsteorin, speciella [45]religion [3]resistans [15]resistansförluster [2]resonans [5]richterskalan [2]ringklocka [5]rymddräkt [5]rymdfärder [23]rödförskjutning [7]röntgenrör [3]rörelseenergi [14]rörelsemängd [15]rörelsemängdsmoment [14]satellitbana [15]Saturnus´ ringar [6]schrödingerekvationen [4]Schrödingers katt [2]science fiction [6]segling [5]serie- och parallellkoppling [19]SETI [1]shareware [1]SI-enheter [6]skruvad boll [10]skymning [1]slumptal [1]SN 1987A [4]solaktivitet [2]solarkonstanten [6]solcell [7]solen [5]solen, avstånd till [1]solenergi [14]solens energiproduktion [9]solens utveckling [4]solförmörkelse [3]solsystemet [8]solsystemet, avstånd och rörelse [3]solsystemets bildande [12]specifik värmekapacitet [25]spegel [10]spektrum [11]standardmodellen [24]statisk elektricitet [12]stearinljuslåga [16]stjärna [4]stjärnhimlen [12]stjärnors utveckling [15]stroboskopeffekt [3]strålning, faror med [26]strålning, in-/ut- [6]strängteori [7]strömning [1]supernova [13]supertunga grundämnen [1]supraledning [7]svart hål [51]synvilla [6]sönderfallskonstant [5]teleskop [10]temperatur/temperaturskalor [17]temperaturstrålning [29]termodynamik [17]termometer [8]termos [3]Three Mile Island [3]tid [10]tidsdilatation [6]tidsekvation [4]tidvatten [15]tjerenkovstrålning [2]Tjernobyl [12]totalreflektion [9]transformator [6]transmutation av kärnavfall [2]trefas [3]trippelpunkt [2]tröghetsmoment [9]tsunami [5]tunneleffekt [3]TV [9]tvillingparadoxen [5]tyngdaccelerationen [16]tyngdlöshet [13]ultraljud [9]universums expansion [16]uppvärmning av bostäder [2]utvidgning [8]UV-ljus [13]vakuum [9]vatten/is [49]vattenkraft [7]vattenpump [2]vattenånga [2]Venus [11]verkningsgrad [26]vetenskaplig metod [18]Wikipedia [5]WIMPs [3]vindavkylning [4]vindenergi [12]Vintergatan [6]vridmoment [7]vulkanism [5]våg/partikelegenskaper [8]vågenergi [3]vågfunktion [2]värmemängd [3]värmepump/kylskåp [8]värmeöverföring/transport [46]väteatomen [2]vätskedroppsmodellen [5]växthuseffekten [36]ytspänning [18]årstider [4]ögat [18] (Enda villkor)
Definition:	(transmissions)mediumabsoluta nollpunktenabsorptionsspektraaccelerationackommodationackretionsskivaadiabatisk processaerodynamic heatingaerosolaggregationstillståndakustisk impedansallmänna gaslagenampereamperetimmeannihilationantigravitationantimateriaantropiska principenarbetearkimedes principasteroidasteroidbältetastigmatismastrobiologiastronomisk enhetatommassaatomnummeravogadros talbandspektrabatteribenhams snurrabergvärmebernoullis ekvationbetasönderfallbig bangbindningsenergibindningsenergibioluminiscensboltzmanns konstantbose–einstein-kondensatbrewstervinkelnbrownsk rörelsebrytningsindexbrännpunktbubbelkammarecarnotprocesscentrifugalkraftcentripetalkraftcirkumpolära stjärnorcitronbattericorioliskraftencurietemperaturendarwins evolutionsteoride broglie våglängdendecibeldeltonden kosmologiska principendensitetdielektrisk polarisationdielektriskt materialdiffus reflektiondiffusiondigitalkameradimensiondioptridiskret spektrumdispersiondopplereffektdotternukliddulong-petits lage=mc2ekliptikanekoekvivalensprincipenelasticitetelastisk energieldelektrisk dipolelektrisk laddningelektrisk spänningelektrisk strömelektriska fältstyrkanelektroluminiscenselektromagnetisk strålningelektroninfångningelektronskalelementarladdningenelementarpartiklaremissionsnebulosaemissionsspektraemsendoterm reaktionenergienergikällaenergiomvandlingenergipincipenenergipotentialentropi (makroskopisk definition)entropi (mikroskopisk definition)evighetsmaskinexciterade tillståndexoplanetexoterm reaktionextremofilerfallrörelsefaradays burfasdiagramfermats principferminivånferromagnetismfissionfjärde generationens reaktorfluidfluorescensflygplansvingeflykthastighetenfokalpunktfokusfosforescensfossila bränslenfotokromismfotomotståndfotonfotosfärenfotosyntesfouriers lagfraktalfranck-hertz försökfriktionfriktionskoefficientfritt fallfukushimafundamentala naturkrafternafusionfysikfysikaliska modellerfysiologifärgfärgblindhetfärgseendefönybara bränslenförnybara energikällorgaiagalaxgammastrålninggaskonstantengeneratorgeostationär satellitgeotermisk energiglobal uppvärmninggluonerglödlampagravitationgravitationengravitationskonstantengravitationsvågorgrundläggande fysikgrundtillståndetgrundtongrundämnegrå starrgränshastighetgula fläckenhalleffekthalogenlampahalveringstidhastighethawkingstrålningheisenbergs obestämdhetsrelationhertzsprung-russell diagramhiggspartikelnhookes laghornhinnanhubble ultra deep fieldhuygens principhydrostatiska paradoxenhägringhändelsehorisontenhästkrafthävstångicke-joniserande strålningideal gasimpedansinduktansinduktioninertialsysteminflationinfraljudinfraröd strålninginklinationinre konversioninre resistansinterferensinverterad populationisomerisospinnisoterm processisotoperjondriftjoniserande strålningjordfelsbrytarekalibreringkall fusionkalorikapacitanskapillärkraftenkastparabelkedjereaktionkemisk bindningkemisk bindningkemisk reaktionkemoluminiscenskeplers andra lagkeplers första lagkeplers tredje lagkilogramkirchhoffs lagkirchhoffs strålningslagkiselklassisk fysikklorofyllkokarreaktorkokpunktkolkornsmikrofonkometkomplementfärgkondensatorkonduktanskonservativ kraftkonserveringslagkontinuerligt spektrumkonvektionkoronankorrespondesprincipenkosmiska bakgrundsstrålningenkosmologikosmologiska rödskiftetkosmologiska standarmodellenkraftkristallkritisk densitetkritisk massakromosfärenkuiperbältetkundts rörkvantdatorkvantmekanikkvantmekanisk sammanflätningkvarkkvark-gluon plasmakvartskvasarkvasipartiklarkärnkrafterkärnreaktionkärnreaktorerkärnvapenlagrange-punkternalaserlenz lagleptonlila linjespektralivljudljusljusabsorptionljusbrytningljushastighetenljuskällorljusutbyteljusårlongitudinell våglorentzkraftenluftmotståndluminiscenslutande planlysdiodlysrörlågenergilampalägesenergilängdkontraktionmachomagnetismmagnuseffektenmarkradarmarkvärmemaskhålmassamasscentrummassdefektmassenhetmassexcessmasstalmateriamaxwell–boltzmannfördelningenmaxwells ekvationermedelvärdetmegaton tntmeissnereffektenmekanikens gyllene regelmerkurius periheliumprecessionmetafysikmetallbindningmetalldetektormetallicitetmeteormeteoritmeteoroidmilankovitch cyklermodern fysikmodernuklidmolmolekylmultiversummymetallmånemätfelmörk energimörk materiamörk nebulosamössbauer-effektennanometertekniknanopartikelnanotekniknationalencyklopedinnaturvetenskapnavigeringneoneutrinoneutrinooscillationerneutroninducerad fissionneutronstjärnanewtonnewtonringarnewtons andra lagnewtons avsvalningslagnewtons första lag (tröghetslagen)newtons gravitationslagnewtons tredje lagnobelpris i fysik 1925nobelpris i fysik 1993nobelpris i fysik 2015nobelpris i fysik 2017nobelpris i fysik 2020normalkraftennorrskennuklidnuklidkartanutida fysiknärsynthetockhams rakknivohms lagoorts kometmolnoregelbunden galaxosmosparapsykologiparbildningpascals princippauliprincipenperiodiska systemetplanck timeplancks strålningslagplanetplanetarisk nebulosaplasmaplasmaplasmaplasticitetpn-övergångpolarisationpolspänningpolär jetstrålepotentialproton-protonkedjanpseudovetenskapqcdqedradiative forcingradioaktivitetradioluminiscensraketekvationenrayleigh-spridningreaktansreflektionreflektionsnebulosarefraktionregnbågerelativ luftfuktighetrelativistisk energirelativistisk jetresistansresistivitetresistivitetresonansroche-gränsenrullmotståndrussells tekannarödförskjutningrörelseenergirörelsemängdrörelsemängdsmomentschwarzschildradiensekulär jämviktsekundsfärisk aberrationsi-enheternasingularitetsi-prefixsi-systemetsjälvinduktansskalärproduktskottsekundslipstreamslumpvisa mätfelsmältvärmesnells lagsolarkonstantensolcellersolenergisolens centrumsolförmörkelsesolkraftverksolvindsolvärmespallationspecifik värmekapacitetspektroskopispektrumspinnspontan fissionstandardavvikelsenstandardmodellenstatisk elektricitetstefan–boltzmanns lagstimulerad emissionstjärnastjärnbildstorhetstrålningstrålningstråloptiksträngteorinstående vågstämgaffelsublimationsupermassiva svarta hålsupernovasupertungt grundämnesuprafluiditetsupraledningsvart hålsvartkroppsvänghjulsystematiska mätfelsåpbubblasäkringsönderfallskedjasönderfallskonstantentemperaturtemperaturspektrumtemperaturstrålningtensortermodynamiktermodynamikens andra huvudsatstermodynamikens första huvudsatsthree mile islandtidtidens riktningtidsdilatationtidsekvationentidvattentidvattenkraftertillämpad fysiktjerenkovstrålningtjernobyltotalreflektiontransformatortransistortransparenstriboelektrisk effekttrippelpunktentrycktryckvattenreaktortröga massantröghettröghetsmomenttunga massantvillingparadoxentyngdtyngdaccelerationtyngdlöshettyngdpunktentyp ii supernovaufoultraljudultraviolett strålningultraviolettkatastrofenunderkylninguniversums åldervakuumvakuumfluktuationervakuumpolarisationvalenselektronvattenburen värmevattenkraftvattenkraftvattenångavektorerverkningsgradvetenskaplig metodwiens förskjutningslagwikipediaviktwimpvindkraftvintergatanvintergatanvirtuell bildvirtuell bildvit dvärgvoltvridmomentv-t diagramvåglängdenvåg-partikeldualitetvågtalvärmeledningvärmemängdvärmepumpvärmepumpvärmeöverföringvätebindningvätelika jonervätskedroppsmodellenväxthuseffektenytenergiångbildningsvärmeångtryckårstidernaåskaädelgasädelgaserögats linsöratöversynthetövertoner (Enda villkor)

---

Om du inte hittar svaret i databasen eller i

Sök i svenska Wikipedia:

Sök i Nationalencyklopedin

   

Sök med Google

   

- fråga gärna här.