Svar:
Jag har tagit mig friheten att slå ihop frågorna från Äppelviksskolan.

Det är svåra frågor ni ställer eftersom ni vill veta det historiska perspektivet. Det är en hel vetenskap som heter vetenskapshistoria, och det är vi inte experter på. Jag skall emellertid försöka mig på ett par kommentarer.

Relativitetsteorin publicerades av Einstein 1905. Här är originalversionen: Zur Elektrodynamik bewegter Körper. Artikeln är svårbegriplig för en modern fysiker, eftersom beteckningarna i formlerna är lite gammalmodiga och så är artikeln på tyska.
Vid den tiden var emellertid tyska mer vetenskapens språk än engelska, och tidens fysiker hade inga större problem att förstå artikeln.

Relativitetsteorin bygger i stort på ett antagande:
att ljushastigheten c i vakuum är konstant oberoende av hur man rör sig i förhÃ¥llande till ljusstrÃ¥len. Antagandet bygger pÃ¥ ett experiment som utfördes av Michelson-Morley 1887: History of Special Relativity. OvanstÃ¥ende artikel är mycket bra, och bör ha övertygat mÃ¥nga fysiker. Artikeln innehÃ¥ller nästan hela var vi kallar den Speciella relativitetsteorin utom det ni frÃ¥gar om, E=mc². Denna härleddes i en artikel publicerad senare under 1905: Does the Inertia of a Body Depend upon Its Energy-Content. Även denna artikel är svÃ¥rläst i dag (trots att den här är översatt till engelska). I artikeln finns en länk till en engelsk översättning av Einsteins första artikel om relativitetsteorin (Zur Elektrodynamik bewegter Körper).

Länk 1 nedan är Einstein själv som förklarar vad formeln innebär. Här är en artikel som ger ett par olika härledningar: Year of Physics 2005.

Exakta mätningar som bekräftade relativitetsteorin kom betydligt senare. Inte ens nobelkommittén var imponerad: nobelpriset Einstein fick 1921 var för hans förklaring av den fotoelektriska effekten (också 1905) och inte relativitetsteorin!

Tolkning: Ekvationen E=mc² skall tolkas sÃ¥ att massa och energi är ekvivalenta (utbytbara mot varandra) med "växlingskursen" c². Eftersom c är ganska stort motsvarar även en liten massa (eller mass-skillnad) en mycket stor energi.

Bekräftelsen pÃ¥ E=mc² kom först pÃ¥ 20/30-talet när man kunde mäta atommassor med hög precision, se frÃ¥ga [12726].

Det finns många böcker om relativitetsteorin och en bra artikel i Nationalencyklopedin. Wikipedia-artiklarna Einstein och Special_relativity är också mycket bra.

Se även fråga [20460].

/Peter E 2004-02-18

Svar:
Energin kommer från bindningenergin. En massa som faller ner i ett svart hål binds av gravitationsfältet på samma sätt som en elektron binds i en atom. Elektronen skickar ut ljus när den övergår till lägre tillstånd. Det kan även infallande materia i ett svart hål göra genom kollisioner och uppvärmning, men en massa som rör sig snabbt kan även sända ut gravitationsvågor.

Den energi som sänds ut som elektromagnetisk strålning eller gravitationsvågor är förlorad, så massan av det kompakta objektet minskar med detta belopp. Låt oss titta lite närmare på energiförhållandena.

Klassiskt (Newton) är flykthastigheten från en massa M med radien R är lika med ljushastigheten c när

R = R_S = 2GM/c²

(flykthastigheten är v = (2GM/r)^1/2, se fråga [3782]).
Gravitationell bindningsenergi för en massa m vid ytan (kallas händelsehorisonten eller Schwarzschild-radien) av ett svart hål blir då

GMm/R_S = mc²/2

vilket är exakt halva vilomassan mc². Om man i stället använder den allmänna relativitetsteorin (vilket vi självklart mÃ¥ste göra) blir uttrycket för händelsehorisonten oförändrad men den gravitationella bindningsenergin blir lika med vilomassan mc².

Hur skall vi tolka detta? Om vi lÃ¥ter en massa m falla ner i ett svart hÃ¥l kan vi frigöra maximalt energin mc²/2. Resten kommer att försvinna som rödförskjutning. Ett svart hÃ¥l är alltsÃ¥ en mycket effektiv energikälla - fusion frigör t.ex. bara nÃ¥gon procent av vilomassan. Detta är orsaken till att man tror att de mest energetiska objekten vi känner till, t.ex. kvasarer, är svarta hÃ¥l. Om energin frigöres när massan är vid händelsehorisonten blir rödskiftet oändligt, och ingen energi slipper ut. Om vi emellertid lÃ¥ter energin strÃ¥la ut när massan är pÃ¥ väg ner, sÃ¥ kan en del av energin slippa ut - maximalt mc²/2.

Länk 1 innehåller information från en expert på området. Länk 2 är en användbar formelsamling för svarta hål. Se även Black_hole och Supermassive_black_hole.
/Peter E 2005-12-16

Svar:
Frida! Som fysikaliskt teori måste relativitetsteorin anses mycket etablerad. Detta gäller både relativitetsteorin, speciella
och relativitetsteorin, allmänna. Se
Special_theory_of_relativityConsequences_derived_from_the_Lorentz_transformation och
General_theory_of_relativityConsequences_of_Einstein's_theory
för några experimentella resultat som stöder den speciella och den allmänna relativitetsteorin.

Det universiella navigeringssystemet GPS (se Global_Positioning_System och nedanstående figur från Wikimedia Commons) med 24 satelliter i bana runt jorden på en höjd av 20000 km skulle helt enkelt inte fungera om man inte tog hänsyn till relativitetsteorierna.

Dels orsakar banrörelsen att den mycket exakta klockan i en satellit saktar sig 7 mikrosekunder per dygn pga den speciella relativitetsteorin. Eftersom satelliten befinner sig i ett svagare gravitationsfält går klockan 45 mikrosekunder per dygn snabbare. Nettokorrektionen 45-7=38 mikrosekunder per dygn appliceras genom att man justerar klockan att gå lite långsammare innan satelliten skickas upp. Man synkroniserar även alla klockorna med hjälp av klockor på marken. Se vidare länk 1.

Se vidare Special_relativity och General_relativity.

---

Tillägg 5/4/2011:

Uppskattning av effekterna

Konstanter:

Ljushastigheten: c = 3.0010⁸ m/s

Gravitationskonstanten: G = 6.67510^-11m³/(kg.s²)

Jordens massa: M = 5.97410²⁴ kg

Jordens radie: R = 6.3710⁶ m

GPS-satelliternas avstÃ¥nd frÃ¥n jordens centrum (20000 km över jordytan): R_GPS = 26.3710⁶ m

Speciell relativitet

Vi räknar från jordens centrum eftersom satelliterna går ganska högt och jordens rotationshastighet är liten (mindre än 500 m/s) jämfört med satelliternas hastighet.

Satellitens hastighet v ges av

mv²/R_GPS = mMG/(R_GPS)²

vilket blir

v = sqrt(MG/R_GPS) = sqrt(5.9710²⁴6.6710^-11/(26.36710⁶) = 3886 m/s

Klockan påverkas med g-faktorn (Special_relativityTime_dilation_and_length_contraction)

g = sqrt(1-(v/c)²) =
sqrt(1-(3886/300000000)^2) = 0.9999999999161055

Den relativa korrektionen blir

1 - g = 8.38910^-11

och korrektionen på ett dygn blir

8.38910^-11606024 = 7.2510^-6 s

eller c:a 7 mikrosekunder.

Allmän relativitet

Denna korrektion har att göra med att man mÃ¥ste bevara totala energin även i ett gravitationsfält, se frÃ¥ga [16989], stycket gravitationell rödförskjutning. För att bevara energiprincipen mÃ¥ste tiden i ett starkt gravitationsfält gÃ¥ lÃ¥ngsammare än i ett svagare. Tiden gÃ¥r alltsÃ¥ till synes snabbare i GPS satelliterna än pÃ¥ jordytan. Den relativa korrektionen ges av potentialskillnaden dividerat med viloenergin mc² (m är satellitens massa som kommer att försvinna i slututtrycket).

Om gravitationspotentialen är U(r) så gäller genom integration av gravitationskraften

U(r) = -mMG/r

Ändringen i potentiell energi om vi går från jordytan till satellitbanan blir

DU = -mMG/R_GPS -(-mMG/R) = -mMG(1/R_GPS -1/R)

Med insatta värden blir

DU = m4.714 10⁷

Om vi dividerar detta med viloenergin mc² fÃ¥r vi den relativa korrektionen till

5.237 10^-10

PÃ¥ ett dygn blir korrektionen

5.237 10^-10246060 s = 45.2 mikrosekunder

vilket stämmer bra med värdet ovan.

/Peter E 2006-04-27

Svar:
Ljuset följer den snabbaste vägen som i ett gravitationsfält inte är en rät linje, se fråga [17427].

Det är ingalunda trivialt att räkna ut avböjningen. Man måste använda hela formalismen för den allmänna relativitetsteorin, se Two-body_problem_in_general_relativityApproximate_formula_for_the_bending_of_light.

Avböjningen vid solranden ges av uttrycket

df = 4GM/c²b

där G är gravitationskonstanten G = 6.674 10^-11 m³s^-2kg^-1

M är solens massa M = 1.989 10³⁰ kg

c är ljushastigheten c = 2.998 10⁸ m/s

b är solens radie b = 6.955 10⁸ m

Låt oss innan vi räknar ut df se vad den har för dimension

[df] = [m³s^-2kg^-1][kg]/([m²/s²][m]) = 1

dvs dimensionslöst som sig bör för en vinkel i radianer.

Vi får

df = 8.494 10^-6 radianer

Men 1 bågsekund är

2p/(3606060) = 4.848 10^-6 radianer.

Avböjningen i bågsekunder blir alltså

df = (8.494 10^-6)/(4.848 10^-6) = 1.75"

För att räkna på ett annat objekt, t.ex. ett svart hål, byter man bara ut massan M och radien b i formeln ovan.

Eddingtons mätningar vid solförmörkelsen 1919, nedanstående bild, (se Tests_of_general_relativity och länk 1) har ifrågasatts, men resultatet av mätningen har senare bekräftats. I vilket fall som helst innebar mätningarna en omedelbar acceptans av den allmänna relativitetsteorin från alla utom möjligen nobelpris-kommitteen.

/Peter E 2009-03-23

Svar:
Ali! Det var många svåra frågor. Låt oss börja med partikel-egenskaper. Jag tycker inte man skall föreställa sig en foton varken som en partikel eller en våg. En foton är en foton som lånat egenskaper både från partiklar och vågor.

Fotonens massa: Fotonen har energin E=hv. Eftersom energi och massa är ekvivalenta (E=mc²), sÃ¥ har fotonen massa. Man kan emellertid inte tala om fotonens vilomassa eftersom begreppet en stillastÃ¥ende foton saknar mening.

Experimentella bevis för att fotonen saknar vilomassa kommer bland annat frÃ¥n det faktum att den elektrostatiska kraften (Coulombs lag, som ju förklaras genom ett utbyte av virtuella fotoner) varierar som 1/r² En utbytespartikel med ändlig vilomassa hade givit ett annat avstÃ¥ndsberoende.

Se fråga [16939] för mer om historien bakom fotonbegreppet och länk 1 för en mer detaljerad framställning. Wikipedia-artikeln Photon är mycket bra, medan den svenska versionen är OK men inte särskilt omfattande: Foton.

Fotoner påverkas på två sätt av gravitationsfält:

1 Avböjning, t.ex. vid passage nära solen. Detta har behandlats ganska detaljerat i fråga [16021].

2 Gravitationell rödförskjutning.

Till skillnad frÃ¥n avböjning sÃ¥ kräver faktiskt en tillfredsställande behandling av gravitationell rödförskjutning bara enkel klassisk fysik och speciella relativitetsteorins E=mc². Börja med att studera den enkla animeringen under länk 2!

Den potentiella energin hos elektronerna i övre läget är (mgh)

2m_egH

Om vi förlänger med c² fÃ¥r vi

2m_ec²(gH/c²) = E_foton(gH/c²)

Vi fÃ¥r det relativa skiftet för höjdskillnaden 22.5 m (ref. ¹):

DE_foton/E_foton = gH/c² = 9.80322.5/(2.99810⁸)² = 2.454 10^-15

Det relativa skiftet har uppmätts (ref. ¹) med hjälp av mössbauerspektroskopi (se nedan) för 14.4 keV fotoner frÃ¥n ⁵⁷Co-sönderfall. Det uppmätta resultatet 2.451 10^-15 (med c:a 1% osäkerhet) är i bra överensstämmelse med detta.

Observera att det enda antagande vi gör är energins bevarande, vilket är en av fysikens grundläggande och mest etablerade lagar.

Observera även att man kan se skiftet till större våglängd (och därmed lägre frekvens) när fotonerna går uppåt är ekvivalent med att klockan går långsammare i ett starkare gravitationsfält.

Liknande experiment med hjälp av satelliter som sänder ut en mycket välbestämd frekvens har bekräftat Einsteins teori med en noggranhet bättre än 1 del pÃ¥ 10⁴.

Se vidare General_relativity, Gravitational_redshift och Pound-Rebka_experiment.

Se även http://fy.chalmers.se/~f1xjk/FysikaliskaPrinciper/FOREL.lp2/F16/F16.html

Mössbauerspektroskopi

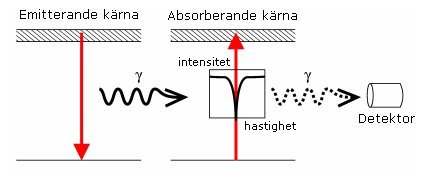
Mössbauer-effekten är rekylfri emission och absorption av gammastrålning från atomkärnor. När en atomkärna utsänder ett gammakvantum förloras i en del av energin till kärnans rekyl liksom vid absorption i en absorberande kärna. Detta eftersom både energi och rörelsemängd måste bevaras i processen.

I mössbauereffekten elimineras förlusterna dels genom att de radioaktiva kärnorna sitter i en kristall som tar upp rekylen, så att emission och absorption kan ske vid samma energi och dels genom att man kan kompensera energiförlusten genom att låta den utsändande kärnan röra sig.

Eftersom rekylen är mycket liten räcker det med en mycket måttlig hastighet på några mm/sekund, se nedanstående bild där det lilla diagrammet är en plot av ett mössbauerspektrum med hastighet på den horisontella axeln och observerad intensitet på den vertikala. Dippen i spektrum reflekterar det exciterade tillståndets vidd DE. Vidden är relaterad till tillståndets livslängd enligt Heisenbergs obestämdhetsrelation:

DE·Dt = h / 4p ~ 10^-34 Js

Se vidare Mössbauer_spectroscopy och mössbauer-effekten. Se även fråga [14685].
____________________________________________________________

¹ Pound and Snider, Physical Review Letters Vol 13, 18 (1964) 539

/Peter E 2010-03-15

Svar:
Oskar! Modellen som beskrivs i fråga [13733] - elektronfördelningen är som ett suddigt moln - är mer realistisk. Elektroner kan pga Heisenbergs obestämdhetsrelation inte stängas in i kärnan. Innan man upptäckte neutronen (1932) trodde man att atomkärnorna innehöll elektroner för att ge rätt kärnladdning. Det visade sig emellertid att obestämdhetsrelationen gjorde att elektroners rörelse inte kan begränsas till kärnan. När man upptäckt neutronen och förstått att en kärna består av Z protoner och N neutroner (där A=Z+N är masstalet) så var problemet löst: det krävdes inga elektroner i kärnan så de fick hålla sig på mycket större avstånd.

Oskar kom tillbaka med följande fråga:

Jag har försökt bli klok på varför man inte kan bestämma elektroners exakta position och varför de inte kan befinna sig i atomkärnan enligt Heisenbergs obestämdhetsrelation, men jag begriper mig inte på den. Kan ni förtydliga vad det egentligen obestämdhetsprincipen säger?

Oscar! Det var det konventionella svaret du fick, och jag håller med att jag kunde varit lite tydligare. Så låt oss först räkna lite.

Obestämdhetsrelationen ges av (Heisenberg_uncertainty_principle):

DxDp_x = h/4p (1)

Om vi stänger in en elektron i en atomkärna så är Dx ungefär 10^-15 m. Vi får då

Dp = 0.510^-34/10^-15 Js/m = 0.510^-19 Ns

För att få en bättre uppfattning om vad detta betyder gör vi om rörelsemängd p till energi E. Det relativistiska sambandet är (vi måste använda relativistiska samband eftersom hastigheten är hög)

E² = (pc)² + (mc²)² (2)

Eftersom energin kommer att visa sig vara mycket hög sÃ¥ kan vi försumma elektronens viloenergi mc² och fÃ¥r det enkla sambandet

E = pc (3)

(Detta är för övrigt även sambandet mellan energi och rörelsemängd för en foton.) Vi får

E = 0.510^-19310⁸ Nsm/s = 1.510^-11 J = 1.510^-11/(1.60210^-13) MeV = 100 MeV.

För det första kan vi konstatera att det var OK att försumma vilomassan för elektronen (0.511 MeV). För det andra ser vi att detta är en mycket hög energi och vi känner ingen kraft som är stark nog att hålla elektronen fångad. Coulombkraften räcker inte till på långa vägar - den ger det lägsta tillståndet (1s) i en atom på medelavståndet 10^-10 m, vilket är fem storleksordningar större än atomkärnans utsträckning.

Små system som atomer och kärnor följer alltså inte de lagar vi är vana vid i vardagen. Två olika laddade klot attraherar varandra och kommer att fastna vid varandra. Elektroner följer emellertid kvantmekanikens lagar och måste bland annat lyda Heisenbergs obestämdhetsrelation.

Det är emellertid inte helt lätt att tolka vad kvantmekaniken säger oss om naturen. Se t.ex. KvantmekanikExempel_p.C3.A5_tolkningar.

De flesta fysiker föredrar Köpenhamnstolkningen. Den sista, lite skämtsamma, "håll käft och räkna!" är inte heller så dum. Även om kvantmekaniken är svårförståelig så stämmer resultatet mycket bra med observationerna, och det är det viktigaste för en fysikalisk teori.

Länkarna 1 och 2 är svar på liknande frågor.

Man kan även resonera på ett annat sätt: om man stänger in elektronen i en låda om 210^-15 m så måste våglängden vara högst 410^-15 m (vågen måste ha en nod där potentialen blir oändlig). Vi får rörelsemängden

p = h/l = 6.6 10^-34/4 10^-15 = 2 10^-19 Ns

vilket är av samma storleksordning som ovan.
/Peter E 2010-05-23

Svar:
Frank! Det var Galileo Galilei som först utförde experiment och resonerade om detta, se Galileo_GalileiPhysics. Einstein använde ekvivalensen mellan acceleration och gravitation som ett grundantagande för sin allmänna relativitetsteori. Av detta följer direkt att alla kroppar faller lika snabbt i ett tyngdkraftfält. Man kan alltså byta ut ett tyngdkraftfält med en acceleration i motsatt riktning.

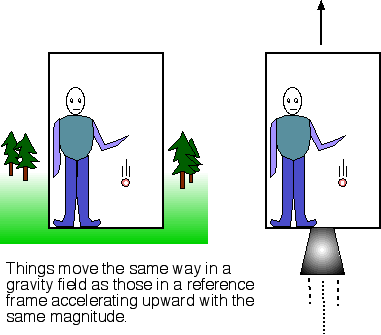
Låt oss säga du står i en hiss som befinner sig på marken (se nedanstående bild från länk 1). Du släpper ett föremål som faler nedåt. På grund av ovanstående ekvivalensprincip kan vi byta ut tyngdkraftfältet mot en lika stor acceleration uppåt. Det är uppenbart i detta fall (till höger i figuren) att fallhastigheten är helt oberoende av massan hos föremålet eftersom det ju står stilla (påverkas inte av någon kraft) medan hissen och du (som står på golvet) accelererar uppåt.

Se fråga [13663] för en kul demonstration.

Tillägg om ekvivalensprincipen

Engelska Wikipedia definierar ekvivalensprincipen som (Equivalence_principle):

In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's observation that the gravitational "force" as experienced locally while standing on a massive body (such as the Earth) is actually the same as the pseudo-force experienced by an observer in a non-inertial (accelerated) frame of reference.

Ekvivalensprincipen förekommer även i en svagare form i klassisk newtonsk fysik: ekvivalensen mellan tung och trög massa, dvs att massan m som förekommer i uttrycket

F = m a

är samma som förekommer i Newtons gravitationslag

F = G M m/r²

dvs accelerationen a ges av

a = G M/r²

oberoende av m.

Av detta följer att alla föremål faller med samma acceleration i ett gravitationsfält (bortsett från luftmotståndet).

Länk 2 innehåller Galileis teoretiska argumentation för ekvivalensprincipen. Se A Cultural History of Gravity and the Equivalence Principle för diskussion om tidigare funderingar (den Bysantinske filosofen Iohannes Philiponus).

/Peter E 2010-09-05

Svar:
Hej Thomas! Du syftar på artikeln under länk 1. Att man behöver relativistiska korrektioner vid beräkningar av atomära nivåer är inget nytt. Detta gäller särskilt de innersta skalen. Det är däremot lite förvånande att relativitetskorrektionerna har så stor påverkan på elektriska egenskaper som ju styrs av de yttre skalen. Mer om detta nedan.

Som alltid vill jag emellertid varna för modellen att elektronerna är små laddade kulor som snurrar i banor kring kärnan och riskerar falla ner i densamma, se fråga [13733] och [17237]. Verkligheten är såpass annorlunda de bilder vi kan föreställa oss eftersom vår erfarenhet kommer från den makroskopiska världen där partiklar och vågor uppför sig "normalt".

För att "förstå" atomära system löser man en ekvation, schrödingerekvationen (SE), se Schrödinger_equation. För atomer som är mer komplexa än väteatomen är det inte trivialt att lösa SE och man tvingas till approximationer och omfattande iterativa processer.

SE tar inte hänsyn till relativistiska effekter, t.ex. att en elektrons massa beror av dess hastighet (speciella relativitetsteorin). Diracekvationen (Dirac_equation) gör emellertid detta. Problemet är att den är ännu mer svårhanterlig.

Artikeln från Uppsala universitet (länk 2 är en light-version, originalartikeln är bitvis rätt svår att förstå för icke-specialister) redovisar en beräkning av energinivåerna i bly både icke-relativistiskt och relativistiskt. Man kan med den relativistiska lösningen mycket bra reproducera EMS (fråga [17476]) för ett blybatteri. Den icke-relativistiska lösningen avviker emellertid väsentligt från de c:a 2V man observerar.

För tenn (som ligger ovanför bly i det periodiska systemet och borde likna bly) är den relativistiska effekten mycket mindre, vilket medför att tennbatterier är ganska värdelösa eftersom EMS är mycket liten. Anledningen är att tenn har betydligt lägre kärnladdning än bly (50 respektive 82), vilket innebär att elektronerna rör sig långsammare i tenn.

Det visar sig från räkningarna att det är framför allt 6s nivåerna (6s är bland valens-nivåerna i bly) som påverkas av relativistiska effekter. Eftersom s motsvarar rörelsemängdsmomentet 0 har dessa elektroner en liten men dock sannolikhet att befinna sig nära atomkärnan. På grund av blys höga kärnladdning rör de sig då mycket snabbt, och relativistiska effekter blir stora. Ökningen i elektronens massa gör att orbitalen krymper och fördelningen hos elektronmolnet förskjuts in mot kärnan.

Sammanfattningsvis beror effekten på att relativistiska effekter för elektroner nära blykärnan påverkar valensnivåerna, vilka i sin tur bestämmer EMS för blybatteriet.

Jag tycker artikeln är intressant av flera skäl:

• Att man med grundläggande kvantmekanik kan beräkna makroskopiska storheter.
  
• Relativistiska effekter är inte alltid smÃ¥ och knappt mätbara korrektioner.
  
• Att man kan räkna pÃ¥ molekyler och joner.
  

Den relativistiska kontraktionen av 6s orbitalen förklarar även varför guld glimmar gult och varför guld är så lite reaktivt: What Gives Gold that Mellow Glow?. Se fråga [14685] för fler experimentella stöd för den speciella och allmänna relatiovitetsteorin.

Slutligen kan jag inte låta bli att citera den avslutande meningen i artikeln: Finally, we note that cars start due to relativity :-).
/Peter E 2011-01-27

Svar:
Du refererar till ämnet för pressreleasen under länk 1. Felet i den urspungliga mätningen är nu lokaliserat, se Hade Einstein fel?, så problemet med neutriner som rör sig snabbare än ljuset är löst.

En av forskningsgrupperna på CERN (OPERA-kollaborationen) har mätt löptiden hos neutriner från CERN till gruvan Gran Sasso 73 mil ner i Italien. Totalt har man detekterat c:a 16000 neutriner. Resultatet är att man får en hastighet som är lite överstigande ljushastigheten i vakuum c. Resultatet är signifikant med 6 standardavvikelser.

Löpsträckan pÃ¥ 73 mil (löptid 2.4 millisekunder med ljushastigheten) bestämdes med GPS med en precision pÃ¥ 20 cm. Tidssynkroniseringen gjordes även den med GPS och hade en precision av 1 ns. Totala osäkerheten i tidsdata uppskattades till 10 ns, och den uppmätta effekten var 60 ns. Denna diskrepans pÃ¥ 60 ns motsvarar t.ex. ett fel i avstÃ¥ndsmätningen pÃ¥ 6010^-9310⁸ = 18 m.

Vad gäller mätningen av löpsträckan var den största svårigheten att mäta sträckan inne i tunneln i gruvan Gran Sasso - GPSen fungerar dåligt under 1400 m berg! Man kan i mätningarna (som pågått sedan 2009) tydligt se effekter av kontinentaldriften och ett hopp i samband med en jordbävning i Italien 2009, se nedanstående figur.

Man gav ett webbseminarium från CERN fredagen den 23 aeptember 2011, länk 2. Där presenterade man resultatet och metoderna mycket bra och detaljerat.

Kommentarer:

De flesta fysiker tror nog att mätningen är felaktig, men än så länge finns ingen bra förklaring. Troligaste orsaken är att sträckan är felmätt eller att tidssynkroniseringen CERN-Gran Sassio är felaktig.

Einsteins speciella relativitetsteori förbjuder inte expicivt att partiklar rör sig med överljushastighet. Vad den förbjuder är att en partikel accelereras upp till ljushastigheten, det skulle kosta oändlig energi. Enda problemet är att partiklar som rör sig snabbare än ljuset (hypotetiska partiklar som kallas tachyoner, se Tachyon) får imaginär massa. Se även fråga [15804].

OPERA-kollaborationen har helt följt god vetenskaplig procedur:

- Analysen har gjorts "blind" så att man inte skulle kunna påverkas av det väntade resultatet.

- Arbetet presenterades utförligt på ett öppet seminarium och i ett publicerat preprint.

Det är inte första gången man försökt mäta neutriners hastighet, men man har inte fått fram definitiva värden. Den enda signifikanta observationen hittills är neutriner från supernovan SN 1987A, se fråga [125] och Supernova_1987A. Denna mätning visar att neutrinernas hastighet är mycket nära ljushastigheten. Att neutrinerna kom fram några timmar före ljuset kan förklaras att stjärnan är transparent för neutriner tidigare än den är transparent för ljus. Avståndet till SN 1987A är 168000 ljusår. Med den uppmätta tidsdifferensen skulle neutrinerna ha kommit fram

(6010^-9/2.410^-3)168000 = 4.2 år före ljuset.

Neutrinerna skulle alltså kommit fram flera år innan supernovan upptäcktes, inte några timmar. Tyvärr var neutrinodetektorerna inte igång då (Kamiokande II började ta data 1985, se (Kamioka_Observatory).

_____________________________________________________________________

Fotnot: Nedanstående meddelande distribuerades i samband med pressreleasen. Det får anses helt unikt att en officiell deklaration från CERN går ut tillsammans med en pressrelease.

Dear Colleagues,

As usual, I am sending you this CERN press release before we issue it
to the media. Unusually this time, however, I feel that it needs a few
words of introduction. The OPERA collaboration has measured the time
of flight of neutrinos sent from CERN to Gran Sasso, along with the
distance they cover. These measurements appear to show that the
neutrinos are travelling faster than light. When a collaboration makes
a surprising observation such as this and is unable to account for it,
the ethics of Science demand that the results be made available to a
wider community, to seek scrutiny and to encourage independent
experiments. That's why when the spokesperson of the OPERA
collaboration asked me whether they could hold a seminar here, I said yes. Given the potential impact of such a measurement, I felt it important for CERN formally to make its position clear. That's the reason for the cautiously worded statement we're sending to the media today.

Best regards,

Rolf Heuer

Se även Hade Einstein fel? där det längst ner finns en uppdatering av statusen för experimentet.

/Peter E 2011-09-23

Svar:
Engelska Wikipedia säger följande om elektromagnetisk strålning:

Electromagnetic radiation (EMR) is a form of radiant energy released by certain electromagnetic processes. Visible light is one type of electromagnetic radiation, other familiar forms are invisible electromagnetic radiations such as X-rays and radio waves.

Classically, EMR consists of electromagnetic waves, which are synchronized oscillations of electric and magnetic fields that propagate at the speed of light. The oscillations of the two fields are perpendicular to each other and perpendicular to the direction of energy and wave propagation, forming a transverse wave. Electromagnetic waves can be characterized by either the frequency or wavelength of their oscillations to form the electromagnetic spectrum. (Electromagnetic_radiation)

Maxwells ekvationer ger en vågekvation där amplituden på stort avstånd från källan (se nedanstående figur) avtar som 1/r. Detta är ditt strålningsfält. Fälten ser ut som i figuren i fråga [15035]. Man ser att E och B svänger i takt.

Nära källan är fälten mycket mer komplicerade eftersom vi har både laddningar och magnetism. Dessa (induktionsfältet) avtar emellertid hastigare än 1/r och försvinner på stort avstånd. Det är alltså bara strålningsfältet, som avtar som 1/r, som överlever på stort avstånd.

Det är alltså amplituden på fälten som avtar som 1/r. Energitransporten ges emellertid av Poyntings vektor (Poynting_vectorPlane_waves):

P = konstExB = konstE²/c,

och avtar, som sig bör, som 1/r².

Se även Electromagnetic_radiationNear_and_far_fields, Electromagnetic_radiationDerivation_from_electromagnetic_theory och fråga [2867].

Hoppas det blev lite klarare, Rose, men detta är inte helt lätt. Bra föreläsningar om Maxwells ekvationer och elektromagnetisk strålning av professor Shankar (Yale) finns under länk 1 och 2. Mot slutet av föreläsning 2 visar föreläsaren hur den magnetiska kraften uppkommer som en relativistisk effekt på laddningar som rör sig. Det var detta som fick Einstein att utveckla sin speciella relativitetsteori.

/Peter E 2015-03-14