Vill du ha ett snabbt svar - sök i databasen
Nyckelord: speciella
12 träffar
Fråga:
Om två bilar åker ifrånvarandra med hastigeterna 75 km/h. Då avlägsnar ju
dom sig från varandra med 150 km/h
Om två "planeter" åker i från varandra med 60% av ljusets hastighet
då kan do ju inte avlägsna sig från varandra med 120 % av ljusetshastiget.
Hur gör man för att räkna ut det?
/Markus H, Dergården, Lerum 1997-11-09
Om två bilar åker ifrånvarandra med hastigeterna 75 km/h. Då avlägsnar ju
dom sig från varandra med 150 km/h
Om två "planeter" åker i från varandra med 60% av ljusets hastighet
då kan do ju inte avlägsna sig från varandra med 120 % av ljusetshastiget.
Hur gör man för att räkna ut det?
/Markus H, Dergården, Lerum 1997-11-09
Svar:
Man får använda "Einsteins formel för addition av hastigheter" som
bygger på den speciella relativitetsteorin. Om vi kallar
hastigheterna v1 och v2, så blir det relativa hastigheten
(v1+v2)/(1+v1v2/c2).
För
ditt exempel v1=v2=0.6c blir resultatet 1.2c/(1+0.36)=0.88c.
Observera att om en av hastigheterna är c blir den relativa hastigheten
(c+v2)/(1+cv2/c2) = (c+v2)/(1+v2/c) = c(c+v2)/(c+v2) = c
alltså summan blir aldrig högre än c.
/Peter Ekström 1997-11-22
Man får använda "Einsteins formel för addition av hastigheter" som
bygger på den speciella relativitetsteorin. Om vi kallar
hastigheterna v1 och v2, så blir det relativa hastigheten
(v1+v2)/(1+v1v2/c2).
För
ditt exempel v1=v2=0.6c blir resultatet 1.2c/(1+0.36)=0.88c.
Observera att om en av hastigheterna är c blir den relativa hastigheten
(c+v2)/(1+cv2/c2) = (c+v2)/(1+v2/c) = c(c+v2)/(c+v2) = c
alltså summan blir aldrig högre än c.
/Peter Ekström 1997-11-22
Fråga:
Jag vill veta vad det finns för några bevis för
att relativitetsteorin stämmer. Jag vill också veta var
jag kan läsa ingående om dessa bevis.
/Gustav A, Alströmergymnasiet, Alingsås 1998-02-27
Jag vill veta vad det finns för några bevis för
att relativitetsteorin stämmer. Jag vill också veta var
jag kan läsa ingående om dessa bevis.
/Gustav A, Alströmergymnasiet, Alingsås 1998-02-27
Svar:
Det finns många både direkta och indirekta bevis för Einsteins relativitetsteori. Den speciella relativitetsteorin behandlar tid och rum samt energi och massa. Där
finns det bland annat följande bevis:
Den allmänna relativitetsteorin handlar om gravitationen och hur den påverkar rummets krökning. Bevisen kommer här från astrofysiken:
Listan kan göras mycket längre. Läs någon av de populära böcker som finns om relativitetsteorin, till exempel "Einsteins universum" av Calder. Se även Allmän relativitetsteori och kosmologi .
.
/GO 1999-06-27
Det finns många både direkta och indirekta bevis för Einsteins relativitetsteori. Den speciella relativitetsteorin behandlar tid och rum samt energi och massa. Där
finns det bland annat följande bevis:
- Tiden går långsammare för partiklar i rörelse. Detta har bevisats i en mängd experiment i partikelacceleratorer och för myoner från kosmisk strålning (se fråga [2697]).
- Massans och energins ekvivalens har bevisats i kärnfysiken där man kan mäta både massa och energi för olika atomkärnor.
Den allmänna relativitetsteorin handlar om gravitationen och hur den påverkar rummets krökning. Bevisen kommer här från astrofysiken:
- Man har upptäckt svarta hål som förutsägs av teorin.
- Dubbelstjärnesystem förlorar energi i enlighet med teorins förutsägelser, se fråga [473].
Listan kan göras mycket längre. Läs någon av de populära böcker som finns om relativitetsteorin, till exempel "Einsteins universum" av Calder. Se även Allmän relativitetsteori och kosmologi
/GO 1999-06-27
Fråga:
Jo, jag ska hålla ett litet föredrag om RELATIVITETSTEORIN. Ett ämne som kanske inte är det lättaste. Jag har samlat lagom med teoretisk fakta, men skulle vilja ha ett experiment som grädde på toppen. Har ni förslag på hur man kan visa att tidsdilatationen verkligen fungerar?
/Markus A, Komvux, Sjöbo, Sjöbo 1999-02-08
Jo, jag ska hålla ett litet föredrag om RELATIVITETSTEORIN. Ett ämne som kanske inte är det lättaste. Jag har samlat lagom med teoretisk fakta, men skulle vilja ha ett experiment som grädde på toppen. Har ni förslag på hur man kan visa att tidsdilatationen verkligen fungerar?
/Markus A, Komvux, Sjöbo, Sjöbo 1999-02-08
Svar:
Kanske inte ett experiment, men ett bra exempel.
Först ett par definitioner:
Längdkontraktion är den minskning i längd som enligt Albert Einsteins speciella relativititetsteori uppstår när ett föremål rör sig med stor hastighet i förhållande till den som mäter längden. Vid mer vardagsnära hastigheter är denna längdminskning helt försumbar. Det är först vid hastigheter som är minst 1/10 av ljusets hastighet som den får någon märkbar betydelse.
Tidsdilatation (tidsutvidgning) beroende på hastighet innebär att om två referenssystem r och r', har identiska klockor, kommer en observatör i r att anse att klockan i r' går långsammare om referenssystemen r och r' befinner sig i relativ rörelse. En observatör i r' anser likaså att klockan i r går långsammare än den lokala klockan.
Kosmiska strålningen består huvudsakligen av atomkärnor med mycket höga energier (mest väte). När de kolliderar med luften på cirka 20 km höjd, uppstår en uppsjö av olika partiklar. De flesta är kortlivade och sönderfaller snabbt. En av sönderfallsprodukterna kallas myon, och på grund av sina egenskaper, är den mycket lite benägen att kollidera med kärnorna i luften. Den försvinner för det mesta genom att den sönderfaller. Hur långt går den?
Myonens medellivslängd är 2.210-6 s. Antag att den går nära ljushastigheten (300000 km/s). Då får vi en sträcka på
300000 2.210-6 = 0.6 km = 660 m.
Ändå är det så, att de flesta partiklar vi kan registrera här nere är myoner. Genom en människa far det typiskt 30 - 40 högenergetiska myoner varje sekund. De överlever hit ner på grund av tidsdilatationen. De har så hög hastighet att tiden går mycket långsammare för dem, se översta formeln i bilden nedan. En myon med en Lorentz-faktor på 1000 kan i princip gå 660 km. Sådana myoner är inte alls ovanliga. För den myonen går tiden 1000 gånger långsammare (från oss sett).
Jaha, OK men sett från myonen då? Där går ju tiden med "normal" hastighet och myonen kan väl inte hinna ner till markytan innan den sönderfaller? Jo, det gör den därför att längdkontraktionen, se nedersta formeln nedan, gör att den sträcka myonen måste tillryggalägga är mycket kortare (sett ur myonens perspektiv).
Det är klart att resultatet att myonen hinner ner till marken innan den sönderfaller måste vara samma oberoende av om vi betraktar myonen från marken eller om vi följer med den ner genom luften.
Se vidareMuon , Time_dilation och Length_contraction .
Kanske inte ett experiment, men ett bra exempel.
Först ett par definitioner:
Kosmiska strålningen består huvudsakligen av atomkärnor med mycket höga energier (mest väte). När de kolliderar med luften på cirka 20 km höjd, uppstår en uppsjö av olika partiklar. De flesta är kortlivade och sönderfaller snabbt. En av sönderfallsprodukterna kallas myon, och på grund av sina egenskaper, är den mycket lite benägen att kollidera med kärnorna i luften. Den försvinner för det mesta genom att den sönderfaller. Hur långt går den?
Myonens medellivslängd är 2.210-6 s. Antag att den går nära ljushastigheten (300000 km/s). Då får vi en sträcka på
300000 2.210-6 = 0.6 km = 660 m.
Ändå är det så, att de flesta partiklar vi kan registrera här nere är myoner. Genom en människa far det typiskt 30 - 40 högenergetiska myoner varje sekund. De överlever hit ner på grund av tidsdilatationen. De har så hög hastighet att tiden går mycket långsammare för dem, se översta formeln i bilden nedan. En myon med en Lorentz-faktor på 1000 kan i princip gå 660 km. Sådana myoner är inte alls ovanliga. För den myonen går tiden 1000 gånger långsammare (från oss sett).
Jaha, OK men sett från myonen då? Där går ju tiden med "normal" hastighet och myonen kan väl inte hinna ner till markytan innan den sönderfaller? Jo, det gör den därför att längdkontraktionen, se nedersta formeln nedan, gör att den sträcka myonen måste tillryggalägga är mycket kortare (sett ur myonens perspektiv).
Det är klart att resultatet att myonen hinner ner till marken innan den sönderfaller måste vara samma oberoende av om vi betraktar myonen från marken eller om vi följer med den ner genom luften.
Se vidare
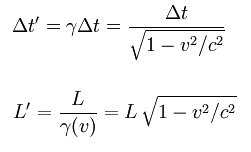
Fråga:
En fråga har dykt opp om relativitetsteori:
Observatör A står stilla på marken vid en järnvägstunnel. Observatör B åker i ett tåg med samma vilolängd som tunneln. Tåget rör sig relativt A med en hastighet nära ljusets.
På rälsen finns två strömbrytare, en alldeles före och en alldeles
efter tunneln. En sådan trycks ner om någon del av tåget befinner sig ovanför (alltså inte bara när själva hjulen passerar). Strömbrytarna är seriekopplade i en krets med ett batteri och en lampa som alltså lyser bara då båda strömbrytarna är nertryckta.
P g a längdkontraktion tycker B att tåget är längre än tunneln och att båda strömbrytarna därför är nertryckta samtidigt en liten stund. Lampan torde alltså lysa för honom.
För A däremot är tåget kortare än tunneln och lampan lyser inte!
Men om lampan lyser för den ene måste den lysa för den andre också
- det är ju invariant och oberoende av observatör.
Kan du hitta felet i resonemanget?
Lyser lampan?
/Jonas S, Spånga gymnasium, Spånga 1999-03-17
En fråga har dykt opp om relativitetsteori:
Observatör A står stilla på marken vid en järnvägstunnel. Observatör B åker i ett tåg med samma vilolängd som tunneln. Tåget rör sig relativt A med en hastighet nära ljusets.
På rälsen finns två strömbrytare, en alldeles före och en alldeles
efter tunneln. En sådan trycks ner om någon del av tåget befinner sig ovanför (alltså inte bara när själva hjulen passerar). Strömbrytarna är seriekopplade i en krets med ett batteri och en lampa som alltså lyser bara då båda strömbrytarna är nertryckta.
P g a längdkontraktion tycker B att tåget är längre än tunneln och att båda strömbrytarna därför är nertryckta samtidigt en liten stund. Lampan torde alltså lysa för honom.
För A däremot är tåget kortare än tunneln och lampan lyser inte!
Men om lampan lyser för den ene måste den lysa för den andre också
- det är ju invariant och oberoende av observatör.
Kan du hitta felet i resonemanget?
Lyser lampan?
/Jonas S, Spånga gymnasium, Spånga 1999-03-17
Svar:
Haken i resonemanget är det där lilla ordet samtidigt, som man
måste vara mycket noga med hur man använder i relativitetsteorin.
Det var just med en analys av detta begrepp, som Einstein inledde
sin berömda artikel från 1905, se fråga [12753]. Man kan inte använda det ordet som
vi är vana i vardagstillvaron.
Signalerna från brytarna måste ju transporteras till lampan, och
det kan ju inte gå fortare än ljuset. Beroende på vilken transporthastighet man antar, tågets hastighet och lampans placering
får man olika resultat. Det går i varje fall att analysera situationen,
så att resultatet blir det samma, sett från tunneln och tåget.
Tillägg 21/4/08:
Länk 1 nedan 'The Train and The Twins' diskuterar tågparadoxen (ytligt) och tvillingparadoxen ingående. Länk 2 (Storrs McCall & E. J. Lowe: 3D/4D equivalence, the twins paradox and
absolute time) säger att tågparadoxen endast kan lösas om man betraktar problemet i full rymd-tid 4D. Problemet är en perspektiveffekt. Se även diskussion i Taylor/Wheeler: Spacetime Physics. Det finns för övrigt flera varianter av tåg-tunnelparadoxen: en linjal och lucka i bordet, en hoppstav och en lada mm.
/KS/lpe 1999-03-18
Haken i resonemanget är det där lilla ordet samtidigt, som man
måste vara mycket noga med hur man använder i relativitetsteorin.
Det var just med en analys av detta begrepp, som Einstein inledde
sin berömda artikel från 1905, se fråga [12753]. Man kan inte använda det ordet som
vi är vana i vardagstillvaron.
Signalerna från brytarna måste ju transporteras till lampan, och
det kan ju inte gå fortare än ljuset. Beroende på vilken transporthastighet man antar, tågets hastighet och lampans placering
får man olika resultat. Det går i varje fall att analysera situationen,
så att resultatet blir det samma, sett från tunneln och tåget.
Tillägg 21/4/08:
Länk 1 nedan 'The Train and The Twins' diskuterar tågparadoxen (ytligt) och tvillingparadoxen ingående. Länk 2 (Storrs McCall & E. J. Lowe: 3D/4D equivalence, the twins paradox and
absolute time) säger att tågparadoxen endast kan lösas om man betraktar problemet i full rymd-tid 4D. Problemet är en perspektiveffekt. Se även diskussion i Taylor/Wheeler: Spacetime Physics. Det finns för övrigt flera varianter av tåg-tunnelparadoxen: en linjal och lucka i bordet, en hoppstav och en lada mm.
/KS/lpe 1999-03-18
Fråga:
Snabbare än ljuset?
Om man skulle tillverka en rak stolpe som är 1 ljusår lång och jag står
på ena sidan och knuffar den fram och tillbaka, skulle inte andra änden
röra sig samtidigt då?
/Magnus J, 2001-01-29
Snabbare än ljuset?
Om man skulle tillverka en rak stolpe som är 1 ljusår lång och jag står
på ena sidan och knuffar den fram och tillbaka, skulle inte andra änden
röra sig samtidigt då?
/Magnus J, 2001-01-29
Svar:
Om du rycker i stången fortplantar sig "rycket" med ljudets hastighet.
Antag att ljudhastigheten i stången är 1 km/s. I ditt exempel tar det
då 300000 år för "rycket" att nå andra änden. Ljushastigheten är ju
300000 km/s. Enligt den speciella relativitetsteorin finns inga stela
kroppar.
/KS 2001-01-30
Om du rycker i stången fortplantar sig "rycket" med ljudets hastighet.
Antag att ljudhastigheten i stången är 1 km/s. I ditt exempel tar det
då 300000 år för "rycket" att nå andra änden. Ljushastigheten är ju
300000 km/s. Enligt den speciella relativitetsteorin finns inga stela
kroppar.
/KS 2001-01-30
Fråga:
Hej!
Undrar lite om skillnaderna mellan den klassiska fysiken och Einsteins två
relativitetsteorier. T.ex. innan dessa var det allmänt accepterat att
och rum var absolut, men dessa postulat motbevisades av Einstein och
förändrade vårt sätt att betrakta universum!
Nu undrar jag vilka andra fenomen som den klassiska fysiken inte kunde förklara,
fick sina förklaringar genom Einsteins eminenta teorier? Vore tacksam för svar.
/Magnus A, Köping 2001-12-07
Hej!
Undrar lite om skillnaderna mellan den klassiska fysiken och Einsteins två
relativitetsteorier. T.ex. innan dessa var det allmänt accepterat att
och rum var absolut, men dessa postulat motbevisades av Einstein och
förändrade vårt sätt att betrakta universum!
Nu undrar jag vilka andra fenomen som den klassiska fysiken inte kunde förklara,
fick sina förklaringar genom Einsteins eminenta teorier? Vore tacksam för svar.
/Magnus A, Köping 2001-12-07
Svar:
Valet av ordet "relativitetsteori" är lite olyckligt. Ofta får man höra
att den innebär att "allt är relativt", vilket är en missuppfattning.
Både Newtons
och Einsteins teori (från 1905) är relativitetsteorier i den mening, att
relativitetsprincipen gäller i båda.
Denna säger att fysiken är densamma
i inertialsystem, alltså system i likformig rörelse.
Den viktiga skillnaden är, att Einstein utgår ifrån, att ljushastigheten i
vakuum är konstant och oberoende av inertialsystemet. Vidare utgår han
ifrån att energi och information inte kan förflytta sig snabbare
än ljuset.
Det leder till att
begrepp som tid, längd och samtidighet inte fungerar enligt vår
vardagsuppfattning. Det leder också till den välkända relationen
mellan energi och massa
E = mc2.
Den allmänna relativitetsteorin är huvudsakligen en gravitationsteori,
baserad på den speciella relativitesteorin. Här inför man
ekvivalensprincipen, som säger att den tunga massan är lika med den
tröga massan. Den första har med gravitation att göra, den andra med
acceleration. Gravitationskraften (liksom centrifugalkraften) betraktas
här som en fiktiv kraft, alltså en kraft som egentligen inte behövs.
Partiklar som inte påverkas av någon kraft, rör sig "rätlinjigt" i den
krökta fyrdimensionella rumstiden. En satellit som rör sig i en bana
runt jorden, rör sig i någon mening "rätlinjigt" i den rumstid, som
kröks av jordens massa.
Att gå in på alla fenomen, som förklaras av Einsteins teorier skulle dra
alldeles för långt. Man kan i alla fall konstatera, att inga exerimentella
data strider mot teorierna. Sedan vill vi påpeka, att man inte kan säga
att Newtons mekanik är fel. Under mindre extrema förhållanden duger
den utmärkt. När man skickar sonder till Mars, använder man Newtons mekanik.
/KS 2001-12-10
Valet av ordet "relativitetsteori" är lite olyckligt. Ofta får man höra
att den innebär att "allt är relativt", vilket är en missuppfattning.
Både Newtons
och Einsteins teori (från 1905) är relativitetsteorier i den mening, att
relativitetsprincipen gäller i båda.
Denna säger att fysiken är densamma
i inertialsystem, alltså system i likformig rörelse.
Den viktiga skillnaden är, att Einstein utgår ifrån, att ljushastigheten i
vakuum är konstant och oberoende av inertialsystemet. Vidare utgår han
ifrån att energi och information inte kan förflytta sig snabbare
än ljuset.
Det leder till att
begrepp som tid, längd och samtidighet inte fungerar enligt vår
vardagsuppfattning. Det leder också till den välkända relationen
mellan energi och massa
E = mc2.
Den allmänna relativitetsteorin är huvudsakligen en gravitationsteori,
baserad på den speciella relativitesteorin. Här inför man
ekvivalensprincipen, som säger att den tunga massan är lika med den
tröga massan. Den första har med gravitation att göra, den andra med
acceleration. Gravitationskraften (liksom centrifugalkraften) betraktas
här som en fiktiv kraft, alltså en kraft som egentligen inte behövs.
Partiklar som inte påverkas av någon kraft, rör sig "rätlinjigt" i den
krökta fyrdimensionella rumstiden. En satellit som rör sig i en bana
runt jorden, rör sig i någon mening "rätlinjigt" i den rumstid, som
kröks av jordens massa.
Att gå in på alla fenomen, som förklaras av Einsteins teorier skulle dra
alldeles för långt. Man kan i alla fall konstatera, att inga exerimentella
data strider mot teorierna. Sedan vill vi påpeka, att man inte kan säga
att Newtons mekanik är fel. Under mindre extrema förhållanden duger
den utmärkt. När man skickar sonder till Mars, använder man Newtons mekanik.
/KS 2001-12-10
Hur kom Einstein på formeln E=mc2?
Fråga:
Jag har en fråga om formeln E=mc2. Jag undrar lite över hur folk (fysiker) reagerade när formeln publicerades. Var man skeptiska eller lyriska? Trodde man på att den verkligen fungerade från början?
Hur kom Einstein på formeln E=mc2? Var det en slump, eller inte?
(Henrik A)
Fungerar alltid Einsteins formel E=mc2? Vad använder man den till? (Erik D)
/Niklas N, Äppelviken, Bromma 2004-02-17
Jag har en fråga om formeln E=mc2. Jag undrar lite över hur folk (fysiker) reagerade när formeln publicerades. Var man skeptiska eller lyriska? Trodde man på att den verkligen fungerade från början?
Hur kom Einstein på formeln E=mc2? Var det en slump, eller inte?
(Henrik A)
Fungerar alltid Einsteins formel E=mc2? Vad använder man den till? (Erik D)
/Niklas N, Äppelviken, Bromma 2004-02-17
Svar:
Jag har tagit mig friheten att slå ihop frågorna från Äppelviksskolan.
Det är svåra frågor ni ställer eftersom ni vill veta det historiska perspektivet. Det är en hel vetenskap som heter vetenskapshistoria, och det är vi inte experter på. Jag skall emellertid försöka mig på ett par kommentarer.
Relativitetsteorin publicerades av Einstein 1905. Här är originalversionen: Zur Elektrodynamik bewegter Körper . Artikeln är svårbegriplig för en modern fysiker, eftersom beteckningarna i formlerna är lite gammalmodiga och så är artikeln på tyska.
. Artikeln är svårbegriplig för en modern fysiker, eftersom beteckningarna i formlerna är lite gammalmodiga och så är artikeln på tyska.
Vid den tiden var emellertid tyska mer vetenskapens språk än engelska, och tidens fysiker hade inga större problem att förstå artikeln.
Relativitetsteorin bygger i stort på ett antagande:
att ljushastigheten c i vakuum är konstant oberoende av hur man rör sig i förhållande till ljusstrålen. Antagandet bygger på ett experiment som utfördes av Michelson-Morley 1887: History of Special Relativity . Ovanstående artikel är mycket bra, och bör ha övertygat många fysiker. Artikeln innehåller nästan hela var vi kallar den Speciella relativitetsteorin utom det ni frågar om, E=mc2. Denna härleddes i en artikel publicerad senare under 1905: Does the Inertia of a Body Depend upon Its Energy-Content
. Ovanstående artikel är mycket bra, och bör ha övertygat många fysiker. Artikeln innehåller nästan hela var vi kallar den Speciella relativitetsteorin utom det ni frågar om, E=mc2. Denna härleddes i en artikel publicerad senare under 1905: Does the Inertia of a Body Depend upon Its Energy-Content . Även denna artikel är svårläst i dag (trots att den här är översatt till engelska). I artikeln finns en länk till en engelsk översättning av Einsteins första artikel om relativitetsteorin (Zur Elektrodynamik bewegter Körper).
. Även denna artikel är svårläst i dag (trots att den här är översatt till engelska). I artikeln finns en länk till en engelsk översättning av Einsteins första artikel om relativitetsteorin (Zur Elektrodynamik bewegter Körper).
Länk 1 nedan är Einstein själv som förklarar vad formeln innebär. Här är en artikel som ger ett par olika härledningar: Year of Physics 2005 .
.
Exakta mätningar som bekräftade relativitetsteorin kom betydligt senare. Inte ens nobelkommittén var imponerad: nobelpriset Einstein fick 1921 var för hans förklaring av den fotoelektriska effekten (också 1905) och inte relativitetsteorin!
Tolkning: EkvationenE=mc2 skall tolkas så att massa och energi är ekvivalenta (utbytbara mot varandra) med "växlingskursen" c2. Eftersom c är ganska stort motsvarar även en liten massa (eller mass-skillnad) en mycket stor energi.
Bekräftelsen på E=mc2 kom först på 20/30-talet när man kunde mäta atommassor med hög precision, se fråga [12726].
Det finns många böcker om relativitetsteorin och en bra artikel i Nationalencyklopedin . Wikipedia-artiklarna
. Wikipedia-artiklarna Einstein och Special_relativity är också mycket bra.
Se även fråga [20460].
Jag har tagit mig friheten att slå ihop frågorna från Äppelviksskolan.
Det är svåra frågor ni ställer eftersom ni vill veta det historiska perspektivet. Det är en hel vetenskap som heter vetenskapshistoria, och det är vi inte experter på. Jag skall emellertid försöka mig på ett par kommentarer.
Relativitetsteorin publicerades av Einstein 1905. Här är originalversionen: Zur Elektrodynamik bewegter Körper
Vid den tiden var emellertid tyska mer vetenskapens språk än engelska, och tidens fysiker hade inga större problem att förstå artikeln.
Relativitetsteorin bygger i stort på ett antagande:
att ljushastigheten c i vakuum är konstant oberoende av hur man rör sig i förhållande till ljusstrålen. Antagandet bygger på ett experiment som utfördes av Michelson-Morley 1887: History of Special Relativity
Länk 1 nedan är Einstein själv som förklarar vad formeln innebär. Här är en artikel som ger ett par olika härledningar: Year of Physics 2005
Exakta mätningar som bekräftade relativitetsteorin kom betydligt senare. Inte ens nobelkommittén var imponerad: nobelpriset Einstein fick 1921 var för hans förklaring av den fotoelektriska effekten (också 1905) och inte relativitetsteorin!
Tolkning: Ekvationen
Bekräftelsen på E=mc2 kom först på 20/30-talet när man kunde mäta atommassor med hög precision, se fråga [12726].
Det finns många böcker om relativitetsteorin och en bra artikel i Nationalencyklopedin
Se även fråga [20460].

Vad finns det för bevis för relativitetsteorin?
Fråga:
När kunde man eller kan man fortfarande inte fastställa relativitets teorin? Vilka olika upptäckter och bevis var man tvungna att få fram?
/Frida S, Kullagymnasiet, Höganäs 2006-04-28
När kunde man eller kan man fortfarande inte fastställa relativitets teorin? Vilka olika upptäckter och bevis var man tvungna att få fram?
/Frida S, Kullagymnasiet, Höganäs 2006-04-28
Svar:
Frida! Som fysikaliskt teori måste relativitetsteorin anses mycket etablerad. Detta gäller båderelativitetsteorin, speciella
ochrelativitetsteorin, allmänna . Se
Special_theory_of_relativityConsequences_derived_from_the_Lorentz_transformation och
General_theory_of_relativityConsequences_of_Einstein's_theory
för några experimentella resultat som stöder den speciella och den allmänna relativitetsteorin.
Det universiella navigeringssystemet GPS (seGlobal_Positioning_System och nedanstående figur från Wikimedia Commons) med 24 satelliter i bana runt jorden på en höjd av 20000 km skulle helt enkelt inte fungera om man inte tog hänsyn till relativitetsteorierna.
Dels orsakar banrörelsen att den mycket exakta klockan i en satellit saktar sig 7 mikrosekunder per dygn pga den speciella relativitetsteorin. Eftersom satelliten befinner sig i ett svagare gravitationsfält går klockan 45 mikrosekunder per dygn snabbare. Nettokorrektionen 45-7=38 mikrosekunder per dygn appliceras genom att man justerar klockan att gå lite långsammare innan satelliten skickas upp. Man synkroniserar även alla klockorna med hjälp av klockor på marken. Se vidare länk 1.
Se vidareSpecial_relativity och General_relativity .
Tillägg 5/4/2011:
Uppskattning av effekterna
Konstanter:
Ljushastigheten: c = 3.00108 m/s
Gravitationskonstanten: G = 6.67510-11m3/(kg.s2)
Jordens massa: M = 5.9741024 kg
Jordens radie: R = 6.37106 m
GPS-satelliternas avstånd från jordens centrum (20000 km över jordytan): RGPS = 26.37106 m
Speciell relativitet
Vi räknar från jordens centrum eftersom satelliterna går ganska högt och jordens rotationshastighet är liten (mindre än 500 m/s) jämfört med satelliternas hastighet.
Satellitens hastighet v ges av
mv2/RGPS = mMG/(RGPS)2
vilket blir
v = sqrt(MG/RGPS) = sqrt(5.9710246.6710-11/(26.367106) = 3886 m/s
Klockan påverkas med g-faktorn (Special_relativityTime_dilation_and_length_contraction )
g = sqrt(1-(v/c)2) =
sqrt(1-(3886/300000000)^2) = 0.9999999999161055
Den relativa korrektionen blir
1 - g = 8.38910-11
och korrektionen på ett dygn blir
8.38910-11606024 = 7.2510-6 s
eller c:a 7 mikrosekunder.
Allmän relativitet
Denna korrektion har att göra med att man måste bevara totala energin även i ett gravitationsfält, se fråga [16989], stycket gravitationell rödförskjutning. För att bevara energiprincipen måste tiden i ett starkt gravitationsfält gå långsammare än i ett svagare. Tiden går alltså till synes snabbare i GPS satelliterna än på jordytan. Den relativa korrektionen ges av potentialskillnaden dividerat med viloenergin mc2 (m är satellitens massa som kommer att försvinna i slututtrycket).
Om gravitationspotentialen är U(r) så gäller genom integration av gravitationskraften
U(r) = -mMG/r
Ändringen i potentiell energi om vi går från jordytan till satellitbanan blir
DU = -mMG/RGPS -(-mMG/R) = -mMG(1/RGPS -1/R)
Med insatta värden blir
DU = m4.714 107
Om vi dividerar detta med viloenergin mc2 får vi den relativa korrektionen till
5.237 10-10
På ett dygn blir korrektionen
5.237 10-10246060 s = 45.2 mikrosekunder
vilket stämmer bra med värdet ovan.
Frida! Som fysikaliskt teori måste relativitetsteorin anses mycket etablerad. Detta gäller både
och
för några experimentella resultat som stöder den speciella och den allmänna relativitetsteorin.
Det universiella navigeringssystemet GPS (se
Dels orsakar banrörelsen att den mycket exakta klockan i en satellit saktar sig 7 mikrosekunder per dygn pga den speciella relativitetsteorin. Eftersom satelliten befinner sig i ett svagare gravitationsfält går klockan 45 mikrosekunder per dygn snabbare. Nettokorrektionen 45-7=38 mikrosekunder per dygn appliceras genom att man justerar klockan att gå lite långsammare innan satelliten skickas upp. Man synkroniserar även alla klockorna med hjälp av klockor på marken. Se vidare länk 1.
Se vidare
Tillägg 5/4/2011:
Uppskattning av effekterna
Konstanter:
Ljushastigheten: c = 3.00108 m/s
Gravitationskonstanten: G = 6.67510-11m3/(kg.s2)
Jordens massa: M = 5.9741024 kg
Jordens radie: R = 6.37106 m
GPS-satelliternas avstånd från jordens centrum (20000 km över jordytan): RGPS = 26.37106 m
Speciell relativitet
Vi räknar från jordens centrum eftersom satelliterna går ganska högt och jordens rotationshastighet är liten (mindre än 500 m/s) jämfört med satelliternas hastighet.
Satellitens hastighet v ges av
mv2/RGPS = mMG/(RGPS)2
vilket blir
v = sqrt(MG/RGPS) = sqrt(5.9710246.6710-11/(26.367106) = 3886 m/s
Klockan påverkas med g-faktorn (
g = sqrt(1-(v/c)2) =
sqrt(1-(3886/300000000)^2) = 0.9999999999161055
Den relativa korrektionen blir
1 - g = 8.38910-11
och korrektionen på ett dygn blir
8.38910-11606024 = 7.2510-6 s
eller c:a 7 mikrosekunder.
Allmän relativitet
Denna korrektion har att göra med att man måste bevara totala energin även i ett gravitationsfält, se fråga [16989], stycket gravitationell rödförskjutning. För att bevara energiprincipen måste tiden i ett starkt gravitationsfält gå långsammare än i ett svagare. Tiden går alltså till synes snabbare i GPS satelliterna än på jordytan. Den relativa korrektionen ges av potentialskillnaden dividerat med viloenergin mc2 (m är satellitens massa som kommer att försvinna i slututtrycket).
Om gravitationspotentialen är U(r) så gäller genom integration av gravitationskraften
U(r) = -mMG/r
Ändringen i potentiell energi om vi går från jordytan till satellitbanan blir
DU = -mMG/RGPS -(-mMG/R) = -mMG(1/RGPS -1/R)
Med insatta värden blir
DU = m4.714 107
Om vi dividerar detta med viloenergin mc2 får vi den relativa korrektionen till
5.237 10-10
På ett dygn blir korrektionen
5.237 10-10246060 s = 45.2 mikrosekunder
vilket stämmer bra med värdet ovan.

Varför ramlar inte elektronerna in i kärnan?
Fråga:
Hej! Vi känner alla till den vanliga atommodellen, med en kärna i mitten och elektroner som snurrar runt den. Men den förklarar inte flera saker som, t.ex, varför fäster sig inte elektronerna direkt på kärnan? Så jag undrar om det finns någon bättre modell över atomen som förklarar mitt exempel.
Tack!
/Oskar H, Cybergymnasiet, Malmö 2010-05-17
Hej! Vi känner alla till den vanliga atommodellen, med en kärna i mitten och elektroner som snurrar runt den. Men den förklarar inte flera saker som, t.ex, varför fäster sig inte elektronerna direkt på kärnan? Så jag undrar om det finns någon bättre modell över atomen som förklarar mitt exempel.
Tack!
/Oskar H, Cybergymnasiet, Malmö 2010-05-17
Svar:
Oskar! Modellen som beskrivs i fråga [13733] - elektronfördelningen är som ett suddigt moln - är mer realistisk. Elektroner kan pgaHeisenbergs obestämdhetsrelation inte stängas in i kärnan. Innan man upptäckte neutronen (1932) trodde man att atomkärnorna innehöll elektroner för att ge rätt kärnladdning. Det visade sig emellertid att obestämdhetsrelationen gjorde att elektroners rörelse inte kan begränsas till kärnan. När man upptäckt neutronen och förstått att en kärna består av Z protoner och N neutroner (där A=Z+N är masstalet) så var problemet löst: det krävdes inga elektroner i kärnan så de fick hålla sig på mycket större avstånd.
Oskar kom tillbaka med följande fråga:
Jag har försökt bli klok på varför man inte kan bestämma elektroners exakta position och varför de inte kan befinna sig i atomkärnan enligt Heisenbergs obestämdhetsrelation, men jag begriper mig inte på den. Kan ni förtydliga vad det egentligen obestämdhetsprincipen säger?
Oscar! Det var det konventionella svaret du fick, och jag håller med att jag kunde varit lite tydligare. Så låt oss först räkna lite.
Obestämdhetsrelationen ges av (Heisenberg_uncertainty_principle ):
DxDpx = h/4p (1)
Om vi stänger in en elektron i en atomkärna så är Dx ungefär 10-15 m. Vi får då
Dp = 0.510-34/10-15 Js/m = 0.510-19 Ns
För att få en bättre uppfattning om vad detta betyder gör vi om rörelsemängd p till energi E. Det relativistiska sambandet är (vi måste använda relativistiska samband eftersom hastigheten är hög)
E2 = (pc)2 + (mc2)2 (2)
Eftersom energin kommer att visa sig vara mycket hög så kan vi försumma elektronens viloenergi mc2 och får det enkla sambandet
E = pc (3)
(Detta är för övrigt även sambandet mellan energi och rörelsemängd för en foton.) Vi får
E = 0.510-193108 Nsm/s = 1.510-11 J = 1.510-11/(1.60210-13) MeV = 100 MeV.
För det första kan vi konstatera att det var OK att försumma vilomassan för elektronen (0.511 MeV). För det andra ser vi att detta är en mycket hög energi och vi känner ingen kraft som är stark nog att hålla elektronen fångad. Coulombkraften räcker inte till på långa vägar - den ger det lägsta tillståndet (1s) i en atom på medelavståndet 10-10 m, vilket är fem storleksordningar större än atomkärnans utsträckning.
Små system som atomer och kärnor följer alltså inte de lagar vi är vana vid i vardagen. Två olika laddade klot attraherar varandra och kommer att fastna vid varandra. Elektroner följer emellertid kvantmekanikens lagar och måste bland annat lyda Heisenbergs obestämdhetsrelation.
Det är emellertid inte helt lätt att tolka vad kvantmekaniken säger oss om naturen. Se t.ex. KvantmekanikExempel_p.C3.A5_tolkningar .
.
De flesta fysiker föredrar Köpenhamnstolkningen. Den sista, lite skämtsamma, "håll käft och räkna!" är inte heller så dum. Även om kvantmekaniken är svårförståelig så stämmer resultatet mycket bra med observationerna, och det är det viktigaste för en fysikalisk teori.
Länkarna 1 och 2 är svar på liknande frågor.
Man kan även resonera på ett annat sätt: om man stänger in elektronen i en låda om 210-15 m så måste våglängden vara högst 410-15 m (vågen måste ha en nod där potentialen blir oändlig). Vi får rörelsemängden
p = h/l = 6.6 10-34/4 10-15 = 2 10-19 Ns
vilket är av samma storleksordning som ovan.
/Peter E 2010-05-23
Oskar! Modellen som beskrivs i fråga [13733] - elektronfördelningen är som ett suddigt moln - är mer realistisk. Elektroner kan pga
Oskar kom tillbaka med följande fråga:
Jag har försökt bli klok på varför man inte kan bestämma elektroners exakta position och varför de inte kan befinna sig i atomkärnan enligt Heisenbergs obestämdhetsrelation, men jag begriper mig inte på den. Kan ni förtydliga vad det egentligen obestämdhetsprincipen säger?
Oscar! Det var det konventionella svaret du fick, och jag håller med att jag kunde varit lite tydligare. Så låt oss först räkna lite.
Obestämdhetsrelationen ges av (
DxDpx = h/4p (1)
Om vi stänger in en elektron i en atomkärna så är Dx ungefär 10-15 m. Vi får då
Dp = 0.510-34/10-15 Js/m = 0.510-19 Ns
För att få en bättre uppfattning om vad detta betyder gör vi om rörelsemängd p till energi E. Det relativistiska sambandet är (vi måste använda relativistiska samband eftersom hastigheten är hög)
E2 = (pc)2 + (mc2)2 (2)
Eftersom energin kommer att visa sig vara mycket hög så kan vi försumma elektronens viloenergi mc2 och får det enkla sambandet
E = pc (3)
(Detta är för övrigt även sambandet mellan energi och rörelsemängd för en foton.) Vi får
E = 0.510-193108 Nsm/s = 1.510-11 J = 1.510-11/(1.60210-13) MeV = 100 MeV.
För det första kan vi konstatera att det var OK att försumma vilomassan för elektronen (0.511 MeV). För det andra ser vi att detta är en mycket hög energi och vi känner ingen kraft som är stark nog att hålla elektronen fångad. Coulombkraften räcker inte till på långa vägar - den ger det lägsta tillståndet (1s) i en atom på medelavståndet 10-10 m, vilket är fem storleksordningar större än atomkärnans utsträckning.
Små system som atomer och kärnor följer alltså inte de lagar vi är vana vid i vardagen. Två olika laddade klot attraherar varandra och kommer att fastna vid varandra. Elektroner följer emellertid kvantmekanikens lagar och måste bland annat lyda Heisenbergs obestämdhetsrelation.
Det är emellertid inte helt lätt att tolka vad kvantmekaniken säger oss om naturen. Se t.ex. KvantmekanikExempel_p.C3.A5_tolkningar
 .
.De flesta fysiker föredrar Köpenhamnstolkningen. Den sista, lite skämtsamma, "håll käft och räkna!" är inte heller så dum. Även om kvantmekaniken är svårförståelig så stämmer resultatet mycket bra med observationerna, och det är det viktigaste för en fysikalisk teori.
Länkarna 1 och 2 är svar på liknande frågor.
Man kan även resonera på ett annat sätt: om man stänger in elektronen i en låda om 210-15 m så måste våglängden vara högst 410-15 m (vågen måste ha en nod där potentialen blir oändlig). Vi får rörelsemängden
p = h/l = 6.6 10-34/4 10-15 = 2 10-19 Ns
vilket är av samma storleksordning som ovan.
/Peter E 2010-05-23
Är det verkligen en relativistisk effekt att ett blybatteri har en spänning på 2V och inte 0.3V?
Fråga:
Hej!
I dagens tidning, UNT, nämns att elektronerna i en blyatom i ett bilbatteri måste hålla så hög fart för att inte dras in i kärnan att elektronmassan ökar relativistiskt, och det rätt mycket, och att detta medförde att energiutbytet kan vara så stort som det är.
Fråga: Är det en vanlig kinetisk energi hos elektroner som bidrar till den elektriska? Och hur sker d e t?
/Thomas �, Knivsta 2011-01-27
Hej!
I dagens tidning, UNT, nämns att elektronerna i en blyatom i ett bilbatteri måste hålla så hög fart för att inte dras in i kärnan att elektronmassan ökar relativistiskt, och det rätt mycket, och att detta medförde att energiutbytet kan vara så stort som det är.
Fråga: Är det en vanlig kinetisk energi hos elektroner som bidrar till den elektriska? Och hur sker d e t?
/Thomas �, Knivsta 2011-01-27
Svar:
Hej Thomas! Du syftar på artikeln under länk 1. Att man behöver relativistiska korrektioner vid beräkningar av atomära nivåer är inget nytt. Detta gäller särskilt de innersta skalen. Det är däremot lite förvånande att relativitetskorrektionerna har så stor påverkan på elektriska egenskaper som ju styrs av de yttre skalen. Mer om detta nedan.
Som alltid vill jag emellertid varna för modellen att elektronerna är små laddade kulor som snurrar i banor kring kärnan och riskerar falla ner i densamma, se fråga [13733] och [17237]. Verkligheten är såpass annorlunda de bilder vi kan föreställa oss eftersom vår erfarenhet kommer från den makroskopiska världen där partiklar och vågor uppför sig "normalt".
För att "förstå" atomära system löser man en ekvation, schrödingerekvationen (SE), seSchrödinger_equation . För atomer som är mer komplexa än väteatomen är det inte trivialt att lösa SE och man tvingas till approximationer och omfattande iterativa processer.
SE tar inte hänsyn till relativistiska effekter, t.ex. att en elektrons massa beror av dess hastighet (speciella relativitetsteorin). Diracekvationen (Dirac_equation ) gör emellertid detta. Problemet är att den är ännu mer svårhanterlig.
Artikeln från Uppsala universitet (länk 2 är en light-version, originalartikeln är bitvis rätt svår att förstå för icke-specialister) redovisar en beräkning av energinivåerna i bly både icke-relativistiskt och relativistiskt. Man kan med den relativistiska lösningen mycket bra reproducera EMS (fråga [17476]) för ett blybatteri. Den icke-relativistiska lösningen avviker emellertid väsentligt från de c:a 2V man observerar.
För tenn (som ligger ovanför bly i det periodiska systemet och borde likna bly) är den relativistiska effekten mycket mindre, vilket medför att tennbatterier är ganska värdelösa eftersom EMS är mycket liten. Anledningen är att tenn har betydligt lägre kärnladdning än bly (50 respektive 82), vilket innebär att elektronerna rör sig långsammare i tenn.
Det visar sig från räkningarna att det är framför allt 6s nivåerna (6s är bland valens-nivåerna i bly) som påverkas av relativistiska effekter. Eftersom s motsvarar rörelsemängdsmomentet 0 har dessa elektroner en liten men dock sannolikhet att befinna sig nära atomkärnan. På grund av blys höga kärnladdning rör de sig då mycket snabbt, och relativistiska effekter blir stora. Ökningen i elektronens massa gör att orbitalen krymper och fördelningen hos elektronmolnet förskjuts in mot kärnan.
Sammanfattningsvis beror effekten på att relativistiska effekter för elektroner nära blykärnan påverkar valensnivåerna, vilka i sin tur bestämmer EMS för blybatteriet.
Jag tycker artikeln är intressant av flera skäl:
Den relativistiska kontraktionen av 6s orbitalen förklarar även varför guld glimmar gult och varför guld är så lite reaktivt: What Gives Gold that Mellow Glow? . Se fråga [14685] för fler experimentella stöd för den speciella och allmänna relatiovitetsteorin.
. Se fråga [14685] för fler experimentella stöd för den speciella och allmänna relatiovitetsteorin.
Slutligen kan jag inte låta bli att citera den avslutande meningen i artikeln: Finally, we note that cars start due to relativity :-).
/Peter E 2011-01-27
Hej Thomas! Du syftar på artikeln under länk 1. Att man behöver relativistiska korrektioner vid beräkningar av atomära nivåer är inget nytt. Detta gäller särskilt de innersta skalen. Det är däremot lite förvånande att relativitetskorrektionerna har så stor påverkan på elektriska egenskaper som ju styrs av de yttre skalen. Mer om detta nedan.
Som alltid vill jag emellertid varna för modellen att elektronerna är små laddade kulor som snurrar i banor kring kärnan och riskerar falla ner i densamma, se fråga [13733] och [17237]. Verkligheten är såpass annorlunda de bilder vi kan föreställa oss eftersom vår erfarenhet kommer från den makroskopiska världen där partiklar och vågor uppför sig "normalt".
För att "förstå" atomära system löser man en ekvation, schrödingerekvationen (SE), se
SE tar inte hänsyn till relativistiska effekter, t.ex. att en elektrons massa beror av dess hastighet (speciella relativitetsteorin). Diracekvationen (
Artikeln från Uppsala universitet (länk 2 är en light-version, originalartikeln är bitvis rätt svår att förstå för icke-specialister) redovisar en beräkning av energinivåerna i bly både icke-relativistiskt och relativistiskt. Man kan med den relativistiska lösningen mycket bra reproducera EMS (fråga [17476]) för ett blybatteri. Den icke-relativistiska lösningen avviker emellertid väsentligt från de c:a 2V man observerar.
För tenn (som ligger ovanför bly i det periodiska systemet och borde likna bly) är den relativistiska effekten mycket mindre, vilket medför att tennbatterier är ganska värdelösa eftersom EMS är mycket liten. Anledningen är att tenn har betydligt lägre kärnladdning än bly (50 respektive 82), vilket innebär att elektronerna rör sig långsammare i tenn.
Det visar sig från räkningarna att det är framför allt 6s nivåerna (6s är bland valens-nivåerna i bly) som påverkas av relativistiska effekter. Eftersom s motsvarar rörelsemängdsmomentet 0 har dessa elektroner en liten men dock sannolikhet att befinna sig nära atomkärnan. På grund av blys höga kärnladdning rör de sig då mycket snabbt, och relativistiska effekter blir stora. Ökningen i elektronens massa gör att orbitalen krymper och fördelningen hos elektronmolnet förskjuts in mot kärnan.
Sammanfattningsvis beror effekten på att relativistiska effekter för elektroner nära blykärnan påverkar valensnivåerna, vilka i sin tur bestämmer EMS för blybatteriet.
Jag tycker artikeln är intressant av flera skäl:
- Att man med grundläggande kvantmekanik kan beräkna makroskopiska storheter.
- Relativistiska effekter är inte alltid små och knappt mätbara korrektioner.
- Att man kan räkna på molekyler och joner.
Den relativistiska kontraktionen av 6s orbitalen förklarar även varför guld glimmar gult och varför guld är så lite reaktivt: What Gives Gold that Mellow Glow?
Slutligen kan jag inte låta bli att citera den avslutande meningen i artikeln: Finally, we note that cars start due to relativity :-).
/Peter E 2011-01-27
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.
Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar

