Vill du ha ett snabbt svar - sök i databasen
Nyckelord: fysik
79 träffar
Varför känns utandningsluften varmare om man andas ut med vidöppen mun jämfört med mer stängd mun?
Fråga:
En av mina elever undrade varför utandningsluften känns varmare om man andas ut med vidöppen mun jämfört med mer stängd mun. Jag har själv provat och det stämmer nog men varför? Beror det på om luften kommer nere från lungorna eller från munnen?
/Marianne L, Frostaskolan, Hörby 2009-10-22
En av mina elever undrade varför utandningsluften känns varmare om man andas ut med vidöppen mun jämfört med mer stängd mun. Jag har själv provat och det stämmer nog men varför? Beror det på om luften kommer nere från lungorna eller från munnen?
/Marianne L, Frostaskolan, Hörby 2009-10-22
Svar:
Marianne! Nej, luften kommer i båda fallen både från munnen och lungorna. Skillnaden är att om du stänger munnen och bara lämnar ett litet hål, så skapas ett litet övertryck i munnen. Eftersom det är ett lite lägre tryck utanför munnen, måste den utströmmande luften expandera. Om en gas får expandera fritt så kyls den. Tvärtom, om en gas komprimeras så värms den upp. Du har säkert märkt att cykelpumpen blir varm när du pumpar upp däcket.
/Peter E 2009-10-22
Marianne! Nej, luften kommer i båda fallen både från munnen och lungorna. Skillnaden är att om du stänger munnen och bara lämnar ett litet hål, så skapas ett litet övertryck i munnen. Eftersom det är ett lite lägre tryck utanför munnen, måste den utströmmande luften expandera. Om en gas får expandera fritt så kyls den. Tvärtom, om en gas komprimeras så värms den upp. Du har säkert märkt att cykelpumpen blir varm när du pumpar upp däcket.
/Peter E 2009-10-22
Berg-och-dal bana med loop
Fråga:
Frågan gäller en berg-och-dal bana med en loop.
Hur stor är centripetalaccelerationen längst upp på karusellen? Var är centripetalaccelerationen som störst?
/Ali z, BORGARSKOLAN, MALMÖ 2009-11-05
Frågan gäller en berg-och-dal bana med en loop.
Hur stor är centripetalaccelerationen längst upp på karusellen? Var är centripetalaccelerationen som störst?
/Ali z, BORGARSKOLAN, MALMÖ 2009-11-05
Svar:
Ali! Jag hade lite svårt att förstå din fråga. Det du frågar om är nog en berg-och-dalbana (Roller_coaster , Roller_coaster_elements ) med en loop (Vertical_loop ), se nedanstående foto av den första loopen (Coney Island, New York) från Wikimedia Commons. Jag har kortat ner din fråga något.
Jag tänkte ta upp ett par saker av vad jag tror du frågade om: hur räknar man ut vagnens hastighet i olika punkter och hur stora är g-krafterna? Sajten Lisebergs-Fysik innehåller mycket mer information bland annat om berg-och-dal banor.
innehåller mycket mer information bland annat om berg-och-dal banor.
För att få någon idé om storlekar, hastigheter etc, så har jag tittat på data från ett typexempel, länk 1.
En klassisk berg-och-dal bana fungerar så att vagnen dras upp till maxhöjden, och får sedan rulla i princip fritt ner och upp längs spåret. En förenklad version visas i figuren nedan. Vagnen startar med hastigheten 0 från punkt 1. Den accelereras nedför backen och går runt loopen. I verkligheten är naturligtvis loopen lite skruvad så att utgången är vid sidan av ingången.
Om vi antar att det inte finns några friktionsförluster kan vi använda energiprincipen för att räkna ut hastigheten i olika punkter: Totala energin = potentiell energi + kinetisk energi, Epot + Ekin = konstant.
Vagnens massa är M kg och vi räknar med tyngdaccelerationen g=10 m/s2. Radien på loopen är r=5 m.
I tabellen nedan listas värden för punkterna 1-4. De olika kolumnerna är:
Nr Punkt nummer
h Höjd över nollnivån (lägsta nivån [punkt 2] har h=0)
Epot Potentiell energi: Mgh
Ekin = 160M - Epot
v2 räknas ut från Ekin = Mv2/2
v räknas ut från v2
v2/r är centripetalaccelerationen i cirkelbanan i m/s2
C acc är centripetalaccelerationen uttryckt i g
Totalt g är totala g-kraften om vi även tar tyngdaccelerationen i beaktande, se vektordiagrammen längst ner i figuren. I stället för att involvera krafter är det i detta fallet enklare att räkna med accelerationer. Tyngkraften motsvaras då av en acceleration riktad rakt upp med beloppet 1g (de små svarta pilarna i figuren).
Vi kan räkna ut vad starthöjden skulle vara om centripetalaccelerationen i punkt 4 skulle vara g, dvs passagerarana skulle vara tyngdlösa:
v2/r = 10 -> v2 = 105 = 50
Ekin = Mv2/2 = M50/2 = 25M
Potentiella energin 25M motsvarar höjden 2.5 m, så starthöjden behöver vara 12.5 m för att centripetalaccelerationen i punkt 4 precis skall kompensera tyngaccelerationen.
Kommentarer
1 Maximala g-kraften i detta exemplet är 7.4 (i punkt 2) medan det i länk 1 sägs att den maximala g-kraften är 4. Ett skäl till avvikelsen kan vara att loopen inte vilar på lägsta nivån eller har större radie. Ett annat skäl är att man gör inte loopen cirkulär, utan päronformad med tjocka änden nedåt. Man får då en större krökningsradie där vagnen rör sig snabbast, och en mindre radie där den rör sig långsammast. Man jämnar alltså ut g-kraftena i loopen.
2 Det kan tyckas farligt att vagnen är upp-och-ner i toppen av loopen. I moderna anläggningar (men inte i den avbildade nedan) har man dubbla skenor både över och under hjulen. Om alltså vagnen skulle tappa fart så att den inte går tillräckligt snabbt på toppen, så skulle den ändå hänga kvar i de extra skenorna.
Se även Berg-_och_dalbana .
.
Ali! Jag hade lite svårt att förstå din fråga. Det du frågar om är nog en berg-och-dalbana (
Jag tänkte ta upp ett par saker av vad jag tror du frågade om: hur räknar man ut vagnens hastighet i olika punkter och hur stora är g-krafterna? Sajten Lisebergs-Fysik
För att få någon idé om storlekar, hastigheter etc, så har jag tittat på data från ett typexempel, länk 1.
En klassisk berg-och-dal bana fungerar så att vagnen dras upp till maxhöjden, och får sedan rulla i princip fritt ner och upp längs spåret. En förenklad version visas i figuren nedan. Vagnen startar med hastigheten 0 från punkt 1. Den accelereras nedför backen och går runt loopen. I verkligheten är naturligtvis loopen lite skruvad så att utgången är vid sidan av ingången.
Om vi antar att det inte finns några friktionsförluster kan vi använda energiprincipen för att räkna ut hastigheten i olika punkter: Totala energin = potentiell energi + kinetisk energi, Epot + Ekin = konstant.
Vagnens massa är M kg och vi räknar med tyngdaccelerationen g=10 m/s2. Radien på loopen är r=5 m.
I tabellen nedan listas värden för punkterna 1-4. De olika kolumnerna är:
Nr Punkt nummer
h Höjd över nollnivån (lägsta nivån [punkt 2] har h=0)
Epot Potentiell energi: Mgh
Ekin = 160M - Epot
v2 räknas ut från Ekin = Mv2/2
v räknas ut från v2
v2/r är centripetalaccelerationen i cirkelbanan i m/s2
C acc är centripetalaccelerationen uttryckt i g
Totalt g är totala g-kraften om vi även tar tyngdaccelerationen i beaktande, se vektordiagrammen längst ner i figuren. I stället för att involvera krafter är det i detta fallet enklare att räkna med accelerationer. Tyngkraften motsvaras då av en acceleration riktad rakt upp med beloppet 1g (de små svarta pilarna i figuren).
Nr h Epot Ekin v2 v v2/r C acc Totalt g
1 16 160M 0 0 0
2 0 0 160M 320 18 64 6.4 7.4
3 5 50M 110M 220 15 44 4.4 4.5
4 10 100M 60M 120 11 24 2.4 1.4
m J J (m/s)2 m/s m/s2
Vi kan räkna ut vad starthöjden skulle vara om centripetalaccelerationen i punkt 4 skulle vara g, dvs passagerarana skulle vara tyngdlösa:
v2/r = 10 -> v2 = 105 = 50
Ekin = Mv2/2 = M50/2 = 25M
Potentiella energin 25M motsvarar höjden 2.5 m, så starthöjden behöver vara 12.5 m för att centripetalaccelerationen i punkt 4 precis skall kompensera tyngaccelerationen.
Kommentarer
1 Maximala g-kraften i detta exemplet är 7.4 (i punkt 2) medan det i länk 1 sägs att den maximala g-kraften är 4. Ett skäl till avvikelsen kan vara att loopen inte vilar på lägsta nivån eller har större radie. Ett annat skäl är att man gör inte loopen cirkulär, utan päronformad med tjocka änden nedåt. Man får då en större krökningsradie där vagnen rör sig snabbast, och en mindre radie där den rör sig långsammast. Man jämnar alltså ut g-kraftena i loopen.
2 Det kan tyckas farligt att vagnen är upp-och-ner i toppen av loopen. I moderna anläggningar (men inte i den avbildade nedan) har man dubbla skenor både över och under hjulen. Om alltså vagnen skulle tappa fart så att den inte går tillräckligt snabbt på toppen, så skulle den ändå hänga kvar i de extra skenorna.
Se även Berg-_och_dalbana
 .
.
Länkar: http://www.rcdb.com/181.htm
/Peter E 2009-11-06
Test av mikrovågsugn
Fråga:
Jag har fått höra att man i framförallt USA testar mikrovågsugnar regelbundet (någon gång per år) för att se om de börjat läcka mikrovågor. Detta görs hemma genom att man kan hålla ett lysrör i närheten av mikron, lyser det så är ugnen för gammal och ska kasseras. Ligger någon som helst sanning i detta, att mikron kan bli gammal och börja läcka?
/Annika L, Lund 2010-02-05
Jag har fått höra att man i framförallt USA testar mikrovågsugnar regelbundet (någon gång per år) för att se om de börjat läcka mikrovågor. Detta görs hemma genom att man kan hålla ett lysrör i närheten av mikron, lyser det så är ugnen för gammal och ska kasseras. Ligger någon som helst sanning i detta, att mikron kan bli gammal och börja läcka?
/Annika L, Lund 2010-02-05
Svar:
Annika! Jag tror du blivit utsatt för ett skämt! Om det finns så mycket mikrovågor utanför ugnen att ett lysrör tänds, så är det mycket illa!
Mikovågorna hålls innne i ugnen genom att den är konstruerad som en faradaybur (se fråga [8879])
- solid metallplåt inne i ugnen och ett finmaskigt metallnät på luckan. Maskorna är betydligt mindre än mikrovågornas våglängd, så dessa kan inte slippa ut. Enda möjligheten är att dörren eller nätet skadats, men det kan man lätt se. Man behöver alltså inte testa om ungen läcker mikrovågor. Om man vill mäta strålningen (t.ex. för att testa en ny konstruktion) bör man ha mycket bättre mätapparatur än ett lysrör.
Se fråga [16041] om vad som händer med mikrovågsugnar när de blir gamla. Se mer om mikrovågsugnar:mikrovågsugn , länk 1 från strålsäkerhetsmyndigheten och länk 2.
Se fråga [3969] om hur effektiv faradayburen i en mikrovågsugn är.
Hur man kontrollerar effekten hos en mikrovågsugn
När mikrovågsugnen blir gammal blir magnetronen som genererar mikrovågorna mindre effektiv, och det tar längre tid att värma maten. Så här kan du kontrollera hur effektiv din mikrovågsugn är. Du behöver bara en skål (glas eller keramik) med 1 liter kallt vatten och en hyggligt exakt termometer.
Mät temperaturen på vattnet. Säg att vattnet är 20oC. Kör ugnen 1 minut. Mät vattentemperaturen igen. Säg att vattnet nu är 30oC. Sedan får vi räkna lite för att få fram effekten. Energin som krävs för att värma vattnet DT K är:
W = mcDT
där m är massan och c är vattnets specifika värmekapacitet 4180 J/(kg K).
Om vi kör mikron under tiden t får vi effekten
P = W/t = mcDT/t
1 liter vatten väger 1 kg, så effekten blir
P = 4180DT/t
Om vi körde mikron 1 minut och temperaturskillnaden var 10 K (eftersom vi har att göra med temperaturskillnader kan vi använda Celsius eller Kelvin) blir effekten
P = 418010/60 = 697 W
Om temperaturdifferensen blir liten bör man öka tiden t för att få bättre noggrannhet.
Den uppmätta effekten jämförs sedan med den nominella effekten enligt bruksanvisningen. Man kan även mäta in-effekten direkt med en wattmeter (seWatt_meter , bilden nedan). Om effekten är betydligt lägre än vad den skall vara är mikrovågsugnen skadad.
Om ovanstående är för krångligt kan man om man har en "standardportion", t.ex. ett fruset halvt franskbröd, helt enkelt se om upptiningen tar längre tid än vanligt.
Annika! Jag tror du blivit utsatt för ett skämt! Om det finns så mycket mikrovågor utanför ugnen att ett lysrör tänds, så är det mycket illa!
Mikovågorna hålls innne i ugnen genom att den är konstruerad som en faradaybur (se fråga [8879])
- solid metallplåt inne i ugnen och ett finmaskigt metallnät på luckan. Maskorna är betydligt mindre än mikrovågornas våglängd, så dessa kan inte slippa ut. Enda möjligheten är att dörren eller nätet skadats, men det kan man lätt se. Man behöver alltså inte testa om ungen läcker mikrovågor. Om man vill mäta strålningen (t.ex. för att testa en ny konstruktion) bör man ha mycket bättre mätapparatur än ett lysrör.
Se fråga [16041] om vad som händer med mikrovågsugnar när de blir gamla. Se mer om mikrovågsugnar:
Se fråga [3969] om hur effektiv faradayburen i en mikrovågsugn är.
Hur man kontrollerar effekten hos en mikrovågsugn
När mikrovågsugnen blir gammal blir magnetronen som genererar mikrovågorna mindre effektiv, och det tar längre tid att värma maten. Så här kan du kontrollera hur effektiv din mikrovågsugn är. Du behöver bara en skål (glas eller keramik) med 1 liter kallt vatten och en hyggligt exakt termometer.
Mät temperaturen på vattnet. Säg att vattnet är 20oC. Kör ugnen 1 minut. Mät vattentemperaturen igen. Säg att vattnet nu är 30oC. Sedan får vi räkna lite för att få fram effekten. Energin som krävs för att värma vattnet DT K är:
W = mcDT
där m är massan och c är vattnets specifika värmekapacitet 4180 J/(kg K).
Om vi kör mikron under tiden t får vi effekten
P = W/t = mcDT/t
1 liter vatten väger 1 kg, så effekten blir
P = 4180DT/t
Om vi körde mikron 1 minut och temperaturskillnaden var 10 K (eftersom vi har att göra med temperaturskillnader kan vi använda Celsius eller Kelvin) blir effekten
P = 418010/60 = 697 W
Om temperaturdifferensen blir liten bör man öka tiden t för att få bättre noggrannhet.
Den uppmätta effekten jämförs sedan med den nominella effekten enligt bruksanvisningen. Man kan även mäta in-effekten direkt med en wattmeter (se
Om ovanstående är för krångligt kan man om man har en "standardportion", t.ex. ett fruset halvt franskbröd, helt enkelt se om upptiningen tar längre tid än vanligt.

Hur har man kommit fram till att fotonens energi är W=hf?
Fråga:
Hej!
hur har man kommit fram till att fotonens energi är W=hf, där h är planks konstant och f är frekvensen? finns det en svensk länk där man kan läsa om det i djupet tack!!
/Ali Z, malmö borgarskolan, malmö 2010-02-23
Hej!
hur har man kommit fram till att fotonens energi är W=hf, där h är planks konstant och f är frekvensen? finns det en svensk länk där man kan läsa om det i djupet tack!!
/Ali Z, malmö borgarskolan, malmö 2010-02-23
Svar:
Hej Ali! Bra fråga! Formeln för fotonens energi
E = hv (av konvention använder man oftast v [grekiska ny] för fotonens frekvens)
är ju så djupt rotad i den moderna fysiken att man kanske glömmer vad den kommer ifrån.
När det gäller fysikaliska samband uppkommer de typiskt på ett av två sätt:
1 ett experimentellt uppmätt samband eller lag
2 ett antagande som leder till andra samband som kan verifieras experimentellt
eller en kombination av 1 och 2
När det gäller fotonens energi är det till att börja med fall 2: Max Planck (Max_Planck ) gjorde antagandet att energin var proportionell mot frevensen för att härleda ett fungerande uttryck för den den experimentellt observerade fördelningen hos temperaturstrålning (1900), se Plancks strålningslag , speciellt fråga [12397] och Planck's_law (den senare på engelska).
Bilden nedan från Wikimedia CommonsUltraviolet_catastrophe ) visar uppmätt temperaturstålning för tre olika temperaturer (nedre kurvorna). Den övre, svarta kurvan visar den klassiska förutsägelsen (Rayleigh–Jeans law). Som synes avviker den senare mycket från den observerade fördelningen, speciellt för korta våglängder.
Plancks uttryck representerade uppmätta data mycket bra även för korta våglängder. Plancks antagande att energin var given av strålningens frekvens var en avvikelse från den klassiska teorin där energin gavs av amplituden hos strålningen. Utan att veta det förebådade Planck den kommande kvantmekaniken.
Einstein var i sin artikel om fotoelektriska effekten (1905) mycket tydlig med kvantiseringen, och införde begreppet foton för en "ljus-partikel". I fråga [2931] visas data för fotoelektriska effekten som visar proportionaliteten mellan energi och frekvens.
Det mest direkta beviset kom genom Bohrs atommodell (1913). Man kunde bygga upp energidiagram där skillnaden i energin mellan två tillstånd var lika med energin hos fotonen som utsändes vid en övergång. Man kunde mäta våglängden och med hjälp av det generella sambandet mellan vågens utbredningshastighet c, våglängden l och frekvensen v
c = lv
verifiera proportionaliteten mellan energi och frekvens. Senare infördes namnet Plancks konstant h för denna proportionalitetskonstant.
År 1923 verifierade Arthur Compton sambandet återigen genom sitt experiment att sprida fotoner på elektroner, secomptonspridning .
Länk 1 är en intressant artikel om Max Planck och länk 2 beskriver den historiska utvecklingen av atomteorin.
/fa
Hej Ali! Bra fråga! Formeln för fotonens energi
E = hv (av konvention använder man oftast v [grekiska ny] för fotonens frekvens)
är ju så djupt rotad i den moderna fysiken att man kanske glömmer vad den kommer ifrån.
När det gäller fysikaliska samband uppkommer de typiskt på ett av två sätt:
1 ett experimentellt uppmätt samband eller lag
2 ett antagande som leder till andra samband som kan verifieras experimentellt
eller en kombination av 1 och 2
När det gäller fotonens energi är det till att börja med fall 2: Max Planck (
Bilden nedan från Wikimedia Commons
Plancks uttryck representerade uppmätta data mycket bra även för korta våglängder. Plancks antagande att energin var given av strålningens frekvens var en avvikelse från den klassiska teorin där energin gavs av amplituden hos strålningen. Utan att veta det förebådade Planck den kommande kvantmekaniken.
Einstein var i sin artikel om fotoelektriska effekten (1905) mycket tydlig med kvantiseringen, och införde begreppet foton för en "ljus-partikel". I fråga [2931] visas data för fotoelektriska effekten som visar proportionaliteten mellan energi och frekvens.
Det mest direkta beviset kom genom Bohrs atommodell (1913). Man kunde bygga upp energidiagram där skillnaden i energin mellan två tillstånd var lika med energin hos fotonen som utsändes vid en övergång. Man kunde mäta våglängden och med hjälp av det generella sambandet mellan vågens utbredningshastighet c, våglängden l och frekvensen v
c = lv
verifiera proportionaliteten mellan energi och frekvens. Senare infördes namnet Plancks konstant h för denna proportionalitetskonstant.
År 1923 verifierade Arthur Compton sambandet återigen genom sitt experiment att sprida fotoner på elektroner, se
Länk 1 är en intressant artikel om Max Planck och länk 2 beskriver den historiska utvecklingen av atomteorin.
/fa

Vad händer när man "curlar" i curling?
Fråga:
Hej! Skulle vilja veta vad som händer när man "curlar" i curling? Vad är det som gör att stenen glider bättre då?
/Hannes H, Alströmergymnasiet, Alingsås 2010-02-28
Hej! Skulle vilja veta vad som händer när man "curlar" i curling? Vad är det som gör att stenen glider bättre då?
/Hannes H, Alströmergymnasiet, Alingsås 2010-02-28
Svar:
Hannes! Intressant och aktuell fråga med tanke på lag Anette Norbergs insats i OS i Vancouver. Detaljerna för varför stenen "curlar" (avlänkas åt höger eller vänster i förhållande till den ursprungliga riktningen) är komplicerade och även kontroversiella. Vi behandlar detta i avsnittet mot slutet av svaret. Först en video om curling:
Vissa saker är man emellertid helt överens om:
1 Sopandet framför stenen skapar genom friktion värme som smälter isen och ger ett tunnt lager vatten. Detta minskar friktionen mellan stenen och isen.
2 Minskningen i friktion genom sopning medför dels att stenen går längre sträcka för en viss utgångshastighet och dels att den curlar (svänger) mindre.
3 Stenens curlande orsakas av friktionen mot isen och stenens rotation. Observera att man alltid sätter lite rotation på stenen: moturs om man vill att den curlar åt vänster och medurs om man vill ha en högerböj.
Till skillnad från andra sporter (t.ex. golf, bowling, skytte) kan man alltså påverka projektilens rörelse efter det att man släppt iväg den. Svårigheten är att man alltså får två effekter när man sopar: längre bana och mindre curl, och man måste besluta om en optimal kompromiss mellan effekterna.
SVTs kommentatorer vid OS-sändningarna från Vancouver spekulerade om vad resultatet skulle bli om det svenska damlaget skulle spela mot det svenska herrlaget. Man kom fram till att herrarna antagligen skulle vinna, men förklarade inte varför. Jag tror också herrarna skulle vinna helt enkelt för att de är tyngre och starkare, och kan på så sätt kontrollera stenen mer. Om man tittar på statistik för absoluta topp-curlare så har män c:a 90% och kvinnor c:a 80% lyckade stenar (slag).
Detaljerad förklaring till att stenen curlar
Låt oss börja med att göra ett enkelt experiment som du kan göra hemma. Ta ett köksglas (inte mormors finaste glas!) och leta upp ett jämnt, plant underlag, t.ex. en köksbänk. Vänd glaset upp-och-ner och skjut det längs bänken samtidigt som du sätter rotation på glaset, se vänstra bilden i nedanstående figur från Curling Science . Om du som i figuren roterar glaset medurs, så kommer glaset att avlänkas till vänster. Detta resultat är mycket förvånande för en curlare eftersom en curlingsten skulle avlänkas åt motsatt håll, se den högra bilden.
. Om du som i figuren roterar glaset medurs, så kommer glaset att avlänkas till vänster. Detta resultat är mycket förvånande för en curlare eftersom en curlingsten skulle avlänkas åt motsatt håll, se den högra bilden.
Varför reagerar glaset och curlingstenen olika på rotationen? Låt oss börja med att förklara varför glaset rör sig åt vänster. När glaset glider över bänken bromsas det up av en friktionskraft riktad rakt bakåt. Eftersom glasets tyngdpunkt ligger över bänkens plan, så kommer det att utsättas för ett vridmoment riktat bakåt. Trycket på framkanten av glaset blir då högre än trycket på bakkanten. Detta är samma effekt som att en bromsande bil får nosen nertryckt och en accelererande bil får nosen lyft. Eftersom glaset roterar får vi även en friktionskraft riktad åt vänster (friktionskraften är alltid motriktad rörelsen) i glasets framkant och en friktionskraft riktad åt höger i glasets bakkant. Eftersom normalkraften Fn enligt ovan är större i framkanten än i bakkanten blir friktionen större (se nedanstående formel), och vi kommer att få en nettokraft riktad åt vänster.
Varför uppför sig curlingsten annorlunda än glaset? För det första bör man veta att bottenytan på en curlingsten inte är plan, utan den har en skålformad fördjupning i mitten. Anläggningsytan mot isen är alltså en smal ring precis som för det upp-och-nervända glaset.
Skillnaden är att is smälter om den utsätts för högt tryck, se fasdiagrammet i fråga [12715]. Detta är skälet till att en kälke eller skridskor glider så bra på is - friktionen minskas genom ett tunnt vattenskikt. Precis som glaset utsätts stenen för en större normalkraft i framändan än i bakändan. I fallet curlingsten orsakar det högre trycket i framändan att friktionskoefficienten m minskar. Friktionskraften är ju
F = mFn (1)
Eftersom minskningen i friktionskoefficienten är större än ökningen i normalkraften kommer friktionskraften att bli mindre i framändan. Stenen kommer då att i stället böjas av åt höger.
Eftersom förklaringen bygger på att en del is smälts, så bör det ha betydelse vilken temperatur isen har. Om isens temperatur är mycket låg borde man vänta sig att den har svårare att smälta och att friktionen skulle bli större. I länk 1 sägs det om Scotts (Robert_Falcon_Scott ) sydpolsexpedition:
I What Puts the Curl in a Curling Stone? finns ovanstående förklaring till curlande och referenser till fyra vetenskapliga artiklar från Canadian Journal of Physics om olika aspekter på curling. The motion of curling rocks: Experimental investigation and semi-phenomenological description
finns ovanstående förklaring till curlande och referenser till fyra vetenskapliga artiklar från Canadian Journal of Physics om olika aspekter på curling. The motion of curling rocks: Experimental investigation and semi-phenomenological description är en senare artikel av samma författare. I den visas tydligt (men ganska svårgenomträngligt) att ovanstående modell är i stort sett korrekt även om vissa detaljer är oklara. Speciellt gäller detta hur stenen växelverkar med underlaget: växelverkar den med en fix isskiva eller med det rörliga vattnet under stenen? En annan effekt som är svår att förklara är att storleken av curl är i stort sett oberoende av stenens rotationshastighet. Intuitivt väntar man sig att en sten som roterar snabbare curlar mer.
är en senare artikel av samma författare. I den visas tydligt (men ganska svårgenomträngligt) att ovanstående modell är i stort sett korrekt även om vissa detaljer är oklara. Speciellt gäller detta hur stenen växelverkar med underlaget: växelverkar den med en fix isskiva eller med det rörliga vattnet under stenen? En annan effekt som är svår att förklara är att storleken av curl är i stort sett oberoende av stenens rotationshastighet. Intuitivt väntar man sig att en sten som roterar snabbare curlar mer.
I artikeln Comment on the motion of a curling rock framförs en annan modell där inte "våt friktion" (minskande friktionskoefficient) utan "torr friktion" (formel 1 ovan med konstant friktionskoefficient) används. Artikeln är emellertid inte av god kvalité, och slutsatserna är dubiösa.
framförs en annan modell där inte "våt friktion" (minskande friktionskoefficient) utan "torr friktion" (formel 1 ovan med konstant friktionskoefficient) används. Artikeln är emellertid inte av god kvalité, och slutsatserna är dubiösa.
Tester av modellerna
Det vore intressant att testa hur glaset uppför sig på is. Är det någon som har tillgång till mycket jämn is skulle jag vara tacksam om ni ville kummunicera era observationer till mig.
Ett annat experiment som är svårare att åstadkomma är att be ismakarna skruva upp kylningen till max. Skulle det gå att få ner temperaturen så mycket att man inte får någon smältning? Om det går skulle man få några mycket förvånade curlare: stenarna skulle bli mycket korta och curla åt fel håll :-)!
Sopforskning
Sopandet är uppenbarligen en mycket viktig del av curling eftersom detta är lagets möjlighet att påverka stenens bana sedan den släppts. Curling, Olympic training and ice friction fundamentals är ett anslag till några forskare för att förbättra chanserna för det brittiska damlandslaget att försvara sitt guld från 2002 i Turin 2006. Tydligen räckte inte pengarna, för som känt så vann ju lag Norberg!
är ett anslag till några forskare för att förbättra chanserna för det brittiska damlandslaget att försvara sitt guld från 2002 i Turin 2006. Tydligen räckte inte pengarna, för som känt så vann ju lag Norberg!
Vidare studier
Det finns som synes mycket i curling som är av fysikaliskt intresse, och då har vi inte tagit upp kollisioner mellan stenar och bevarandet av rörelsemängd och rörelseenergi.
För mer om curling se Wikipedia-artiklarna på engelska (Curling ) och på svenska (Curling ). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games
). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games . Länk 2 ger en alternativ förklaring.
. Länk 2 ger en alternativ förklaring.
Hannes! Intressant och aktuell fråga med tanke på lag Anette Norbergs insats i OS i Vancouver. Detaljerna för varför stenen "curlar" (avlänkas åt höger eller vänster i förhållande till den ursprungliga riktningen) är komplicerade och även kontroversiella. Vi behandlar detta i avsnittet mot slutet av svaret. Först en video om curling:
Vissa saker är man emellertid helt överens om:
1 Sopandet framför stenen skapar genom friktion värme som smälter isen och ger ett tunnt lager vatten. Detta minskar friktionen mellan stenen och isen.
2 Minskningen i friktion genom sopning medför dels att stenen går längre sträcka för en viss utgångshastighet och dels att den curlar (svänger) mindre.
3 Stenens curlande orsakas av friktionen mot isen och stenens rotation. Observera att man alltid sätter lite rotation på stenen: moturs om man vill att den curlar åt vänster och medurs om man vill ha en högerböj.
Till skillnad från andra sporter (t.ex. golf, bowling, skytte) kan man alltså påverka projektilens rörelse efter det att man släppt iväg den. Svårigheten är att man alltså får två effekter när man sopar: längre bana och mindre curl, och man måste besluta om en optimal kompromiss mellan effekterna.
SVTs kommentatorer vid OS-sändningarna från Vancouver spekulerade om vad resultatet skulle bli om det svenska damlaget skulle spela mot det svenska herrlaget. Man kom fram till att herrarna antagligen skulle vinna, men förklarade inte varför. Jag tror också herrarna skulle vinna helt enkelt för att de är tyngre och starkare, och kan på så sätt kontrollera stenen mer. Om man tittar på statistik för absoluta topp-curlare så har män c:a 90% och kvinnor c:a 80% lyckade stenar (slag).
Detaljerad förklaring till att stenen curlar
Låt oss börja med att göra ett enkelt experiment som du kan göra hemma. Ta ett köksglas (inte mormors finaste glas!) och leta upp ett jämnt, plant underlag, t.ex. en köksbänk. Vänd glaset upp-och-ner och skjut det längs bänken samtidigt som du sätter rotation på glaset, se vänstra bilden i nedanstående figur från Curling Science
Varför reagerar glaset och curlingstenen olika på rotationen? Låt oss börja med att förklara varför glaset rör sig åt vänster. När glaset glider över bänken bromsas det up av en friktionskraft riktad rakt bakåt. Eftersom glasets tyngdpunkt ligger över bänkens plan, så kommer det att utsättas för ett vridmoment riktat bakåt. Trycket på framkanten av glaset blir då högre än trycket på bakkanten. Detta är samma effekt som att en bromsande bil får nosen nertryckt och en accelererande bil får nosen lyft. Eftersom glaset roterar får vi även en friktionskraft riktad åt vänster (friktionskraften är alltid motriktad rörelsen) i glasets framkant och en friktionskraft riktad åt höger i glasets bakkant. Eftersom normalkraften Fn enligt ovan är större i framkanten än i bakkanten blir friktionen större (se nedanstående formel), och vi kommer att få en nettokraft riktad åt vänster.
Varför uppför sig curlingsten annorlunda än glaset? För det första bör man veta att bottenytan på en curlingsten inte är plan, utan den har en skålformad fördjupning i mitten. Anläggningsytan mot isen är alltså en smal ring precis som för det upp-och-nervända glaset.
Skillnaden är att is smälter om den utsätts för högt tryck, se fasdiagrammet i fråga [12715]. Detta är skälet till att en kälke eller skridskor glider så bra på is - friktionen minskas genom ett tunnt vattenskikt. Precis som glaset utsätts stenen för en större normalkraft i framändan än i bakändan. I fallet curlingsten orsakar det högre trycket i framändan att friktionskoefficienten m minskar. Friktionskraften är ju
F = mFn (1)
Eftersom minskningen i friktionskoefficienten är större än ökningen i normalkraften kommer friktionskraften att bli mindre i framändan. Stenen kommer då att i stället böjas av åt höger.
Eftersom förklaringen bygger på att en del is smälts, så bör det ha betydelse vilken temperatur isen har. Om isens temperatur är mycket låg borde man vänta sig att den har svårare att smälta och att friktionen skulle bli större. I länk 1 sägs det om Scotts (
Another key factor when considering the slipperiness of ice is temperature. Captain Scott noted during his Antarctic travels that once the temperature fell below -35 degrees C it become incredibly hard to pull sleds through the snow. This was because the heat produced by the friction between sled and snow was not enough to warm the ice to its melting point (0 degrees C) so no lubricating melt water was produced. Scott and his companions may as well have been pulling their sleds through sand. The closer the temperature of the ice is to its melting point the more melt lubricant is produced by sliding and the more slippery ice becomes.
I What Puts the Curl in a Curling Stone?
I artikeln Comment on the motion of a curling rock
Tester av modellerna
Det vore intressant att testa hur glaset uppför sig på is. Är det någon som har tillgång till mycket jämn is skulle jag vara tacksam om ni ville kummunicera era observationer till mig.
Ett annat experiment som är svårare att åstadkomma är att be ismakarna skruva upp kylningen till max. Skulle det gå att få ner temperaturen så mycket att man inte får någon smältning? Om det går skulle man få några mycket förvånade curlare: stenarna skulle bli mycket korta och curla åt fel håll :-)!
Sopforskning
Sopandet är uppenbarligen en mycket viktig del av curling eftersom detta är lagets möjlighet att påverka stenens bana sedan den släppts. Curling, Olympic training and ice friction fundamentals
Vidare studier
Det finns som synes mycket i curling som är av fysikaliskt intresse, och då har vi inte tagit upp kollisioner mellan stenar och bevarandet av rörelsemängd och rörelseenergi.
För mer om curling se Wikipedia-artiklarna på engelska (
 ). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games
). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games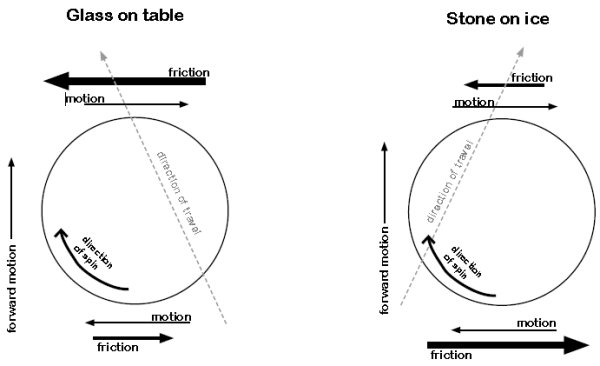
Vid backhoppning borde inte massan spela någon roll för hastigheten vid själva uthoppet (väl?).
Fråga:
Vid backhoppning borde inte massan spela någon roll för hastigheten vid själva uthoppet (väl?). Varför är det då en "trend" för backhoppare att de ska var så små som möjligt? Är det för att minska luftmotståndet?
/Sara L, Fredrikabremer gymnasiet, Haninge 2010-04-07
Vid backhoppning borde inte massan spela någon roll för hastigheten vid själva uthoppet (väl?). Varför är det då en "trend" för backhoppare att de ska var så små som möjligt? Är det för att minska luftmotståndet?
/Sara L, Fredrikabremer gymnasiet, Haninge 2010-04-07
Svar:
Sara! Intressant fråga, speciellt med tanke på tidigare svar om störtlopp! Jo, massan har betydelse för uthoppshastigheten. Se fråga [869] där det visas att hastigheten för en tyngre störtloppsåkare är större än för en mindre.
Hur kan det då komma sig att de bästa backhopparna ofta är små och lätta? En antydan får man om man jämför dräkterna. En störtloppsåkare har en tätsittande dräkt för att minimera luftmotståndet, medan en backhoppare har breda skidor och en dräkt som är "fem nummer för stor". Det är alltså inte farten i backen som bestämmer hopplängden utan förmågan att sväva långt i luften. För detta behöver man liten vikt och stor yta. Den stora ytan åstadkommer man dels med en väl tilltagen dräkt och dels med den s.k. V-stilen (Jan Boklöv,V-style ) som ger mer lyftkraft på kroppen eftersom den inte skuggas av skidorna - större "vinge" ger större lyftkraft. Hopplängden bestäms alltså till en stor del av aerodynamiken i luften.
En annan aspekt som gör farten i backen mindre utslagsgivande är att en stor del av uthoppshastigheten kommer från ett väl tajmat uthopp. Det är här och i förmågan att hålla kropp och skidor i en effektiv vinkel som skiljer bra hoppare från mindre bra.
Se vidare Backhoppning och
och Ski_jumping . Bilden nedan är från Wikimedia Commons.
/fa2010_4
Sara! Intressant fråga, speciellt med tanke på tidigare svar om störtlopp! Jo, massan har betydelse för uthoppshastigheten. Se fråga [869] där det visas att hastigheten för en tyngre störtloppsåkare är större än för en mindre.
Hur kan det då komma sig att de bästa backhopparna ofta är små och lätta? En antydan får man om man jämför dräkterna. En störtloppsåkare har en tätsittande dräkt för att minimera luftmotståndet, medan en backhoppare har breda skidor och en dräkt som är "fem nummer för stor". Det är alltså inte farten i backen som bestämmer hopplängden utan förmågan att sväva långt i luften. För detta behöver man liten vikt och stor yta. Den stora ytan åstadkommer man dels med en väl tilltagen dräkt och dels med den s.k. V-stilen (Jan Boklöv,
En annan aspekt som gör farten i backen mindre utslagsgivande är att en stor del av uthoppshastigheten kommer från ett väl tajmat uthopp. Det är här och i förmågan att hålla kropp och skidor i en effektiv vinkel som skiljer bra hoppare från mindre bra.
Se vidare Backhoppning
 och
och /fa2010_4

Vad är supersträngar?
Fråga:
Hej! Jag har tre frågor:
1. Vad är supersträngar?
2. Hur skulle universum se ut, och vad skulle vara annorlunda om vi hade <2 eller 4< rumsdimensioner?
3. Vad menas med att tyngdkraften är additiv? Innebär det att den är tio gånger så stor i en kropp med tio atomer än vad den är i en ensam atom, och 10^9 gånger starkare i en kropp med 10^9 atomer osv.?
/Axel O, Södermalmsskolan, Stockholm 2010-09-08
Hej! Jag har tre frågor:
1. Vad är supersträngar?
2. Hur skulle universum se ut, och vad skulle vara annorlunda om vi hade <2 eller 4< rumsdimensioner?
3. Vad menas med att tyngdkraften är additiv? Innebär det att den är tio gånger så stor i en kropp med tio atomer än vad den är i en ensam atom, och 10^9 gånger starkare i en kropp med 10^9 atomer osv.?
/Axel O, Södermalmsskolan, Stockholm 2010-09-08
Svar:
Axel! Detta är mycket svåra men aktuella frågor. Eftersom Stephen Hawking och Leonard Mlodinow just kommit ut med en bok, The Grand Design (länk 1), kan det vara på sin plats att sammanfatta var strängteorin står i dag. Nedanstående är till en del baserat på en artikel i Sunday Times vetenskapsbilaga Eureka från september 2010.
Strängteorin innebär att man beskriver elementarpartiklar som små endimensionella strängar. Dessa strängar vibrerar med olika frekvenser för att bilda olika partiklar. Det visade sig att det finns minst fem olika sträng-teorier med 10 rum/tid-dimensioner. Så småningom kom man fram till att alla var ekvivalenta med en teori med 11 dimensioner: M-teorin.
M-teorin
Enligt vissa teoretiker är M-teorin den ultimata TOE (Theory of Everything). Hawking ser M-teorin som ett underliggande karta som håller ihop olika teorier som beskriver alla naturlagar.
Det tycks som om ingen vet vad M-et i namnet kommer ifrån. Förutom Maybe (kanske) har jag sett Master (huvud-), Miracle (mirakulös) och Mystery (mysterium). Det tycks som om M-teorin är allt detta :-)!
I M-teorin har man alltså 11 rum/tid-dimensioner. Anledningen till att vi bara ser tre rumsdimensioner är att de övriga är kollapsade (eller kanske mer exakt, de har inte expanderat som de tre vi ser).
I M-teorin är man inte begränsad till endimensionella strängar, utan man kan ha vibrerande objekt (supersträngar) i 2 dimensioner (membran), 3 dimensioner (blobbar) och upp till 9 dimensioner.
Två fundamentala problem i dagens fysik är den spöklika obestämdheten hos kvantmekaniken (en atom kan befinna sig i flera tillstånd samtidigt) och det faktum att naturlagarna tycks vara finjusterade så att universum kunde utvecklas till ett universum som ger plats för liv - även om det bara finns på ett ställe, se diskussionen nedan.
M-teorin tillåter kanske 10500 olika universa med varierande naturlagar. Teorin tillåter, med hjälp av gravitationen, att universa skapas ur ingenting.
Universums utveckling och Guds existens
Mycket av diskussionen om Hawkings bok har handlat om behovet av en högre makt. Om man studerar universums utveckling från Big Bang till vad vi observerar i dag, visar det sig att många av naturlagarna verkar avstämda för att producera en värld där liv är möjligt. Några exempel (bland många) på denna finjustering av naturlagarna är
Ovanstående egenskaper kan förklaras på ett av tre sätt
Hawking förespråkar punkt 3: Gud i punkt 1 behövs inte.
Några kommentarer
Eftersom M-teorin ännu inte kan knytas till observationer kan man ha olika åsikter om teorin:
Den är "Kejsarens nya kläder" eller pseudovetenskap av noll och intet värde. Eller Hawkings optimistiska åsikt att det kan vara den ultimata teorin som förklarar allting: "Philosophy is dead and there is no need for the God hypothesis: modern cosmology has all the answers".
Jag tror att de flesta av dagens fysiker anser att det är en lovande början och låter teoretikerna hållas ett tag till så de får en chans att komma upp med några förutsägelser som kan testas med experiment. Bilden nedan från ett föredrag av Lawrence M Krauss (se fråga [18978]) är en mindre positiv synpunkt.
Jag har en kanske naiv uppfattning att en modell eller teori skall vara behjälplig för att "förstå" ett fysikaliskt fenomen. För mig uppfyller M-teorin inte detta kriterium med sina 10500 universa. Men för all del, redan kvantmekaniken är obegriplig.
Vad gäller din sista fråga, så har jag inte sett uttrycket, men jag tror din tolkning är korrekt: helt enkelt att kraften är proportionell mot massan, F=mg.
Axel! Detta är mycket svåra men aktuella frågor. Eftersom Stephen Hawking och Leonard Mlodinow just kommit ut med en bok, The Grand Design (länk 1), kan det vara på sin plats att sammanfatta var strängteorin står i dag. Nedanstående är till en del baserat på en artikel i Sunday Times vetenskapsbilaga Eureka från september 2010.
M-teorin
Enligt vissa teoretiker är M-teorin den ultimata TOE (Theory of Everything). Hawking ser M-teorin som ett underliggande karta som håller ihop olika teorier som beskriver alla naturlagar.
Det tycks som om ingen vet vad M-et i namnet kommer ifrån. Förutom Maybe (kanske) har jag sett Master (huvud-), Miracle (mirakulös) och Mystery (mysterium). Det tycks som om M-teorin är allt detta :-)!
I M-teorin har man alltså 11 rum/tid-dimensioner. Anledningen till att vi bara ser tre rumsdimensioner är att de övriga är kollapsade (eller kanske mer exakt, de har inte expanderat som de tre vi ser).
I M-teorin är man inte begränsad till endimensionella strängar, utan man kan ha vibrerande objekt (supersträngar) i 2 dimensioner (membran), 3 dimensioner (blobbar) och upp till 9 dimensioner.
Två fundamentala problem i dagens fysik är den spöklika obestämdheten hos kvantmekaniken (en atom kan befinna sig i flera tillstånd samtidigt) och det faktum att naturlagarna tycks vara finjusterade så att universum kunde utvecklas till ett universum som ger plats för liv - även om det bara finns på ett ställe, se diskussionen nedan.
M-teorin tillåter kanske 10500 olika universa med varierande naturlagar. Teorin tillåter, med hjälp av gravitationen, att universa skapas ur ingenting.
Universums utveckling och Guds existens
Mycket av diskussionen om Hawkings bok har handlat om behovet av en högre makt. Om man studerar universums utveckling från Big Bang till vad vi observerar i dag, visar det sig att många av naturlagarna verkar avstämda för att producera en värld där liv är möjligt. Några exempel (bland många) på denna finjustering av naturlagarna är
- Om den starka kärnkraften bara varit lite starkare så hade 2He varit stabilt och stjärnor hade inte kunnat bildas.
- Om det inte funnits ett tillstånd i 12C som precis passar till energin hos 3 a-partiklar, så hade ämnen tyngre än kol (som behövs för liv) inte kunnat bildas.
- Endast ett universum med 3 utvecklade rumsdimensioner tillåter stabila planetbanor och följaktligen liv, åtminstone som vi känner det.
Ovanstående egenskaper kan förklaras på ett av tre sätt
- Det finns en högre makt som bestämt att det skall vara så (den klassiska religiösa skapelseteorin).
- Det är en ytterst osannolik slump.
- Det finns massor av universa med olika egenskaper. Ett av dessa är vårt med de nödvändiga egenskaperna. De övriga "misslyckade" universa finns, men de innehåller inget intelligent liv som kan fundera på varför deras värld ser ut som den gör.
Hawking förespråkar punkt 3: Gud i punkt 1 behövs inte.
Några kommentarer
Eftersom M-teorin ännu inte kan knytas till observationer kan man ha olika åsikter om teorin:
Den är "Kejsarens nya kläder" eller pseudovetenskap av noll och intet värde. Eller Hawkings optimistiska åsikt att det kan vara den ultimata teorin som förklarar allting: "Philosophy is dead and there is no need for the God hypothesis: modern cosmology has all the answers".
Jag tror att de flesta av dagens fysiker anser att det är en lovande början och låter teoretikerna hållas ett tag till så de får en chans att komma upp med några förutsägelser som kan testas med experiment. Bilden nedan från ett föredrag av Lawrence M Krauss (se fråga [18978]) är en mindre positiv synpunkt.
Jag har en kanske naiv uppfattning att en modell eller teori skall vara behjälplig för att "förstå" ett fysikaliskt fenomen. För mig uppfyller M-teorin inte detta kriterium med sina 10500 universa. Men för all del, redan kvantmekaniken är obegriplig.
Vad gäller din sista fråga, så har jag inte sett uttrycket, men jag tror din tolkning är korrekt: helt enkelt att kraften är proportionell mot massan, F=mg.

Arbete på ett löpband
Fråga:
Min fru springer på ett löpband som går att luta. Jag påstår att hon i teknisk mening inte utför mer arbete när det lutar uppåt eftersom henne massa inte flyttas uppåt. Hon påstår att det går tyngre (jag har inte provat). Denna känsla av att det går tyngre har enl. mig möjligen en fysiologisk förklaring som jag inte kan beskriva.
/Bertil S, Hackås 2010-11-20
Min fru springer på ett löpband som går att luta. Jag påstår att hon i teknisk mening inte utför mer arbete när det lutar uppåt eftersom henne massa inte flyttas uppåt. Hon påstår att det går tyngre (jag har inte provat). Denna känsla av att det går tyngre har enl. mig möjligen en fysiologisk förklaring som jag inte kan beskriva.
/Bertil S, Hackås 2010-11-20
Svar:
Tyvärr Bertil, din fru har rätt (igen :-))! Man kan resonera på flera sätt, till exempel: När foten är i kontakt med bandet transporteras den lite neråt. Detta måste kompenseras i nästa steg, så det är en riktig uppförsbacke. Om du tittar noga så flyttar sig tyngdpunkten på löparen upp och ner. Om bandet lutar, så måste denna rörelse vara större för att löparen skall komma rätt i nästa steg. Att springa på ett löpband är helt ekvivalent med normal löpning med undantag för luftmotståndet.
Andra, eventuellt förvånande, fakta är att man kan bli trött utan att utföra arbete (fråga [13327]) och att utfört arbete beror på vilket inertialsystem man befinner sig i (fråga [14380]).
/Peter E 2010-11-20
Tyvärr Bertil, din fru har rätt (igen :-))! Man kan resonera på flera sätt, till exempel: När foten är i kontakt med bandet transporteras den lite neråt. Detta måste kompenseras i nästa steg, så det är en riktig uppförsbacke. Om du tittar noga så flyttar sig tyngdpunkten på löparen upp och ner. Om bandet lutar, så måste denna rörelse vara större för att löparen skall komma rätt i nästa steg. Att springa på ett löpband är helt ekvivalent med normal löpning med undantag för luftmotståndet.
Andra, eventuellt förvånande, fakta är att man kan bli trött utan att utföra arbete (fråga [13327]) och att utfört arbete beror på vilket inertialsystem man befinner sig i (fråga [14380]).
/Peter E 2010-11-20
Har ljusets olika färger olika hastighet?
Fråga:
Har ljusets olika färger olika hastighet?
Enligt fråga [17367] så får jag en liten förklaring till varför ljusets bryts när det träffar ett tätare medium.
Det som jag inte blir klok på är att det i fysikböckerna (delvis förenklat) står att detta beror på att ljusets hastighet ändras, att det sänks när det träffar det tätare mediet. Ju långsammare ljuset går desto större blir brytningen.
Eftersom ljuset färger bryts olika så säger den principen då att de olika färgerna har olika hastigheter genom ett tätare medium. Bör detta då inte betyda att det gäller för alla olika medium? Tar vi det ett steg längre borde det violetta ljuset, som bryts mest, ha den lägsta hastigheten och därför nå jorden allra sist, om vi tittar på en specifik partikel eller vågrörelse som lämnar solen.
Hur ska vi förhålla oss till detta med våra elever som gärna ställer invecklade frågor men som har svårt att förstå en del fakta.
/Petri M, Mariefreds skola, Mariefred 2011-02-16
Har ljusets olika färger olika hastighet?
Enligt fråga [17367] så får jag en liten förklaring till varför ljusets bryts när det träffar ett tätare medium.
Det som jag inte blir klok på är att det i fysikböckerna (delvis förenklat) står att detta beror på att ljusets hastighet ändras, att det sänks när det träffar det tätare mediet. Ju långsammare ljuset går desto större blir brytningen.
Eftersom ljuset färger bryts olika så säger den principen då att de olika färgerna har olika hastigheter genom ett tätare medium. Bör detta då inte betyda att det gäller för alla olika medium? Tar vi det ett steg längre borde det violetta ljuset, som bryts mest, ha den lägsta hastigheten och därför nå jorden allra sist, om vi tittar på en specifik partikel eller vågrörelse som lämnar solen.
Hur ska vi förhålla oss till detta med våra elever som gärna ställer invecklade frågor men som har svårt att förstå en del fakta.
/Petri M, Mariefreds skola, Mariefred 2011-02-16
Svar:
Brytningsindex (Refractive_index , brytningsindex ) n eller optisk täthet hos ett medium definieras som ljushastigheten i vakuum dividerat med ljusets hastighet i mediet v: n = c/v.
I ett medium med brytningsindex n>1 har olika våglängder olika hastighet. Hastigheten är c/n där c är ljushastigheten i vakuum. Observera emellertid att hastigheten i vakuum är c för alla våglängder eftersom n=1.
Ja det är korrekt att ju långsammare ljuset går (ju större n) desto mer brytning får man, se fråga [17367] och [3302].
Eftersom ljushastigheten i vakuum alltid är densamma så uppkommer inte problemet att vi ser olika tider i olika våglängder. Om rymden mellan jorden och solen varit av glas, så hade vi sett rött ljus snabbare är blått.
Den klassiska förklaringen förljusbrytning (refraktion , Refraktion ) är en rad soldater som marscherar snett in mot en rak gränslinje till en leråker. Soldaternas marschhastighet minskar när de kommer till leråkern. För att bevara den snygga räta linjen med
) är en rad soldater som marscherar snett in mot en rak gränslinje till en leråker. Soldaternas marschhastighet minskar när de kommer till leråkern. För att bevara den snygga räta linjen med
soldater bredvid varandra, så måste de ändra riktning lite mot normalens riktning. Om vi sedan har en rad med kortbenta soldater som har ännu mindre hastighet
i leråkern, så behöver dessa avvika ännu mer från utgångsvinkeln. (Vi vill bara inte tänka på vad som skulle hända om vi blandade långbenta och kortbenta soldater i en rad :-).)
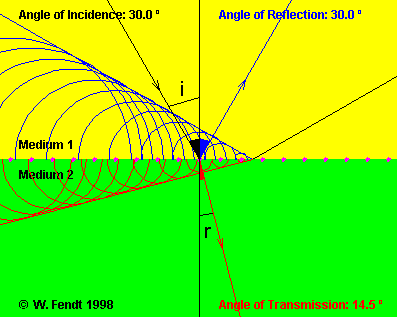
OK med soldater som kan bestämma att de behöver avvika från rakt fram, men hur vet ljuset hur det skall avvika? Helt enkelt genom att vågor i oordning tenderar att släcka ut varandra (interferens). I alla riktningar utom den som specificeras av brytningslagen släcks alltså ljuset ut. Se bilden nedan.
Din sista fråga finns behandlad ifysik, förståelse av .
Huvudpunkterna är:
Man kan heller inte begära att en lärare skall kunna besvara allt. Även jag, med 40 års erfarenhet av fysik, går bet på en del frågor (ofta de som verkar triviala till att börja med). Jag kan emellertid oftast förstå när jag slår upp ett fenomen, men att göra det lättbegripligt för var och en kan vara svårt eller omöjligt. Det är en del i läroprocessen att man med tiden och erfarenheten förhoppningsvis får en allt djupare förståelse för fysik - allt kan inte komma på en gång! Det är lätt
att lära sig att Gustav II Adolf dog en novemberdag 1632 på ett fält nära Lützen, men kanske lite längre att förstå vad han hade där att göra!
Se en avancerad framställning av problemet i länk 1.
En kommentar om förståelse av fysik (Jocelyn_Bell ):
(Jocelyn Bell är en av upptäckarna av pulsarer.)
I ett medium med brytningsindex n>1 har olika våglängder olika hastighet. Hastigheten är c/n där c är ljushastigheten i vakuum. Observera emellertid att hastigheten i vakuum är c för alla våglängder eftersom n=1.
Ja det är korrekt att ju långsammare ljuset går (ju större n) desto mer brytning får man, se fråga [17367] och [3302].
Eftersom ljushastigheten i vakuum alltid är densamma så uppkommer inte problemet att vi ser olika tider i olika våglängder. Om rymden mellan jorden och solen varit av glas, så hade vi sett rött ljus snabbare är blått.
Den klassiska förklaringen för
 ) är en rad soldater som marscherar snett in mot en rak gränslinje till en leråker. Soldaternas marschhastighet minskar när de kommer till leråkern. För att bevara den snygga räta linjen med
) är en rad soldater som marscherar snett in mot en rak gränslinje till en leråker. Soldaternas marschhastighet minskar när de kommer till leråkern. För att bevara den snygga räta linjen medsoldater bredvid varandra, så måste de ändra riktning lite mot normalens riktning. Om vi sedan har en rad med kortbenta soldater som har ännu mindre hastighet
i leråkern, så behöver dessa avvika ännu mer från utgångsvinkeln. (Vi vill bara inte tänka på vad som skulle hända om vi blandade långbenta och kortbenta soldater i en rad :-).)
OK med soldater som kan bestämma att de behöver avvika från rakt fram, men hur vet ljuset hur det skall avvika? Helt enkelt genom att vågor i oordning tenderar att släcka ut varandra (interferens). I alla riktningar utom den som specificeras av brytningslagen släcks alltså ljuset ut. Se bilden nedan.
Din sista fråga finns behandlad i
Huvudpunkterna är:
- Utgå från observationer - fysik är inte matematik utan en empirisk (erfarenhetsbaserad, Empiri
 ) vetenskap
) vetenskap
- "Varför?" kan vi aldrig besvara eftersom det implicerar avsikt (och i så fall, vems avsikt). Man kan emellertid besvara "hur?" och ge samband mellan olika fysikaliska fenomen
- En del av den teoretiska fysiken är helt enkelt svår att förstå, så vi får lita på vad våra vänner teoretikerna säger åtminstone vad gäller väl etablerade fenomen
Man kan heller inte begära att en lärare skall kunna besvara allt. Även jag, med 40 års erfarenhet av fysik, går bet på en del frågor (ofta de som verkar triviala till att börja med). Jag kan emellertid oftast förstå när jag slår upp ett fenomen, men att göra det lättbegripligt för var och en kan vara svårt eller omöjligt. Det är en del i läroprocessen att man med tiden och erfarenheten förhoppningsvis får en allt djupare förståelse för fysik - allt kan inte komma på en gång! Det är lätt
att lära sig att Gustav II Adolf dog en novemberdag 1632 på ett fält nära Lützen, men kanske lite längre att förstå vad han hade där att göra!
Se en avancerad framställning av problemet i länk 1.
En kommentar om förståelse av fysik (
(Jocelyn Bell är en av upptäckarna av pulsarer.)
Jocelyn Bell was born in Belfast, Northern Ireland, where her father was an architect who helped design the Armagh Planetarium. She was encouraged to read and drawn to books on astronomy. She lived in Lurgan as a child and attended Lurgan College where she was one of the first girls there who was permitted to study science. Previously, the girls' curriculum had included such subjects as cross-stitching and cooking.
At age eleven, she failed the 11+ exam and her parents sent her to the Mount School, York, a Quaker girls' boarding school. There she was impressed by a physics teacher, Mr. Tillott, who taught her:
You don't have to learn lots and lots ... of facts; you just learn a few key things, and ... then you can apply and build and develop from those ... He was a really good teacher and showed me, actually, how easy physics was.
Varför har nyhuggen ved sämre eldningsvärde än torr ved?
Fråga:
Varför har nyhuggen ved sämre eldningsvärde än torr ved?
/Per O, Borgarskolan, Malmö 2011-10-27
Varför har nyhuggen ved sämre eldningsvärde än torr ved?
/Per O, Borgarskolan, Malmö 2011-10-27
Svar:
Nyhuggen ved innehåller mycket mer vatten än torkad ved. Det traditionella svaret är att vattnets ångbildningsvärme är stor, och att alltså mycket energi förloras till att förånga vatten. Låt oss göra en kvantitativ uppskattning.
Energiinnehållet i torr ved är enligtEnergy_densityCommon_energy_densities 16 MJ/kg. Ångbildningsvärmet för vatten är 2.3 MJ/kg. Om vatteninnehållet är 30% så utvecklas 0.716=11.2 MJ. För att förånga vatteninnehållet går det åt 0.32.3=0.7 MJ. Nettoenergiinnehållet blir alltså 11.2-0.7=10.5 MJ. Förhållandet torr ved/fuktig ved blir alltså 16/10.5=1.5.
Det mesta av effektförlusten kommer sig av att vattnet inte ger något bidrag till energiutvecklingen. Totalt sett är det alltså inte ångbildningsvärmet som är den stora effekten utan det faktum att massa försvinner vid torkning. Den fuktiga vedklabben ger alltså nästan samma totala energiutveckling om man torkar den.
Men den som eldat med fuktig och torr ved vet att det är en enorm skillnad! Det måste alltså vara en annan effekt som dominerar, t.ex. hur effektivt värmen transporteras till rummet.
Det är självklart att torr ved brinner bättre (vid högre temperatur) än fuktig ved. Den utstrålade effekten per m2 ges av Stefan-Boltzmanns lag (Stefan–Boltzmann_law ):
P = sT4
där konstanten s=5.6710-8 W/m2/K4 och T är den absoluta temperaturen i kelvin. Vi har alltså för strålning ett mycket häftigt beroende av temperaturen. Låt oss anta att temperaturen är 1000 K med torr ved och 750 K med fuktig. Strålningen är då 1.334=3 gånger högre för torr ved. (De uppskattade temperaturerna är från länk 1 sidan 4.)
Men vi måste självklart bevara den totala energin, hur går det ihop? Om förbränningen sker långsamt vid lägre temperatur kommer en större andel av värmen försvinna ut i skorstenen. Eftersom man knappast vill ha någon konvektion (strömning) av rökgaser ut i rummet, så är det strålningen (värmestrålning och synligt ljus) som värmer upp spisen och rummet. Effektiviteten hos spisen är alltså mycket beroende på temperaturen, som i sin tur beror av fuktinnehållet i veden.
Se ävenWood_fuel . Nedanstående bild är därifrån.
Nyhuggen ved innehåller mycket mer vatten än torkad ved. Det traditionella svaret är att vattnets ångbildningsvärme är stor, och att alltså mycket energi förloras till att förånga vatten. Låt oss göra en kvantitativ uppskattning.
Energiinnehållet i torr ved är enligt
Det mesta av effektförlusten kommer sig av att vattnet inte ger något bidrag till energiutvecklingen. Totalt sett är det alltså inte ångbildningsvärmet som är den stora effekten utan det faktum att massa försvinner vid torkning. Den fuktiga vedklabben ger alltså nästan samma totala energiutveckling om man torkar den.
Men den som eldat med fuktig och torr ved vet att det är en enorm skillnad! Det måste alltså vara en annan effekt som dominerar, t.ex. hur effektivt värmen transporteras till rummet.
Det är självklart att torr ved brinner bättre (vid högre temperatur) än fuktig ved. Den utstrålade effekten per m2 ges av Stefan-Boltzmanns lag (
P = sT4
där konstanten s=5.6710-8 W/m2/K4 och T är den absoluta temperaturen i kelvin. Vi har alltså för strålning ett mycket häftigt beroende av temperaturen. Låt oss anta att temperaturen är 1000 K med torr ved och 750 K med fuktig. Strålningen är då 1.334=3 gånger högre för torr ved. (De uppskattade temperaturerna är från länk 1 sidan 4.)
Men vi måste självklart bevara den totala energin, hur går det ihop? Om förbränningen sker långsamt vid lägre temperatur kommer en större andel av värmen försvinna ut i skorstenen. Eftersom man knappast vill ha någon konvektion (strömning) av rökgaser ut i rummet, så är det strålningen (värmestrålning och synligt ljus) som värmer upp spisen och rummet. Effektiviteten hos spisen är alltså mycket beroende på temperaturen, som i sin tur beror av fuktinnehållet i veden.
Se även

Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.
Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar

