Svar:
Det är ingen lätt fråga att ge ett kort och uttömmande svar på. Effekten kallas för magnuseffekten. I många böcker finns det missvisande "förklaringar" till fenomenet. Se länk 1 för en avancerad beskrivning av magnuseffekten och aerodynamisk lyftkraft för en flygplansvinge. I Magnus_effect finns en parametrisering av storleken på lyftkraften.

Låt oss i den följande diskussionen anta att vi har slagit en
underskruvad boll. Tänk på bordtennis eller golf! Bollen får då en uppåtriktad
kraft på grund av rotationen.

En viktig princip i strömningslära är att luften häftar vid bollen. Vid bollens yta
finns alltså ett tunt luftlager som följer med bollen.

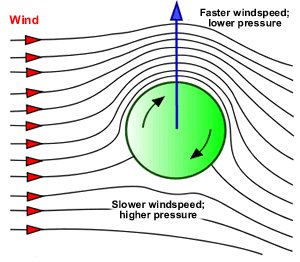
Det är rätt lätt att övertyga sig om att luften strömmar fortare ovanför än under bollen.
(Vi betraktar luftens hastighet relativt bollen.) Luften som går snabbare över bollen måste accelereras. För detta krävs en tryckskillnad. Trycket
är alltså lägre rakt över bollen än långt bort från bollen. Med samma argument visar
man att trycket är högre strax under bollen. Tryckkrafterna påverkar alltså bollen uppåt! Se nedanstående figur.

Ett annat sätt att se problemet är att bollens rotation "drar isär" luften på ovansidan och "trycker ihop" luften på undersidan. Vi får alltså lågt tryck på ovansidan och högt tryck på undersidan. Denna tryckskillnad ger upphov till en lyftkraft.

Experiment: Be en kamrat slå en bordtennisboll hårt med mycket underskruv. Stå vid sidan och studera bollbanan. En golfboll beter sig likadant men är svårare att studera.

/ Gunnar O/lpe 1999-06-27

Svar:

Detta påstås ofta av kommentatorer, men ligger det något i det? Det mest väsentliga är luftmotståndet (friktion). Det är i princip luftmotståndet som bestämmer hastigheten. Vad händer då med en skidåkare som lägger på hullet? Jo han eller hon blir lite större och lite tyngre. Men eftersom volymen av en ideal klotformig skidåkare går som r³ medan ytan går som r², så ökar massan snabbare än ytan med faktorn r. Kraften som drar skidåkaren nedåt är ju proportionell mot massan, medan kraften som bromsar är proportionell mot ytan. Vi får allstå en större kraft för den tyngre skidåkaren, medan luftmotståndet inte ökar lika mycket. Så om allt annat är lika så har en tyngre åkare en fördel. Vad gäller glidfriktion mellan snön och skidorna är den propotionell mot normalkraften som är proportionell mot massan. För denna har alltså skidåkarens vikt ingen betydelse eftersom både friktionen och den dragande kraften är proportionell mot massan. Se även fråga [20012].

/PE 2026-02-03

Svar:
Enligt den förenklade teorin för friktion som presenteras i skolfysiken så beror inte friktionskraftens storlek på kontaktytans area utan endast på normalkraftens storlek. I praktiken är det däremot så att friktionskraften ökar med arean. Breda däck ger större friktionskraft och bättre väghållning. Med dubbar blir effekten ännu större eftersom ett bredare däck hat plats för fler dubbar.

Dessutom förkortas bromssträckan och accelerationen blir bättre. Friktionstalet för kontakt gummi - asfalt är ca 1,5 för bra gummiblandningar och varma däck.

Friktionen mot asfalt är, kanske lite förvånande, större om man har omönstrade däck än om man har mönstrade. Anledningen till att däck på vanliga bilar är mönstrade är framför allt för att eventuellt vatten skall komma undan. Tänk på formel-1 bilar: vid torrt väder använder man omönstrade däck, men om det börjar regna måste man omedelbart byta annars kommer bilarna att vattenplana av banan.

Fundera: Varför har man vingar på formel 1-bilar?

Fundera: Hur fort kan man köra genom en kurva med en radie på 100 m? Antag att normalkraften är lika stor som tyngdkraften.
/GO 2003-02-02

Svar:
Om vinden kommer rakt bakifrån går det inte. Om vinden kommer från sidan, har båtens hastighet inte så mycket med vindens hastighet att göra.

Vindens verkan på seglet resulterar i en kraft, som verkar på båten genom masten. Vilken hastighet båten får beror på båtskrovet. En klumpig båt går långsamt. En långsmal, smäcker båt går snabbt, och den hastigheten kan vara större än vindens.

Det finns en detaljerad förklaring under länk 1. Om vinden kommer snett framifrån tvingas den av seglet att vrida lite i riktning mot segelbåtens akter. Detta leder enligt regeln verkan och återverkan (Newtons tredje lag, se Newtons rörelselagar), till en kraft med en komponent riktad mot fören. Det finns naturligtvis även en kraftkomponent i sidled, men segelbåtens köl hindrar båten att driva i sidled.
/KS 2001-04-04

Svar:
En kastparabel är den bana som ett föremål som kastas beskriver då föremålet endast påverkas av tyngdaccelerationen i ett gravitationsfält och där hastigheten i horisontalled är större än noll.

För fallet utan luftmotstånd är det lätt att bevisa att den optimala utkastvinkeln är 45^o. Vi kallar utgångsvinkeln x^o. Vi delar upp rörelsen i två komponenter: en horisontell med konstant hastighet och en vertikal med accelerationen g nedåt. Om utgångshastigheten är v blir den vertikala komponenten v sin(x) och den horisontella v cos(x).

Från den vertikala rörelsen kan vi räkna ut hur lång tid det tar för det kastade föremålet att falla från en viss höjd så att dess sluthastighet är v sin(x):

v sin(x) = gt

Eftersom fallet är spegelbilden av uppfärden (detta gäller bara om vi kan bortse från luftmotståndet) blir den totala tiden för hela kaströrelsen 2t:

2t = 2v sin(x)/g (1)

Det horisontella rörelsen sker med konstant hastighet, så kastlängden s ges av:

s = v cos(x) (2t) = v cos(x) (2v sin(x)/g)

dvs

s = 2v² sin(x) cos(x)/g = v² sin(2x)/g (2)

Maximum för sin(2x) uppnås för 2x = 90^o, dvs
den optimala utkastvinkeln är 45^o.

Vi kan från ekvation 1 även räkna ut maxhöjden h:

t = v sin(x)/g

h = gt²/2 = g((v sin(x))/g)²/2

dvs

h = (v sin(x))²/2g (3)

Vi kan räkna ut h även från att kinetiska energin i x-led vid utkastögonblicket skall vara lika med den potentiella energin i vändläget (höjden h):

m(v sin(x))²/2 = mgh

dvs

h = (v sin(x))²/2g

vilket är samma uttryck som (3).

Länk 1 ger ett uttryck för den optimala vinkeln om man tar hänsyn till att utkastpunkten ligger högre än landningspunkten. Den optimala vinkeln blir då lite mindre än 45^o.

Sedan är det en annan sak att utgångsvinkeln i verkligheten för de flesta relevanta grenar (t.ex. kulstötning) är betydligt mindre än 45^o. Utgångsvinkeln varierar också mellan olika idrottare. Detta beror på fysiologi och att ansatsen sker i horisontalplanet. Det går alltså att få en högre utgångshastighet om man minskar utgångsvinkeln något. Optimeringsproblemet blir då lite mer komplicerat. Om man tar hänsyn till luftmotståndet visar det sig att den optimala vinkeln blir mindre är 45^o.
/Peter E 2004-12-09

Svar:
Problemet är på grund av luftens inverkan mycket mer komplicerat. En golfboll rör sig inte alls i en kastparabel eftersom luften spelar mycket stor roll. För ett mellanjärn är banan sedd från sidan närmast hypotenusan av en rätvinklig triangel.

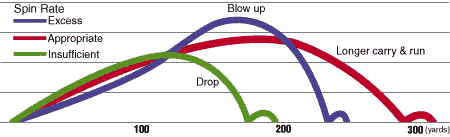
Spinnet och dimplarna (de små groparna) på en golfboll minskar för det första luftmotståndet (genom turbulens) och ger dessutom upphov till en lyftkraft (genom den sk Magnus-effekten). Bilden (från nedanstående länk Flight Dynamics of Golf Balls) visar bollbanan för olika spinn. Det är uppenbart viktigt all få lagom spinn på bollen!

Se Golf Ball Flight Dynamics och nedanstående länkar för olika aspekter på golfbollars rörelse.

Se även kastparabel för rörelse utan hänsyn till luftens inverkan.

/Peter E 2005-06-25

Svar:
Ditt problem är inte helt lätt, du får nöja dig med en skiss. Lösningen finns under länk 1, men där på engelska.

Vi börjar med att bortse från kulans rotation. Antag kulans massa är m och dess sluthastighet v. Då gäller enligt energiprincipen (potentiell energi på höjden h = kinetisk energi vid botten):

mgh = mv²/2

dvs

v² = 2gh

Om kulan inte glider alls kommer den att sättas i rotation. Om tyngdpunktens hastighet i detta fallet är u, kommer vinkelhastigheten w att vara u/r där r är kulans radie. (Du får detta resultat eftersom den del av kulan som rör vid kulbanan har hastigheten 0 i förhållande till banan - kom ihåg, inget glid!).

En homogen kulas tröghetsmoment ges av J = 2mr²/5 (TröghetsmomentExempel) och rotationsenergin är Jw²/2.

Vi adderar translations-kinetiska energin och rotationsenergin och får

mgh = mu²/2 + (2mr²/5)(u/r)²/2 = mu²(1/2) + mu²(1/5)

dvs

u² = (10/7)gh = 1.43gh

Detta är klart mindre än 2gh som vi fick ovan eftersom ju en del energi går till kulans rotationsenergi. Förhållandet u/v blir ungefär 0.85, alltså 15% lägre hastighet än en kula som glider perfekt och inte roterar.

Förhållandet mellan rotationsenergi och translationsenergi blir enligt ovan

(1/5)/(1/2) = 2:5.

Tillägg om puttning i golf

Golfspelare som puttar bra ser till att slå till bollen med en något uppåtgående rörelse för att bollen om möjligt skall börja rulla omedelbart. Om man slår till bollen helt centralt kommer bollen att glida ett tag på gräset. Friktionen kommer efter ett tag att få bollen att rulla, men rotationsenergin måste tas från rörelseenergin. Bollen bromsas alltså upp för att den skall kunna få rotation. Det visar sig att längden på puttarna blir mycket mer konsistent om man kan få bollen att rulla direkt vid tillslaget.

Tekniken att få överspinn på bollen direkt vid tillslaget används även t.ex. i biljard då man oftast slår till bollen ovanför ekvatorsplanet vilket får bollen att börja rulla omedelbart.

/fa
/Peter E 2006-05-16

Svar:
Hej Johan!

Nej, jag kan inte förklara problemet. Men jag tror inte heller att olika material skruvar åt olika håll. Tänk t.ex. på en golfboll och en pingisboll. Båda påverkas på samma sätt av underskruv - de påverkas av en kraft uppåt. Detta trots att de har helt olika ytor: golfbollen är knottrig vilket ger turbulent strömning och pingisbollen är slät vilket ger laminär strömning kring bollen. Dessutom finns det ju fotbollar både av plast och av läder, och jag tror en spelare skulle bli mycket förvånad om en ny boll skruvade åt fel håll :-).

Skruv och lyft hos roterande bollar förklaras av den s.k. Magnuseffekten som bygger på Bernoullis ekvation - högre hastighet hos luften ger lägre tryck (Bernoulli's_principle). Se även Magnus_effect.

En helt annan effekt är skruvade kast i kricket, men där har man en asymmetri hos bollen och skruven är riktad i samma riktning som asymmetrin - en underskruvad kricketboll avviker i sidled i stället för i höjdled. Se Swing_bowling.

Se skruvad boll, golfboll och en artikel om fotbollsfysik under länk 1.

Tillägg januari 2017

Magnuseffekten är ett fysikaliskt fenomen som uppträder för roterande kroppar. Effekten innebär att en kropp som rör sig genom en fluid (en vätska eller en gas) samtidigt som den roterar accelereras vinkelrätt mot rörelseriktningen, det vill säga att rörelseriktningen "böjs av". Det är den fysikaliska kraft som gör att roterande bollar får så kallad skruv inom olika bollsporter, se Magnuseffekten och fråga [754].

Video som visar och förklarar Magnuseffekten:



Jag kan inte, trots omfattande sökningar, hitta något väldokumenterat exempel på att materialet i bollen skulle ha någon betydelse. Strukturen på ytan påverkar storleken på Magnus-kraften (dimplarna på en golfboll ökar t.ex. effekten betydligt), men att ett alternativt material skulle ändra kraftens riktning låter inte sannolikt.

Enligt beskrivningen ovan är det plastbollen som uppför sig som väntat. En höger utsida roterar bollen medurs, vilket ger en avvikelse åt höger (den av golfaren fruktade slicen). Kan det vara så att en läderboll är lite asymmetrisk pga en söm (se cricketbollen ovan)? Problemet med denna förklaring är att skruven skulle bero på hur bollen placeras på marken.
/Peter E 2006-08-17

Svar:
Hej Joakim! Intressant fråga till en entusiastisk golfare men dålig puttare!

Puttning är egentligen mycket enkelt: slå bollen med rätt hastighet i rätt riktning med hänsyntagande till fall på grund av greenens lutning och eventuell vind. Förutom en god teknik (som finslipas med mycket träning) är självförtroende A och O i golf: alla golfare vet att man misslyckas med de flesta slagen med en klubba man inte "tycker om".

Du har helt rätt i att det är mycket viktigt att få bollen att rulla - inte glida - så snart som möjligt. Detta gör man genom att sätta "överskruv" på bollen, dvs så att bollen roterar i samma riktning som den gör när den rullar. Detta är tvärtom mot skruven som åstadkoms med andra klubbor: klubbladets loft (lutningen mot horisontalplanet) orsakar underskruv, vilket en skicklig spelare kan utnyttja till sin fördel, se golfboll. Du vill alltså ha mycket lite loft på en putter (slagytan skall vara nästan 90 grader mot horisontalplanet), annars får du en i de flesta fall icke önskad underskruv.

Överskruven åstadkommes genom att man täffar bollen när puttern är lite "på uppgång" - bollen lite till vänster i stansen och en pendelrörelse hos klubbhuvudet som når sin lägsta punkt lite innan det träffar bollen. Det fordras lite träning för att lyckas med det varje gång.

Vilka egenskaper bör en bra putter ha?

• Det bör vara lätt att sikta
  
• Tydlig "sweetspot", vilket är den träffpunkt som inte orsakar rotation hos klubbhuvudet
  
• Lite loft (högst några få grader) så man kan åstadkomma överskruv
  
• Ett handtag som ger en känsla för vart klubbhuvudet pekar (ej cylindersymmetriskt)
  

Kan man med elementär fysik förstå varför man vill ha överskruv? Ja, jag tror det. Om man träffar bollen exakt på bakkanten med klubbhuvudet vinkelrätt mot och rörelseriktningen parallellt med den önskade riktningen (square hit), så kommer bollen att glida på underlaget till att börja med. Friktionen mot underlaget får bollen att börja rulla efter ett tag (c:a en meter). Från början har bollen endast rörelseenergi, men när den börjar rulla övergår rörelseenergin delvis i rotationsenergi, se fråga [14738]. Bollen saktar alltså in mycket i början av rörelsen. Pröva att slå några 10-metersputtar med samma svinghastighet dels genom att träffa bollen "square" och dels med överskruv. Du kommer att finna att puttarna med överskruv går betydligt längre än puttarna utan skruv. Dessutom blir längden mycket mer konsistent, och det är detta som gör att tekniken är att föredra. Titta på en god puttare (proffs), så skall du se att bollen rullar mycket snart efter träffen, medan bollen vid en dålig träff glider och hoppar vilket ger ett sämre resultat.

Friktionen (och därmed uppbromsningen) är större när bollen glider (och kanske hoppar) än om den rullar fint. Du får därför en mer konsistent putt med en rullande boll.

Kan man inte få överskruv med ett negativt loft på puttern? Nej, det fungerar antagligen inte eftersom man tvingar bollen nedåt in i greenen. Men kanske skulle man kunna pröva lite negativt loft? Såvitt jag vet finns inga sådana putters, och om det fungerade skulle det säkert finnas det.

En sak är i varje fall säker: om du kan konstruera en putter som gör puttningen lättare och dessutom övertyga golfare att den fungerar, så är du miljonär!

PS. Heter du verkligen Green? Då får du kalla puttern Green-putter!

PS2. Lycka till med puttertillverkningen!

Tillägg juni 2017:

Här är en putter med en speciell yta ("microhinges") som påstås ge bollen överskruv:





Se länk 1 för mer om puttning.
/Peter E 2006-10-14

Svar:
Sara! Tyngdkraften rakt nedåt, normalkraften vinkelrätt uppåt från backen, friktionkraften bakåt längst skidan och till slut luftmotståndet i en riktning motsatt färdriktningen.

Det var ett svar som frågan är formulerad. Men du menade antagligen vilken g-kraft en skidåkare kan utsättas för när hon svänger. Accelerationen a i en cirkelbana med radien r är

a = F/m = v²/r

där v är hastigheten. Låt oss anta hastigheten för en störtloppsåkare är 100 km/tim och krökningsradien r 50 m. Hastigheten 100 km/tim är 100000/3600 = 28 m/s, så vi får

a = 28²/50 = 15.68 m/s² = (15.68/9.81) g = 1.60 g.

Denna g-kraft är alltså riktad utåt, bort från krökningscentrum. Till denna komponent får man sedan addera tyngskraftkomponenten 1g riktad nedåt. Resultanten av dessa två blir då med hjälp av Pythagoras sats:

sqrt(11+1.61.6)g = 1.90g

Under korta perioder kan man nog tänka sig t.o.m. tvärare svängar än detta, så man kan förstå varför en störtloppsåkare är så trött efter bara ett par minuters åkning.
/Peter E 2009-02-18