Svar:
Anton! Kul leksak! Jag har inte sett den tidigare!

Apparaten (se videon nedan) består av en ränna, ett par starka magneter och några stålkulor.

Funktionen är lite relaterad till Newtons vagga, se fråga [11464] . Den fysikaliska grunden är, förutom magnetism, lagarna om energins och rörelsemängdens bevarande.

Skillnaden jämfört med Newtons vagga är att den högra kulan (vi refererar nu till bilden nedan) kommer att accelereras mot magnet/stålkule paketet av magneten. Detta innebär att rörelsemängd överföres från den rörliga kulan till det från början stationära paketet kulor/magneter medan kulan rör sig från höger till vänster. I fallet Newtons vagga accelereras den fria kulan av tyngdkraften och ger alltså ingen rörelemängdsöverföring till de stationära kulorna före kollisionen.

Magneten behövs alltså för att sätta fart på den högra kulan. Den behövs även för att hålla ihop paketet av kulorna till vänster. Dessa behövs för att ge en stor massa på den från början stationära biten. Ett ytterligare skäl för att ha mer än en stationär kula är att den vänstraste kulan (som flyger iväg) inte får sitta alltför hårt fast. Om den gjorde det skulle den inte kunna flyga iväg.

Detta är vad som sker:

1 Den högra kulan rör sig långsamt mot magneterna.

2 När kulan närmar sig magneterna accelereras den mer och mer mot magneterna. För att bevara rörelsemängden kommer de stationära kulorna och magneterna att röra sig lite åt höger.

3 Den högra kulan kolliderar med magneten. Stöten fortplantas genom magneterna och de stationära kulorna.

4 Av samma skäl som för Newtons vagga blir det kulan längst till vänster som tar upp den rörelsemängd som den högra kulan hade vid kollisionen.

5 Lägg märke till att "restpaketet" rör sig lite åt höger efter stöten (till skillnad från Newtons vagga). Anledningen är att kraften som accelererade den högra kulan kom från det från början stationära paketet.

"Gauss gun" kan även vara en pistol med ferromagnetisk kula som accelereras med hjälp av varierande magnetfält i ett antal spolar, se Coilgun. Detta är alltså någonting helt annat och mycket farligare än vad som beskrivs ovan.

Anledningen till benämningen "Gauss pistol" är naturligtvis att magnetfält är involverade. Se även länk 1.


/Peter E 2009-02-26

Svar:
Johanna! Karusellen ser ut som den på bilden nedan från Chair-O-Planes.

För att sitsarna med (eller utan) passagerare skall röra sig i en cirkelbana erfordras en kraft riktad mot centrum. Denna s.k. centripetalkraft ges av

F_r = mv²/r

Om rotationshastigheten v ökar ökar radien r och vinkeln a mellan vertikalplanet och kättingen minskar för att centripetalkraften skall öka, se figuren nedan.

Det är två krafter som tillsammans orsakar nettokraften F_r (de två steckade krafterna i figuren):

1 Spänningen i upphängningskedjan F_F riktad snett uppåt i kedjans riktning.

2 Tyngdkraften F_G = mg riktad rakt nedåt.

Från triangeln med F_F och F_r får man

tan a = F_r/F_G

dvs

F_r = tanaF_G = tanamg

Men enligt ovan var ju

F_r = mv²/r

dvs

mv²/r = tanamg

eller

v² = rtanag

Vi ser för det första att sambandet inte beror av massan m.

Om avstÃ¥ndet frÃ¥n rotationscentrum till upphängningspunken är r₀ blir radien

r = r₀ + lsina

där l är kedjans längd. Vi får alltså till slut sambandet

v² = (r₀ + lsina)tanag

Vi ser att om hastigheten v ökar så måste även vinkeln a öka. Ekvationen ovan är svår att lösa exakt, men i appleten under länk 2 kan man variera parametrarna och se vad som händer.

Se Slagkraft - Naturvetenskap på Liseberg för mer om Kättingflygaren och andra Liseberg-attraktioner.

Se även Kättingflygare.

/Peter E 2009-03-09

Svar:
Tobias! Egentligen inte en fråga, men en intressant diskussion. Jag antar att du refererar till svaret på fråga [10672].

Du ger ingen referens till ditt påstående och din förklaring att ett statiskt undertryck skapat av vattnets avdunstning är huvudförklaringen är inte tillräcklig vad gäller höga träd! Att kapillärkraften i detta sammanhang är försumbar är vi överens om. Det finns flera artiklar om problemet, men de är antingen obegripliga eller felaktiga. En av de bättre jag hittat är länk 1, som även beskriver demonstrationsexperiment som är relativt lätta att utföra. Förklaringen i länk 2 duger bara för träd under 10m.

Atmosfärstrycket är 1.01310⁵ Pa. Detta motsvarar trycket av en vattenpelare av höjden x. Vi har att

1.01310⁵ = xrg
= x1000[kg/m³] 9.81[m/s²]

dvs

x = 1.01310⁵/(10009.81) = 10.3m

Detta betyder att även om man pumpar fullständigt vakuum ovanför en vattenpelare så kan den aldrig bli högre än 10m. Om vi dessutom tar hänsyn till att vattnet längst upp kommer att koka och ge upphov till ett ångtryck, blir den längsta möjliga sammanhängande vattenpelaren t.o.m. lite under 10m.

De som sett en klassisk kvicksilverbarometer med vilken man mäter lufttrycket genom att mäta höjden på en kvicksilverpelare känner igen problemet. Enda skillnaden är att normallängden på grund av kvicksilvrets höga densitet är 760mm i stället för vattenpelarens 10m.

Med hjälp av osmos-kalkylatorn i Osmotic Pressure Calculation kan man lätt konstatera att även helt rimliga koncentrationsskillnader ger upphov till tryck pÃ¥ flera atmosfärer. En lösning av vatten med 50g glukos (C₆H₁₂O₈, molekylvikt 212) med volymen 1 liter ger t.ex. ett osmotiskt tryck pÃ¥ nästan 6 atmosfärer vilket motsvarar en vattenpelare pÃ¥ 60m. Det är alltsÃ¥ ingen svÃ¥righet att förklara transport av vatten i ett 100m högt träd.

Låt oss först se hur man skulle kunna pumpa vatten från en brunn som är 15m djup. Antingen delar man upp transporten i två etapper som vardera är mindre än 10m eller också placerar man pumpen nere i brunnen. I det senare fallet skapar pumpen ett övertryck som i princip kan pumpa vattnet hur långt som helst.

Hur har då naturen löst problemet för höga träd? Jag vill påstå att man inte riktigt vet detta, eftersom de förklaringar jag hittat strider mot fysikaliska lagar. Jag tror att detta är hur det går till:

I cellerna i roten finns det något löst ämne (kan vara salter eller socker) som skapar ett osmotiskt tryck mot det omgivande vattnet. Vattenmolekyler kommer då att vandra utifrån och in i roten för att jämna ut koncentrationen på båda sidor om det halvgenomsläppliga membranet - observera att det lösta ämnet i roten kan inte komma ut genom membranet. Volymen vatten i roten ökar då (se nedanstående figur), och om roten/transportröret utformas på rätt sätt (som en termometer tjock nedtill och smalare upptill) kan man få en mycket hög vattenpelare. Höjden på vattenpelaren motsvarar skillnaden i osmotiskt tryck innanför och utanför roten.

Än så länge har vi ett statiskt system - vi har en hög vattenpelare men ingen transport av vatten. Det är här undertrycket som skapas av avdunstningen kommer in. Avdunstningen skapar ett undertryck som är tillräckligt för att suga upp vattnet den sista biten. Avdunstningen skulle alltså skapa en uppåtgående vattenström. Eftersom de i roten lösta molekylerna transporteras bort, så måste de hela tiden förnyas i roten. Detta kostar en del energi, men det är det pris växten måste betala för vattentransporten som naturligtvis kräver energi.

Se den vidare diskussionen i fråga [16040].

/Peter E 2009-03-12

Svar:
Ljuset följer den snabbaste vägen som i ett gravitationsfält inte är en rät linje, se fråga [17427].

Det är ingalunda trivialt att räkna ut avböjningen. Man måste använda hela formalismen för den allmänna relativitetsteorin, se Two-body_problem_in_general_relativityApproximate_formula_for_the_bending_of_light.

Avböjningen vid solranden ges av uttrycket

df = 4GM/c²b

där G är gravitationskonstanten G = 6.674 10^-11 m³s^-2kg^-1

M är solens massa M = 1.989 10³⁰ kg

c är ljushastigheten c = 2.998 10⁸ m/s

b är solens radie b = 6.955 10⁸ m

Låt oss innan vi räknar ut df se vad den har för dimension

[df] = [m³s^-2kg^-1][kg]/([m²/s²][m]) = 1

dvs dimensionslöst som sig bör för en vinkel i radianer.

Vi får

df = 8.494 10^-6 radianer

Men 1 bågsekund är

2p/(3606060) = 4.848 10^-6 radianer.

Avböjningen i bågsekunder blir alltså

df = (8.494 10^-6)/(4.848 10^-6) = 1.75"

För att räkna på ett annat objekt, t.ex. ett svart hål, byter man bara ut massan M och radien b i formeln ovan.

Eddingtons mätningar vid solförmörkelsen 1919, nedanstående bild, (se Tests_of_general_relativity och länk 1) har ifrågasatts, men resultatet av mätningen har senare bekräftats. I vilket fall som helst innebar mätningarna en omedelbar acceptans av den allmänna relativitetsteorin från alla utom möjligen nobelpris-kommitteen.

/Peter E 2009-03-23

Svar:
Matilda! Nationalencyklopedin definierar friktion som

"motstånd mot glidning mellan två föremål i kontakt. Friktionskraften är riktad motsatt glidningen, normalt lika med friktionskoefficienten gånger den sammanpressande kraften mellan föremålen och oberoende av kontaktytans storlek och av glidfarten. Friktion orsakas av kraftverkan mellan atomer i ytskikten hos föremålen och studeras inom tribologi. Friktion är till nytta (minskar halka, t.ex. mellan bildäck och vägbana), men medför förluster i tillgänglig energi när högvärdig rörelseenergi omvandlas till värme (friktionsförluster)."

Wikipedia säger:

Friktion eller gnidningsmotstånd har att göra med hur ytan på materialet är beskaffad. En slät och jämn yta som på is ger mindre friktion än en skrovlig och knottrig yta som på betong. Det beror helt enkelt på att utsprång på den ena kroppen tar i fördjupningar på den andra, så att det behövs extra kraft för att få dem loss igen. De elektromagnetiska krafterna mellan atomer spelar emellertid också en betydande roll. När två kroppar är i nära kontakt håller atomerna fast vid varandra och verkar då i motsatt riktning mot rörelsen. På så sätt omvandlas kinetisk energi (rörelseenergi) till värme. (Friktion)

Om friktion är bra eller dålig? Jag antar du menar om vi har nytta av den eller tvärtom. Om inte friktionen funnits hade du inte kunnat gå, du hade ramlat omkull hela tiden. Å andra sidan hade bilar dragit mindre bensin - men inte kommit någonstans! Så det är nog väl att friktion finns :-)!

Man kan efter behov öka friktionen - för bilar med dubbdäck och sandning av vägar - eller minska friktionen - med olja i en bilmotor. Dessa åtgärder ändrar friktionskoefficienten. Man kan även öka friktionen genom att öka normalkraften, t.ex. med vingar eller spoilers på en formel 1 bil (downforce).

Se fler frågor om friktion under nedanstående länk. Se även Friktion och Friction. Se fråga [14921] för begreppet friktionskoefficient.

/Peter E 2009-03-23

Svar:
Susanna! Låt oss först beräkna accelerationen a = dv/dt. Hastigheten v ges av din ekvation (1). Derivatan av v med avseende på tiden t blir då

a = dv/dt = 10-5t

Anledningen till att accelerationen skrivs sÃ¥ här är ju att allteftersom löparens hastighet ökar, sÃ¥ mÃ¥ste accelerationen minska¹. Vi kan se att accelerationen enligt ovanstÃ¥ende modell är 0 vid t=2s. DÃ¥ har löparen alltsÃ¥ uppnÃ¥tt sin sluthastighet. Om vi sätter in t=2s i (1) fÃ¥r vi slut(max)hastigheten 10 m/s.

Definitionen på hastighet är v=ds/dt. Hastigheten är alltså tidsderivatan vid en viss tidpunkt av den tillryggalagda sträckan. Se det så här: på den lilla tiden dt rör sig löparen sträckan ds. Hastighet är sträcka per tidsenhet alltså ds/dt.

Om vi våldför oss lite på matematiken kan vi se att ds=vdt. Hastigheten v ges ju som funktion av t av (1). Vi kan då beräkna v for en massa värden från 0 till 2s och multiplicera med dt. Dessa ds kan vi sedan summera för att få den sträcka löparen tillryggalagt.

Matematiken bakom ovanstående kallas Infinitesimalkalkyl och utvecklades av Newton och Leibniz på 1600-talet (se Calculus och fråga 16084 nedan). Formellt är ds/dt något som kallas derivata. För att beräkna s från funktionen ds/dt måste vi integrera. Det finns massor med regler för derivering och integration (som man får lära sig i matematiken), men det viktiga i detta sammanhang är att integration är omvändningen till derivering. Så om vi integrerar ds/dt med avseende på tiden så får vi sträckan s.

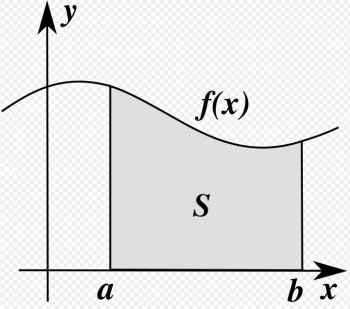
Bilden nedan från Wikimedia Commons visar att integralen helt enkelt är ytan S under en funktion f(x). Integralen är alltså en yta, och räknas ut som en oändlig summa av pyttesmala rektanglar.

Hur får man då fram funktionen (2) från (1)? Ja, man måste kunna lite integreringsregler. Oftast är det emellertid enklare att derivera än att integrera, så låt oss kontrollera om (1) är derivatan av (2):

(d/dt)(5t²-2.5t³/3+C) =
10t-2.5t²

vilket alltså stämmer bra.

Det är naturligtvis måttligt intressant att beräkna hur en hundrameterslöpare spinger, men exemplet vill visa hur man i fysiken arbetar med matematiska modeller som sedan kan jämföras med verkligheten. Här är till sist en tabell med värden på a, v och s beräknade med ovanstående uttryck och med antagandet att löparen från 2 sekunder och framåt har den konstanta hastigheten 10 m/s.

 t a v s

-------------------------

 0 10 0 0

 1 5 7.5 4.2

 2 0 10 13.3 3 0 10 23.3

 4 0 10 33.3

 5 0 10 43.3

 6 0 10 53.3 7 0 10 63.3

 8 0 10 73.3

 9 0 10 83.3

 10 0 10 93.3

 11 0 10 103.3

Vi ser alltså att löparen springer 100m på mellan 10 och 11s, dvs god svensk klass men ingen Usain Bolt :-)!

Hoppas detta hjälpte dig något!

¹ Till skillnad frÃ¥n en raket som accelererar snabbare och snabbare. Skillnaden beror pÃ¥ att för raketen är den största delen av massan bränsle, och detta försvinner ju efter hand som raketen accelererar.

/Peter E 2009-04-17

Svar:
Hur mycket du väger beror på tyngdaccelerationen g (tyngdkraften blir mg där m är din massa). Tyngdaccelerationen ges enligt fråga [15114] av

g = (M G)/R²

där G är Newtons universella gravitationskonstant, M är planetens massa och R är dess radie. Tyngdaccelerationen ökar alltså med ökande massa M och minskar med ökande radie R. Massor och radier för planeter kan du hitta i Planetary Fact Sheets.

Låt oss räkna ut g på "ytan" av Jupiter:

Jupiters massa M: 189810²⁴ kg

Jupiters radie R: 7010⁶ m

Gravitationskonstanten G: 6.6710^-11 m³/ (kg s²)

g(Jupiter) = (M G)/R² = 26 m/s²

alltså c:a 2.5 gånger jordens.

Se länk 1 för tyngaccelerationen hos fler objekt.

Vi kan skriva om ovanstående uttryck som

g = RGM/R³.

Eftersom medeldensiteten r är proportionell mot M/R³ blir g proportionellt mot

RGr

Större radie ger alltså större g för konstant medeldensitet.

Sedan är det en annan sak att allt detta är ganska teoretiskt för en gas-planet. Eftersom det inte finns någon fast yta har du inget att stå på, så du befinner dig i fritt fall (bortsett från luftmotståndet).
/Peter E 2009-10-07

Svar:
Kerstin! Det beror på bollens och golvets egenskaper om snurr-riktningen ändras. Om friktionen boll-golv är stor kan rotationsriktningen säkert ändras.

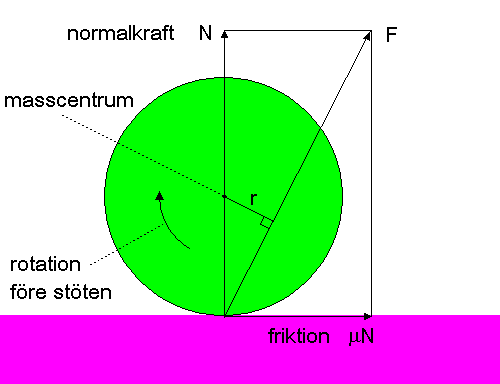
Se nedanstående figur. Bollen roterar på nervägen medurs. Vi har en normalkraft vinkelrätt mot golvet och en friktionskraft parallellt med golvet och motriktad rotationen. Vi kallar resultanten till dessa två krafter för F. Eftersom F inte går genom masscentrum skapar F ett rotationsmoment Fr. Detta är motriktat den urspungliga rotationen. Om rotationsmomentet är tillräckligt stort (dvs friktionen är tillräckligt stor) kommer det att orsaka att bollens rotation vänder.

Detta är en mycket idealiserad bild - i verkligheten måste man ta hänsyn till att bollen deformeras och att en del av rörelseenergin av inre friktion förvandlas till värme.

/Peter E 2009-10-19

Svar:
Marianne! Vid tillräckligt högt tryck går säkert burken sönder. Detta är ingen myt. Låt oss titta på vad som händer med trycket.

Om det bara finns gas i burken (dvs burken är nästan tom) kan man tillämpa allmänna gaslagen (gaslagen, allmänna, Ideala_gaslagen):

pV = nRT

(p tryck i Pa, V volym i m³, n antal mol gas, R gaskonstanten 8.314 J/(molK), T absoluta temperaturen i K)

Trycket ökar alltså med absoluta temperaturen för konstant volym. Om vi utgår från 20 grader som normaltemperatur så ökar trycket vid 50 grader med faktorn (50+273)/(20+273) = 1.10, alltså med 10%. Vi måste gå till över 300 grader för att trycket skall fördubblas. Så om burken innehåller en ideal gas (allt i burken är i gasform) är det ingen fara, eftersom burken bör tåla ganska höga temperaturer.

Men en sprayburk innehåller emellertid inte bara gas utan även vätska. I en genomskinlig behållare (t.ex. en cigarrettändare, se fråga 16119 nedan) kan man se detta. Om man skakar en spayflaska försiktigt, kan man känna att en vätska "skvalpar omkring" inne i burken. Problemet är då inte lösbart med antagandet om en ideal gas, utan man måste ta hänsyn till vätskans Ångtryck.

Ångtrycket är relaterat till vätskans kokpunkt - kokpunkten vid 1 atmosfärs tryck är den temperatur vid vilken vätskans ångtryck är 1 atm. Bilden nedan från Wikimedia Commons visar ångtrycket för några vätskor som funktion av temperaturen. De olika ämnena i figuren uppför sig ganska lika, med skillnaden att kokpunkten är mycket olika. Om vi tar neo-Pentan (mörkgrön kurva) som exempel ser vi för det första att kokpunkten vi trycket 1 atm är 10 grader. För några olika temperaturer kan vi läsa av följande från kurvan:

10^oC - 1 atm

20^oC - 1.4 atm

50^oC - 3.5 atm

80^oC - 8 atm

Vi ser alltså att trycket ökar mycket med förhöjd temperatur.

Vad kan vi dra för slutsatser? För det första att Mythbusters test visade att tillverkarnas rekommenderade högsta temperatur var konservativt säker. Det framgår inte hur högt upp i temperatur man gick vid testen. För det andra kan man dra slutsatsen att om burken bara innehåller gas, så tål den ganska höga temperaturer. Om burken emellertid även innehåller vätska ökar trycket mycket snabbt med temperaturen, så burken kommer till slut att explodera.

/Peter E 2009-10-22

Svar:
Alida! Det är mycket omfattande frågor du ställer och de är delvis mer teknologi än fysik. Jag kommer att behandla några av de fysikaliska aspekterna i din fråga.

Förbränningsmotorer

Bilens bränsle förbränns tillsammans med syre från luften i en cylinder. Varm gas tar mer plats än kall gas och expansionen driver en kolv. Via en vevaxel omvandlar man fram-och-tillbaka rörelsen till rotation som kan driva hjulen, se nedanstående animering från Wikimedia Commons (Engine). Observera att det är inte den höga temperaturen i sig som driver förbränningsmotorn utan skillnaden i temperatur mellan de varma och kalla delarna. En förbränningsmotor måste alltså alltid kylas - oftast med vatten. I ett kraftverk eller fabrik kan man använda kylvattnet för uppvärmning, men i en bil är det varma kylvattnet en ren energiförlust. Effektiviteten (verkningsgraden) för en förbränningsmotor (producerat mekaniskt arbete/(bränslets energiutveckling) är av storleksordningen 40% (Internal_combustion_engine).

Bromsar

Den traditionella konstruktionen för bromsar är två plattor eller cylindrar som bringas i kontakt och genom friktion förvandlar mekanisk energi till värme. Normalt är denna värme en ren förlust.

Det finns emellertid bromsar som återanvänder bromsenergin.

Om bilen drivs av en elmotor och batterier kan man använda motorn som broms. Elmotorn blir i stället en generator som producerar ström som laddar patterierna. Det är alltså det mekaniska motståndet från generatorn (Lenz's_law) som ger bromsverkan. En stor del av energin kommer till nytta från det uppladdade batteriet. Se Regenerative_brakeThe_motor_as_a_generator.

En annan lösning är att använda sig av ett svänghjul. Ett svänghjul (se Flywheel) är en mekanisk anordning vars syfte är att lagra rörelseenergi genom att en tung cylinder sätts i rotation. För ett fordon överför man rörelseenergi till rotationsenergi hos svänghjulet. Denna rotationsenergi kan sedan återanvändas för acceleration. Systemet används bland annat av några stall i Formel 1. Systemet kallas KERS (Regenerative_brakeKinetic_Energy_Recovery_Systems). Man kan med detta system få några extra hästkrafter för en snabb omkörning. Svänghjulet laddas alltså upp av uppbromsningarna. Anledningen till att inte alla Formel 1 stall använder KERS är att systemet är ganska tungt (c:a 25 kg) och därför medför begränsningar i den optimala viktfördelningen i bilen. (Kommentar: Systemet var förbjudet under säsongen 2010, men är tillåtet från säsongen 2011.)

Hydraulik/servosystem

Hydraulik är ett system med två kolvar med olika diameter som är förbundna med en slang innehållande en vätska, vanligen olja. Vätskan är inkompressibel (kan inte tryckas ihop), och man skapar ett övertryck genom att trampa på en pedal. Om kolvarnas ytor förhåller sig som 1/10 får man en förstärkning av kraften med en faktor 10. På samma sätt som för en hävstång betalar man kraftförstärkningen med att den mindre kraften verkar över en längre sträcka, se Hydraulik.

Ett servo-system skall enligt en strikt definition (Servomechanism) även innehålla en extern drivkälla (t.ex. vakuum från motorn) och återkoppling.

/Peter E 2009-10-27