Vill du ha ett snabbt svar - sök i databasen
Nyckelord: centrifugalkraft
6 träffar
Finns centrifugalkraften. Om den inte finns vill jag ha en förklaring. Tack!
1997-01-20
För att svara på din fråga så måste vi utreda vad en kraft är. Kroppar påverkar varandra, jorden attraherar till exempel en sten, stolen som Du sitter påtrycker på Dig, magneten drar i ett järnstycke. Krafter används för att
beskriva sådan mekanisk påverkan.
Då kommer vi till en filosofisk fråga: Finns krafter? Mitt svar är nog
att krafter inte finns i naturen utan endast i vår beskrivning av naturen.
Nu till centrifugalkraften. Om Du åker karusell så kan vi beskriva Din rörelse på två sätt: Dels att Du rör Dig i en cirkel och dels att Du sitter still i karusellen.Om vi väljer det senare synsättet så måste vi införa en ny typ av krafter, så kallade tröghetskrafter. Centrifugalkraften är en sådan kraft.
Svaret på Din fråga är: Egentligen finns inga krafter utan vi måste själva införa dem i fysiken och vi kan även införa centrifugalkraften om vi så vill!
/GO 1998-11-06
Vår fysiklärare säger att centrifugalkraften inte är en reell kraft, utan bara teoretisk. Betyder det att man inte kan använda den i beräkningar? Skulle vara tacksam om ni kan reda ut begreppen.
1997-03-20
För att reda ut detta så börjar vi från början:
Vad är en kraft? Jag brukar lite tillspetsat säga
att “Krafter finns inte“. Vad som vi ser i naturen
är att olika kroppar påverkar varandra: Vi sparkar
iväg en fotboll, vi stänger en dörr, två magneter attraherar varandra,
jorden accelererar simhopparen som faller osv. Allt detta är exempel
på mekanisk påverkan av en kropp på en annan.
För att beskriva denna mekaniska påverkan inför man i fysiken kraftbegreppet.
Alla krafter är alltså “bara teoretiska“. Krafter finns alltså bara
i den fysikaliska teorin (eller modellen om du så vill). När en
kropp påverkas av en annan kropp, vilket vi beskriver med en kraft
så deformeras eller accelereras kroppen. Ofta sker naturligtvis
bägge sakerna samtidigt. Tänk på en tennisboll som slås iväg med
ett racket. För att beräkna accelerationen använder man Newtons lag:
F =ma. En fråga som då genast uppstår är: Relativt vilket system
ska accelerationen beräknas?
Fundera: En kropp ligger still på jorden. Ligger den
still i förhållande till solen? Det är väldigt svårt att säga vad
som "ligger still". För att Newtons accelerationslag ska gälla måste
accelerationen beräknas i förhållande till ett system som "ligger stilla".
Men ibland tycker man det är lämpligt att säga att en kropp rör sig relativt
något som inte "ligger stilla". Tänk på en karusell.
Du sitter still i karusellen och vill räkna ut de krafter som verkar på dig.
Man kan då "låtsas" att Newtons kraftlag gäller även om din rörelse
relateras till den roterande karusellen, men man måste då införa en ny typ av
krafter nämligen tröghetskrafter. Centrifugalkraften är en sådan tröghetskraft.
Dessa krafter beskriver inte påverkan mellan kroppar på samma sätt som
"riktiga krafter". Använder man tröghetskrafterna korrekt så ger det
precis samma resultat som om man endast räknar med "vanliga" krafter.
Varning! Det är en stor risk att man blandar ihop vanliga krafter med
tröghetskrafter och jag tycker nog att man i de flesta fall bör hålla sig
till de vanliga krafterna. Men det finns några problemställningar där
tröghetskrafter är naturliga.
Problem: Som ett test på om du kan använda
tröghetskrafter korrekt får du här ett problem. Vad skulle
tyngdaccelerationen vara vid ekvatorn om jorden inte
roterade? Räkna ut detta både med och utan tröghetskrafter!
2000-03-31
Varför orsakar månen två tidvattensbulor?
Att det blir flod på den sidan av jorden som är vänd mot månen pga dess dragningskraft är väl förhoppningsvis rätt uppfattat. Men samtidigt blir det ju flod på andra sidan av vårt kära klot, alltså den sidan som är vänd bort från månen. Förklaras det också utav månens dragningskraft?
/Hans F, Kvarnbyskolan, Mölndal 1999-05-20
Låt oss börja med att definiera tidvatten:
Problemet med de två bulorna är en klassisk besvärlig fråga eftersom man använder två till synes olika modeller som förklaring. Mer om detta nedan; här är först den förklaring jag föredrar från den engelska versionen av Wikipedia,
Titta på den översta bilden. En partikel på jordytan närmast månen påverkas av en kraft som är lite större än en kraften på en partikel i centrum, som i sin tur påverkas av en större kraft än en partikel på frånsidan eftersom gravitationskraften avtar som 1/r2. I stället för krafter kan vi uppfatta pilarna som accelerationer som orsakas på en massa m (F=ma). Om vi subtraherar accelerationen i jordens masscentrum får vi kvar accelerationer enligt den nedre figuren: på närsidan en liten rest riktad mot månen och på bortre sidan en rest riktad från månen. Denna subtraktion innebär att vi väljer ett koordinatsystem som är i vila i förhållande till jordens masscentrum.
Låt oss föreställa oss jorden med hav överallt. De resulterande krafterna kommer då att lyfta havet med ett litet belopp h så att mgh (m är massan av, säg, en cm3 vatten) är lika med den resulterande tidvattenskraften. Höjden h är c:a 0.54 m och, om man även tar med solens maximala påverkan, 0.79 m. När väl denna justering av havsytans form skett, råder jämvikt och jordens form är fix.
Tidvatten kan emellertid på vissa platser vara upp till 10 m. Anledningen till denna stora avvikelse är att jorden bara delvis är täckt av hav och att kustlinjerna kan ge en stor förstärkning av effekten, se Lectures on tides
Om det inte fanns något vatten på jorden skulle jordens form ändå anpassa formen efter tidvattenskrafterna, men mindre eftersom fast material gör större mekaniskt motstånd.
Figuren i mitten nedan visar vad som händer i en godtycklig punkt A på havsytan. Eftersom avståndet MA' är större än MA kommer kraften i A vara större än kraften i A' (nedre triangeln). Vi får alltså i detta fall en resulterande kraft riktad uppåt till höger.
Motsvarande beräkning för hela klotet ger resultatet i den nedre figuren. De resulterande krafterna kommer att deformera klotet så att vi får en rotationsellipsoid med storaxeln riktad mot månen. Observera att de resulterande krafterna finns på den odeformerade jorden. När vattnet anpassat sig kommer den extra höjden på vattenpelaren att kompensera kraften och vi har jämvikt.
Vi har här bortsett från jordens rotation. Om man även tar hänsyn till denna och friktionen kommer ellipsoiden att vridas, se fråga [13056].
Experiment med resonans
Ta en balja eller en spann och fyll i vatten till några centimeters djup. Skaka baljan fram och tillbaka med jämn rytm. Pröva med olika rytmer. Vid vissa skakningsrytmer blir det bara små vågeffekter. Vid andra rytmer blir vågorna bara större och större, så att det till slut skvalpar ut. Det fenomenet kallar vi resonans.
Diskussion av till synes olika förklaringar
En del förklaringar till tidvattenseffekten involverar centrifugalkraften, t.ex. The Cause of Tides (easy version)
Anledningen till skillnaden är vilket koordinatsystem man föredrar. Ovan har vi föredragit jordens masscentrum. I detta har vi ingen acceleration (vi står förhoppningsvis stadigt på jordytan) och deformationen orsakas av skillnaden i gravitation i olika punkter på jorden.
Om vi i stället betraktar systemet jorden-månen från deras gemensamma masscentrum (som ligger c:a 1/4 jordradie under jordytan), så accelereras jorden hela tiden (roterar kring masscentret), och vi måste ta hänsyn till centrifugalkraften.
Observera är deformationen inte uppkommer bara vid rotationsrörelse, utan jorden skulle vara en ellipsoid även om den föll fritt mot månen, se
Se även Tidvatten
 och länk 1 och 2.
och länk 1 och 2.
Hur skall man dosera vägen i en kurva?
Håller på med centralrörelse och tyckte då att det skulle vara kul att räkna lite på vilka farter som är möjliga i en doserad kurva utan att bilen får sladd. Gjorde en hel del förenklingar. Införde följande krafter tyngdkraften och normalkraften och en friktionskraft mellan vägbanan och däcken. Friktionskraften bör väll vara riktad innåt i kurvan men längs vägbanan? Friktionskraften får då en vertikal komposant som är riktad neråt och alltså samverkar med tyngdkraften, vilket känns lite märkligt. Kan det vara så? Hur löser man den här typen av problem?
/Marianne A, Ehrensvärdska, Karlskrona 2006-09-19
Marianne! Att räkna med friktion är ganska besvärligt eftersom det är svårt att veta vad friktionskoefficienten är. Det väsentliga i ditt problem är väl ändå doseringen, dvs vägens lutning i en kurva. Låt oss först definiera några storheter.
bilens massa = m
tyngdaccelerationen = g
normalkraften = N
doseringsvinkel = a
bilens hastighet = v
kurvradie = r
Bilen påverkas av två krafter: normalkraften N från vägbanan och mg från tyngdkraften. Om vi sätter samman dessa får vi en resulterande horisontell kraft R mot vägens krökningscentrum. Det är denna kraft som ger den acceleration som får bilen att röra sig med en cirkelbana. Accelerationen är
mv2/r = R = mgtana
Vi får alltså sambandet
v2 = rgtana
För en viss given hastighet och kurvradie kan vi alltså med detta uttryck beräkna den optimala doseringsvinkeln. Bilen kan naturligtvis även ta kurvan med en annan hastighet, men då behöver vi
Vi har, eftersom vi betraktar bilen från vägens perspektiv, inte infört någon

Hur mycket påverkas lodlinjens rikning av den centrifugalkraft som jordrotationen ger upphov till?
Om man står på marken bör man se till att hålla sin egen tyngdpunkt på en linje genom jordens tyngdpunkt och sina egna fötter, annars trillar man ikull. Men, hur muycket påverkar den centrifugalkraft som jordrotationen ger upphov till detta? Inte alls om man står på ekvatorn eller nord(syd)polen. Men i Skåne! Hur många grader (eller fraktioner av en grad) måste man luta sig "inåt" (dvs mot norr) för att inte falla ikull pga centrifugalkraften?
/Jon L, 2006-11-03
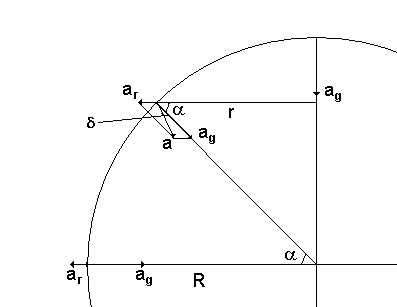
Jon! Det är en helt omärkbar effekt och det är knappast någon risk att man trillar, men låt oss som en övning räkna ut hur stor effekten är. Vi antar att jorden är klotformad och homogen med radien R. Den enda effekt vi tar hänsyn till är jordens rotation, vi bortser alltså från tillplattningen. Vi inför några beteckningar (se figuren):
ag = 9.822 m/s2 tyngdaccelerationen från jordens dragningskraft, se länk 1
ar accelerationen pga jordens rotation
a den resulterande tyngdaccelerationen
R = 6.37106 m jordradien
a latituden
w = 2p/(246060) = 72.710-6 s-1 vinkelhastigheten för jordens rotation
Vid polerna och ekvatorn är det ingen avvikelse i vinkel mellan a och ag (precis som du säger) medan det för medelhöga latituder är en avvikelse så att det är en liten "uppförsbacke" när man går norrut. Om du så vill kan du förstå detta som att "centrifugalkraften" försöker hindra dig att gå närmare rotationsaxeln.
Låt oss börja med att se vad som händer vid ekvatorn. Rotationshastigheten ges av
v = Rw = 6.3710672.710-6 = 463 m/s
Accelerationen pga rotationen blir
ar = v2/R = Rw2 = 6.37106(72.710-6)2 = 0.0337 m/s2
Tyngdaccelerationen vid ekvatorn blir alltså
ag - ar = 9.822 - 0.0337 = 9.788 m/s2
Accelerationen pga rotationen vid latituden a blir
ag = rw2 = Rcosaw2
Tillämpning av cosinuseoremet på triangeln ag, ar, a ger
a2 = ag2 + ar2 -2agarcos(a)
Den andra termen i högra ledet är mycket liten så vi kan försumma den. Vi får då
a = ag(1 - 2Rw2cos2a/ag)1/2 = ag(1 - Rw2cos2a/ag) =
ag(1 - 0.0337cos2a/9.822)
a = ag(1 - 0.00343cos2a)
Lodlinjens avvikelse från riktningen mot jordens medelpunkt d kan beräknas genom att vi tillämpar sinusteoremet på triangeln:
sind/ar = sina/a
sind = arsina/a =
Rw2cosasina/a =
Rw2sin2a/2a
Från detta uttryck kan vi se att avvikelsen är maximal för a=45o och noll för a=0o och a=90o.
Eftersom a är approximativt lika med ag och eftersom vinkeln är liten (sind = d) får vi
d = Rw2sin2a/2ag =
0.0337sin2a/(29.822) =
0.00172sin2a
d i grader blir
d = 1800.00172sin2a/p =
0.0985sin2a grader
Från detta kan vi se att lodlinjens maximala avvikelse (vid latituden 45o) är c:a 0.1o.
Varför flyger man utåt om man åker fortare i en karusell som ser ut som Kättingflygaren på Gröna Lund?
Varför flyger man utåt om man åker fortare i en karusell som ser ut som Kättingflygaren på Gröna Lund?
/Johanna 2009-03-09
Johanna! Karusellen ser ut som den på bilden nedan från
För att sitsarna med (eller utan) passagerare skall röra sig i en cirkelbana erfordras en kraft riktad mot centrum. Denna s.k. centripetalkraft ges av
Fr = mv2/r
Om rotationshastigheten v ökar ökar radien r och vinkeln a mellan vertikalplanet och kättingen minskar för att centripetalkraften skall öka, se figuren nedan.
Det är två krafter som tillsammans orsakar nettokraften Fr (de två steckade krafterna i figuren):
1 Spänningen i upphängningskedjan FF riktad snett uppåt i kedjans riktning.
2 Tyngdkraften FG = mg riktad rakt nedåt.
Från triangeln med FF och Fr får man
tan a = Fr/FG
dvs
Fr = tanaFG = tanamg
Men enligt ovan var ju
Fr = mv2/r
dvs
mv2/r = tanamg
eller
v2 = rtanag
Vi ser för det första att sambandet inte beror av massan m.
Om avståndet från rotationscentrum till upphängningspunken är r0 blir radien
r = r0 + lsina
där l är kedjans längd. Vi får alltså till slut sambandet
v2 = (r0 + lsina)tanag
Vi ser att om hastigheten v ökar så måste även vinkeln a öka. Ekvationen ovan är svår att lösa exakt, men i appleten under länk 2 kan man variera parametrarna och se vad som händer.
Se Slagkraft - Naturvetenskap på Liseberg
Se även Kättingflygare
 .
.
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.
Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar

