Svar:
Gravitationen (av latin gravis = tung) eller tyngdkraften är en av universums fyra fundamentala krafter, se fråga [3716]. Det är den attraherande kraft som massor utsätter varandra för, och ger upphov till det som vi kallar massans tyngd.

Gravitationskraften på massan m utanför ett klot med massan M ges av
F=GmM/r², där r är avståndet till masscentrum. Gravitationen innanför klotets yta beror av massfördelningen, eftersom endast den del av klotets massa som ligger innanför r ger bidrag till attraktionen. Om jordens densitet är konstant (vilket den definitivt
inte är), så ges massan innanför r av M'=Mr³/R³,
där R är jordradien. Gravitationskraften under jordytan (r mindre än R) blir alltså: F=GmMr/R³.

Gravitationskraften vid jordens medelpunkt (r=0) blir alltså 0. Om man kunde borra ett hål rakt genom jorden (omöjligt eftersom det är mycket varmt i jordens centrum och materien är flytande) skulle man kunna falla rakt igenom jorden och komma ut (vända vid jordytan) på andra sidan - bortsett från luftmotståndet. Om vi bromsar fallet skulle vi kunna stanna i centrum och sväva i ett tyngdlöst tillstånd.

Figuren nedan visar den uppmätta densiteten i jordens inre (från seismiska vågor, se Structure_of_the_Earth) och den beräknade tyngdaccelerationen. För de inre delarna kan man se att tyngdaccelerationen är approximativt proportionell mot r, medan den för de yttre delarna är närmast konstant.

Se även fråga [19792].

/Peter Ekström 2002-10-10

Svar:
Gravitationskonstanten är en generell konstant, som är lika i hela universum
(så vitt vi vet).

Vad du säkert syftar på är tyngdaccelerationen, som varierar något
beroende på var man är på jorden. Det beror på:

1. Jorden är tillplattad.

2. Centrifugalkraften på grund av jordrotationen.

3. Tidvattenfenomen orsakade av sol och måne.

4. Lokala variationer på grund av geologiska förhållanden.

En formel som tar hänsyn till de två första punkterna (Tyngdacceleration) är:

g = g_o
( 1 + 0.0052884 sin²(b)
- 0.0000059 sin²(2b))

g_o = 9.78049 m/s²

b = latituden.

För Västervik får man då 9.81764 m/s².

Direkt uppmätta värden kan man få hos Sveriges geologiska undersökning, SGU, men då får man betala för det.
/KS/lpe 2000-01-17

Svar:
Låt oss först skissa bakgrunden. Från Tycho Brahes mycket exakta mätningar av planeten Mars' rörelse kunde Johannes Kepler få fram tre lagar för planeternas rörelser. Isaac Newton kunde senare förklara dessa rörelser med hjälp av en lag, gravitationslagen, och nyutvecklad matematik (differentialkalkyl).

Keplers första lag: Planetbanorna är ellipser med solen i den ena brännpunkten. (Se nedanstående figur.)

Keplers andra lag: Varje planet rör sig längs sin elliptiska bana med en sådan hastighet att en linje från planeten till solen ("radius vector") alltid sveper över en lika stor area på samma tid. (Se nedanstående figur.) Planeten rör sig alltså snabbare när den är nära solen än när den är längre ifrån.

Från sin gravitationslag kunde Newton härleda följande variant av Keplers tredje lag:



P är (sideriska) omloppstiden

a är halva storaxeln av banan

G är gravitationskonstanten

m₁ och m₂ är objektens massor

Gravitationskonstanten (Gravitational_constant) bestämdes först av Henry Cavendish år 1798 med hjälp av tunga metallkulor och en torsionsvåg. Det aktuella värdet är

G = 6.673 10^-11 m³s^-2kg^-1

Eftersom gravitationskonstanten är svår att mäta är den en av de sämst kända naturkonstanterna.

Om vi sätter in värdet på G och förenklar lite får vi

(m₁+m₂) =
(4p²/G) a³/P² =
5.916 10¹¹ a³/P²

Detta uttryck kan tillämpas på vilket system av två objekt som helst, till exempel Mars och Mars' månar Phobos och Deimos eller t.o.m på ett svart hål i vintergatans centrum (se fråga 6228). Låt oss först tillämpa det på systemet jorden-månen:

(m₁+m₂) = 5.916 10¹¹ (384400000)³/(27.32246060)² = 6.03 10²⁴ kg.

Observera att vi måste använda SI enheter genomgående, dvs meter och sekunder. Från läget av jorden-månens gemensamma tyngdpunkt kan man bestämma m₁/m₂ till 81.3, så jordens massa blir 5.96 10²⁴ kg.

Tillämpat på systemet jorden-solen får vi

(m₁+m₂) = 5.916 10¹¹ (149600000000)³/(365.24246060)² = 1.99 10³⁰ kg.

Eftersom jordens massa kan försummas blir detta solens massa.

För planeter som saknar månar får man mäta deras påverkan av andra planeter. På senare tid har man ju skickat rymdsonder till många planeter, och då kan man bestämma planetens massa från sondens acceleration i närheten av planeten.

Observera att vi även kan bestämma jordens massa med hjälp av tyngdaccererationen 9.81 m/s² och Newtons gravitationslag:

F = ma = (mM G)/r² dvs

M = a r²/G = 9.81 (6.38 10⁶)²/(6.673 10^-11) = 5.98 10²⁴ kg.

Det var denna överensstämmelse som övertygade Newton (och andra) att det var samma kraft som påverkar varje massa på jorden (äpplet :-)) som den kraft som styr solsystemet.

Se även: Kepler's_laws_of_planetary_motion (avancerad), Johannes Kepler: The Laws of Planetary Motion (lite lättare) och Newton's Law of Gravity.

Formelsamling i fysik är en lättillgänglig sammanställning av fysikaliska formler och konstanter. Fysikalisk_konstant och den engelska versionen Physical_constant ger värden på fysikaliska konstanter.

/Peter E 2004-01-24

Svar:
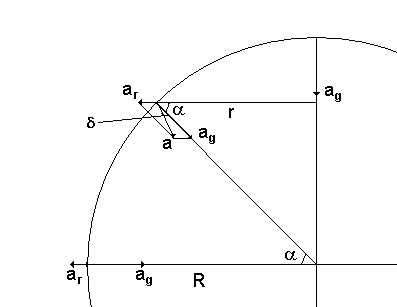
Jon! Det är en helt omärkbar effekt och det är knappast någon risk att man trillar, men låt oss som en övning räkna ut hur stor effekten är. Vi antar att jorden är klotformad och homogen med radien R. Den enda effekt vi tar hänsyn till är jordens rotation, vi bortser alltså från tillplattningen. Vi inför några beteckningar (se figuren):

a_g = 9.822 m/s² tyngdaccelerationen från jordens dragningskraft, se länk 1

a_r accelerationen pga jordens rotation

a den resulterande tyngdaccelerationen

R = 6.3710⁶ m jordradien

a latituden

w = 2p/(246060) = 72.710^-6 s^-1 vinkelhastigheten för jordens rotation

Vid polerna och ekvatorn är det ingen avvikelse i vinkel mellan a och a_g (precis som du säger) medan det för medelhöga latituder är en avvikelse så att det är en liten "uppförsbacke" när man går norrut. Om du så vill kan du förstå detta som att "centrifugalkraften" försöker hindra dig att gå närmare rotationsaxeln.

Låt oss börja med att se vad som händer vid ekvatorn. Rotationshastigheten ges av

v = Rw = 6.3710⁶72.710^-6 = 463 m/s

Accelerationen pga rotationen blir

a_r = v²/R = Rw² = 6.3710⁶(72.710^-6)² = 0.0337 m/s²

Tyngdaccelerationen vid ekvatorn blir alltså

a_g - a_r = 9.822 - 0.0337 = 9.788 m/s²

Accelerationen pga rotationen vid latituden a blir

a_g = rw² = Rcosaw²

Tillämpning av cosinuseoremet på triangeln a_g, a_r, a ger

a² = a_g² + a_r² -2a_ga_rcos(a)

Den andra termen i högra ledet är mycket liten så vi kan försumma den. Vi får då

a = a_g(1 - 2Rw²cos²a/a_g)^1/2 = a_g(1 - Rw²cos²a/a_g) =
a_g(1 - 0.0337cos²a/9.822)

a = a_g(1 - 0.00343cos²a)

Lodlinjens avvikelse från riktningen mot jordens medelpunkt d kan beräknas genom att vi tillämpar sinusteoremet på triangeln:

sind/a_r = sina/a

sind = a_rsina/a =
Rw²cosasina/a =
Rw²sin2a/2a

Från detta uttryck kan vi se att avvikelsen är maximal för a=45^o och noll för a=0^o och a=90^o.

Eftersom a är approximativt lika med a_g och eftersom vinkeln är liten (sind = d) får vi

d = Rw²sin2a/2a_g =
0.0337sin2a/(29.822) =
0.00172sin2a

d i grader blir

d = 1800.00172sin2a/p =
0.0985sin2a grader

Från detta kan vi se att lodlinjens maximala avvikelse (vid latituden 45^o) är c:a 0.1^o.

/Peter E 2006-11-04

Svar:
Hur mycket du väger beror på tyngdaccelerationen g (tyngdkraften blir mg där m är din massa). Tyngdaccelerationen ges enligt fråga [15114] av

g = (M G)/R²

där G är Newtons universella gravitationskonstant, M är planetens massa och R är dess radie. Tyngdaccelerationen ökar alltså med ökande massa M och minskar med ökande radie R. Massor och radier för planeter kan du hitta i Planetary Fact Sheets.

Låt oss räkna ut g på "ytan" av Jupiter:

Jupiters massa M: 189810²⁴ kg

Jupiters radie R: 7010⁶ m

Gravitationskonstanten G: 6.6710^-11 m³/ (kg s²)

g(Jupiter) = (M G)/R² = 26 m/s²

alltså c:a 2.5 gånger jordens.

Se länk 1 för tyngaccelerationen hos fler objekt.

Vi kan skriva om ovanstående uttryck som

g = RGM/R³.

Eftersom medeldensiteten r är proportionell mot M/R³ blir g proportionellt mot

RGr

Större radie ger alltså större g för konstant medeldensitet.

Sedan är det en annan sak att allt detta är ganska teoretiskt för en gas-planet. Eftersom det inte finns någon fast yta har du inget att stå på, så du befinner dig i fritt fall (bortsett från luftmotståndet).
/Peter E 2009-10-07

Svar:
Det finns flera sätt att härleda den erforderliga hastigheten för en satellitbana nära jordytan. Låt oss börja med den mest direkta metoden, se figuren nedan. Om hastigheten för en låg cirkelbana är v så är sträckan mot horisonten på en sekund lika med v1 m. Under en sekund faller föremålet med accelerationen g sträckan

gt²/2 = 9.81/2 m

Jordens radie är r=6.3710⁶ m (Planetary Fact Sheets). I figuren har vi två likformiga trianglar (observera att a är mycket liten så jordens krökning och skillnaden mellan katet och hypotenusa är försumbar):

(9.81/2)/v = (v/2)/r

v² = 9.81r = 9.816.3710⁶ = 62.510⁶

v = 7.9110³ m/s = 7.91 km/s

Man kan även härleda hastigheten från Keplers tredje lag, se fråga [12644]

P² = 4p²a³/(GM)

För en cirkelbana är halva storaxeln a lika med radien r. Om man tar G från fråga [12644] och M från Planetary Fact Sheets, får man

P² = 4p²(6.3710⁶)³/(6.67310^-115.9710²⁴) = 25.610⁶

och

P = 5050 s = 84.2 minuter (omloppstid)

Banhastigheten v blir

v = s/t = 2pr/5050 = 7.9210³ m/s = 7.92 km/s

i god överensstämmelse med värdet ovan.

Länk 1 har en lättillgänglig och trevlig animering av problemet. Länk 2 förklarar relativt ingående. Se även OrbitUnderstanding_orbits och fråga [463].

Se fråga [19564] för en alternativ lösning.

/Peter E 2011-11-30

Svar:
Först måste du räkna ut tyngdaccelerationen på månen. Enligt
fråga [16455] ges månens tyngdacceleration av

g_månen = (M G)/R²

Månens massa M och radie R finns på länk 1. Gravitationskonstanten G är 6.67384×10^-11 m³ kg^-1 s^-2.

g_månen = (0.0734210²⁴ 6.6738410^-11)/(1737.110³)² =
1.62 m/s²

Förhållandet

g_jorden/g_månen = 9.81/1.62 = 6.06

Eriks tyngd på jorden

6.06100 = 606 N

och hans vikt (massa, se fråga [16048]) är

606/9.81 = 61.8 kg

oberoende var han befinner sig.
/Peter E 2014-11-21

Svar:
Alisya!

Såvitt jag förstår är du ute efter att bestämma tyngdaccelerationen g genom att mäta svängningstiden för en plan pendel.

Tyngdacceleration är inom klassisk mekanik den acceleration som är resultatet av kombinationen av gravitationsaccelerationen och den centrifugalacceleration som härrör från en kropps rotation, till exempel jordens rotation. Tyngdaccelerationen på jordytan, också kallad jordaccelerationen, varierar med latitud, mellan cirka 9,78 m/s² vid ekvatorn och 9,83 m/s² vid polerna.
(Tyngdacceleration)

Den formel du ger är korrekt men för en fysikalisk pendel. Problemet med denna är att uttrycket för perioden innehåller flera parametrar som är svåra att uppskatta, speciellt tröghetsmomentet I. Se PendelFysikalisk_pendel.

Man kan i stället använda sig av en enklare modell, en s.k. Matematisk pendel, se PendelMatematisk_pendel. Svängningstiden för en sådan härleds i fråga [14065]:

T = 2p&8730;(l/g)

Som du ser innehåller formeln T, l och g. Genom att mäta l och motsvarande T kan du alltså räkna ut ett värde på g.

För att få ett tillförlitligt svar bör du mäta tiden för flera pendelcykler (l), t.ex. 10-20 stycken. Du kan även göra mätningen med flera pendellängder (l) och ta medelvärdet på resultaten.

Se även fråga [4287].
/Peter E 2021-05-04