Svar:
En geostationär satellit är en satellit som rör sig i en cirkulär omloppsbana i jordens ekvatorialplan, på ett sådant avstånd att en satellit i denna bana roterar runt jorden i samma riktning och med samma omloppstid som jordens rotationstid. Se Geostationary_orbit och bilden nedan. Kommunikationssatelliter och vädersatelliter är normalt geostationära.

Centripetalkraften för en cirkelbana med radien r är mv²/r och
gravitationskrafen är mMG/r², där G är gravitationskonstanten.
Om vi sätter dessa lika får vi

(vinkelhastigheten)² = w² = v²/r² = GM/r³ (1)

Men vinkelhastigheten ges av

w = 2p/P

där P är perioden (omloppstiden).

Jordens rotation bestämmer den nödvändiga vinkelhastigheten, vilket i sin tur bestämmer r. Höjden över jordytan blir då r-R, där R är jordradien.

Vi får eftersom jordens rotationstid i förhållande till stjärnorna är 23 timmar 56 minuter och 4 sekunder:

r³ = GMP²/(4p²) =
6.67310^-115.97410²⁴(236060+5660+4)²/(4p²)

Vilket ger

r = 4.216610⁷ m = 42166 km

Jordens radie är 6378 km så avståndet över jordytan blir

r - R = 42166 - 6378 = 35800 km, dvs c:a en tiondel av avståndet till månen.

Observera att sambandet vinkelhastighet - radie (ekvation 1) är ett sätt att skriva Keplers tredje lag:

(vinkelhastigheten)² = GM/r³ =
(2p/P)² (2)

dvs

GM/(4p ²) = r ³/P ²

där allt i vänsterledet är konstanter.

Anmärkning 1. Vi har i härledningen ovan försummat den stora kroppens acceleration eftersom m är mycket mindre än M. Tar vi hänsyn till denna behöver vi byta ut M i ekvation 2 mot m+M.

Anmärkning 2. Man kan (med lite större besvär) härleda Kelers tredje lag för en elliptisk bana. Uttrycket blir som i ekvation 2 men med radien r utbytt mot halva storaxeln a.

/Peter Ekström 1997-03-20

Svar:
Låt oss först skissa bakgrunden. Från Tycho Brahes mycket exakta mätningar av planeten Mars' rörelse kunde Johannes Kepler få fram tre lagar för planeternas rörelser. Isaac Newton kunde senare förklara dessa rörelser med hjälp av en lag, gravitationslagen, och nyutvecklad matematik (differentialkalkyl).

Keplers första lag: Planetbanorna är ellipser med solen i den ena brännpunkten. (Se nedanstående figur.)

Keplers andra lag: Varje planet rör sig längs sin elliptiska bana med en sådan hastighet att en linje från planeten till solen ("radius vector") alltid sveper över en lika stor area på samma tid. (Se nedanstående figur.) Planeten rör sig alltså snabbare när den är nära solen än när den är längre ifrån.

Från sin gravitationslag kunde Newton härleda följande variant av Keplers tredje lag:



P är (sideriska) omloppstiden

a är halva storaxeln av banan

G är gravitationskonstanten

m₁ och m₂ är objektens massor

Gravitationskonstanten (Gravitational_constant) bestämdes först av Henry Cavendish år 1798 med hjälp av tunga metallkulor och en torsionsvåg. Det aktuella värdet är

G = 6.673 10^-11 m³s^-2kg^-1

Eftersom gravitationskonstanten är svår att mäta är den en av de sämst kända naturkonstanterna.

Om vi sätter in värdet på G och förenklar lite får vi

(m₁+m₂) =
(4p²/G) a³/P² =
5.916 10¹¹ a³/P²

Detta uttryck kan tillämpas på vilket system av två objekt som helst, till exempel Mars och Mars' månar Phobos och Deimos eller t.o.m på ett svart hål i vintergatans centrum (se fråga 6228). Låt oss först tillämpa det på systemet jorden-månen:

(m₁+m₂) = 5.916 10¹¹ (384400000)³/(27.32246060)² = 6.03 10²⁴ kg.

Observera att vi måste använda SI enheter genomgående, dvs meter och sekunder. Från läget av jorden-månens gemensamma tyngdpunkt kan man bestämma m₁/m₂ till 81.3, så jordens massa blir 5.96 10²⁴ kg.

Tillämpat på systemet jorden-solen får vi

(m₁+m₂) = 5.916 10¹¹ (149600000000)³/(365.24246060)² = 1.99 10³⁰ kg.

Eftersom jordens massa kan försummas blir detta solens massa.

För planeter som saknar månar får man mäta deras påverkan av andra planeter. På senare tid har man ju skickat rymdsonder till många planeter, och då kan man bestämma planetens massa från sondens acceleration i närheten av planeten.

Observera att vi även kan bestämma jordens massa med hjälp av tyngdaccererationen 9.81 m/s² och Newtons gravitationslag:

F = ma = (mM G)/r² dvs

M = a r²/G = 9.81 (6.38 10⁶)²/(6.673 10^-11) = 5.98 10²⁴ kg.

Det var denna överensstämmelse som övertygade Newton (och andra) att det var samma kraft som påverkar varje massa på jorden (äpplet :-)) som den kraft som styr solsystemet.

Se även: Kepler's_laws_of_planetary_motion (avancerad), Johannes Kepler: The Laws of Planetary Motion (lite lättare) och Newton's Law of Gravity.

Formelsamling i fysik är en lättillgänglig sammanställning av fysikaliska formler och konstanter. Fysikalisk_konstant och den engelska versionen Physical_constant ger värden på fysikaliska konstanter.

/Peter E 2004-01-24

Svar:
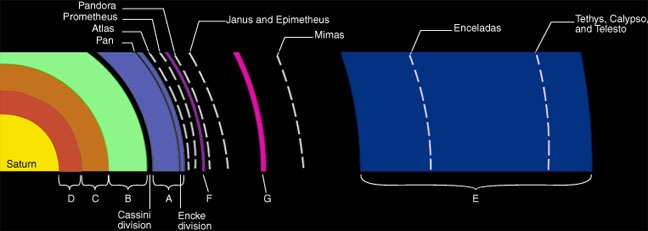
Du har rätt i att ringarnas utseende har att göra med påverkan från de månar som ligger längst in. Det finns, förutom den innersta stora månen Mimas, ett stort antal små månar nära ringarna. I själva verket är ringarna mycket komplexa, se bilden i fråga [3747] och bilden nedan.

Ringarna består av en massa små partiklar - eventuellt resterna efter en måne som brutits sönder. Cassinis delning orsakas av Mimas. Mimas och Cassinis delning har omloppstidsförhållandet 2:1. Det betyder att en partikel i Cassinis delning påverkas av en periodisk kraft i samma riktning, så att delningen så småningom töms på partiklar.

Låt oss visa att omloppsförhållandet Mimas:Cassinis delning är 2:1. För detta behöver vi använda Keplers tredje lag, se fråga [12644]. Om halva storaxeln av banan är a och omloppstiden P, så är a³/P² = konstant. Mimas´ banas halva storaxel är 185520 km (alla sifferuppgifter är från Planetary Fact Sheets). Om Mimas period är 2T, kan vi vänta oss ett gap där omloppstiden är T. Vi får, om vi kallar halva storaxeln där omloppstiden är T för b:

a³/(2T)² = b³/T²

dvs

b³ = a³(T²/(2T)²) =
185520³/4 = 160010¹²

så halvaxeln för delningen blir

b = (160010¹²)^1/3 = 117000 km

vilket stämmer bra med värdet 117580-122170 från Planetary Fact Sheets.

Se även länken Saturnus' ringar nedan.

/Peter E 2005-05-13

Svar:
Det är kanske inte helt lätt att förstå, men överföringen av massa från en mindre komponent får faktiskt neutronstjärnan (=pulsaren) att rotera snabbare, se länk 1 och den rudimentära Wikipedia-artikeln i Neutron_star_spin-up.

Material från stjärnan kommer att samlas i en skiva som innan den kommer i kontakt med pulsaren roterar enligt Keplers lagar - ungefär som Saturnus´ ringar. Se nedanstående figur hur det kan tänkas se ut.

Vi tillämpar Keplers tredje lag



på en partikel som rör sig 20 km från neutronstjärnans centrum. Neutronstjärnan är mindre än detta, så partikeln rör sig fritt i en keplerbana. Om vi mäter massan i solmassor, omloppstiden P i år och avståndet a i astronomiska enheter (AE) får vi:

(P²/a³)(m₁+m₂) = 1

Om partikeln har en liten massa och neutronstjärnan en massa av 3 solmassor får vi:

P² = a³/3

Avståndet a i AE blir

a = 20/150,000,000 = 1.3310^-7

Omloppstiden blir

P = sqrt((1.3310^(-7))^3/3)365.242460601000 = 0.88 millisekunder

Även en nybildad pulsar spinner långsammare än detta, så när partikeln får kontakt med pulsaren (genom magnetfältet eller kontakt med ytan), så kommer den att få pulsaren att rotera snabbare.

/Peter E 2007-05-10

Svar:
Årstider är inte väldefinierat eftersom de definieras av temperaturer och därmed varierande väder. För din fråga är det bättre att tala om sommar- och vinterhalvår. Dessa definieras som skillnaden mellan vår- och höstdagjämningar, det vill säga de tidpunkter när solen passerar himmelsekvatorn.

I artikeln Equinox finns en tabell med tidpunkter för vår- och höstdagjämningar.

Sommarhalvåret 2011 är från 20/3 kl. 23:21 till 23/9 kl. 09:04 dvs 186 dagar och 10 timmar.

Vinterhalvåret 2011-12 är från 23/9 kl. 09:04 till 20/3 kl. 05:14 dvs 178 dagar och 20 timmar.

(Länk 1 innehåller en kalkylator för tidsintervall.)

Låt oss först kontrollera att intervallen är korrekta:
178d 20t + 186d 10t = 364d 30t = 365d 6t = 365.25

vilket stämmer bra med årets längd (en skottdag vart fjärde år).

Efter att ha etablerat sommar- och vinterhalvårets längd, tillbaka till frågan. Sommarhalvåret är alltså ungefär 7 dygn längre än vinterhalvåret.

Det beror på att jorden är närmast solen den 3 januari (nära vintersolståndet den 21 december) och längst ifrån den 4 juli (EarthAxial_tilt_and_seasons).

Jorden rör sig alltså lite snabbare i sin bana i januari än i juli. Medelhastigheten över halvåret blir då större under vinterhalvåret, varför detta blir kortare.

Den bakomliggande orsaken är Keplers andra lag (se fråga [12644]) som innebär att en planet rör sig snabbare när den är nära solen än när den är längre ifrån. Med ett modernt synsätt beror detta på att den potentiella energin är lägre när avståndet är litet varför rörelseenergin blir större.

Om jorden är närmast solen i januari, borde vi då inte få mildare vintrar och svalare somrar på norra halvklotet än på södra? Eftersom halvkloten är så olika (södra är nästan uteslutande hav, norra har flera stora kontinenter) är det inte meningsfullt att jämföra somrar/vintrar på de två halvkloten.

I fråga [830] diskuteras orsaken till istiderna. Det är alltså till en del den varierande excenticiteten (avlångheten) hos jordens bana som orsakar istiderna.

/fa2012_1
/Peter E 2011-09-07

Svar:
Det finns flera sätt att härleda den erforderliga hastigheten för en satellitbana nära jordytan. Låt oss börja med den mest direkta metoden, se figuren nedan. Om hastigheten för en låg cirkelbana är v så är sträckan mot horisonten på en sekund lika med v1 m. Under en sekund faller föremålet med accelerationen g sträckan

gt²/2 = 9.81/2 m

Jordens radie är r=6.3710⁶ m (Planetary Fact Sheets). I figuren har vi två likformiga trianglar (observera att a är mycket liten så jordens krökning och skillnaden mellan katet och hypotenusa är försumbar):

(9.81/2)/v = (v/2)/r

v² = 9.81r = 9.816.3710⁶ = 62.510⁶

v = 7.9110³ m/s = 7.91 km/s

Man kan även härleda hastigheten från Keplers tredje lag, se fråga [12644]

P² = 4p²a³/(GM)

För en cirkelbana är halva storaxeln a lika med radien r. Om man tar G från fråga [12644] och M från Planetary Fact Sheets, får man

P² = 4p²(6.3710⁶)³/(6.67310^-115.9710²⁴) = 25.610⁶

och

P = 5050 s = 84.2 minuter (omloppstid)

Banhastigheten v blir

v = s/t = 2pr/5050 = 7.9210³ m/s = 7.92 km/s

i god överensstämmelse med värdet ovan.

Länk 1 har en lättillgänglig och trevlig animering av problemet. Länk 2 förklarar relativt ingående. Se även OrbitUnderstanding_orbits och fråga [463].

Se fråga [19564] för en alternativ lösning.

/Peter E 2011-11-30

Svar:
Man "väger" en stjärna genom att följa rörelsen hos ett objekt (normalt en annan stjärna i ett dubbelstjärnesystem) och tillämpa den moderna varianten av Keplers tredje lag, se fråga [12644].

Genom att studera spektra från sjärnor kan man lära sig hur olika stjärnor ser ut. Då kan man bestämma massor från avståndet och ljusstyrkan med hjälp av mass-luminositetsrelationen, se mass-luminositetsrelation.

Se fråga [6228] för en beskrivning hur man på samma sätt väger ett svart hål.

Som ofta i vetenskapen sker framstegen i små steg som bygger på tidigare kunskap. I fallet stjärnors massa kan man se en tydlig progression:

Tycho-Brahe (Tycho_Brahe) gjorde i slutet av 1500-talet exakta mätningar av planeten Mars rörelse.

Dessa data användes av Johannes Kepler (Johannes_Kepler) för att komma fram till tre lagar (början av 1600-talet, fråga [12644]).

Isaac Newton (Isaac_Newton) generaliserade Keplers tredje lag i termer av en generell gravitationslag (slutet av 1600-talet, fråga [12834]).

Henry Cavendish (Henry_Cavendish) bestämde ett värde på gravitationskonstanten G i Newtons gravitationslag (slutet av 1700-talet).

Sedan dröjde det till slutet av 1800-talet innan man hade tillräckligt bra teleskop och spektrografer för att kunna bestämma stjärnmassor. Det tog alltså nära 300 år att komma fram till hur man kunde bestämma massan hos stjärnor och andra astronomiska objekt.
/Peter E 2012-12-12

Svar:
Hej Anton! Eftersom du refererar till hastigheter nära ljushastigheten så duger inte de uttryck du använder. Du måste använda uttryck enligt den speciella relativitetsteorin. Detta diskuteras i Schwarzschild_radiusRelativistic_circular_orbits_and_the_photon_sphere.

Från Keplers lag (fråga [12644]) får man för en cirkulär bana, som du mycket riktigt säger,

r = GM/v²

Detta gäller emellertid bara för icke-relativistiska värden på v. Det relativistiska uttrycket ger

(v/c)² (r/r_S - 1) = 1/2

För v = c blir detta

r = 3r_S/2

där

r_S = 2GM/c² (se fråga [18930])

Detta betyder att banan i själva verket ligger utanför Schwarzschildradien r_S. Denna bana kallas foton-sfären eftersom fotoner med hastigheten c kan röra sig i en stabil cirkelbana.

Se även länk 1 (figuren nedan) och Photon_sphere.

/Peter E 2017-05-22