Vill du ha ett snabbt svar - sök i databasen
Nyckelord: kraft
40 träffar
Vad gör man med det radioaktiva avfallet från kärnkraftverken?
Fråga:
Jag undrar vad man gör med det radioaktiva avfallet från kärnkraftverken?
I vad lagras strålningen för att den inte ska komma ut i naturen?
/Magda K, Alfaskolan, Solna 2006-03-10
Jag undrar vad man gör med det radioaktiva avfallet från kärnkraftverken?
I vad lagras strålningen för att den inte ska komma ut i naturen?
/Magda K, Alfaskolan, Solna 2006-03-10
Svar:
Hej Magda! Vi har svarat en hel del på frågor om vad avfallet består av, sekärnkraftsavfall , men inte mycket vad vi planerar gör med det. Så är beskrivs processen av Svensk Kärnbränslehantering AB (SKB):
(SKB):
Man har alltså tre barriärer för att hindra att radioaktivitet kommer ut: kopparkapsel, lera och urberget.
Den mest sannolika placeringen tycks i dag vara i Oskarshamns-trakten (där mellanlagringen Clab finns i dag), men detaljerna i förvaret kan fortfarande ändras - det är inte byggstart förrän 2010 och förvaret beräknas komma i drift 2017.
För mer information om avfall och slutförvaring se Svensk Kärnbränslehantering AB s webbsajt och den mycket informativa sajten för ungdomar under länk 1 med bland annat några bra kortfilmer.
s webbsajt och den mycket informativa sajten för ungdomar under länk 1 med bland annat några bra kortfilmer.
Hej Magda! Vi har svarat en hel del på frågor om vad avfallet består av, se
Idag mellanlagras allt använt kärnbränsle i Clab där vatten kyler bränslet och skärmar av strålningen. Eftersom använt kärnbränsle har en förhöjd aktivitet under väldigt lång tid, storleksordningen 100 000 år, måste förvaringen förändras i framtiden.
Därför planerar SKB att bygga ett slutförvar för allt använt kärnbränsle, ett förvar som inte kräver någon övervakning och kontroll av kommande generationer.
Den metod som SKB arbetar efter kallas KBS-3. Den innebär att det använda kärnbränslet ska kapslas in i koppar. Kopparkapslarna ska sedan deponeras i urberget på cirka 500 meters djup, inbäddade i lera (se illustrationen nedan). När deponeringen är klar försluts tunnlar och bergrum.
Man har alltså tre barriärer för att hindra att radioaktivitet kommer ut: kopparkapsel, lera och urberget.
Den mest sannolika placeringen tycks i dag vara i Oskarshamns-trakten (där mellanlagringen Clab finns i dag), men detaljerna i förvaret kan fortfarande ändras - det är inte byggstart förrän 2010 och förvaret beräknas komma i drift 2017.
För mer information om avfall och slutförvaring se Svensk Kärnbränslehantering AB

Hur skall man dosera vägen i en kurva?
Fråga:
Håller på med centralrörelse och tyckte då att det skulle vara kul att räkna lite på vilka farter som är möjliga i en doserad kurva utan att bilen får sladd. Gjorde en hel del förenklingar. Införde följande krafter tyngdkraften och normalkraften och en friktionskraft mellan vägbanan och däcken. Friktionskraften bör väll vara riktad innåt i kurvan men längs vägbanan? Friktionskraften får då en vertikal komposant som är riktad neråt och alltså samverkar med tyngdkraften, vilket känns lite märkligt. Kan det vara så? Hur löser man den här typen av problem?
/Marianne A, Ehrensvärdska, Karlskrona 2006-09-19
Håller på med centralrörelse och tyckte då att det skulle vara kul att räkna lite på vilka farter som är möjliga i en doserad kurva utan att bilen får sladd. Gjorde en hel del förenklingar. Införde följande krafter tyngdkraften och normalkraften och en friktionskraft mellan vägbanan och däcken. Friktionskraften bör väll vara riktad innåt i kurvan men längs vägbanan? Friktionskraften får då en vertikal komposant som är riktad neråt och alltså samverkar med tyngdkraften, vilket känns lite märkligt. Kan det vara så? Hur löser man den här typen av problem?
/Marianne A, Ehrensvärdska, Karlskrona 2006-09-19
Svar:
Marianne! Att räkna med friktion är ganska besvärligt eftersom det är svårt att veta vad friktionskoefficienten är. Det väsentliga i ditt problem är väl ändå doseringen, dvs vägens lutning i en kurva. Låt oss först definiera några storheter.
bilens massa = m
tyngdaccelerationen = g
normalkraften = N
doseringsvinkel = a
bilens hastighet = v
kurvradie = r
Bilen påverkas av två krafter: normalkraften N från vägbanan och mg från tyngdkraften. Om vi sätter samman dessa får vi en resulterande horisontell kraft R mot vägens krökningscentrum. Det är denna kraft som ger den acceleration som får bilen att röra sig med en cirkelbana. Accelerationen är
mv2/r = R = mgtana
Vi får alltså sambandet
v2 = rgtana
För en viss given hastighet och kurvradie kan vi alltså med detta uttryck beräkna den optimala doseringsvinkeln. Bilen kan naturligtvis även ta kurvan med en annan hastighet, men då behöver vifriktion för att hålla den kvar på vägen. Om hastigheten är större än v får du mycket riktigt en vertikal komposant. Detta gör att normalkraften ökar, dvs bilen "trycks" mot vägbanan.
Vi har, eftersom vi betraktar bilen från vägens perspektiv, inte infört någoncentrifugalkraft , utan vi har en resulterande kraft R som ger en centripetalacceleration.
Marianne! Att räkna med friktion är ganska besvärligt eftersom det är svårt att veta vad friktionskoefficienten är. Det väsentliga i ditt problem är väl ändå doseringen, dvs vägens lutning i en kurva. Låt oss först definiera några storheter.
bilens massa = m
tyngdaccelerationen = g
normalkraften = N
doseringsvinkel = a
bilens hastighet = v
kurvradie = r
Bilen påverkas av två krafter: normalkraften N från vägbanan och mg från tyngdkraften. Om vi sätter samman dessa får vi en resulterande horisontell kraft R mot vägens krökningscentrum. Det är denna kraft som ger den acceleration som får bilen att röra sig med en cirkelbana. Accelerationen är
mv2/r = R = mgtana
Vi får alltså sambandet
v2 = rgtana
För en viss given hastighet och kurvradie kan vi alltså med detta uttryck beräkna den optimala doseringsvinkeln. Bilen kan naturligtvis även ta kurvan med en annan hastighet, men då behöver vi
Vi har, eftersom vi betraktar bilen från vägens perspektiv, inte infört någon

Hur mycket påverkas lodlinjens rikning av den centrifugalkraft som jordrotationen ger upphov till?
Fråga:
Om man står på marken bör man se till att hålla sin egen tyngdpunkt på en linje genom jordens tyngdpunkt och sina egna fötter, annars trillar man ikull. Men, hur muycket påverkar den centrifugalkraft som jordrotationen ger upphov till detta? Inte alls om man står på ekvatorn eller nord(syd)polen. Men i Skåne! Hur många grader (eller fraktioner av en grad) måste man luta sig "inåt" (dvs mot norr) för att inte falla ikull pga centrifugalkraften?
/Jon L, 2006-11-03
Om man står på marken bör man se till att hålla sin egen tyngdpunkt på en linje genom jordens tyngdpunkt och sina egna fötter, annars trillar man ikull. Men, hur muycket påverkar den centrifugalkraft som jordrotationen ger upphov till detta? Inte alls om man står på ekvatorn eller nord(syd)polen. Men i Skåne! Hur många grader (eller fraktioner av en grad) måste man luta sig "inåt" (dvs mot norr) för att inte falla ikull pga centrifugalkraften?
/Jon L, 2006-11-03
Svar:
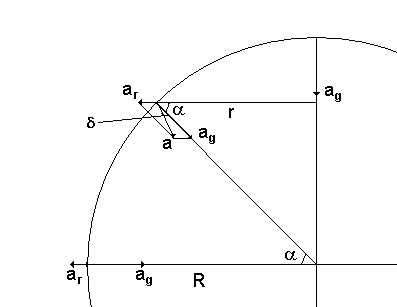
Jon! Det är en helt omärkbar effekt och det är knappast någon risk att man trillar, men låt oss som en övning räkna ut hur stor effekten är. Vi antar att jorden är klotformad och homogen med radien R. Den enda effekt vi tar hänsyn till är jordens rotation, vi bortser alltså från tillplattningen. Vi inför några beteckningar (se figuren):
ag = 9.822 m/s2 tyngdaccelerationen från jordens dragningskraft, se länk 1
ar accelerationen pga jordens rotation
a den resulterande tyngdaccelerationen
R = 6.37106 m jordradien
a latituden
w = 2p/(246060) = 72.710-6 s-1 vinkelhastigheten för jordens rotation
Vid polerna och ekvatorn är det ingen avvikelse i vinkel mellan a och ag (precis som du säger) medan det för medelhöga latituder är en avvikelse så att det är en liten "uppförsbacke" när man går norrut. Om du så vill kan du förstå detta som att "centrifugalkraften" försöker hindra dig att gå närmare rotationsaxeln.
Låt oss börja med att se vad som händer vid ekvatorn. Rotationshastigheten ges av
v = Rw = 6.3710672.710-6 = 463 m/s
Accelerationen pga rotationen blir
ar = v2/R = Rw2 = 6.37106(72.710-6)2 = 0.0337 m/s2
Tyngdaccelerationen vid ekvatorn blir alltså
ag - ar = 9.822 - 0.0337 = 9.788 m/s2
Accelerationen pga rotationen vid latituden a blir
ag = rw2 = Rcosaw2
Tillämpning av cosinuseoremet på triangeln ag, ar, a ger
a2 = ag2 + ar2 -2agarcos(a)
Den andra termen i högra ledet är mycket liten så vi kan försumma den. Vi får då
a = ag(1 - 2Rw2cos2a/ag)1/2 = ag(1 - Rw2cos2a/ag) =
ag(1 - 0.0337cos2a/9.822)
a = ag(1 - 0.00343cos2a)
Lodlinjens avvikelse från riktningen mot jordens medelpunkt d kan beräknas genom att vi tillämpar sinusteoremet på triangeln:
sind/ar = sina/a
sind = arsina/a =
Rw2cosasina/a =
Rw2sin2a/2a
Från detta uttryck kan vi se att avvikelsen är maximal för a=45o och noll för a=0o och a=90o.
Eftersom a är approximativt lika med ag och eftersom vinkeln är liten (sind = d) får vi
d = Rw2sin2a/2ag =
0.0337sin2a/(29.822) =
0.00172sin2a
d i grader blir
d = 1800.00172sin2a/p =
0.0985sin2a grader
Från detta kan vi se att lodlinjens maximala avvikelse (vid latituden 45o) är c:a 0.1o.
Jon! Det är en helt omärkbar effekt och det är knappast någon risk att man trillar, men låt oss som en övning räkna ut hur stor effekten är. Vi antar att jorden är klotformad och homogen med radien R. Den enda effekt vi tar hänsyn till är jordens rotation, vi bortser alltså från tillplattningen. Vi inför några beteckningar (se figuren):
ag = 9.822 m/s2 tyngdaccelerationen från jordens dragningskraft, se länk 1
ar accelerationen pga jordens rotation
a den resulterande tyngdaccelerationen
R = 6.37106 m jordradien
a latituden
w = 2p/(246060) = 72.710-6 s-1 vinkelhastigheten för jordens rotation
Vid polerna och ekvatorn är det ingen avvikelse i vinkel mellan a och ag (precis som du säger) medan det för medelhöga latituder är en avvikelse så att det är en liten "uppförsbacke" när man går norrut. Om du så vill kan du förstå detta som att "centrifugalkraften" försöker hindra dig att gå närmare rotationsaxeln.
Låt oss börja med att se vad som händer vid ekvatorn. Rotationshastigheten ges av
v = Rw = 6.3710672.710-6 = 463 m/s
Accelerationen pga rotationen blir
ar = v2/R = Rw2 = 6.37106(72.710-6)2 = 0.0337 m/s2
Tyngdaccelerationen vid ekvatorn blir alltså
ag - ar = 9.822 - 0.0337 = 9.788 m/s2
Accelerationen pga rotationen vid latituden a blir
ag = rw2 = Rcosaw2
Tillämpning av cosinuseoremet på triangeln ag, ar, a ger
a2 = ag2 + ar2 -2agarcos(a)
Den andra termen i högra ledet är mycket liten så vi kan försumma den. Vi får då
a = ag(1 - 2Rw2cos2a/ag)1/2 = ag(1 - Rw2cos2a/ag) =
ag(1 - 0.0337cos2a/9.822)
a = ag(1 - 0.00343cos2a)
Lodlinjens avvikelse från riktningen mot jordens medelpunkt d kan beräknas genom att vi tillämpar sinusteoremet på triangeln:
sind/ar = sina/a
sind = arsina/a =
Rw2cosasina/a =
Rw2sin2a/2a
Från detta uttryck kan vi se att avvikelsen är maximal för a=45o och noll för a=0o och a=90o.
Eftersom a är approximativt lika med ag och eftersom vinkeln är liten (sind = d) får vi
d = Rw2sin2a/2ag =
0.0337sin2a/(29.822) =
0.00172sin2a
d i grader blir
d = 1800.00172sin2a/p =
0.0985sin2a grader
Från detta kan vi se att lodlinjens maximala avvikelse (vid latituden 45o) är c:a 0.1o.
Vad är kraft?
Fråga:
Vad är kraft?
/Olivia G, vasaskolan, skövde 2007-02-04
Vad är kraft?
/Olivia G, vasaskolan, skövde 2007-02-04
Svar:
Olivia! Nationalencyklopedin säger: kraft, intuitivt ett välbekant vardagsbegrepp, men bakom sinnesförnimmelserna en svårfångad abstraktion.
säger: kraft, intuitivt ett välbekant vardagsbegrepp, men bakom sinnesförnimmelserna en svårfångad abstraktion.
Wikipedias definition är lite mer konkret (se Kraft ): kraftbegreppet är en abstraktion inom fysiken för att förklara och beskriva orsaken till förändringar i ett systems rörelse.
): kraftbegreppet är en abstraktion inom fysiken för att förklara och beskriva orsaken till förändringar i ett systems rörelse.
Den grundläggande definitionen är attkraft är alla företeelser som ändrar en kropps rörelsemängd p = m·v:
F = dp/dt = d(mv)/dt = m·dv/dt = m·a
Det finns många olika sorters krafter. De fundamentala kraftverkningarna är gravitationskraft, den svaga kraften, elektromagnetisk kraft och färgkraften.
Sedan finns andra yttringar av kraft, t.ex. rekylkraft, friktionskraft och elastisk kraft. Se vidareForce .
/Peter E 2007-02-05
Olivia! Nationalencyklopedin
Wikipedias definition är lite mer konkret (se Kraft
 ): kraftbegreppet är en abstraktion inom fysiken för att förklara och beskriva orsaken till förändringar i ett systems rörelse.
): kraftbegreppet är en abstraktion inom fysiken för att förklara och beskriva orsaken till förändringar i ett systems rörelse.Den grundläggande definitionen är att
F = dp/dt = d(mv)/dt = m·dv/dt = m·a
Det finns många olika sorters krafter. De fundamentala kraftverkningarna är gravitationskraft, den svaga kraften, elektromagnetisk kraft och färgkraften.
Sedan finns andra yttringar av kraft, t.ex. rekylkraft, friktionskraft och elastisk kraft. Se vidare
/Peter E 2007-02-05
Om gluoner
Fråga:
svårt hålla isär:
mesoner växelverkar alltså mellan protoner/neutroner, medan gluoner växelverkar mellan kvarkar. Om det finns 8 olika gluoner, så hur skiljer man dem, vad har de för beteckning, tecken? Mvh
/alf e, ascheberg, gbg 2007-02-19
svårt hålla isär:
mesoner växelverkar alltså mellan protoner/neutroner, medan gluoner växelverkar mellan kvarkar. Om det finns 8 olika gluoner, så hur skiljer man dem, vad har de för beteckning, tecken? Mvh
/alf e, ascheberg, gbg 2007-02-19
Svar:
Alf! Det finns 8 olika gluoner. Alla med färg/antifärg kombinationer. Eftersom det finns tre färger - rött, grönt, blått - tycker man att det skulle finnas 9 gluoner. Av subtila skäl som är ganska svårt att förstå finns det i själva verket bara 8 gluoner, seGluon och länk 1.
Den speciella kombinationen som faller bort är
Anledningen är att denna skulle kunna växelverka med vilken färg som helst utan att ändra egenskaper. Någon sådan växelverkan har inte observerats, så denna kombination faller bort.
Lite förenklat fungerar utbytet av gluoner som i nedanstående tabell. Vi utgår från en röd och en grön kvark (1). Den gröna kvarken sänder ut en grön/antiröd gluon och blir röd (2). Den ursprungliga röda kvarken absorberar gluonen och blir grön (3). Kvarkarna har alltså bytt färger och det är detta som ger attraktionen.
/Peter E 2007-02-19
Alf! Det finns 8 olika gluoner. Alla med färg/antifärg kombinationer. Eftersom det finns tre färger - rött, grönt, blått - tycker man att det skulle finnas 9 gluoner. Av subtila skäl som är ganska svårt att förstå finns det i själva verket bara 8 gluoner, se
Den speciella kombinationen som faller bort är
(röd-antiröd + grön-antigrön + blå-antiblå)/sqrt(3)
Anledningen är att denna skulle kunna växelverka med vilken färg som helst utan att ändra egenskaper. Någon sådan växelverkan har inte observerats, så denna kombination faller bort.
Lite förenklat fungerar utbytet av gluoner som i nedanstående tabell. Vi utgår från en röd och en grön kvark (1). Den gröna kvarken sänder ut en grön/antiröd gluon och blir röd (2). Den ursprungliga röda kvarken absorberar gluonen och blir grön (3). Kvarkarna har alltså bytt färger och det är detta som ger attraktionen.
1 R G
.
2 R granti R
.
3 G R
/Peter E 2007-02-19
Är det växelspänning eller likspänning i högspänningsledningarna?
Fråga:
Är det växelspänning eller likspänning i högspänningsledningarna? Jag har läst flera olika källor och de motsäger varandra. Är det någon ny teknik som gör att det blir en mindre förlust om man överför spännningen likriktad?
/Annika K, Nyströmska skolan, Söderköping 2007-11-13
Är det växelspänning eller likspänning i högspänningsledningarna? Jag har läst flera olika källor och de motsäger varandra. Är det någon ny teknik som gör att det blir en mindre förlust om man överför spännningen likriktad?
/Annika K, Nyströmska skolan, Söderköping 2007-11-13
Svar:
De stora ledningarna (från kärnkraftverken och Norrland) är 380 kV växelström. EnligtElectric_power_transmission är ledningarna normalt en aluminium-legering tillverkad av flera trådar och förstärkta med ståltrådar (se bild i länk 1). Koppar användes ibland, men aluminium har lägre vikt för given kapacitet och är dessutom mycket billigare.
Ledningar i havet är ofta högspänd likström - med eller utan returledning. Man kan använda vattnet för att sluta slingan men då får man en oönskad ström genom vattnet/marken. Högspänd likström (HVDC ) utvecklades tidigt av ASEA och de (ABB numera) är forfarande en ledande tillverkare.
Anledningen till att man vill ha hög spänning är att resistansförlusterna blir mindre med ökande spänning. Den transporterade effekten är
P = UI dvs I = P/U
Resistansförlusterna om ledningens resistans är r blir
Pr = rI2 = r(P/U)2
För givet P och r minskar alltså resistansförlusterna med ökande U.
Växelspänning ger även vissa kapacitetsförluster - speciellt i vatten som ökar dessa förluster. Anledningen till att man inte enbart använder högspänd likström är att transformeringen växelspänning-likspänning-växelspänning är komplicerad och ger förluster. Speciellt bökigt blir det om man vill ta ut den del ström längs ledningen. Detta är enkelt med transformatorer om man använder växelspänning, men inte effektivt med likström. Behovet av avtappning vid transport under vatten finns ju knappast.
SeBaltic_Cable för information om kabeln mellan Sverige och Tyskland som faktiskt enligt artikeln saknar returledning! Förutom att vi alltså skickar ström genom de stackars torskarna i Östersjön så får vi i Sverige betala tyska höga priser för elenergin i stället för det traditionellt låga svenska priserna! Man har emellertid lagt ner dubbla ledare eftersom man i samband med bygget fick kritik från miljörörelsen. Men i stället för att använda den andra ledningen som returledning kör man nu båda parallellt och alltså utan returledning!
Jag stiger nu ner igen från min apelsinlåda :-).
Fotnot om system utan returledning:
System med högspänd likström utan returledning (SWER) beskrivs i en Wikipedia-artikelSingle_wire_earth_return . Där säger man bland annat:
Systemen sägs alltså vara oskadliga, men det råder det inte enighet om.
/Peter E 2007-11-13
De stora ledningarna (från kärnkraftverken och Norrland) är 380 kV växelström. Enligt
Ledningar i havet är ofta högspänd likström - med eller utan returledning. Man kan använda vattnet för att sluta slingan men då får man en oönskad ström genom vattnet/marken. Högspänd likström (
Anledningen till att man vill ha hög spänning är att resistansförlusterna blir mindre med ökande spänning. Den transporterade effekten är
P = UI dvs I = P/U
Resistansförlusterna om ledningens resistans är r blir
Pr = rI2 = r(P/U)2
För givet P och r minskar alltså resistansförlusterna med ökande U.
Växelspänning ger även vissa kapacitetsförluster - speciellt i vatten som ökar dessa förluster. Anledningen till att man inte enbart använder högspänd likström är att transformeringen växelspänning-likspänning-växelspänning är komplicerad och ger förluster. Speciellt bökigt blir det om man vill ta ut den del ström längs ledningen. Detta är enkelt med transformatorer om man använder växelspänning, men inte effektivt med likström. Behovet av avtappning vid transport under vatten finns ju knappast.
Se
Jag stiger nu ner igen från min apelsinlåda :-).
Fotnot om system utan returledning:
System med högspänd likström utan returledning (SWER) beskrivs i en Wikipedia-artikel
SWER violates common wisdom about electrical safety, because it lacks a traditional metallic return to a neutral shared by the generator. SWER’s safety is instead assured because transformers isolate the ground from both the generator and user.
Systemen sägs alltså vara oskadliga, men det råder det inte enighet om.
/Peter E 2007-11-13
Hur stora g-krafter utsätts en utförsåkare för?
Fråga:
Hej! Vilka krafter utsätts en utförsåkare för (g-kraft)? :)
/Sara B, Nya Läroverket, Luleå 2009-02-17
Hej! Vilka krafter utsätts en utförsåkare för (g-kraft)? :)
/Sara B, Nya Läroverket, Luleå 2009-02-17
Svar:
Sara! Tyngdkraften rakt nedåt, normalkraften vinkelrätt uppåt från backen, friktionkraften bakåt längst skidan och till slut luftmotståndet i en riktning motsatt färdriktningen.
Det var ett svar som frågan är formulerad. Men du menade antagligen vilken g-kraft en skidåkare kan utsättas för när hon svänger. Accelerationen a i en cirkelbana med radien r är
a = F/m = v2/r
där v är hastigheten. Låt oss anta hastigheten för en störtloppsåkare är 100 km/tim och krökningsradien r 50 m. Hastigheten 100 km/tim är 100000/3600 = 28 m/s, så vi får
a = 282/50 = 15.68 m/s2 = (15.68/9.81) g = 1.60 g.
Denna g-kraft är alltså riktad utåt, bort från krökningscentrum. Till denna komponent får man sedan addera tyngskraftkomponenten 1g riktad nedåt. Resultanten av dessa två blir då med hjälp av Pythagoras sats:
sqrt(11+1.61.6)g = 1.90g
Under korta perioder kan man nog tänka sig t.o.m. tvärare svängar än detta, så man kan förstå varför en störtloppsåkare är så trött efter bara ett par minuters åkning.
/Peter E 2009-02-18
Sara! Tyngdkraften rakt nedåt, normalkraften vinkelrätt uppåt från backen, friktionkraften bakåt längst skidan och till slut luftmotståndet i en riktning motsatt färdriktningen.
Det var ett svar som frågan är formulerad. Men du menade antagligen vilken g-kraft en skidåkare kan utsättas för när hon svänger. Accelerationen a i en cirkelbana med radien r är
a = F/m = v2/r
där v är hastigheten. Låt oss anta hastigheten för en störtloppsåkare är 100 km/tim och krökningsradien r 50 m. Hastigheten 100 km/tim är 100000/3600 = 28 m/s, så vi får
a = 282/50 = 15.68 m/s2 = (15.68/9.81) g = 1.60 g.
Denna g-kraft är alltså riktad utåt, bort från krökningscentrum. Till denna komponent får man sedan addera tyngskraftkomponenten 1g riktad nedåt. Resultanten av dessa två blir då med hjälp av Pythagoras sats:
sqrt(11+1.61.6)g = 1.90g
Under korta perioder kan man nog tänka sig t.o.m. tvärare svängar än detta, så man kan förstå varför en störtloppsåkare är så trött efter bara ett par minuters åkning.
/Peter E 2009-02-18
Varför flyger man utåt om man åker fortare i en karusell som ser ut som Kättingflygaren på Gröna Lund?
Fråga:
Varför flyger man utåt om man åker fortare i en karusell som ser ut som Kättingflygaren på Gröna Lund?
/Johanna 2009-03-09
Varför flyger man utåt om man åker fortare i en karusell som ser ut som Kättingflygaren på Gröna Lund?
/Johanna 2009-03-09
Svar:
Johanna! Karusellen ser ut som den på bilden nedan frånChair-O-Planes .
För att sitsarna med (eller utan) passagerare skall röra sig i en cirkelbana erfordras en kraft riktad mot centrum. Denna s.k. centripetalkraft ges av
Fr = mv2/r
Om rotationshastigheten v ökar ökar radien r och vinkeln a mellan vertikalplanet och kättingen minskar för att centripetalkraften skall öka, se figuren nedan.
Det är två krafter som tillsammans orsakar nettokraften Fr (de två steckade krafterna i figuren):
1 Spänningen i upphängningskedjan FF riktad snett uppåt i kedjans riktning.
2 Tyngdkraften FG = mg riktad rakt nedåt.
Från triangeln med FF och Fr får man
tan a = Fr/FG
dvs
Fr = tanaFG = tanamg
Men enligt ovan var ju
Fr = mv2/r
dvs
mv2/r = tanamg
eller
v2 = rtanag
Vi ser för det första att sambandet inte beror av massan m.
Om avståndet från rotationscentrum till upphängningspunken är r0 blir radien
r = r0 + lsina
där l är kedjans längd. Vi får alltså till slut sambandet
v2 = (r0 + lsina)tanag
Vi ser att om hastigheten v ökar så måste även vinkeln a öka. Ekvationen ovan är svår att lösa exakt, men i appleten under länk 2 kan man variera parametrarna och se vad som händer.
Se Slagkraft - Naturvetenskap på Liseberg för mer om Kättingflygaren och andra Liseberg-attraktioner.
för mer om Kättingflygaren och andra Liseberg-attraktioner.
Se även Kättingflygare .
.
Johanna! Karusellen ser ut som den på bilden nedan från
För att sitsarna med (eller utan) passagerare skall röra sig i en cirkelbana erfordras en kraft riktad mot centrum. Denna s.k. centripetalkraft ges av
Fr = mv2/r
Om rotationshastigheten v ökar ökar radien r och vinkeln a mellan vertikalplanet och kättingen minskar för att centripetalkraften skall öka, se figuren nedan.
Det är två krafter som tillsammans orsakar nettokraften Fr (de två steckade krafterna i figuren):
1 Spänningen i upphängningskedjan FF riktad snett uppåt i kedjans riktning.
2 Tyngdkraften FG = mg riktad rakt nedåt.
Från triangeln med FF och Fr får man
tan a = Fr/FG
dvs
Fr = tanaFG = tanamg
Men enligt ovan var ju
Fr = mv2/r
dvs
mv2/r = tanamg
eller
v2 = rtanag
Vi ser för det första att sambandet inte beror av massan m.
Om avståndet från rotationscentrum till upphängningspunken är r0 blir radien
r = r0 + lsina
där l är kedjans längd. Vi får alltså till slut sambandet
v2 = (r0 + lsina)tanag
Vi ser att om hastigheten v ökar så måste även vinkeln a öka. Ekvationen ovan är svår att lösa exakt, men i appleten under länk 2 kan man variera parametrarna och se vad som händer.
Se Slagkraft - Naturvetenskap på Liseberg
Se även Kättingflygare
 .
.
Berg-och-dal bana med loop
Fråga:
Frågan gäller en berg-och-dal bana med en loop.
Hur stor är centripetalaccelerationen längst upp på karusellen? Var är centripetalaccelerationen som störst?
/Ali z, BORGARSKOLAN, MALMÖ 2009-11-05
Frågan gäller en berg-och-dal bana med en loop.
Hur stor är centripetalaccelerationen längst upp på karusellen? Var är centripetalaccelerationen som störst?
/Ali z, BORGARSKOLAN, MALMÖ 2009-11-05
Svar:
Ali! Jag hade lite svårt att förstå din fråga. Det du frågar om är nog en berg-och-dalbana (Roller_coaster , Roller_coaster_elements ) med en loop (Vertical_loop ), se nedanstående foto av den första loopen (Coney Island, New York) från Wikimedia Commons. Jag har kortat ner din fråga något.
Jag tänkte ta upp ett par saker av vad jag tror du frågade om: hur räknar man ut vagnens hastighet i olika punkter och hur stora är g-krafterna? Sajten Lisebergs-Fysik innehåller mycket mer information bland annat om berg-och-dal banor.
innehåller mycket mer information bland annat om berg-och-dal banor.
För att få någon idé om storlekar, hastigheter etc, så har jag tittat på data från ett typexempel, länk 1.
En klassisk berg-och-dal bana fungerar så att vagnen dras upp till maxhöjden, och får sedan rulla i princip fritt ner och upp längs spåret. En förenklad version visas i figuren nedan. Vagnen startar med hastigheten 0 från punkt 1. Den accelereras nedför backen och går runt loopen. I verkligheten är naturligtvis loopen lite skruvad så att utgången är vid sidan av ingången.
Om vi antar att det inte finns några friktionsförluster kan vi använda energiprincipen för att räkna ut hastigheten i olika punkter: Totala energin = potentiell energi + kinetisk energi, Epot + Ekin = konstant.
Vagnens massa är M kg och vi räknar med tyngdaccelerationen g=10 m/s2. Radien på loopen är r=5 m.
I tabellen nedan listas värden för punkterna 1-4. De olika kolumnerna är:
Nr Punkt nummer
h Höjd över nollnivån (lägsta nivån [punkt 2] har h=0)
Epot Potentiell energi: Mgh
Ekin = 160M - Epot
v2 räknas ut från Ekin = Mv2/2
v räknas ut från v2
v2/r är centripetalaccelerationen i cirkelbanan i m/s2
C acc är centripetalaccelerationen uttryckt i g
Totalt g är totala g-kraften om vi även tar tyngdaccelerationen i beaktande, se vektordiagrammen längst ner i figuren. I stället för att involvera krafter är det i detta fallet enklare att räkna med accelerationer. Tyngkraften motsvaras då av en acceleration riktad rakt upp med beloppet 1g (de små svarta pilarna i figuren).
Vi kan räkna ut vad starthöjden skulle vara om centripetalaccelerationen i punkt 4 skulle vara g, dvs passagerarana skulle vara tyngdlösa:
v2/r = 10 -> v2 = 105 = 50
Ekin = Mv2/2 = M50/2 = 25M
Potentiella energin 25M motsvarar höjden 2.5 m, så starthöjden behöver vara 12.5 m för att centripetalaccelerationen i punkt 4 precis skall kompensera tyngaccelerationen.
Kommentarer
1 Maximala g-kraften i detta exemplet är 7.4 (i punkt 2) medan det i länk 1 sägs att den maximala g-kraften är 4. Ett skäl till avvikelsen kan vara att loopen inte vilar på lägsta nivån eller har större radie. Ett annat skäl är att man gör inte loopen cirkulär, utan päronformad med tjocka änden nedåt. Man får då en större krökningsradie där vagnen rör sig snabbast, och en mindre radie där den rör sig långsammast. Man jämnar alltså ut g-kraftena i loopen.
2 Det kan tyckas farligt att vagnen är upp-och-ner i toppen av loopen. I moderna anläggningar (men inte i den avbildade nedan) har man dubbla skenor både över och under hjulen. Om alltså vagnen skulle tappa fart så att den inte går tillräckligt snabbt på toppen, så skulle den ändå hänga kvar i de extra skenorna.
Se även Berg-_och_dalbana .
.
Ali! Jag hade lite svårt att förstå din fråga. Det du frågar om är nog en berg-och-dalbana (
Jag tänkte ta upp ett par saker av vad jag tror du frågade om: hur räknar man ut vagnens hastighet i olika punkter och hur stora är g-krafterna? Sajten Lisebergs-Fysik
För att få någon idé om storlekar, hastigheter etc, så har jag tittat på data från ett typexempel, länk 1.
En klassisk berg-och-dal bana fungerar så att vagnen dras upp till maxhöjden, och får sedan rulla i princip fritt ner och upp längs spåret. En förenklad version visas i figuren nedan. Vagnen startar med hastigheten 0 från punkt 1. Den accelereras nedför backen och går runt loopen. I verkligheten är naturligtvis loopen lite skruvad så att utgången är vid sidan av ingången.
Om vi antar att det inte finns några friktionsförluster kan vi använda energiprincipen för att räkna ut hastigheten i olika punkter: Totala energin = potentiell energi + kinetisk energi, Epot + Ekin = konstant.
Vagnens massa är M kg och vi räknar med tyngdaccelerationen g=10 m/s2. Radien på loopen är r=5 m.
I tabellen nedan listas värden för punkterna 1-4. De olika kolumnerna är:
Nr Punkt nummer
h Höjd över nollnivån (lägsta nivån [punkt 2] har h=0)
Epot Potentiell energi: Mgh
Ekin = 160M - Epot
v2 räknas ut från Ekin = Mv2/2
v räknas ut från v2
v2/r är centripetalaccelerationen i cirkelbanan i m/s2
C acc är centripetalaccelerationen uttryckt i g
Totalt g är totala g-kraften om vi även tar tyngdaccelerationen i beaktande, se vektordiagrammen längst ner i figuren. I stället för att involvera krafter är det i detta fallet enklare att räkna med accelerationer. Tyngkraften motsvaras då av en acceleration riktad rakt upp med beloppet 1g (de små svarta pilarna i figuren).
Nr h Epot Ekin v2 v v2/r C acc Totalt g
1 16 160M 0 0 0
2 0 0 160M 320 18 64 6.4 7.4
3 5 50M 110M 220 15 44 4.4 4.5
4 10 100M 60M 120 11 24 2.4 1.4
m J J (m/s)2 m/s m/s2
Vi kan räkna ut vad starthöjden skulle vara om centripetalaccelerationen i punkt 4 skulle vara g, dvs passagerarana skulle vara tyngdlösa:
v2/r = 10 -> v2 = 105 = 50
Ekin = Mv2/2 = M50/2 = 25M
Potentiella energin 25M motsvarar höjden 2.5 m, så starthöjden behöver vara 12.5 m för att centripetalaccelerationen i punkt 4 precis skall kompensera tyngaccelerationen.
Kommentarer
1 Maximala g-kraften i detta exemplet är 7.4 (i punkt 2) medan det i länk 1 sägs att den maximala g-kraften är 4. Ett skäl till avvikelsen kan vara att loopen inte vilar på lägsta nivån eller har större radie. Ett annat skäl är att man gör inte loopen cirkulär, utan päronformad med tjocka änden nedåt. Man får då en större krökningsradie där vagnen rör sig snabbast, och en mindre radie där den rör sig långsammast. Man jämnar alltså ut g-kraftena i loopen.
2 Det kan tyckas farligt att vagnen är upp-och-ner i toppen av loopen. I moderna anläggningar (men inte i den avbildade nedan) har man dubbla skenor både över och under hjulen. Om alltså vagnen skulle tappa fart så att den inte går tillräckligt snabbt på toppen, så skulle den ändå hänga kvar i de extra skenorna.
Se även Berg-_och_dalbana
 .
.
Länkar: http://www.rcdb.com/181.htm
/Peter E 2009-11-06
Hur påverkas vädret av corioliskraften?
Fråga:
Har en fråga om corioliskraften, eller snarare en bra förklaring på dess inverkan. Hur påverkas vädret egentligen? Eller är det en fråga för SMHI??
/jan g, Enskilda Gymnasiet, Stockholm 2010-11-13
Har en fråga om corioliskraften, eller snarare en bra förklaring på dess inverkan. Hur påverkas vädret egentligen? Eller är det en fråga för SMHI??
/jan g, Enskilda Gymnasiet, Stockholm 2010-11-13
Svar:
Jan! Det låter som en meteorologifråga, men corioliskraften orsakar ju rotationen hos lågtryck, högtryck och tropiska cykloner. Den påverkar även havsströmmar, passadvindar, jetströmmar, mm, som ju även de påverkar vädret. Se fråga [3160] för allmänt om corioliskraften.
Bilden nedan från Wikimedia Commons visar ett lågtryck över Island. I ett lågtryckssystem har man en luftström utifrån och inåt centrum. På grund av jordens rotation kommer på norra halvklotet en S-N gående luftström avlänkas mot öster och en N-S luftström att avlänkas mot väster, se CorioliseffektenCorioliskrafter_orsakade_av_jordens_rotation
visar ett lågtryck över Island. I ett lågtryckssystem har man en luftström utifrån och inåt centrum. På grund av jordens rotation kommer på norra halvklotet en S-N gående luftström avlänkas mot öster och en N-S luftström att avlänkas mot väster, se CorioliseffektenCorioliskrafter_orsakade_av_jordens_rotation . (Alltid påverkan åt höger på norra halvklotet, åt vänster på södra.) Ett lågtryck på norra halvklotet får alltså en rotation moturs. För storskaliga system är som synes corioliskraften mycket betydelsefull, och man måste ta hänsyn till den för väderprognoser. Se vidare SMHIs webbsajt, t.ex. länk 1 och 2 nedan.
. (Alltid påverkan åt höger på norra halvklotet, åt vänster på södra.) Ett lågtryck på norra halvklotet får alltså en rotation moturs. För storskaliga system är som synes corioliskraften mycket betydelsefull, och man måste ta hänsyn till den för väderprognoser. Se vidare SMHIs webbsajt, t.ex. länk 1 och 2 nedan.
Jan! Det låter som en meteorologifråga, men corioliskraften orsakar ju rotationen hos lågtryck, högtryck och tropiska cykloner. Den påverkar även havsströmmar, passadvindar, jetströmmar, mm, som ju även de påverkar vädret. Se fråga [3160] för allmänt om corioliskraften.
Bilden nedan från Wikimedia Commons
 . (Alltid påverkan åt höger på norra halvklotet, åt vänster på södra.) Ett lågtryck på norra halvklotet får alltså en rotation moturs. För storskaliga system är som synes corioliskraften mycket betydelsefull, och man måste ta hänsyn till den för väderprognoser. Se vidare SMHIs webbsajt, t.ex. länk 1 och 2 nedan.
. (Alltid påverkan åt höger på norra halvklotet, åt vänster på södra.) Ett lågtryck på norra halvklotet får alltså en rotation moturs. För storskaliga system är som synes corioliskraften mycket betydelsefull, och man måste ta hänsyn till den för väderprognoser. Se vidare SMHIs webbsajt, t.ex. länk 1 och 2 nedan.
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.
Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar

