Svar:
Energin kommer från bindningenergin. En massa som faller ner i ett svart hål binds av gravitationsfältet på samma sätt som en elektron binds i en atom. Elektronen skickar ut ljus när den övergår till lägre tillstånd. Det kan även infallande materia i ett svart hål göra genom kollisioner och uppvärmning, men en massa som rör sig snabbt kan även sända ut gravitationsvågor.

Den energi som sänds ut som elektromagnetisk strålning eller gravitationsvågor är förlorad, så massan av det kompakta objektet minskar med detta belopp. Låt oss titta lite närmare på energiförhållandena.

Klassiskt (Newton) är flykthastigheten från en massa M med radien R är lika med ljushastigheten c när

R = R_S = 2GM/c²

(flykthastigheten är v = (2GM/r)^1/2, se fråga [3782]).
Gravitationell bindningsenergi för en massa m vid ytan (kallas händelsehorisonten eller Schwarzschild-radien) av ett svart hål blir då

GMm/R_S = mc²/2

vilket är exakt halva vilomassan mc². Om man i stället använder den allmänna relativitetsteorin (vilket vi självklart mÃ¥ste göra) blir uttrycket för händelsehorisonten oförändrad men den gravitationella bindningsenergin blir lika med vilomassan mc².

Hur skall vi tolka detta? Om vi lÃ¥ter en massa m falla ner i ett svart hÃ¥l kan vi frigöra maximalt energin mc²/2. Resten kommer att försvinna som rödförskjutning. Ett svart hÃ¥l är alltsÃ¥ en mycket effektiv energikälla - fusion frigör t.ex. bara nÃ¥gon procent av vilomassan. Detta är orsaken till att man tror att de mest energetiska objekten vi känner till, t.ex. kvasarer, är svarta hÃ¥l. Om energin frigöres när massan är vid händelsehorisonten blir rödskiftet oändligt, och ingen energi slipper ut. Om vi emellertid lÃ¥ter energin strÃ¥la ut när massan är pÃ¥ väg ner, sÃ¥ kan en del av energin slippa ut - maximalt mc²/2.

Länk 1 innehåller information från en expert på området. Länk 2 är en användbar formelsamling för svarta hål. Se även Black_hole och Supermassive_black_hole.
/Peter E 2005-12-16

Svar:
Frida! Som fysikaliskt teori måste relativitetsteorin anses mycket etablerad. Detta gäller både relativitetsteorin, speciella
och relativitetsteorin, allmänna. Se
Special_theory_of_relativityConsequences_derived_from_the_Lorentz_transformation och
General_theory_of_relativityConsequences_of_Einstein's_theory
för några experimentella resultat som stöder den speciella och den allmänna relativitetsteorin.

Det universiella navigeringssystemet GPS (se Global_Positioning_System och nedanstående figur från Wikimedia Commons) med 24 satelliter i bana runt jorden på en höjd av 20000 km skulle helt enkelt inte fungera om man inte tog hänsyn till relativitetsteorierna.

Dels orsakar banrörelsen att den mycket exakta klockan i en satellit saktar sig 7 mikrosekunder per dygn pga den speciella relativitetsteorin. Eftersom satelliten befinner sig i ett svagare gravitationsfält går klockan 45 mikrosekunder per dygn snabbare. Nettokorrektionen 45-7=38 mikrosekunder per dygn appliceras genom att man justerar klockan att gå lite långsammare innan satelliten skickas upp. Man synkroniserar även alla klockorna med hjälp av klockor på marken. Se vidare länk 1.

Se vidare Special_relativity och General_relativity.

---

Tillägg 5/4/2011:

Uppskattning av effekterna

Konstanter:

Ljushastigheten: c = 3.0010⁸ m/s

Gravitationskonstanten: G = 6.67510^-11m³/(kg.s²)

Jordens massa: M = 5.97410²⁴ kg

Jordens radie: R = 6.3710⁶ m

GPS-satelliternas avstÃ¥nd frÃ¥n jordens centrum (20000 km över jordytan): R_GPS = 26.3710⁶ m

Speciell relativitet

Vi räknar från jordens centrum eftersom satelliterna går ganska högt och jordens rotationshastighet är liten (mindre än 500 m/s) jämfört med satelliternas hastighet.

Satellitens hastighet v ges av

mv²/R_GPS = mMG/(R_GPS)²

vilket blir

v = sqrt(MG/R_GPS) = sqrt(5.9710²⁴6.6710^-11/(26.36710⁶) = 3886 m/s

Klockan påverkas med g-faktorn (Special_relativityTime_dilation_and_length_contraction)

g = sqrt(1-(v/c)²) =
sqrt(1-(3886/300000000)^2) = 0.9999999999161055

Den relativa korrektionen blir

1 - g = 8.38910^-11

och korrektionen på ett dygn blir

8.38910^-11606024 = 7.2510^-6 s

eller c:a 7 mikrosekunder.

Allmän relativitet

Denna korrektion har att göra med att man mÃ¥ste bevara totala energin även i ett gravitationsfält, se frÃ¥ga [16989], stycket gravitationell rödförskjutning. För att bevara energiprincipen mÃ¥ste tiden i ett starkt gravitationsfält gÃ¥ lÃ¥ngsammare än i ett svagare. Tiden gÃ¥r alltsÃ¥ till synes snabbare i GPS satelliterna än pÃ¥ jordytan. Den relativa korrektionen ges av potentialskillnaden dividerat med viloenergin mc² (m är satellitens massa som kommer att försvinna i slututtrycket).

Om gravitationspotentialen är U(r) så gäller genom integration av gravitationskraften

U(r) = -mMG/r

Ändringen i potentiell energi om vi går från jordytan till satellitbanan blir

DU = -mMG/R_GPS -(-mMG/R) = -mMG(1/R_GPS -1/R)

Med insatta värden blir

DU = m4.714 10⁷

Om vi dividerar detta med viloenergin mc² fÃ¥r vi den relativa korrektionen till

5.237 10^-10

PÃ¥ ett dygn blir korrektionen

5.237 10^-10246060 s = 45.2 mikrosekunder

vilket stämmer bra med värdet ovan.

/Peter E 2006-04-27

Svar:
Hej Anna! Ställ en våg under klassrummet. Stäng dörrar och fönster och pumpa ut all luften. Du kommer att se en ändring i utslag som motsvarar luftens vikt :-).

Nej, så enkelt är det inte. Det är inte alls lätt att direkt mäta luftens densitet. Att luften väger något är lättare att visa, se fråga 14454 och länkarna nedan.

Låt oss i stället försöka räkna ut densiteten från andra storheter som är lättare att mäta. Det är ofta så i fysik att något kan vara svårt att mäta direkt medan det kan vara lätt att beräkna med kända fysikaliska lagar och andra storheter.

Vi använder den allmänna gaslagen:

pV = nRT

p = trycket, V = volymen, n = antal moler, R = allmänna gaskonstanten,

T = absoluta temperaturen

Om m är massan gas och M gasens molekylvikt kan vi skriva gaslagen

pV = (m/M)RT

Eftersom densiteten r = m/V får vi

r = pM/(RT)

Normaltrycket är 1.01310⁵ Pa (N/m²), luftens molekylvikt (en blandning av 80% N₂ och 20% O₂) är 28.8. Normal temperatur är 20^oC = 293 K.

Gaskonstanten är 8315 J kmol^-1 K^-1. Vi får då

r = 1.01310⁵28.8/(8315293) = 1.20 kg/m³. Om klassrummet är 10103 = 300 m³, väger luften 3001.20 = 360 kg, alltsÃ¥ lika mycket som fyra manliga normallärare!
/Peter E 2007-02-28

Svar:
Det är så att man inte skall kunna nalla av glasspinnarna hela tiden :-).

Det är lufttrycket som håller igen dörren. Avkylningen av luften i frysen orsakar ett undertryck. Efter en stund (några minuter) utjämnas detta undertryck eftersom frysen inte är helt tät. Tryckutjämningen ger upphov till ett pysande ljud. Undertrycket ger upphov till en kraft som stänger dörren ordentligt.

Låt oss göra en uppskattning av hur stor kraften kan bli. Vi använder den allmänna gaslagen:

pV = nRT

p = trycket, V = volymen, n = antal mol, R = allmänna gaskonstanten,

T = absoluta temperaturen

Anta att rumstemperaturen är 20^oC och temperaturen i frysen är -20^oC. I gaslagen skall vi använda absoluta temperaturer, så temperaturerna blir T_rum=273+20=293 K och T_frys=273-20=253 K.

Vi kan skriva gaslagen som

p = (nR/V)T = konstantT

Om n är antal mol gas i frysen när dörren precis stängs, så är n och naturligtvis även V konstanta. Vi får

p_frys = konstantT_frys

p_rum = konstantT_rum

Varav följer

p_frys = (T_frys/T_rum)p_rum

Normaltrycket i rummet är ungefär 10⁵ Pa (N/m²) varför vi fÃ¥r

p_frys = (253/293)10⁵ = 86348 Pa

Undertrycket blir alltså 100000-86348 = 14000 Pa

Om dörrens yta är 1 m² sÃ¥ är alltsÃ¥ kraften frÃ¥n övertrycket hela 14000 N. Detta motsvarar en vikt pÃ¥ 1400 kg!

Detta låter ganska mycket (vi borde inta alls kunna få upp dörren), men vi har räknat lite väl optimistiskt. För det första hinner inte all luft i den kalla frysen bytas ut. Om vi har dörren öppen så länge att all luft bytts ut, kommer det i stället ta mycket lång tid att kyla ner luften, och rumsluft kommer att läcka in. Dessutom är handtaget placerat i kanten av dörren och inte i mitten. Hävstångslagen ger då att den erforderliga kraften blir hälften så stor.

En riktigt gammal horisontell frys ger inte stor effekt eftersom den kalla luften stannar i frysen - kall luft har ju högre densitet. En modern frys med plastbackar ger även den liten effekt eftersom ingen kall luft kommer in. En halvgammal öppen frys ger bäst effekt - den kalla luften formligen rinner ut när man öppnar dörren!

Enkelt experiment:

För att illustrera att kall luft ger undertryck: Sätt på korken på en tom PET-flaska och lägg flaskan i frysen. När flaskan är kall tar man ut den och lossar försiktigt på korken. Vad händer och varför?
/Peter E 2007-05-05

Svar:
Hej Mia! Jodå, med tillräckligt många ballonger kommer flickan att sväva iväg. Nedan finns en överslagsräkning hur mycket ballonger det krävs. Räkningarna är inte helt triviala, men 2:a klassarna får lita på att räkningarna är korrekta.

Enligt Arkimedes princip är lyftkraften lika med den undanträngda luftens vikt:

lyftkraft = volym(luftens densitet)g

Heliumet i ballongen ger en nedåtriktad kraft, så nettolyftkraften blir

nettolyftkraft = volym(luftens densitet - heliumets densitet)g

Vi har här bortsett från vikten hos ballongmaterialet (gummit). Tyngdkraften på en 25 kg flicka är

F = mg = 25g

Om vi sätter denna lika med nettolyftkraften får vi med V som totala ballongvolymen och d som densiteter:

25g = V(d_luft - d_helium)g

dvs

V = 25/(d_luft - d_helium) m³

Luftens densitet vid 20^oC är c:a 1.2 kg/m³. Vad är dÃ¥ heliums densitet vid samma temperatur? Enligt gaslagen, allmänna innehÃ¥ller en viss volym av en gas lika mÃ¥nga mol oberoende av vilken gas det är. Densiteten skalar sig alltsÃ¥ som molekylvikten. Heliums molekylvikt är 4 och luftens 28.8. Heliums densitet blir alltsÃ¥

d_helium = (4/28.8)1.2 = 0.17 kg/m³

Volymen som krävs blir alltså

V = 25/(1.2 - 0.17) m³ = 24 m³

Om en klotformig ballong har diametern 40 cm så blir radien r 0.2 m och volymen

4pr³/3 = 4p0.2³/3 = 0.034 m³

Det krävs alltså 24/0.034 = c:a 700 ballonger!

Vi har här bortsett från två saker: vikten hos ballongmaterialet och det faktum att man om ballongen är gjord av ett elastiskt material får lite högre tryck och därmed högre densitet innuti ballongen. Detta därför att gummits elasticitet orsakar en kraft som trycker ihop den inneslutna gasen. Man kan komma ifrån denna effekt om man använder sig av icke elastiska plastballonger.

Ursäkta att detta blev lite tekniskt, men om man vill ha ett kvantitativt svar så går det nog inte att göra enklare. Det som behövs är alltså två enkla fysikaliska lagar, Arkimedes princip och Den allmänna gaslagen, som båda sedan länge är väl etablerade både experimentellt och teoretiskt.

Se även länk 1.
/Peter E 2007-09-12

Svar:
Malin! Du har bra idéer om orsaken. Framför allt två effekter kan spela in. Den första effekten om man värmer burken snabbt och den andra om man värmer den länge.

Termisk expansion (att material utvidgar sig när temperaturen blir högre): Metaller utvidgar sig mer än glas, se tabell i artikeln Coefficient_of_thermal_expansion. Lägg märke till att den öppna delen av locket expanderar som om den vore gjord av metallen. Utvidgningskoefficienten för hål är alltså lika med den för omgivningen, se länk 1 (stycket "Thermal expansion : expanding holes") för bevis. Dessutom leder metall värme bra, medan glas leder värme dåligt. Locket blir alltså varmare än glaset, vilket förhöjer effekten att locket expanderar relativt burken. Det blir då lättare att lossa locket dels för att kontakten med burken blir mindre, och dels för att eventuella tryckskillnader kan utjämnas (se nedan).

Att ett hål expanderar som omgivningen används i mekanisk industri för något som kallas krympförband (Shrink-fitting).

Undertryck: Locket sätts på vid en förhöjd temperatur. För en ideal gas gäller den ideala gaslagen (se fråga [15294] eller Gas_laws) att

pV = nRT

Vid konstant volym V och konstant mängd gas (n) är tryckändringen Dp proportionellt mot temperaturändringen DT. Vi får

Dp/p = DT/T

Om omgivningstemperaturen är 20^oC = 293 K och temperaturen när locket sattes på 100^oC får vi

Dp = p80/293 = 1.01310⁵80/293 = 28000 N/m² (pascal, Pa)

Om locket har en radie pÃ¥ 3 cm är ytan 3²p, dvs c:a 30 cm². Totala kraften pÃ¥ locket blir dÃ¥

0.003028000 = 84 N. Detta motsvarar kraften som krävs för att lyfta c:a 8 kg, alltså en ganska stor kraft.

Om man värmer upp burken genom att hålla den länge under varmvattenskranen reduceras tryckskillnaden och därmed kraften. Observera alltså att tricket att hålla burken under varmvattenkranen hjälper för båda förklaringarna ovan!

Mikroskopisk förståelse av gaslagen:

Man kan förstå varför en viss mängd luft ger lägre tryck vid lägre temperatur. Temperatur är ett mått på molekylernas medelhastighet - om vi har låg temperatur så rör sig molekylerna långsamt. De kommer därför att kollidera med väggarna mindre ofta och mindre våldsamt än om temperaturen är hög. Det är just molekylernas kollektiva effekt på väggarna som makroskopiskt (i vår värld, till skillnad från molekylernas mikroskopiska värld) uppfattas som tryck.
/Peter E 2008-02-22

Svar:
Ljuset följer den snabbaste vägen som i ett gravitationsfält inte är en rät linje, se fråga [17427].

Det är ingalunda trivialt att räkna ut avböjningen. Man måste använda hela formalismen för den allmänna relativitetsteorin, se Two-body_problem_in_general_relativityApproximate_formula_for_the_bending_of_light.

Avböjningen vid solranden ges av uttrycket

df = 4GM/c²b

där G är gravitationskonstanten G = 6.674 10^-11 m³s^-2kg^-1

M är solens massa M = 1.989 10³⁰ kg

c är ljushastigheten c = 2.998 10⁸ m/s

b är solens radie b = 6.955 10⁸ m

Låt oss innan vi räknar ut df se vad den har för dimension

[df] = [m³s^-2kg^-1][kg]/([m²/s²][m]) = 1

dvs dimensionslöst som sig bör för en vinkel i radianer.

Vi får

df = 8.494 10^-6 radianer

Men 1 bågsekund är

2p/(3606060) = 4.848 10^-6 radianer.

Avböjningen i bågsekunder blir alltså

df = (8.494 10^-6)/(4.848 10^-6) = 1.75"

För att räkna på ett annat objekt, t.ex. ett svart hål, byter man bara ut massan M och radien b i formeln ovan.

Eddingtons mätningar vid solförmörkelsen 1919, nedanstående bild, (se Tests_of_general_relativity och länk 1) har ifrågasatts, men resultatet av mätningen har senare bekräftats. I vilket fall som helst innebar mätningarna en omedelbar acceptans av den allmänna relativitetsteorin från alla utom möjligen nobelpris-kommitteen.

/Peter E 2009-03-23

Svar:
Marianne! Vid tillräckligt högt tryck går säkert burken sönder. Detta är ingen myt. Låt oss titta på vad som händer med trycket.

Om det bara finns gas i burken (dvs burken är nästan tom) kan man tillämpa allmänna gaslagen (gaslagen, allmänna, Ideala_gaslagen):

pV = nRT

(p tryck i Pa, V volym i m³, n antal mol gas, R gaskonstanten 8.314 J/(molK), T absoluta temperaturen i K)

Trycket ökar alltså med absoluta temperaturen för konstant volym. Om vi utgår från 20 grader som normaltemperatur så ökar trycket vid 50 grader med faktorn (50+273)/(20+273) = 1.10, alltså med 10%. Vi måste gå till över 300 grader för att trycket skall fördubblas. Så om burken innehåller en ideal gas (allt i burken är i gasform) är det ingen fara, eftersom burken bör tåla ganska höga temperaturer.

Men en sprayburk innehåller emellertid inte bara gas utan även vätska. I en genomskinlig behållare (t.ex. en cigarrettändare, se fråga 16119 nedan) kan man se detta. Om man skakar en spayflaska försiktigt, kan man känna att en vätska "skvalpar omkring" inne i burken. Problemet är då inte lösbart med antagandet om en ideal gas, utan man måste ta hänsyn till vätskans Ångtryck.

Ångtrycket är relaterat till vätskans kokpunkt - kokpunkten vid 1 atmosfärs tryck är den temperatur vid vilken vätskans ångtryck är 1 atm. Bilden nedan från Wikimedia Commons visar ångtrycket för några vätskor som funktion av temperaturen. De olika ämnena i figuren uppför sig ganska lika, med skillnaden att kokpunkten är mycket olika. Om vi tar neo-Pentan (mörkgrön kurva) som exempel ser vi för det första att kokpunkten vi trycket 1 atm är 10 grader. För några olika temperaturer kan vi läsa av följande från kurvan:

10^oC - 1 atm

20^oC - 1.4 atm

50^oC - 3.5 atm

80^oC - 8 atm

Vi ser alltså att trycket ökar mycket med förhöjd temperatur.

Vad kan vi dra för slutsatser? För det första att Mythbusters test visade att tillverkarnas rekommenderade högsta temperatur var konservativt säker. Det framgår inte hur högt upp i temperatur man gick vid testen. För det andra kan man dra slutsatsen att om burken bara innehåller gas, så tål den ganska höga temperaturer. Om burken emellertid även innehåller vätska ökar trycket mycket snabbt med temperaturen, så burken kommer till slut att explodera.

/Peter E 2009-10-22

Svar:
Ali! Det var många svåra frågor. Låt oss börja med partikel-egenskaper. Jag tycker inte man skall föreställa sig en foton varken som en partikel eller en våg. En foton är en foton som lånat egenskaper både från partiklar och vågor.

Fotonens massa: Fotonen har energin E=hv. Eftersom energi och massa är ekvivalenta (E=mc²), sÃ¥ har fotonen massa. Man kan emellertid inte tala om fotonens vilomassa eftersom begreppet en stillastÃ¥ende foton saknar mening.

Experimentella bevis för att fotonen saknar vilomassa kommer bland annat frÃ¥n det faktum att den elektrostatiska kraften (Coulombs lag, som ju förklaras genom ett utbyte av virtuella fotoner) varierar som 1/r² En utbytespartikel med ändlig vilomassa hade givit ett annat avstÃ¥ndsberoende.

Se fråga [16939] för mer om historien bakom fotonbegreppet och länk 1 för en mer detaljerad framställning. Wikipedia-artikeln Photon är mycket bra, medan den svenska versionen är OK men inte särskilt omfattande: Foton.

Fotoner påverkas på två sätt av gravitationsfält:

1 Avböjning, t.ex. vid passage nära solen. Detta har behandlats ganska detaljerat i fråga [16021].

2 Gravitationell rödförskjutning.

Till skillnad frÃ¥n avböjning sÃ¥ kräver faktiskt en tillfredsställande behandling av gravitationell rödförskjutning bara enkel klassisk fysik och speciella relativitetsteorins E=mc². Börja med att studera den enkla animeringen under länk 2!

Den potentiella energin hos elektronerna i övre läget är (mgh)

2m_egH

Om vi förlänger med c² fÃ¥r vi

2m_ec²(gH/c²) = E_foton(gH/c²)

Vi fÃ¥r det relativa skiftet för höjdskillnaden 22.5 m (ref. ¹):

DE_foton/E_foton = gH/c² = 9.80322.5/(2.99810⁸)² = 2.454 10^-15

Det relativa skiftet har uppmätts (ref. ¹) med hjälp av mössbauerspektroskopi (se nedan) för 14.4 keV fotoner frÃ¥n ⁵⁷Co-sönderfall. Det uppmätta resultatet 2.451 10^-15 (med c:a 1% osäkerhet) är i bra överensstämmelse med detta.

Observera att det enda antagande vi gör är energins bevarande, vilket är en av fysikens grundläggande och mest etablerade lagar.

Observera även att man kan se skiftet till större våglängd (och därmed lägre frekvens) när fotonerna går uppåt är ekvivalent med att klockan går långsammare i ett starkare gravitationsfält.

Liknande experiment med hjälp av satelliter som sänder ut en mycket välbestämd frekvens har bekräftat Einsteins teori med en noggranhet bättre än 1 del pÃ¥ 10⁴.

Se vidare General_relativity, Gravitational_redshift och Pound-Rebka_experiment.

Se även http://fy.chalmers.se/~f1xjk/FysikaliskaPrinciper/FOREL.lp2/F16/F16.html

Mössbauerspektroskopi

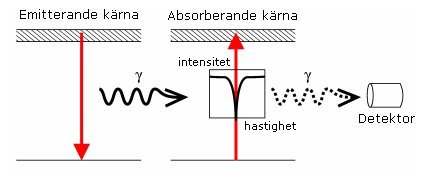
Mössbauer-effekten är rekylfri emission och absorption av gammastrålning från atomkärnor. När en atomkärna utsänder ett gammakvantum förloras i en del av energin till kärnans rekyl liksom vid absorption i en absorberande kärna. Detta eftersom både energi och rörelsemängd måste bevaras i processen.

I mössbauereffekten elimineras förlusterna dels genom att de radioaktiva kärnorna sitter i en kristall som tar upp rekylen, så att emission och absorption kan ske vid samma energi och dels genom att man kan kompensera energiförlusten genom att låta den utsändande kärnan röra sig.

Eftersom rekylen är mycket liten räcker det med en mycket måttlig hastighet på några mm/sekund, se nedanstående bild där det lilla diagrammet är en plot av ett mössbauerspektrum med hastighet på den horisontella axeln och observerad intensitet på den vertikala. Dippen i spektrum reflekterar det exciterade tillståndets vidd DE. Vidden är relaterad till tillståndets livslängd enligt Heisenbergs obestämdhetsrelation:

DE·Dt = h / 4p ~ 10^-34 Js

Se vidare Mössbauer_spectroscopy och mössbauer-effekten. Se även fråga [14685].
____________________________________________________________

¹ Pound and Snider, Physical Review Letters Vol 13, 18 (1964) 539

/Peter E 2010-03-15

Svar:
Frank! Det var Galileo Galilei som först utförde experiment och resonerade om detta, se Galileo_GalileiPhysics. Einstein använde ekvivalensen mellan acceleration och gravitation som ett grundantagande för sin allmänna relativitetsteori. Av detta följer direkt att alla kroppar faller lika snabbt i ett tyngdkraftfält. Man kan alltså byta ut ett tyngdkraftfält med en acceleration i motsatt riktning.

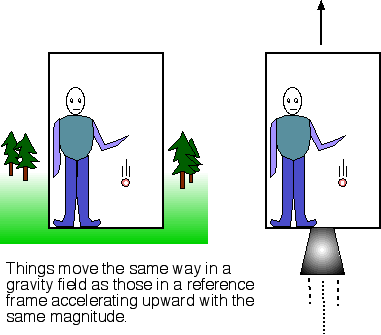
Låt oss säga du står i en hiss som befinner sig på marken (se nedanstående bild från länk 1). Du släpper ett föremål som faler nedåt. På grund av ovanstående ekvivalensprincip kan vi byta ut tyngdkraftfältet mot en lika stor acceleration uppåt. Det är uppenbart i detta fall (till höger i figuren) att fallhastigheten är helt oberoende av massan hos föremålet eftersom det ju står stilla (påverkas inte av någon kraft) medan hissen och du (som står på golvet) accelererar uppåt.

Se fråga [13663] för en kul demonstration.

Tillägg om ekvivalensprincipen

Engelska Wikipedia definierar ekvivalensprincipen som (Equivalence_principle):

In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's observation that the gravitational "force" as experienced locally while standing on a massive body (such as the Earth) is actually the same as the pseudo-force experienced by an observer in a non-inertial (accelerated) frame of reference.

Ekvivalensprincipen förekommer även i en svagare form i klassisk newtonsk fysik: ekvivalensen mellan tung och trög massa, dvs att massan m som förekommer i uttrycket

F = m a

är samma som förekommer i Newtons gravitationslag

F = G M m/r²

dvs accelerationen a ges av

a = G M/r²

oberoende av m.

Av detta följer att alla föremål faller med samma acceleration i ett gravitationsfält (bortsett från luftmotståndet).

Länk 2 innehåller Galileis teoretiska argumentation för ekvivalensprincipen. Se A Cultural History of Gravity and the Equivalence Principle för diskussion om tidigare funderingar (den Bysantinske filosofen Iohannes Philiponus).

/Peter E 2010-09-05