Vill du ha ett snabbt svar - sök i databasen:
600 frågor / svar hittades
Jag har svårt att förstå varför gas har en vikt
Gymnasium: Kraft-Rörelse - barometerformeln [13693]
Fråga:
Jag har svårt att förstå varför gas har en vikt.
Tankeexperiment:
Om man för in en gasatom i en sluten vakuumbehållare som står på en våg så kommer ju vågen (i princip) att att visa att vikten ökar.
Lite flummigt tänkande.
Jag tycker ju att gasmolekylens krockar med behållarens botten och ovansidan borde vara lika många och därför borde nettokrafterna ta ut varandra.
Att en vätska eller fast ämne väger är ju lättare att förstå eftersom atomerna ligger på botten och "väger", men en gasmolekyl den "svävar i tomma intet"
Mycket tacksam för svar då jag undrat över frågan under lång tid och skolans fysiklärare har inte kunnat ge någon förklaring.
/Mats O, Gudlav Bilderskolan, Sollefteå 2005-01-20
Jag har svårt att förstå varför gas har en vikt.
Tankeexperiment:
Om man för in en gasatom i en sluten vakuumbehållare som står på en våg så kommer ju vågen (i princip) att att visa att vikten ökar.
Lite flummigt tänkande.
Jag tycker ju att gasmolekylens krockar med behållarens botten och ovansidan borde vara lika många och därför borde nettokrafterna ta ut varandra.
Att en vätska eller fast ämne väger är ju lättare att förstå eftersom atomerna ligger på botten och "väger", men en gasmolekyl den "svävar i tomma intet"
Mycket tacksam för svar då jag undrat över frågan under lång tid och skolans fysiklärare har inte kunnat ge någon förklaring.
/Mats O, Gudlav Bilderskolan, Sollefteå 2005-01-20
Svar:
Barometerformeln säger att
p = p0 - rgh
där p är trycket vid höjden h
g är tyngdaccelerationen
r är gasens densitet
Om lådan finns i ett rum med samma gas och tryck som inuti lådan, så kommer gasen inte att utöva någon netto-kraft. Detta därför att övertrycket på lådans golv och undertrycket på lådans tak kompenseras av motsvarande tryck på lådans utsidor. Om man däremot pumpar ut gasen ur lådan, så kommer man att få en nettokraft uppåt som motsvarar den undanträngda gasens vikt - Arkimedes princip.
Det är ingen skillnad på om det är en gas eller en vätska. Trycket på botten blir större är trycket på locket med ett belopp som svarar mot massangh.
Föreställ dig gasen som en samling bollar som studsar omkring. Tänk dig en boll som studsar i golvet med en viss hastighet. När bollen kommit upp till höjden h har den mer potentiell energi och därmed mindre rörelseenergi. Bollarna rör sig alltså i medeltal långsammare vid taket, vilket betyder att de utövar mindre tryck. Det är alltså en tryckskillnad även om bollarna inte rör vid varandra!
Om höjden h inte är försumbar kommer densiteten att avta med h. Om man tar hänsyn till detta får man integrera. Uttrycket blir då exponentialuttrycket längst ner i figuren.
Barometerformeln säger att
p = p0 - rgh
där p är trycket vid höjden h
g är tyngdaccelerationen
r är gasens densitet
Om lådan finns i ett rum med samma gas och tryck som inuti lådan, så kommer gasen inte att utöva någon netto-kraft. Detta därför att övertrycket på lådans golv och undertrycket på lådans tak kompenseras av motsvarande tryck på lådans utsidor. Om man däremot pumpar ut gasen ur lådan, så kommer man att få en nettokraft uppåt som motsvarar den undanträngda gasens vikt - Arkimedes princip.
Det är ingen skillnad på om det är en gas eller en vätska. Trycket på botten blir större är trycket på locket med ett belopp som svarar mot massangh.
Föreställ dig gasen som en samling bollar som studsar omkring. Tänk dig en boll som studsar i golvet med en viss hastighet. När bollen kommit upp till höjden h har den mer potentiell energi och därmed mindre rörelseenergi. Bollarna rör sig alltså i medeltal långsammare vid taket, vilket betyder att de utövar mindre tryck. Det är alltså en tryckskillnad även om bollarna inte rör vid varandra!
Om höjden h inte är försumbar kommer densiteten att avta med h. Om man tar hänsyn till detta får man integrera. Uttrycket blir då exponentialuttrycket längst ner i figuren.
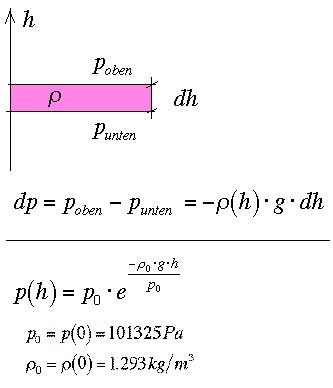
Laboration om tröghetslagen och friktion
Fråga:
I ett laboration som vi gjorde i skolan, vi skulle visa att Kraftekvationen gäller där vi använde tyngden av massan m för att sätta fart på vagnen med massan M. Med hjälp av två ljusportar bestämde vi vagnens hastigheter vid två tillfällen. Sedan bestämde vi värden på den accelererande kraften (dragkraften) samt produkten av massan och accelerationen. Vi fick då olika värden på kraften och produkten av massa och accelerationen. Min fråga är att vilket är förklaringen till avvikelsen mellan värden på kraften och produkten av massan och accelerationen??? Och hur kan man redovisa för de korrigeringar som bör göras??
/Sara H, Birgitta, Linköping 2005-02-24
I ett laboration som vi gjorde i skolan, vi skulle visa att Kraftekvationen gäller där vi använde tyngden av massan m för att sätta fart på vagnen med massan M. Med hjälp av två ljusportar bestämde vi vagnens hastigheter vid två tillfällen. Sedan bestämde vi värden på den accelererande kraften (dragkraften) samt produkten av massan och accelerationen. Vi fick då olika värden på kraften och produkten av massa och accelerationen. Min fråga är att vilket är förklaringen till avvikelsen mellan värden på kraften och produkten av massan och accelerationen??? Och hur kan man redovisa för de korrigeringar som bör göras??
/Sara H, Birgitta, Linköping 2005-02-24
Svar:
Hej Sara!
Ni har gjort ett experiment för att undersöka tröghetslagen F=ma, Newtons andra rörelselag. Med de givna förutsättningarna väntar man sig idealiskt följande samband:
F = mg = (m+M)a
där mg är den accelererande kraften och m+M är massan som accelereras.
För det första är alla mätningar behäftade med osäkerheter (i bland oegentligt kallade fel). För försöket ni gjort kommer det sedan säkert in en systematisk felkälla: friktionen. Om ni kan mäta denna på ett oberoende sätt skulle ni kunna korrigera för den.
Möjligen skulle man till en del kunna få en uppfattning om friktionen genom att variera tyngden m. I en första approximation beror friktionen av M (proportionell mot normalkraften), och bör alltså bli av relativt mindre betydelse om m (och därmed kraften) ökas.
På min begäran skickade du följande mätdata (presentationen något modifierad):
Utan friktion väntar vi oss att accelerationen a ges av
a = g/(1+M/m)
Tar vi hänsyn till en friktionskraft fMg får vi
a = (g-fMg/m)/(1+M/m)
Detta samband är plottat i nedanstående figur för f=0.5 och 1%.
Dina uppmätta data uppvisar lite spridning, men jag tycker att de stämmer relativt bra med kurvan för f=0.5%. Olika värden på M har markerats med olika symboler, men jag kan inte se någon systematik.
För att förbättra experimentet skulle man kunna ta fler mätpunkter för att få en bättre uppfattning om de tillfälliga mätfelen i bestämningen av accelerationen.
Hej Sara!
Ni har gjort ett experiment för att undersöka tröghetslagen F=ma, Newtons andra rörelselag. Med de givna förutsättningarna väntar man sig idealiskt följande samband:
F = mg = (m+M)a
där mg är den accelererande kraften och m+M är massan som accelereras.
För det första är alla mätningar behäftade med osäkerheter (i bland oegentligt kallade fel). För försöket ni gjort kommer det sedan säkert in en systematisk felkälla: friktionen. Om ni kan mäta denna på ett oberoende sätt skulle ni kunna korrigera för den.
Möjligen skulle man till en del kunna få en uppfattning om friktionen genom att variera tyngden m. I en första approximation beror friktionen av M (proportionell mot normalkraften), och bör alltså bli av relativt mindre betydelse om m (och därmed kraften) ökas.
På min begäran skickade du följande mätdata (presentationen något modifierad):
m (kg) M (kg) a (m/s2) M/m
0.04 0.353 1.01 8.83
0.05 0.353 1.13 7.06
0.02 0.353 0.468 17.7
0.02 0.516 0.332 25.8
0.02 0.580 0.224 29.0
0.03 0.353 0.693 11.8
0.03 0.522 0.481 17.4
Utan friktion väntar vi oss att accelerationen a ges av
a = g/(1+M/m)
Tar vi hänsyn till en friktionskraft fMg får vi
a = (g-fMg/m)/(1+M/m)
Detta samband är plottat i nedanstående figur för f=0.5 och 1%.
Dina uppmätta data uppvisar lite spridning, men jag tycker att de stämmer relativt bra med kurvan för f=0.5%. Olika värden på M har markerats med olika symboler, men jag kan inte se någon systematik.
För att förbättra experimentet skulle man kunna ta fler mätpunkter för att få en bättre uppfattning om de tillfälliga mätfelen i bestämningen av accelerationen.

Förklara begreppet potential!
Gymnasium: Kraft-Rörelse - potential/potentiell energi [13821]
Fråga:
Jag frågade förut den här frågan: Ökar eller minskar den potentiella energin när en laddning flyttar sig mot den elektriska kraften?
Men nu har jag en annan fråga om det.. Varför minskar den potentiella energin när en laddning flyttar sig med den elektriska kraften?
/Diar R, Bersilius, Linköping 2005-02-25
Jag frågade förut den här frågan: Ökar eller minskar den potentiella energin när en laddning flyttar sig mot den elektriska kraften?
Men nu har jag en annan fråga om det.. Varför minskar den potentiella energin när en laddning flyttar sig med den elektriska kraften?
/Diar R, Bersilius, Linköping 2005-02-25
Svar:
Enligt Nationalencyklopedin definieras
definieras potential som
det arbete som krävs för att förflytta en massenhet, en positiv enhetsladdning eller en magnetisk enhetspol från oändligt avstånd från ett konservativt kraftfälts källor (jfr konservativ kraft) till en punkt i kraftfältet (gravitationsfält, elektrostatiskt eller magnetiskt fält).
Enkonservativ kraft är en kraft som har egenskapen att
arbetet den uträttar är oberoende av vägen och endast beror av begynnelse- och slutläget. Gravitationskraft och coulombkraft är exempel på konservativa krafter, medan friktionskraften är exempel på en icke-konservativ eller dissipativ kraft.
Man kan alltså definiera begreppen potentiell energi och potential om man har att göra med en konservativ kraft. Eftersom många kraftverkningar inom fysiken är konservativa är begreppet potential mycket viktigt.
I en dimension är sambandet mellan potentialen U(x) och kraften som utövas
F(x) = -dU(x)/dx
Observera minustecknet! Det betyder att kraften är riktad mot potentialökningen.
För ett föremål som befinner sig i en potential (t.ex. en satellit i jordens gravitationsfält) gäller att summan av den potentiella energin U och den kinetiska energin K (rörelseenergin) är konstant:
Total energi (konstant) = U + K = U + mv2/2
där v är hastigheten.
Låt oss som ett enkelt exempel på tillämpning av potential räkna ut hur fort ett föremål faller när det träffar marken från en höjd av 100 (h) meter om vi kan bortse från luftmotståndet (se bilden nedan). Vi antar att förmålets massa är m, men detta kommer inte att ha någon betydelse för slutresultatet. Ändringen i den potentiella energin är enligt ovan (kraften F är konstant eftersom h är litet jämfört med jordens radie):
F(x)Dx = -DU(x) eller -DU = mgh
om den potentiella energin vid marken sättes lika med 0. Om hastigheten vid höjden h är noll är hela energin potentiell energi vid höjden h och hela energin kinetisk energi vid marken. Vi får då
mgh = mv2/2
och
v = sqrt(2gh) = sqrt(29.81100) = sqrt(1962) = 44 m/s
Se vidarePotential_energy och länken nedan.
Observera att man i kvantmekaniken aldrig talar om krafter - man använder sig av potentialer.
Enligt Nationalencyklopedin
det arbete som krävs för att förflytta en massenhet, en positiv enhetsladdning eller en magnetisk enhetspol från oändligt avstånd från ett konservativt kraftfälts källor (jfr konservativ kraft) till en punkt i kraftfältet (gravitationsfält, elektrostatiskt eller magnetiskt fält).
En
arbetet den uträttar är oberoende av vägen och endast beror av begynnelse- och slutläget. Gravitationskraft och coulombkraft är exempel på konservativa krafter, medan friktionskraften är exempel på en icke-konservativ eller dissipativ kraft.
Man kan alltså definiera begreppen potentiell energi och potential om man har att göra med en konservativ kraft. Eftersom många kraftverkningar inom fysiken är konservativa är begreppet potential mycket viktigt.
I en dimension är sambandet mellan potentialen U(x) och kraften som utövas
F(x) = -dU(x)/dx
Observera minustecknet! Det betyder att kraften är riktad mot potentialökningen.
För ett föremål som befinner sig i en potential (t.ex. en satellit i jordens gravitationsfält) gäller att summan av den potentiella energin U och den kinetiska energin K (rörelseenergin) är konstant:
Total energi (konstant) = U + K = U + mv2/2
där v är hastigheten.
Låt oss som ett enkelt exempel på tillämpning av potential räkna ut hur fort ett föremål faller när det träffar marken från en höjd av 100 (h) meter om vi kan bortse från luftmotståndet (se bilden nedan). Vi antar att förmålets massa är m, men detta kommer inte att ha någon betydelse för slutresultatet. Ändringen i den potentiella energin är enligt ovan (kraften F är konstant eftersom h är litet jämfört med jordens radie):
F(x)Dx = -DU(x) eller -DU = mgh
om den potentiella energin vid marken sättes lika med 0. Om hastigheten vid höjden h är noll är hela energin potentiell energi vid höjden h och hela energin kinetisk energi vid marken. Vi får då
mgh = mv2/2
och
v = sqrt(2gh) = sqrt(29.81100) = sqrt(1962) = 44 m/s
Se vidare
Observera att man i kvantmekaniken aldrig talar om krafter - man använder sig av potentialer.

Apan på repet
: Kraft-Rörelse - potential/potentiell energi [13874]
Fråga:
Hej,
Vi är några kompisar som tagit ett IQ-test på nätet och nu är djupt oense om en fråga. Eftersom sidan inte gav några svar vänder vi oss nu till er eftersom frågan vållar oss huvudbry.
Ett rep hänger i en fullständigt friktionsfri trissa. På ena sidan hänger en apa och på andra sidan hänger en vikt. Det råder jämvikt, men sedan bestämmer sig apan för att klättra uppför repet. Vad händer då?
Står vikten stilla, sjunker den, eller stiger den? Vi står här med fullständigt olika åsikter, men finner inga svar. Har ni något?
/Daniel W, Ystad 2005-03-12
Hej,
Vi är några kompisar som tagit ett IQ-test på nätet och nu är djupt oense om en fråga. Eftersom sidan inte gav några svar vänder vi oss nu till er eftersom frågan vållar oss huvudbry.
Ett rep hänger i en fullständigt friktionsfri trissa. På ena sidan hänger en apa och på andra sidan hänger en vikt. Det råder jämvikt, men sedan bestämmer sig apan för att klättra uppför repet. Vad händer då?
Står vikten stilla, sjunker den, eller stiger den? Vi står här med fullständigt olika åsikter, men finner inga svar. Har ni något?
/Daniel W, Ystad 2005-03-12
Svar:
Hej Daniel och ni andra oense!
Så detta problemet var del av IQ-testen? I så fall klarar jag i varje fall en fråga :-).
Försöksuppställning: se nedanstående bild.
Om trissan är friktionsfri och repet viktlöst, så kan vi först konstatera att apan och vikten har samma massa eftersom dom utövar samma kraft (jämviktsvillkoret). Låt oss anta att denna massa är m. Tyngkraften blir då mg, och denna kompenseras med spänningskraften i repet: F=mg.
För att apan skall kunna klättra måste den utöva en ytterligare kraft uppåt (se nedanstående diskussion). Denna kraft fortplantar sig i repet och kommer även att påverka vikten. Eftersom massan är lika, så kommer vikten att exakt spegla apans rörelser. Så om apan klättrar höjden h, så kommer vikten att höjas lika mycket.
Låt oss diskutera några aspekter på tankeexperimentet.
1 Eftersom vikten sitter fast i repet kommer detta att förskjutas med beloppet h. Apan måste alltså klättra sträckan 2h i förhållande till repet.
2 Man kanske skulle kunna luras av att tillämpa energiprincipen och säga att om apan klättrar höjden h så kompenseras detta med att vikten sjunker med samma belopp. Detta är naturligtvis fel, eftersom det är inget som säger att den potentiella energin i systemet skall bevaras. Apan tar av sitt förråd av kemisk energi (bananer) för att betala höjningen i systemets potentiella energi (2mgh).
3 För att apan skall "komma igång" måste den utveckla en extra kraft F' för att accelerera (F'=ma). Totala kraften i repet blir då F'+F. Hur kan då det utförda arbetet bli F2h=2mgh? Jo, energin som fordras för att accelerera apan och vikten kompenseras exakt av energin man vinner tillbaka när apan (och vikten) stannar - rörelseenergin blir potentiell energi.
4 Tankeexperimentet är en klassiker som gjorts pupulärt av Lewis Carrol (författaren till Alice i Underlandet). Länk 1 ger ett av många exempel på webben. Länk 2 går till Lewis Carrrols hemsida.
Fundera: vad skulle hända om repet inte är viktlöst? Svaret finns under länk 2.
Hej Daniel och ni andra oense!
Så detta problemet var del av IQ-testen? I så fall klarar jag i varje fall en fråga :-).
Försöksuppställning: se nedanstående bild.
Om trissan är friktionsfri och repet viktlöst, så kan vi först konstatera att apan och vikten har samma massa eftersom dom utövar samma kraft (jämviktsvillkoret). Låt oss anta att denna massa är m. Tyngkraften blir då mg, och denna kompenseras med spänningskraften i repet: F=mg.
För att apan skall kunna klättra måste den utöva en ytterligare kraft uppåt (se nedanstående diskussion). Denna kraft fortplantar sig i repet och kommer även att påverka vikten. Eftersom massan är lika, så kommer vikten att exakt spegla apans rörelser. Så om apan klättrar höjden h, så kommer vikten att höjas lika mycket.
Låt oss diskutera några aspekter på tankeexperimentet.
1 Eftersom vikten sitter fast i repet kommer detta att förskjutas med beloppet h. Apan måste alltså klättra sträckan 2h i förhållande till repet.
2 Man kanske skulle kunna luras av att tillämpa energiprincipen och säga att om apan klättrar höjden h så kompenseras detta med att vikten sjunker med samma belopp. Detta är naturligtvis fel, eftersom det är inget som säger att den potentiella energin i systemet skall bevaras. Apan tar av sitt förråd av kemisk energi (bananer) för att betala höjningen i systemets potentiella energi (2mgh).
3 För att apan skall "komma igång" måste den utveckla en extra kraft F' för att accelerera (F'=ma). Totala kraften i repet blir då F'+F. Hur kan då det utförda arbetet bli F2h=2mgh? Jo, energin som fordras för att accelerera apan och vikten kompenseras exakt av energin man vinner tillbaka när apan (och vikten) stannar - rörelseenergin blir potentiell energi.
4 Tankeexperimentet är en klassiker som gjorts pupulärt av Lewis Carrol (författaren till Alice i Underlandet). Länk 1 ger ett av många exempel på webben. Länk 2 går till Lewis Carrrols hemsida.
Fundera: vad skulle hända om repet inte är viktlöst? Svaret finns under länk 2.

Hur beräknar man perioden för en konisk pendel?
Fråga:
Hur kommer man fram till formeln:
T = 2pSqrt[(cos(a)l)/g]
Hos en cirkulär pendel...
Tack!
/John B, Tengbergsgymnasiet, Broviken 2005-04-07
Hur kommer man fram till formeln:
T = 2pSqrt[(cos(a)l)/g]
Hos en cirkulär pendel...
Tack!
/John B, Tengbergsgymnasiet, Broviken 2005-04-07
Svar:
Du menar nog konisk pendel, se nedanstående figur. Vi har en vikt med massan m upphängd i en tråd med längd l. Vikten sätts i rotation så att tråden sveper ut en kon, därav namnet. För att räkna ut rotationsperioden gäller det bara att balansera krafterna.
Två krafter verkar på vikten: spänningen i tråden t och tyngdkraften mg. Dessa två krafter är inte i balans, utan det återstår en horisontell komponent av t (Fc ) riktad mot rotationscentrum. Detta är centripetalkraften som får vikten att beskriva en cirkelrörelse. Den vertikala komponenten av t skall ta ut tyngdkraften mg. Om omloppshastigheten är v är centripetalkraften
Fc = mv2/r (1)
Perioden T, som vi söker blir
T = (cirkelns omkrets)/hastigheten = 2pr/v (2)
Från jämvikt och geometri får vi:
tcos(a) = mg (3)
tsin(a) = mv2/r (4)
r = lsin(a) (5)
Eliminering av t genom division (4)/(3) ger
tan(b) = v2/r2(r/g) (6)
Insättning av värdet på v/r från (6) i (2) och användning av (5) ger slutligen efter lite förenkling:
T = 2pSqrt[(cos(a)l)/g]
Se ävenpendel, plan .
Du menar nog konisk pendel, se nedanstående figur. Vi har en vikt med massan m upphängd i en tråd med längd l. Vikten sätts i rotation så att tråden sveper ut en kon, därav namnet. För att räkna ut rotationsperioden gäller det bara att balansera krafterna.
Två krafter verkar på vikten: spänningen i tråden t och tyngdkraften mg. Dessa två krafter är inte i balans, utan det återstår en horisontell komponent av t (Fc ) riktad mot rotationscentrum. Detta är centripetalkraften som får vikten att beskriva en cirkelrörelse. Den vertikala komponenten av t skall ta ut tyngdkraften mg. Om omloppshastigheten är v är centripetalkraften
Fc = mv2/r (1)
Perioden T, som vi söker blir
T = (cirkelns omkrets)/hastigheten = 2pr/v (2)
Från jämvikt och geometri får vi:
tcos(a) = mg (3)
tsin(a) = mv2/r (4)
r = lsin(a) (5)
Eliminering av t genom division (4)/(3) ger
tan(b) = v2/r2(r/g) (6)
Insättning av värdet på v/r från (6) i (2) och användning av (5) ger slutligen efter lite förenkling:
T = 2pSqrt[(cos(a)l)/g]
Se även

Plan pendel
Fråga:
Har i och med en laboration kommit i kontakt
med huygens formel för plan pendel
T = 2psqrt[l/g]
Min fråga är hur man kommer fram till denna formel?
Är det just 2p därför att man använder 2pr för att beräkna en cirkels omkrets? Varför är det roten ur l/g?
Jag har letat länge efter en förståelig härledning till denna formel.
/Erik F, Rudbecksskolan, Örebro 2005-05-24
Har i och med en laboration kommit i kontakt
med huygens formel för plan pendel
T = 2psqrt[l/g]
Min fråga är hur man kommer fram till denna formel?
Är det just 2p därför att man använder 2pr för att beräkna en cirkels omkrets? Varför är det roten ur l/g?
Jag har letat länge efter en förståelig härledning till denna formel.
/Erik F, Rudbecksskolan, Örebro 2005-05-24
Svar:
Till skillnad från den koniska pendeln (se fråga [13934]) är hastigheten för den plana pendeln inte konstant utan varierar harmoniskt (sinusfunktion). Detta betyder att man måste lösa en andra ordningens differentialekvation och dessutom approximera sin(vinkel) med vinkeln i radianer. Härledningen finns under länk 1. 2p kommer från förvandling av vinkelfrekvens till period, så det har att göra med cirkelns omkrets eller snarare att ett helt varv 360o är 2p radianer.
Så tyvärr finns det för detta fallet ingen enkel härledning, men låt oss ändå titta lite på härledningen i länk 1 (bilden nedan).
Massan m förekommer både i återställande kraften och i uttrycket för accelerationen. Det betyder att vi kan förkorta bort m. Pendelrörelsen är alltså oberoende av massan (liksom fallrörelsen) men den beror av tyngdaccelerationen g.
L kommer in genom sambandet mellan vinkel och läge
x = qL
Lösningen längst ner i figuren är alltså vad man kallar en harmonisk svängningsrörelse. Om perioden är T får vi
(en period hos sinusfunktionen) = 2p = sqrt(g/L)T
dvs
T = 2psqrt[L/g]
I länk 2 finns en kalkylator som gör beräkningar lättare.
Till skillnad från den koniska pendeln (se fråga [13934]) är hastigheten för den plana pendeln inte konstant utan varierar harmoniskt (sinusfunktion). Detta betyder att man måste lösa en andra ordningens differentialekvation och dessutom approximera sin(vinkel) med vinkeln i radianer. Härledningen finns under länk 1. 2p kommer från förvandling av vinkelfrekvens till period, så det har att göra med cirkelns omkrets eller snarare att ett helt varv 360o är 2p radianer.
Så tyvärr finns det för detta fallet ingen enkel härledning, men låt oss ändå titta lite på härledningen i länk 1 (bilden nedan).
Massan m förekommer både i återställande kraften och i uttrycket för accelerationen. Det betyder att vi kan förkorta bort m. Pendelrörelsen är alltså oberoende av massan (liksom fallrörelsen) men den beror av tyngdaccelerationen g.
L kommer in genom sambandet mellan vinkel och läge
x = qL
Lösningen längst ner i figuren är alltså vad man kallar en harmonisk svängningsrörelse. Om perioden är T får vi
(en period hos sinusfunktionen) = 2p = sqrt(g/L)T
dvs
T = 2psqrt[L/g]
I länk 2 finns en kalkylator som gör beräkningar lättare.

Hur räknar man ut optimal utgångsvinkel vinkel för en golfboll?
Fråga:
Om jag slår en golfboll med en driver kommer den
att lämna peggen i med en viss hastighet och vinkel.
Jag vet att klubbans hastihet är ca 190km/h och boll hastigheten ca 280 km/h utgångsvinkeln är ca 17 grader
Hur räknar man ut optimal (max) höjd för en golfboll?
Vilka parametrar måste man känna till?
/Roland A, Båstad 2005-06-22
Om jag slår en golfboll med en driver kommer den
att lämna peggen i med en viss hastighet och vinkel.
Jag vet att klubbans hastihet är ca 190km/h och boll hastigheten ca 280 km/h utgångsvinkeln är ca 17 grader
Hur räknar man ut optimal (max) höjd för en golfboll?
Vilka parametrar måste man känna till?
/Roland A, Båstad 2005-06-22
Svar:
Problemet är på grund av luftens inverkan mycket mer komplicerat. En golfboll rör sig inte alls i en kastparabel eftersom luften spelar mycket stor roll. För ett mellanjärn är banan sedd från sidan närmast hypotenusan av en rätvinklig triangel.
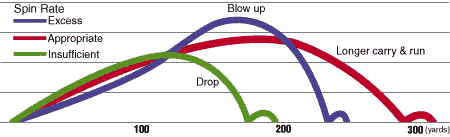
Spinnet och dimplarna (de små groparna) på en golfboll minskar för det första luftmotståndet (genom turbulens) och ger dessutom upphov till en lyftkraft (genom den sk Magnus-effekten). Bilden (från nedanstående länk Flight Dynamics of Golf Balls) visar bollbanan för olika spinn. Det är uppenbart viktigt all få lagom spinn på bollen!
Se Golf Ball Flight Dynamics och nedanstående länkar för olika aspekter på golfbollars rörelse.
och nedanstående länkar för olika aspekter på golfbollars rörelse.
Se ävenkastparabel för rörelse utan hänsyn till luftens inverkan.
Problemet är på grund av luftens inverkan mycket mer komplicerat. En golfboll rör sig inte alls i en kastparabel eftersom luften spelar mycket stor roll. För ett mellanjärn är banan sedd från sidan närmast hypotenusan av en rätvinklig triangel.
Spinnet och dimplarna (de små groparna) på en golfboll minskar för det första luftmotståndet (genom turbulens) och ger dessutom upphov till en lyftkraft (genom den sk Magnus-effekten). Bilden (från nedanstående länk Flight Dynamics of Golf Balls) visar bollbanan för olika spinn. Det är uppenbart viktigt all få lagom spinn på bollen!
Se Golf Ball Flight Dynamics
Se även
Vad är det för skilnad mellan massa och tyngd?
Grundskola_7-9: Kraft-Rörelse [14538]
Fråga:
vad är det för skilnad mellan massa och tyngd? vilka instrument används för att bestämma storlek på massa?
månlandaren lyfte från månen då uppdraget var slutfört då behövde man inte lika stor raketmotor som då man lyfte från jorden varför?
/caroline a, 2006-02-26
vad är det för skilnad mellan massa och tyngd? vilka instrument används för att bestämma storlek på massa?
månlandaren lyfte från månen då uppdraget var slutfört då behövde man inte lika stor raketmotor som då man lyfte från jorden varför?
/caroline a, 2006-02-26
Svar:
Caroline! Låt oss börja med att se vad Nationalencyklopedin säger:
säger:
Massa: den egenskap hos materien som påverkas av gravitationskraften (tung massa) och som motsätter sig rörelseändringar (trög massa).
Tyngd: i en given referensram den kraft som verkar på en kropp och därvid ger den en acceleration lika med den lokala tyngdaccelerationen i denna referensram.
Massa är alltså en universell (överallt gällande) egenskap som är är ett mått på materieinnehåll. Tyngd beror på var massan befinner sig, dvs vilken tyngdkraft den påverkas av. Ett kilogram massa på månen har t.ex. bara tyngden 1/6 kg.
Eftersom massa och tyngd är relaterade använder man normalt en våg för att bestämma båda. Se vidaremassa, trög/tung .
Det behövdes en mycket mindre raketmotor dels för att tyngdkraften på månen är mycket mindre (man behövde uppnå hastigheten 1.3 m/s mot 8 m/s för att komma upp i satellitbana kring jorden). Dels var ju massan hos övre delen av månlandaren mycket mindre än massan hos Saturn V raketen som startade från jorden.
/Peter E 2006-02-26
Caroline! Låt oss börja med att se vad Nationalencyklopedin
Massa: den egenskap hos materien som påverkas av gravitationskraften (tung massa) och som motsätter sig rörelseändringar (trög massa).
Tyngd: i en given referensram den kraft som verkar på en kropp och därvid ger den en acceleration lika med den lokala tyngdaccelerationen i denna referensram.
Massa är alltså en universell (överallt gällande) egenskap som är är ett mått på materieinnehåll. Tyngd beror på var massan befinner sig, dvs vilken tyngdkraft den påverkas av. Ett kilogram massa på månen har t.ex. bara tyngden 1/6 kg.
Eftersom massa och tyngd är relaterade använder man normalt en våg för att bestämma båda. Se vidare
Det behövdes en mycket mindre raketmotor dels för att tyngdkraften på månen är mycket mindre (man behövde uppnå hastigheten 1.3 m/s mot 8 m/s för att komma upp i satellitbana kring jorden). Dels var ju massan hos övre delen av månlandaren mycket mindre än massan hos Saturn V raketen som startade från jorden.
/Peter E 2006-02-26
Vad finns det för bevis för relativitetsteorin?
Fråga:
När kunde man eller kan man fortfarande inte fastställa relativitets teorin? Vilka olika upptäckter och bevis var man tvungna att få fram?
/Frida S, Kullagymnasiet, Höganäs 2006-04-28
När kunde man eller kan man fortfarande inte fastställa relativitets teorin? Vilka olika upptäckter och bevis var man tvungna att få fram?
/Frida S, Kullagymnasiet, Höganäs 2006-04-28
Svar:
Frida! Som fysikaliskt teori måste relativitetsteorin anses mycket etablerad. Detta gäller båderelativitetsteorin, speciella
ochrelativitetsteorin, allmänna . Se
Special_theory_of_relativityConsequences_derived_from_the_Lorentz_transformation och
General_theory_of_relativityConsequences_of_Einstein's_theory
för några experimentella resultat som stöder den speciella och den allmänna relativitetsteorin.
Det universiella navigeringssystemet GPS (seGlobal_Positioning_System och nedanstående figur från Wikimedia Commons) med 24 satelliter i bana runt jorden på en höjd av 20000 km skulle helt enkelt inte fungera om man inte tog hänsyn till relativitetsteorierna.
Dels orsakar banrörelsen att den mycket exakta klockan i en satellit saktar sig 7 mikrosekunder per dygn pga den speciella relativitetsteorin. Eftersom satelliten befinner sig i ett svagare gravitationsfält går klockan 45 mikrosekunder per dygn snabbare. Nettokorrektionen 45-7=38 mikrosekunder per dygn appliceras genom att man justerar klockan att gå lite långsammare innan satelliten skickas upp. Man synkroniserar även alla klockorna med hjälp av klockor på marken. Se vidare länk 1.
Se vidareSpecial_relativity och General_relativity .
Tillägg 5/4/2011:
Uppskattning av effekterna
Konstanter:
Ljushastigheten: c = 3.00108 m/s
Gravitationskonstanten: G = 6.67510-11m3/(kg.s2)
Jordens massa: M = 5.9741024 kg
Jordens radie: R = 6.37106 m
GPS-satelliternas avstånd från jordens centrum (20000 km över jordytan): RGPS = 26.37106 m
Speciell relativitet
Vi räknar från jordens centrum eftersom satelliterna går ganska högt och jordens rotationshastighet är liten (mindre än 500 m/s) jämfört med satelliternas hastighet.
Satellitens hastighet v ges av
mv2/RGPS = mMG/(RGPS)2
vilket blir
v = sqrt(MG/RGPS) = sqrt(5.9710246.6710-11/(26.367106) = 3886 m/s
Klockan påverkas med g-faktorn (Special_relativityTime_dilation_and_length_contraction )
g = sqrt(1-(v/c)2) =
sqrt(1-(3886/300000000)^2) = 0.9999999999161055
Den relativa korrektionen blir
1 - g = 8.38910-11
och korrektionen på ett dygn blir
8.38910-11606024 = 7.2510-6 s
eller c:a 7 mikrosekunder.
Allmän relativitet
Denna korrektion har att göra med att man måste bevara totala energin även i ett gravitationsfält, se fråga [16989], stycket gravitationell rödförskjutning. För att bevara energiprincipen måste tiden i ett starkt gravitationsfält gå långsammare än i ett svagare. Tiden går alltså till synes snabbare i GPS satelliterna än på jordytan. Den relativa korrektionen ges av potentialskillnaden dividerat med viloenergin mc2 (m är satellitens massa som kommer att försvinna i slututtrycket).
Om gravitationspotentialen är U(r) så gäller genom integration av gravitationskraften
U(r) = -mMG/r
Ändringen i potentiell energi om vi går från jordytan till satellitbanan blir
DU = -mMG/RGPS -(-mMG/R) = -mMG(1/RGPS -1/R)
Med insatta värden blir
DU = m4.714 107
Om vi dividerar detta med viloenergin mc2 får vi den relativa korrektionen till
5.237 10-10
På ett dygn blir korrektionen
5.237 10-10246060 s = 45.2 mikrosekunder
vilket stämmer bra med värdet ovan.
Frida! Som fysikaliskt teori måste relativitetsteorin anses mycket etablerad. Detta gäller både
och
för några experimentella resultat som stöder den speciella och den allmänna relativitetsteorin.
Det universiella navigeringssystemet GPS (se
Dels orsakar banrörelsen att den mycket exakta klockan i en satellit saktar sig 7 mikrosekunder per dygn pga den speciella relativitetsteorin. Eftersom satelliten befinner sig i ett svagare gravitationsfält går klockan 45 mikrosekunder per dygn snabbare. Nettokorrektionen 45-7=38 mikrosekunder per dygn appliceras genom att man justerar klockan att gå lite långsammare innan satelliten skickas upp. Man synkroniserar även alla klockorna med hjälp av klockor på marken. Se vidare länk 1.
Se vidare
Tillägg 5/4/2011:
Uppskattning av effekterna
Konstanter:
Ljushastigheten: c = 3.00108 m/s
Gravitationskonstanten: G = 6.67510-11m3/(kg.s2)
Jordens massa: M = 5.9741024 kg
Jordens radie: R = 6.37106 m
GPS-satelliternas avstånd från jordens centrum (20000 km över jordytan): RGPS = 26.37106 m
Speciell relativitet
Vi räknar från jordens centrum eftersom satelliterna går ganska högt och jordens rotationshastighet är liten (mindre än 500 m/s) jämfört med satelliternas hastighet.
Satellitens hastighet v ges av
mv2/RGPS = mMG/(RGPS)2
vilket blir
v = sqrt(MG/RGPS) = sqrt(5.9710246.6710-11/(26.367106) = 3886 m/s
Klockan påverkas med g-faktorn (
g = sqrt(1-(v/c)2) =
sqrt(1-(3886/300000000)^2) = 0.9999999999161055
Den relativa korrektionen blir
1 - g = 8.38910-11
och korrektionen på ett dygn blir
8.38910-11606024 = 7.2510-6 s
eller c:a 7 mikrosekunder.
Allmän relativitet
Denna korrektion har att göra med att man måste bevara totala energin även i ett gravitationsfält, se fråga [16989], stycket gravitationell rödförskjutning. För att bevara energiprincipen måste tiden i ett starkt gravitationsfält gå långsammare än i ett svagare. Tiden går alltså till synes snabbare i GPS satelliterna än på jordytan. Den relativa korrektionen ges av potentialskillnaden dividerat med viloenergin mc2 (m är satellitens massa som kommer att försvinna i slututtrycket).
Om gravitationspotentialen är U(r) så gäller genom integration av gravitationskraften
U(r) = -mMG/r
Ändringen i potentiell energi om vi går från jordytan till satellitbanan blir
DU = -mMG/RGPS -(-mMG/R) = -mMG(1/RGPS -1/R)
Med insatta värden blir
DU = m4.714 107
Om vi dividerar detta med viloenergin mc2 får vi den relativa korrektionen till
5.237 10-10
På ett dygn blir korrektionen
5.237 10-10246060 s = 45.2 mikrosekunder
vilket stämmer bra med värdet ovan.

Rörelseenergi för en rullande kula
Gymnasium: Kraft-Rörelse - golfboll, idrottsfysik, lutande plan, rörelseenergi, tröghetsmoment [14738]
Fråga:
Hejsan! Jag har ett problem.
En kula släpps i en kulbana som står placerad på ett bord, vid kanten. Jag har räknat fram att kulan har fått en viss teoretisk energi när den lämnar banan och den har fått en minde energi i verkligheten.
Jag kan anse att luftmotståndet och friktionen inte har någon påverkan och jag har listat ut att det har något med rotationen av kulan att göra, så min fråga är nu. Vart tar energin vägen på sin resa ned för kulbanan?
svara gärna snabbt, arbetet ska lämnas in denna veckan..
/Anna O, Birger Sjöbergymnasiet, Vänersborg 2006-05-16
Hejsan! Jag har ett problem.
En kula släpps i en kulbana som står placerad på ett bord, vid kanten. Jag har räknat fram att kulan har fått en viss teoretisk energi när den lämnar banan och den har fått en minde energi i verkligheten.
Jag kan anse att luftmotståndet och friktionen inte har någon påverkan och jag har listat ut att det har något med rotationen av kulan att göra, så min fråga är nu. Vart tar energin vägen på sin resa ned för kulbanan?
svara gärna snabbt, arbetet ska lämnas in denna veckan..
/Anna O, Birger Sjöbergymnasiet, Vänersborg 2006-05-16
Svar:
Ditt problem är inte helt lätt, du får nöja dig med en skiss. Lösningen finns under länk 1, men där på engelska.
Vi börjar med att bortse från kulans rotation. Antag kulans massa är m och dess sluthastighet v. Då gäller enligt energiprincipen (potentiell energi på höjden h = kinetisk energi vid botten):
mgh = mv2/2
dvs
v2 = 2gh
Om kulan inte glider alls kommer den att sättas i rotation. Om tyngdpunktens hastighet i detta fallet är u, kommer vinkelhastigheten w att vara u/r där r är kulans radie. (Du får detta resultat eftersom den del av kulan som rör vid kulbanan har hastigheten 0 i förhållande till banan - kom ihåg, inget glid!).
En homogen kulas tröghetsmoment ges av J = 2mr2/5 (TröghetsmomentExempel ) och rotationsenergin är Jw2/2.
) och rotationsenergin är Jw2/2.
Vi adderar translations-kinetiska energin och rotationsenergin och får
mgh = mu2/2 + (2mr2/5)(u/r)2/2 = mu2(1/2) + mu2(1/5)
dvs
u2 = (10/7)gh = 1.43gh
Detta är klart mindre än 2gh som vi fick ovan eftersom ju en del energi går till kulans rotationsenergi. Förhållandet u/v blir ungefär 0.85, alltså 15% lägre hastighet än en kula som glider perfekt och inte roterar.
Förhållandet mellan rotationsenergi och translationsenergi blir enligt ovan
(1/5)/(1/2) = 2:5.
Tillägg om puttning i golf
Golfspelare som puttar bra ser till att slå till bollen med en något uppåtgående rörelse för att bollen om möjligt skall börja rulla omedelbart. Om man slår till bollen helt centralt kommer bollen att glida ett tag på gräset. Friktionen kommer efter ett tag att få bollen att rulla, men rotationsenergin måste tas från rörelseenergin. Bollen bromsas alltså upp för att den skall kunna få rotation. Det visar sig att längden på puttarna blir mycket mer konsistent om man kan få bollen att rulla direkt vid tillslaget.
Tekniken att få överspinn på bollen direkt vid tillslaget används även t.ex. i biljard då man oftast slår till bollen ovanför ekvatorsplanet vilket får bollen att börja rulla omedelbart.
/fa
/Peter E 2006-05-16
Ditt problem är inte helt lätt, du får nöja dig med en skiss. Lösningen finns under länk 1, men där på engelska.
Vi börjar med att bortse från kulans rotation. Antag kulans massa är m och dess sluthastighet v. Då gäller enligt energiprincipen (potentiell energi på höjden h = kinetisk energi vid botten):
mgh = mv2/2
dvs
v2 = 2gh
Om kulan inte glider alls kommer den att sättas i rotation. Om tyngdpunktens hastighet i detta fallet är u, kommer vinkelhastigheten w att vara u/r där r är kulans radie. (Du får detta resultat eftersom den del av kulan som rör vid kulbanan har hastigheten 0 i förhållande till banan - kom ihåg, inget glid!).
En homogen kulas tröghetsmoment ges av J = 2mr2/5 (TröghetsmomentExempel
 ) och rotationsenergin är Jw2/2.
) och rotationsenergin är Jw2/2.Vi adderar translations-kinetiska energin och rotationsenergin och får
mgh = mu2/2 + (2mr2/5)(u/r)2/2 = mu2(1/2) + mu2(1/5)
dvs
u2 = (10/7)gh = 1.43gh
Detta är klart mindre än 2gh som vi fick ovan eftersom ju en del energi går till kulans rotationsenergi. Förhållandet u/v blir ungefär 0.85, alltså 15% lägre hastighet än en kula som glider perfekt och inte roterar.
Förhållandet mellan rotationsenergi och translationsenergi blir enligt ovan
(1/5)/(1/2) = 2:5.
Tillägg om puttning i golf
Golfspelare som puttar bra ser till att slå till bollen med en något uppåtgående rörelse för att bollen om möjligt skall börja rulla omedelbart. Om man slår till bollen helt centralt kommer bollen att glida ett tag på gräset. Friktionen kommer efter ett tag att få bollen att rulla, men rotationsenergin måste tas från rörelseenergin. Bollen bromsas alltså upp för att den skall kunna få rotation. Det visar sig att längden på puttarna blir mycket mer konsistent om man kan få bollen att rulla direkt vid tillslaget.
Tekniken att få överspinn på bollen direkt vid tillslaget används även t.ex. i biljard då man oftast slår till bollen ovanför ekvatorsplanet vilket får bollen att börja rulla omedelbart.
/fa
/Peter E 2006-05-16
** Frågelådan är stängd för nya frågor tills vidare **
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.

Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.

Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar
