Vill du ha ett snabbt svar - sök i databasen
Nyckelord: hastighet
22 träffar
Om två bilar åker ifrånvarandra med hastigeterna 75 km/h. Då avlägsnar ju
dom sig från varandra med 150 km/h
Om två "planeter" åker i från varandra med 60% av ljusets hastighet
då kan do ju inte avlägsna sig från varandra med 120 % av ljusetshastiget.
Hur gör man för att räkna ut det?
/Markus H, Dergården, Lerum 1997-11-09
Man får använda "Einsteins formel för addition av hastigheter" som
bygger på den speciella relativitetsteorin. Om vi kallar
hastigheterna v1 och v2, så blir det relativa hastigheten
(v1+v2)/(1+v1v2/c2).
För
ditt exempel v1=v2=0.6c blir resultatet 1.2c/(1+0.36)=0.88c.
Observera att om en av hastigheterna är c blir den relativa hastigheten
(c+v2)/(1+cv2/c2) = (c+v2)/(1+v2/c) = c(c+v2)/(c+v2) = c
alltså summan blir aldrig högre än c.
/Peter Ekström 1997-11-22
Vad består ljuset av ?
varför har det alltid konstant hastighet oavsett
utgångshastighet?
När uppmättes ljushastigheten första gången?
Av vem? Hur gjorde han?
/Erik �, Lars Kaggskolan, kalmar 1999-08-27
Ljuset är en så kallad elektromagnetisk vågrörelse, men när ljuset
sänds ut och absorberas sker det i bestämda energipaket som kallas
fotoner.
Att ljusets hastighet alltid är konstant (i vakuum) är ett antagande
(så kallat postulat) man gör i den speciella relativitetsteorin.
Det kan därför inte förklaras inom ramen av relativitetsteorin.
Eftersom teorin tycks stämma väl med mätresultat, får vi helt
enkelt konstatera att naturen tycks vara så. Man kan också
undersöka saken med den nyare elektromagnetiska teorin
(kvantelektrodynamiken). Där beror ljusets hastighet på vissa intressanta egenskaper hos vakuum.
I många fall kan det vara svårt att säga vem som var först, men
inte i detta fallet. Det var en dansk astronom som hette Ole Römer.
Året var 1676 och platsen Paris. Han mätte tidpunkterna för
förmörkelser av jupitermånen Io, alltså tidpunkterna då Io
går in i och ut ur Jupiters skugga. Han fann en periodisk variation
med perioden lite mer än ett år. Avståndet till Jupiter varierar ju när
jorden går i sin bana runt solen. Han insåg att den periodiska variationen kunde förklaras om ljuset hade ändlig hastighet, och
han räknade ut ungefär rätt hastighet. Tänk att detta var över
300 år sedan. Ganska genialiskt, eller hur?
Slår man på ljus i Nationalencyklopedin![]() blir man lätt
blir man lätt
förvirrad. I texten beskrivs Ole Römers metod på ett sätt,
och i bildtexten på ett helt annat sätt. I själva verket är
det två oberoende metoder. Han använde sig av båda, och eftersom
de gav samma resultat, kunde han känna sig ganska säker på att han hade rätt.
Mera kan du läsa om det här: The Speed of Light![]() .
.
/KS/lpe 1999-10-15
Hur räknar man ut flykthastigheten hos en kropp?
/Hans B, Anders Ljunstedts Gymnasium, Åmål 1999-10-03
 )
) Flykthastigheten är alltså den minsta hastighet som t.ex. en kanonkula måste haför att lämna jorden. Vi skjuter den rakt upp och bortser frånluftmotståndet. Den kinetiska energin (E) ska vara lika medarbetet (W) som krävs för att lyfta upp kanonkulan ut i rymden.
E = W
E = mv2/2
W = GmM/r
m = kanonkulans massa, v = kanonkulans hastighet, G = gravitationkonstanten,M = jordens massa, r = jordens radie
Uttrycket för W får man fram genom att notera att arbetet är lika medintegralen av kraften med avseende på vägen. Vi integrerar alltsåkraften från jordytan mot oändligheten. Kraften (f) ges av Newtonsgravitationsteori:
f = GmM/r2
Integralen (från r till oändligheten) blir
W = GMm/r
Ur detta får vi fram uttrycket för flykthastigheten (escape velocity) genom att sätta E = W:
v = (2GM/r)1/2
Låt oss beräkna flykthastigheten för jorden och månen. Gravitationskonstanden G är 6.67410-11 (![]() :
:
Jordens massa: 5.97361024 kg
Jordradien: 6.371106 m
Månens massa: 0.073491024 kg
Månradien: 1.737106 kg
Flykthastgheten för jorden blir då
v = (26.67410-115.97361024/6.371106)1/2 = 11187 m/s = 11.2 km/s
och för månen
v = (26.67410-110.073491024/1.737106)1/2 = 2376 m/s = 2.4 km/s
Se vidare
/KS/lpe 1999-10-15
Varför är ljudets hastighet olika i olika material?
Varför är ljudets hastighet olika i olika material. Vad beror det på?
/Rikard S, 1999-12-08
För gaser är det ganska enkelt, ljudhastigheten beror på molekylernas hastighet, som i sin tur beror på temperaturen och molekylvikt, se fråga [12639]. Ljudhastigheten beror alltså inte på t.ex. densiteten som för fasta ämnen och vätskor (se nedan). Anledningen till att gaser och fasta ämnen/vätskor beter sig så olika är att i en gas är molekylerna helt fria - de påverkar inte varandra med krafter som i fasta ämnen/vätskor.
I väte och helium (lätta gaser) är ljudhastigheten 1300 m/s och
900 m/s repektive. Jämför luft, 330 m/s.
I vätskor är det inte så enkelt, där kommer krafterna mellan molekylerna in.
Liksom för gaser ökar ljudhastigheten i de flesta vätskor med temperaturen.
Vatten är ett undantag.
I fasta ämnen är det mera komplicerat, där talar man om två olika
ljudhastigheter, för longitunell våg och för transversell våg.
Longitudinell = svängningsrörelser i färdriktningen.
Transversell = svängningsrörelser vinkelrätt mot färdriktningen.
Den longitudinella vågen tar sig fram ungefär
dubbelt så snabbt som den transversella. Också här spelar bindningarna
mellan atomerna en stor roll. I en hård metall som beryllium är de två
hastigheterna 13000 m/s och 9000 m/s. I en mjuk metall som bly är de
2200 m/s och 700 m/s. Här kommer också in att beryllium är en lätt atom, medan blyatomen är tung.
För vissa fasta och flytande ämnen ges (se länk 1) ljudhastigheten av
v = sqrt(E/r)
där E är elasticitetsmodulen och r är densiteten. Uttrycket stämmer t.ex. mycket bra för vatten. För fasta ämnen tillkommer dessutom komplikationen att ljudhastigheten är olika i olika riktningar.
Hur kan man förstå ovanstående uttryck åtminstone kvantitativt? Föreställ dig en löst spänd gitarrsträng. Den svänger med en låg frekvens f. Eftersom v = fl där l är våglängden (som för grundtonen är 2L där L är strängens längd), så blir utbredningshastigheten låg. Om vi spänner strängen hårdare blir f högre, l är detsamma, så v blir högre. Spänningen i strängen motsvarar elasticitetsmodulen E.
På motsvarande sätt motsvarar densiteten r massan hos stängen. Det vill säga att hög densitet gör svängningen långsammare (tänk på de olika tjocka men lika långa gitarrsrängarna).
För elastiska material med låg densitet (t.ex. järn) är alltså ljudhastigheten hög, medan den för icke elastiska material med hög densitet (bly) är låg. Se länk 2.
Se vidare
/KS/lpe 2000-01-14
Ole Römer räknade ut ljusets hastighet m h a observationer av Jupiters
månar från olika positioner på jorden i banan runt solen.
Detta byggde på att han kände till jordens medelavstånd till solen.
Hur och när bestämdes jordens avstånd till solen?
/Anders L, Sunnerboskolan, Ljungby 2001-02-03
Man hade faktiskt mätt avståndet till solen på den tiden (1670-talet).
Känner man ett avstånd i solsytemet, känner man (genom Keplers
lagar) alla. Man hade mätt avståndet till Mars en gång när Mars
var nära jorden. Den metod man använde var parallaxmetoden, alltså
att Mars står på något olika ställen på himlen, sett från olika platser
på jorden. Det var ingen särskilt noggrann mätning, gissningsvis 20% fel.
Se även: The Speed of Light
/KS 2001-02-03
Jag tror jag har förstått att rösten blir ljusare om man inandas helium
därför att ljudhastigheten i denna gas är högre än i luft. Jag förstår
dock inte hur denna högre hastighet uppstår? Jag jämför gärna med ljudets
högre hastighet i tättare medier som vatten och stål och blir då förvirrad.
Kan Ni reda ut?
/Fredrik H, 2001-04-24
Ljudhastigheten i en gas är proportionell mot molekylernas medelhastighet.
Temperaturen är proportionell mot molekylernas medelenergi. Jämför vi nu en
tung (M) och en lätt (m) gas vid samma temperatur får vi:
mv2/2 = MV2/2
vilket ger
v/V = (M/m)0.5
sätter vi in M =28 (kväve) och m = 4 (helium) får vi
v/V = (28/4)0.5 = 70.5 = 2.65
Ljudhastigheten i helium vid rumstemperatur är alltså
340 2.65 = 900 m/s.
Ljudhastigheten i vätskor och fasta ämnen bestäms av andra faktorer.
/KS 2002-04-29
Bland era frågor/svar finner jag flera intressanta svar på frågor som
berör elektronernas hastighet i en ledare. Jag lär mig att hastigheten
är beroende av ledarens tvärsnittsarea och strömstyrkan. 1)Finns det
formel för att räkna ut denna hastighet? 2)Hur ser ni som är
ämnesföreträdare på resonemang av denna typ: "Ju högre spänning,
desto snabbare rör sig elektronerna vilket i sin tur medför att
exempelvis en lampa som är ansluten till kretsen lyser starkare.
" Traditionellt antar jag att en lärare skulle tala om att högre
spänning ger en större ström i en viss krets, jag är intresserad
av vilka fysikaliska betänkligheter ni kan se om vi istället skulle
tala i termer av elektroners hastighet. Det senare tilltalar elevers
förförståelse i betydligt mycket mer än ex förklaringar som bygger på
analogier (tex vattenanalogin) av olika slag.
/Mattias L, 2002-02-05
En del av elektronerna i en metall är fria, det vill säga att de inte är
bundna till en särskild atom. De bildar en speciell typ av gas (Fermigas).
Antalet fria elektroner per atom kan vara 1 till 6. Det är denna Fermigas
som binder ihop atomerna i metallen. Alkalimetallerna (som natrium och kalium)
har en fri elektron och är löst bundna. De är mjuka och har låg smältpunkt.
Wolfram har 6 fria elektroner och är hårt bunden. Metallen är hård och har
mycket hög smältpunkt.
Det är denna elektrongas som bestämmer de metalliska egenskaperna som
metallglans och ledningsförmåga för elektricitet och värme. Typisk
hastighet för elektronerna i denna gas är 1000 km/s. Alltså, när man
talar om elektronernas "hastighet" i en ledare, menar man i de flesta
fall elektrongasens drifthastighet.
Detta som inledning till dina frågor.
1. Vad du behöver veta är att 1 A = 1 C/s och att elektronladdningen
är 1.6 10-19 C. Dessutom behöver du veta elektrontätheten, ne (fria elektroner/m3.
För att räkna ut denna behöver du veta antalet fria elektroner per
atom (1 - 6), densiteten, atomvikten och Avogadros tal
(6.022 1023 mol-1). Sedan är det bara att räkna på.
2. Det primära är strömmen. Sedan kan man ju använda Ohms lag för att räkna om till spänning.
Ett uttryck för drifthastigheten vd kan härledas från den på tiden t transporterade laddningen
Q = vdtAneq
A är ledningens tvärsnittsyta och q är elektronens laddning 1.6010-19 C. Dividerar man med t får man
Q/t = I = vdAneq
och
vd = I/(Aneq)
Om man sätter in rimliga värden får man det mycket låga värdet c:a 0.28 mm/s, se bilden nedan och

Ljushastigheten tycks ju vara en konstanternas konstant,
men finns det någon bra anledning till att just ljushastigheten blivit
till någonting så absolut?
/Jimmy K, Martin-Kochgymnasiet, Hedemora 2002-03-19
Det här är en fundamental och intressant fråga. Ljushastigheten (c) beror
på de elektriska och magnetiska egenskaperna hos vakuum. Vi har sambandet:
c2 = 1/(eo
mo)
Alltså, ljushastigheten i kvadrat är lika med den inverterade produkten av
dielektricitetskonstanten för vakuum och den magnetiska permeabiliteten för
vakuum. Dessa konstanter har samma värde hur vi än rör oss. Alltså
är ljusets hastighet densamma, hur vi än rör oss. Detta är grunden
för den speciella relativitetsteorin.
I den klassiska mekaniken och i vardagstillvaron kan vi addera hastigheter.
Det kan man inte i relativitetsteorin.
Man kan fråga sig vad det är som ligger bakom dessa egenskaper hos vakuum.
Kvantelektrodynamiken ger en viss belysning av detta. Där beskrivs ljusets
utbredning som att energin producerar ett virtuellt elektron-positron par,
som snabbt förintar sig, och återutsänder ljuset. Det gör att ljuset inte
går oändligt snabbt, utan måste "sega" sig fram genom vakuum med futtiga
299792458 m/s.
Det var många långa ord i det här svaret!
/KS 2003-02-28
Energi från ett svart hål.
Tja, jag läste att när en massiv stjärna dör och övergår till ett svarthål en s.k. supernova så kan energi skickas ut i form av gravitations vågor. ibland kan det röra sig om så mkt som 10^44 joule. Vart kommer denna energi ifrån är den totala massan mindre efter?
/Karl J, Hjärteskolan, Trosa 2005-12-15
Energin kommer från bindningenergin. En massa som faller ner i ett svart hål binds av gravitationsfältet på samma sätt som en elektron binds i en atom. Elektronen skickar ut ljus när den övergår till lägre tillstånd. Det kan även infallande materia i ett svart hål göra genom kollisioner och uppvärmning, men en massa som rör sig snabbt kan även sända ut
Den energi som sänds ut som elektromagnetisk strålning eller gravitationsvågor är förlorad, så massan av det kompakta objektet minskar med detta belopp. Låt oss titta lite närmare på energiförhållandena.
Klassiskt (Newton) är flykthastigheten från en massa M med radien R är lika med ljushastigheten c när
R = RS = 2GM/c2
(flykthastigheten är v = (2GM/r)1/2, se fråga [3782]).
Gravitationell bindningsenergi för en massa m vid ytan (kallas händelsehorisonten eller Schwarzschild-radien) av ett svart hål blir då
GMm/RS = mc2/2
vilket är exakt halva vilomassan mc2. Om man i stället använder den allmänna relativitetsteorin (vilket vi självklart måste göra) blir uttrycket för händelsehorisonten oförändrad men den gravitationella bindningsenergin blir lika med vilomassan mc2.
Hur skall vi tolka detta? Om vi låter en massa m falla ner i ett svart hål kan vi frigöra maximalt energin mc2/2. Resten kommer att försvinna som rödförskjutning. Ett svart hål är alltså en mycket effektiv energikälla - fusion frigör t.ex. bara någon procent av vilomassan. Detta är orsaken till att man tror att de mest energetiska objekten vi känner till, t.ex. kvasarer, är svarta hål. Om energin frigöres när massan är vid händelsehorisonten blir rödskiftet oändligt, och ingen energi slipper ut. Om vi emellertid låter energin stråla ut när massan är på väg ner, så kan en del av energin slippa ut - maximalt mc2/2.
Länk 1 innehåller information från en expert på området. Länk 2 är en användbar formelsamling för svarta hål. Se även
/Peter E 2005-12-16
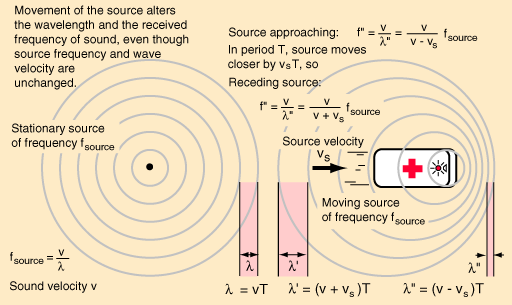
Hur räknar man ut dopplereffekten för ljud?
Ljudets hastighet i luft är 340 m/s. Om man tänker sig att ett objekt som färdas i 340 m/s sänder ut ljudvågor, hur stor blir då frekvensen? Stämmer min teori att frekvensen då blir lika med noll?
/Linnéa A, 2006-11-08
Hej Linnéa! Nej, så enkelt är det inte! Om källan rör sig bort från observatören blir frekvensen hälften av frekvensen hos källan.
 )
)Låt oss titta på hur man får fram detta. Figuren nedan från länk 1 kan vara till hjälp för förståelsen. Beteckningar:
Primade variabler (med ') - observatörens värden
Oprimade variabler - värden hos källan
f - frekvensen
v - ljudhastigheten
vo - observatörens hastighet i förhållande till luften
vs - källans (eng source) hastighet i förhållande till luften
T = 1/f - perioden för svängningen (tiden för en svängning)
l - svängningens våglängd
För alla vågrörelser gäller
lf = l/T = v (hastighet är sträcka dividerat med tid)
Om källan rör sig bort från observatören kommer våglängden att förlängas med ett belopp som är hur långt källan hinner på tiden T:
l' = l + vsT = v/f + vs/f
men l' = v/f ' så vi får om vi inverterar ovanstående ekvation:
f ' = f(v/(v+vs)) (1 rörlig källa, från observatören)
Om källan rör sig mot observatören får vi med samma resonemang:
f ' = f(v/(v-vs)) (2 rörlig källa, mot observatören)
Tillämpar vi (1) på ditt problem får vi
f ' = f(340/(340+340)) = f/2
Som vi ser av (1) så går f ' mot 0 när vs blir mycket stort. Från (2) kan vi se att f ' går mot oändligheten när vs närmar sig ljudhastigheten v.
Vad händer då om observatören rör sig och källan står stilla? I detta fallet är resonemanget lite enklare eftersom våglängden inte ändras. För att från våglängden räkna ut frekvensen måste vi ta hänsyn att den observerade ljudhastigheten blir v+vo om observatören rör sig mot källan. Vi får då
T' = l'/(v+vo) =
(v/f)/(v+vo)
= 1/f '
Om vi inverterar ekvationen får vi
f ' = f(v+vo)/v (3 rörlig observatör, mot källan)
Om observatören rör sig från källan
f ' = f(v-vo)/v (4 rörlig observatör, från källan)
Vi ser från 4 att frekvensen går mot noll när vo går mot v. För vo>v "kör observatören ifrån" ljudet.
Länk 1 innehåller även en praktisk dopplerskiftskalkylator. Se även
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.
Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar

