Svar:
För gaser är det ganska enkelt, ljudhastigheten beror på molekylernas hastighet, som i sin tur beror på temperaturen och molekylvikt, se fråga [12639]. Ljudhastigheten beror alltså inte på t.ex. densiteten som för fasta ämnen och vätskor (se nedan). Anledningen till att gaser och fasta ämnen/vätskor beter sig så olika är att i en gas är molekylerna helt fria - de påverkar inte varandra med krafter som i fasta ämnen/vätskor.

I väte och helium (lätta gaser) är ljudhastigheten 1300 m/s och
900 m/s repektive. Jämför luft, 330 m/s.

I vätskor är det inte så enkelt, där kommer krafterna mellan molekylerna in.
Liksom för gaser ökar ljudhastigheten i de flesta vätskor med temperaturen.
Vatten är ett undantag.

I fasta ämnen är det mera komplicerat, där talar man om två olika
ljudhastigheter, för longitunell våg och för transversell våg.

Longitudinell = svängningsrörelser i färdriktningen.

Transversell = svängningsrörelser vinkelrätt mot färdriktningen.

Den longitudinella vågen tar sig fram ungefär
dubbelt så snabbt som den transversella. Också här spelar bindningarna
mellan atomerna en stor roll. I en hård metall som beryllium är de två
hastigheterna 13000 m/s och 9000 m/s. I en mjuk metall som bly är de
2200 m/s och 700 m/s. Här kommer också in att beryllium är en lätt atom, medan blyatomen är tung.

För vissa fasta och flytande ämnen ges (se länk 1) ljudhastigheten av

v = sqrt(E/r)

där E är elasticitetsmodulen och r är densiteten. Uttrycket stämmer t.ex. mycket bra för vatten. För fasta ämnen tillkommer dessutom komplikationen att ljudhastigheten är olika i olika riktningar.

Hur kan man förstå ovanstående uttryck åtminstone kvantitativt? Föreställ dig en löst spänd gitarrsträng. Den svänger med en låg frekvens f. Eftersom v = fl där l är våglängden (som för grundtonen är 2L där L är strängens längd), så blir utbredningshastigheten låg. Om vi spänner strängen hårdare blir f högre, l är detsamma, så v blir högre. Spänningen i strängen motsvarar elasticitetsmodulen E.

På motsvarande sätt motsvarar densiteten r massan hos stängen. Det vill säga att hög densitet gör svängningen långsammare (tänk på de olika tjocka men lika långa gitarrsrängarna).

För elastiska material med låg densitet (t.ex. järn) är alltså ljudhastigheten hög, medan den för icke elastiska material med hög densitet (bly) är låg. Se länk 2.

Se vidare Sound och Speed_of_sound.
/KS/lpe 2000-01-14

Svar:
Ljudhastigheten i en gas är proportionell mot molekylernas medelhastighet.
Temperaturen är proportionell mot molekylernas medelenergi. Jämför vi nu en
tung (M) och en lätt (m) gas vid samma temperatur får vi:

mv²/2 = MV²/2

vilket ger

v/V = (M/m)^0.5

sätter vi in M =28 (kväve) och m = 4 (helium) får vi

v/V = (28/4)^0.5 = 7^0.5 = 2.65

Ljudhastigheten i helium vid rumstemperatur är alltså
340 2.65 = 900 m/s.

Ljudhastigheten i vätskor och fasta ämnen bestäms av andra faktorer.
/KS 2002-04-29

Svar:
Hej Linnéa! Nej, så enkelt är det inte! Om källan rör sig bort från observatören blir frekvensen hälften av frekvensen hos källan.

Dopplereffekt är ett fysikaliskt fenomen, som innebär en förändring av frekvensen (svängningstalet) hos en signal, till exempel ljud eller ljus, beroende på om källan närmar sig eller avlägsnar sig i förhållande till observatören. Först med att beskriva dopplereffekten var Christian Doppler 1842. Det allra lättast iakttagbara exemplet på dopplereffekten är ljudsirenerna på ambulanser eller polisbilar, som tycks minska i frekvens då de passerar observatören. (Dopplereffekt)

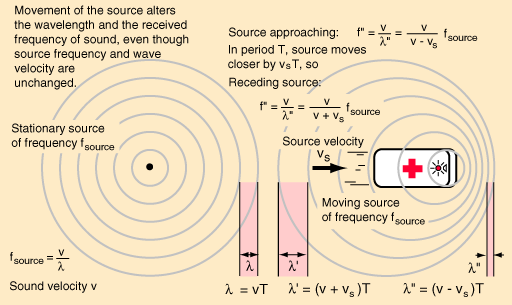
Låt oss titta på hur man får fram detta. Figuren nedan från länk 1 kan vara till hjälp för förståelsen. Beteckningar:

Primade variabler (med ') - observatörens värden

Oprimade variabler - värden hos källan

f - frekvensen

v - ljudhastigheten

v_o - observatörens hastighet i förhållande till luften

v_s - källans (eng source) hastighet i förhållande till luften

T = 1/f - perioden för svängningen (tiden för en svängning)

l - svängningens våglängd

För alla vågrörelser gäller

lf = l/T = v (hastighet är sträcka dividerat med tid)

Om källan rör sig bort från observatören kommer våglängden att förlängas med ett belopp som är hur långt källan hinner på tiden T:

l' = l + v_sT = v/f + v_s/f

men l' = v/f ' så vi får om vi inverterar ovanstående ekvation:

f ' = f(v/(v+v_s)) (1 rörlig källa, från observatören)

Om källan rör sig mot observatören får vi med samma resonemang:

f ' = f(v/(v-v_s)) (2 rörlig källa, mot observatören)

Tillämpar vi (1) på ditt problem får vi

f ' = f(340/(340+340)) = f/2

Som vi ser av (1) så går f ' mot 0 när v_s blir mycket stort. Från (2) kan vi se att f ' går mot oändligheten när v_s närmar sig ljudhastigheten v.

Vad händer då om observatören rör sig och källan står stilla? I detta fallet är resonemanget lite enklare eftersom våglängden inte ändras. För att från våglängden räkna ut frekvensen måste vi ta hänsyn att den observerade ljudhastigheten blir v+v_o om observatören rör sig mot källan. Vi får då

T' = l'/(v+v_o) =
(v/f)/(v+v_o)
= 1/f '

Om vi inverterar ekvationen får vi

f ' = f(v+v_o)/v (3 rörlig observatör, mot källan)

Om observatören rör sig från källan

f ' = f(v-v_o)/v (4 rörlig observatör, från källan)

Vi ser från 4 att frekvensen går mot noll när v_o går mot v. För v_o>v "kör observatören ifrån" ljudet.

Länk 1 innehåller även en praktisk dopplerskiftskalkylator. Se även Doppler_effect.

/Peter E 2006-11-08

Svar:
Hej Marie! Intressant fråga! Jag har inte observerat effekten själv, men jag tror det finns två samverkande effekter.

1 Ditt eget förslag: varm luft har lägre densitet så den stiger. Vi har alltså en luftström uppåt. När ljudvågorna kommer in i den uppåtgående luftströmmen kommer ljudet att böjas av lite uppåt eftersom ljudvågorna följer med luftstömmen. Ljudvågor som går nära marken (som kunde tänkas böjas upp för att träffa ett öra på andra sidan elden) stoppas av materialet som bygger upp elden.

2 Ljudhastigheten beror av temperaturen hos luften, se fråga 12639. Den är proportinell mot roten ur luftens absoluta temperatur (temperatur i Kelvin, T). Om luftens temperatur är 20+273=c:a 300 K och eldens temperatur är 600+273 = c:a 900 K, blir ljudhastigheten i elden ungefär sqrt(3)=1.7 gånger högre än i luften. En ljudvågfront som går in i elden kommer då att vrida sig utåt - elden fungerar som en negativ (spridande) lins för ljus. Ljudfronten sprids alltså ut över ett större område, vilket innebär att intensiteten minskar. En besläktad effekt beskrivs i Sound_speed_gradient.

Jag vet inte vilken av effekterna som dominerar, men de bör båda kunna bidra till en försvagning av ljudet på andra sidan elden.

Luften ovanför elden är också mycket turbulent, vilket medför att ljudvågorna blir deformerade. Detta stör ytterligare hur man uppfattar ljudet.
/Peter E 2007-09-17

Svar:
Anders! Det låter som en riktigt dålig idé! Visserligen är svavelhexafluoriden inte giftig, men det är en mycket tung gas, och det är risk att så mycket stannar kvar i lungorna att man kan få skador och t.o.m. kvävas!

Principen bakom det faktum att man får mörkare röst är densamma, fast tvärtom, som när man andas in helium och får en ljusare röst (Kalle Anka röst), se fråga [10178]. Helium är mindre farligt eftersom det är lättare än luft. Normalt (om du inte står på huvudet) strävar alltså heliumet att komma ut ur lungorna.

Tillägg 19/11/08:

Nedan finns en kul demonstration av hur tungt svavelhexafluorid är. Enda invändningen mot det första experimentet är att svavelhexafluorid är en oerhört potent växthusgas, så att släppa ut en massa SF₆ är inte bra för miljön! På slutet andas man in SF₆, och det är klart att det tag lång tid för gasen att försvinna! Farligt alltså!

Tack Marcus Erhagen för länktipset!


/Peter E 2008-11-15

Svar:
Sara! Det finns enkla metoder och det finns mer avancerade som ger bättre resultat.

Enklast är att använda samma metod som när man tajmar Usain_Bolt: Starta ett tidtagarur, låt honom springa en uppmätt sträcka och stoppa klockan. Sträckan/tiden är då hastigheten.

Allt du behöver är en vän, ett tidtagarur och en planka. Skicka iväg din vän med plankan åtminstone 300 m bort. Din vän slår plankan i en sten. När du ser plankan träffa stenen startar du uret. När du hör ljudet stoppar du uret. Läs av och skriv ner tiden. Upprepa försöket 10 gånger och beräkna medelvärdet. Mät upp avståndet från dig till din vän så noggrant som möjligt. Om du är hyggligt bra på att använda tidtagaruret bör du kunna få ett värde inom 10% dvs 340+/-40 m/s.

Om man vill ha bättre resultat får man använda lite utrustning. Ställ upp två mikrofoner på någon meters avstånd från varandra. Mät noggrannt upp avståndet mellan mikrofonerna. Ställ dig i förlängningen av linjen mellan mikrofonerna och stick hål på en ballong. Mät avståndet i tid mellan pulserna i mikrofonerna, t.ex. med ett kalibrerat oscilloskop. Ljudhastigheten är då sträckan/tiden. Se länk 1 för mer detaljerade instruktioner.

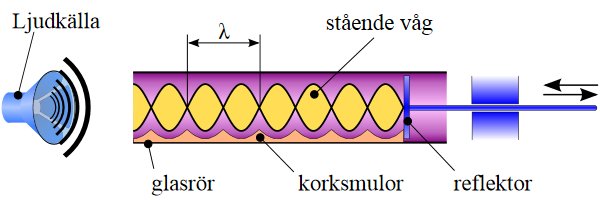
Ett bra sätt är att med hjälp av Kundts rör mäta våglängden, se länk 2 för en detaljerad beskrivning. Svenska Wikipedia (Kundts_rör) beskriver det så här:

Kundts rör är en anordning för att studera ljudvågor uppfunnen vid mitten av 1860-talet av den tyske fysikern August Kundt (1829 — 1894). Anordningen (se nedanstående figur) består av ett genomskinligt horisontellt placerat glasrör, ett par meter långt och några centimeter i diameter. Rörets ena ände är tilltäppt, och framför den andra änden placeras en ljudkälla med konstant frekvens, numera en högtalare, men på Kundts tid användes musikinstrument. I röret har små lätta partiklar av något slag spritts ut längs bottnen, till exempel korksmulor eller frön av något slag. Vid de frekvenser då en stående våg bildas kommer partiklarna att samlas i trycknoderna. Därmed kan ljudets våglängd mätas. Mellan två närliggande noder är det en halv våglängd.

Om man skapar ljudet med en kalibrerad tongenerator kan man även bestämma frekvensen. Sedan beräknar man ljudhastigheten från

ljudhastigheten = frekvensenvåglängden

Ett par enkla metoder beskrivs i Enkla experiment - ljudets hastighet.

Se vidare Speed_of_soundExperimental_methods och Kundt's_tube.

/Peter E 2009-10-06

Svar:
Kajsa! Man lokaliserar ljud genom att man uppfattar tidsskillnaden eller amplitudskillnaden (ljudnivån) mellan signalen till vänster och höger öra. Maximala vägskillnaden för ljud rakt från sidan är för en människa ungefär 0.15 m, ljudhastigheten i luft är 340 m/s, vilket ger en tidsskillnad på 0.15/340 = 0.44 millisekunder. Det är alltså mycket små tidsskillnader man skall kunna detektera för att få riktningsinformation. Bra riktningsinformation kräver god hörsel på båda öronen.

I vatten har man inte alls lika bra riktningskänslighet av två skäl:

1 Som framgår av fråga [13879] är ljudhastigheten i 25-gradigt vatten c:a 1500 m/s vilket är nära 5 gånger högre än hastigheten i luft. Tidskillnaden mellan öronen blir då 5 gånger mindre, vilket påverkar precisionen.

2 Ljudsignalen i vatten går inte som i luft huvudsakligen in i ytterörat och vidare in i innerörat, utan genom att ben i huvudet sätts i vibration. Man har således en mycket mer utspridd källa, vilket ger sämre precision.

Referenser: Hearing_(sense) och Sound_localization, den senare mycket bra men på en ganska avancerad nivå.
/Peter E 2009-11-30

Svar:
Ljud är mekaniska vågor där ett oscillerande tryck överförs genom ett fast material, vätska eller gas. För att klassas som ljud måste frekvenserna vara inom intervallet för hörsel med en nivå som är tillräckligt stark för att höras, se Ljud.

Ljud är alltså tryckskillnader som fortplantar sig genom ett medium med ljudhastigheten.

I gaser och vätskor är ljud en longitudinell (tryckändring i utbredningsriktningen, se nedanstående figur) variation i tryck som rör sig med en hastighet som är oberoende av frekvens och amplitud. Detta är avgörande för att vi skall kunna uppfatta ljud med källor på olika avstånd på samma sätt förutom att styrkan minskar med ökande avstånd.

För ljudhastigheten i olika material:

Gas: [8346] [12639]

Vatten: [19342]

Diverse fasta/flytande medier: [4311]

Se även Sound.

/Peter E 2014-11-27

Svar:

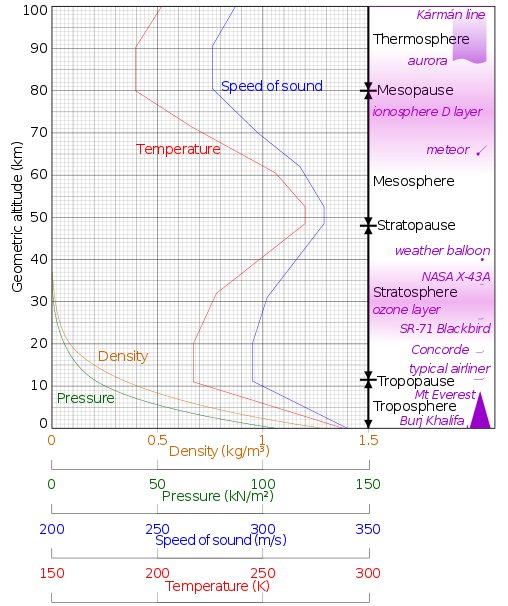
Ljudhastigheten i en ideal gas beror inte av trycket utan endast på absoluta temperaturen och molekylvikten, se fråga [12639]. Eftersom temperaturen i atmosfären varierar med höjden så kommer ljudhastigheten att variera. Temperaturen och ljudhastigheten som funktion av höjden framgår av nedanstående figur från Atmospheric_temperatureTemperature_versus_height. Se även Speed_of_soundDependence_on_the_properties_of_the_medium, Atmosphere_of_EarthTemperature_and_speed_of_sound och länk 2.

/Peter E 2026-02-03