Svar:
Hej Johan!

Nej, jag kan inte förklara problemet. Men jag tror inte heller att olika material skruvar åt olika håll. Tänk t.ex. på en golfboll och en pingisboll. Båda påverkas på samma sätt av underskruv - de påverkas av en kraft uppåt. Detta trots att de har helt olika ytor: golfbollen är knottrig vilket ger turbulent strömning och pingisbollen är slät vilket ger laminär strömning kring bollen. Dessutom finns det ju fotbollar både av plast och av läder, och jag tror en spelare skulle bli mycket förvånad om en ny boll skruvade åt fel håll :-).

Skruv och lyft hos roterande bollar förklaras av den s.k. Magnuseffekten som bygger på Bernoullis ekvation - högre hastighet hos luften ger lägre tryck (Bernoulli's_principle). Se även Magnus_effect.

En helt annan effekt är skruvade kast i kricket, men där har man en asymmetri hos bollen och skruven är riktad i samma riktning som asymmetrin - en underskruvad kricketboll avviker i sidled i stället för i höjdled. Se Swing_bowling.

Se skruvad boll, golfboll och en artikel om fotbollsfysik under länk 1.

Tillägg januari 2017

Magnuseffekten är ett fysikaliskt fenomen som uppträder för roterande kroppar. Effekten innebär att en kropp som rör sig genom en fluid (en vätska eller en gas) samtidigt som den roterar accelereras vinkelrätt mot rörelseriktningen, det vill säga att rörelseriktningen "böjs av". Det är den fysikaliska kraft som gör att roterande bollar får så kallad skruv inom olika bollsporter, se Magnuseffekten och fråga [754].

Video som visar och förklarar Magnuseffekten:



Jag kan inte, trots omfattande sökningar, hitta något väldokumenterat exempel på att materialet i bollen skulle ha någon betydelse. Strukturen på ytan påverkar storleken på Magnus-kraften (dimplarna på en golfboll ökar t.ex. effekten betydligt), men att ett alternativt material skulle ändra kraftens riktning låter inte sannolikt.

Enligt beskrivningen ovan är det plastbollen som uppför sig som väntat. En höger utsida roterar bollen medurs, vilket ger en avvikelse åt höger (den av golfaren fruktade slicen). Kan det vara så att en läderboll är lite asymmetrisk pga en söm (se cricketbollen ovan)? Problemet med denna förklaring är att skruven skulle bero på hur bollen placeras på marken.
/Peter E 2006-08-17

Svar:
Enligt Arkimedes princip är lyftkraften lika med den undanträngda luftens vikt:

lyftkraft = volym(luftens densitet)g

Varmluften i ballongen ger en nedåtriktad kraft, så nettolyftkraften blir

nettolyftkraft = volym(luftens densitet - varmluftens densitet)g

Eftersom det råder jämvikt blir totala massan

M = volym(luftens densitet - varmluftens densitet) = 50010^-6 (1.20 - 0.75) = 0.000225 kg = 0.225 g

Det var ju inte mycket till ballong! Låt oss se vad lyftkraften blir för en rund ballong med radien 5m. Volymen blir

V = 4pr³/3 = 4p5³/3 = 524 m³

Denna ballong kan alltså lyfta massan

M = 524(1.20-0.75) = 236 kg, dvs två personer, korgen och ballongen själv.

Se fråga [7692] om hur man räknar ut luftens densitet vid olika temperaturer.
/Peter E 2006-09-19

Svar:
Marianne! Att räkna med friktion är ganska besvärligt eftersom det är svårt att veta vad friktionskoefficienten är. Det väsentliga i ditt problem är väl ändå doseringen, dvs vägens lutning i en kurva. Låt oss först definiera några storheter.

bilens massa = m

tyngdaccelerationen = g

normalkraften = N

doseringsvinkel = a

bilens hastighet = v

kurvradie = r

Bilen påverkas av två krafter: normalkraften N från vägbanan och mg från tyngdkraften. Om vi sätter samman dessa får vi en resulterande horisontell kraft R mot vägens krökningscentrum. Det är denna kraft som ger den acceleration som får bilen att röra sig med en cirkelbana. Accelerationen är

mv²/r = R = mgtana

Vi får alltså sambandet

v² = rgtana

För en viss given hastighet och kurvradie kan vi alltså med detta uttryck beräkna den optimala doseringsvinkeln. Bilen kan naturligtvis även ta kurvan med en annan hastighet, men då behöver vi friktion för att hålla den kvar på vägen. Om hastigheten är större än v får du mycket riktigt en vertikal komposant. Detta gör att normalkraften ökar, dvs bilen "trycks" mot vägbanan.

Vi har, eftersom vi betraktar bilen från vägens perspektiv, inte infört någon centrifugalkraft, utan vi har en resulterande kraft R som ger en centripetalacceleration.

/Peter E 2006-09-21

Svar:
Hej Joakim! Intressant fråga till en entusiastisk golfare men dålig puttare!

Puttning är egentligen mycket enkelt: slå bollen med rätt hastighet i rätt riktning med hänsyntagande till fall på grund av greenens lutning och eventuell vind. Förutom en god teknik (som finslipas med mycket träning) är självförtroende A och O i golf: alla golfare vet att man misslyckas med de flesta slagen med en klubba man inte "tycker om".

Du har helt rätt i att det är mycket viktigt att få bollen att rulla - inte glida - så snart som möjligt. Detta gör man genom att sätta "överskruv" på bollen, dvs så att bollen roterar i samma riktning som den gör när den rullar. Detta är tvärtom mot skruven som åstadkoms med andra klubbor: klubbladets loft (lutningen mot horisontalplanet) orsakar underskruv, vilket en skicklig spelare kan utnyttja till sin fördel, se golfboll. Du vill alltså ha mycket lite loft på en putter (slagytan skall vara nästan 90 grader mot horisontalplanet), annars får du en i de flesta fall icke önskad underskruv.

Överskruven åstadkommes genom att man täffar bollen när puttern är lite "på uppgång" - bollen lite till vänster i stansen och en pendelrörelse hos klubbhuvudet som når sin lägsta punkt lite innan det träffar bollen. Det fordras lite träning för att lyckas med det varje gång.

Vilka egenskaper bör en bra putter ha?

• Det bör vara lätt att sikta
  
• Tydlig "sweetspot", vilket är den träffpunkt som inte orsakar rotation hos klubbhuvudet
  
• Lite loft (högst några få grader) så man kan åstadkomma överskruv
  
• Ett handtag som ger en känsla för vart klubbhuvudet pekar (ej cylindersymmetriskt)
  

Kan man med elementär fysik förstå varför man vill ha överskruv? Ja, jag tror det. Om man träffar bollen exakt på bakkanten med klubbhuvudet vinkelrätt mot och rörelseriktningen parallellt med den önskade riktningen (square hit), så kommer bollen att glida på underlaget till att börja med. Friktionen mot underlaget får bollen att börja rulla efter ett tag (c:a en meter). Från början har bollen endast rörelseenergi, men när den börjar rulla övergår rörelseenergin delvis i rotationsenergi, se fråga [14738]. Bollen saktar alltså in mycket i början av rörelsen. Pröva att slå några 10-metersputtar med samma svinghastighet dels genom att träffa bollen "square" och dels med överskruv. Du kommer att finna att puttarna med överskruv går betydligt längre än puttarna utan skruv. Dessutom blir längden mycket mer konsistent, och det är detta som gör att tekniken är att föredra. Titta på en god puttare (proffs), så skall du se att bollen rullar mycket snart efter träffen, medan bollen vid en dålig träff glider och hoppar vilket ger ett sämre resultat.

Friktionen (och därmed uppbromsningen) är större när bollen glider (och kanske hoppar) än om den rullar fint. Du får därför en mer konsistent putt med en rullande boll.

Kan man inte få överskruv med ett negativt loft på puttern? Nej, det fungerar antagligen inte eftersom man tvingar bollen nedåt in i greenen. Men kanske skulle man kunna pröva lite negativt loft? Såvitt jag vet finns inga sådana putters, och om det fungerade skulle det säkert finnas det.

En sak är i varje fall säker: om du kan konstruera en putter som gör puttningen lättare och dessutom övertyga golfare att den fungerar, så är du miljonär!

PS. Heter du verkligen Green? Då får du kalla puttern Green-putter!

PS2. Lycka till med puttertillverkningen!

Tillägg juni 2017:

Här är en putter med en speciell yta ("microhinges") som påstås ge bollen överskruv:





Se länk 1 för mer om puttning.
/Peter E 2006-10-14

Svar:
Beatrice! Eftersom en golfboll och en pingisboll är ganska exakt lika stora och har samma form, så är det ganska lätt att förklara. Om vi antar att att utgångshastigheten är lika, så är kraften som orsakas av luftmotståndet lika. En lätt boll (pingisboll) påverkas mer av denna kraft än en tyngre boll (golfboll), vilket innebär att den lättare bollen bromsas snabbare än den tyngre.

För den som vill ha formler gäller att

F = ma

och alltså om kraften F är konstant minskar accelerationen (uppbromsningen) när massan ökar.

Luftmotståndet är för för höga hastigheter proportionellt mot hastigheten i kvadrat (v²) och för lägre hastigheter proportionellt mot hastigheten (v). Länk 1 är en avancerad artikel på engelska.
/Peter E 2006-10-20

Svar:
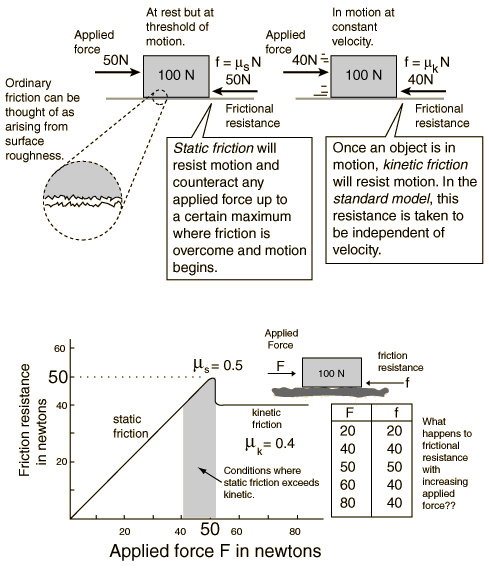
Marianne! Friktionskraften är ett mycket komplicerat fenomen när man djupdyker i det, men standardmodellen är mycket enkel: friktionskraften f är proportionell mot normalkraften N:

f = mN

där proportionalitetskonstanten m kallas friktionskoefficient. Som du ser är det inget beroende av arean. Att det är så kan man intuitivt förstå eftersom om vi t.ex. dubblar arean så blir normalkraften per ytenhet hälften så stor, så resultatet blir oförändrat. Proportionaliteten mellan friktionskraften och normalkraften kan man förstå om man tänker på att den reella kontaktytan (utgörs av några atomer som sticker ut) är ganska liten. Om man ökar normalkraften så kommer atomerna att flytta sig lite, och fler atomer kommer i kontakt med varandra. Detta gör att friktionen ökar. Att den ökar linjärt kan enklast betraktas som ett experimentellt faktum.

Bilderna nedan (från Hyperphysics, länk 1) visar vilofriktion (statisk) och glidfriktion (kinetisk). Den förra är som du säger större. Anledningen är komplex och beror av materialet, men det har att göra med att knöligheter fastnar i varandra när klossen ligger still, medan denna effekt minskar om klossen rör sig.

I den nedre figuren visas friktionskraften f som funktion av den drivande kraften F. Klossen väger 10 kg, så normalkraften är hela tiden c:a 100 N. Till vänster (i origo) är friktionskoefficienten noll (ingen drivande kraft att motverka). Friktionskoefficienten ökar när man går åt höger tills den blir 0.5. Då övervinns friktionskraften och klossen börjar röra sig. Observera att så snart klossen sätts i rörelse så minskar friktionskoefficienten till (i det här exemplet) 0.4.

Se vidare länk 1 och friction för mer om friktion än du någonsin vill veta :-).

/Peter E 2006-10-31

Svar:
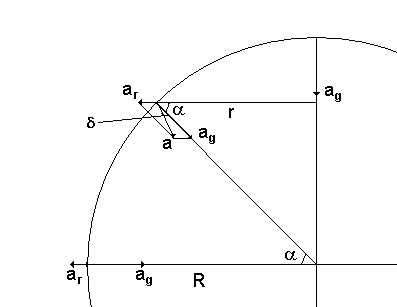
Jon! Det är en helt omärkbar effekt och det är knappast någon risk att man trillar, men låt oss som en övning räkna ut hur stor effekten är. Vi antar att jorden är klotformad och homogen med radien R. Den enda effekt vi tar hänsyn till är jordens rotation, vi bortser alltså från tillplattningen. Vi inför några beteckningar (se figuren):

a_g = 9.822 m/s² tyngdaccelerationen från jordens dragningskraft, se länk 1

a_r accelerationen pga jordens rotation

a den resulterande tyngdaccelerationen

R = 6.3710⁶ m jordradien

a latituden

w = 2p/(246060) = 72.710^-6 s^-1 vinkelhastigheten för jordens rotation

Vid polerna och ekvatorn är det ingen avvikelse i vinkel mellan a och a_g (precis som du säger) medan det för medelhöga latituder är en avvikelse så att det är en liten "uppförsbacke" när man går norrut. Om du så vill kan du förstå detta som att "centrifugalkraften" försöker hindra dig att gå närmare rotationsaxeln.

Låt oss börja med att se vad som händer vid ekvatorn. Rotationshastigheten ges av

v = Rw = 6.3710⁶72.710^-6 = 463 m/s

Accelerationen pga rotationen blir

a_r = v²/R = Rw² = 6.3710⁶(72.710^-6)² = 0.0337 m/s²

Tyngdaccelerationen vid ekvatorn blir alltså

a_g - a_r = 9.822 - 0.0337 = 9.788 m/s²

Accelerationen pga rotationen vid latituden a blir

a_g = rw² = Rcosaw²

Tillämpning av cosinuseoremet på triangeln a_g, a_r, a ger

a² = a_g² + a_r² -2a_ga_rcos(a)

Den andra termen i högra ledet är mycket liten så vi kan försumma den. Vi får då

a = a_g(1 - 2Rw²cos²a/a_g)^1/2 = a_g(1 - Rw²cos²a/a_g) =
a_g(1 - 0.0337cos²a/9.822)

a = a_g(1 - 0.00343cos²a)

Lodlinjens avvikelse från riktningen mot jordens medelpunkt d kan beräknas genom att vi tillämpar sinusteoremet på triangeln:

sind/a_r = sina/a

sind = a_rsina/a =
Rw²cosasina/a =
Rw²sin2a/2a

Från detta uttryck kan vi se att avvikelsen är maximal för a=45^o och noll för a=0^o och a=90^o.

Eftersom a är approximativt lika med a_g och eftersom vinkeln är liten (sind = d) får vi

d = Rw²sin2a/2a_g =
0.0337sin2a/(29.822) =
0.00172sin2a

d i grader blir

d = 1800.00172sin2a/p =
0.0985sin2a grader

Från detta kan vi se att lodlinjens maximala avvikelse (vid latituden 45^o) är c:a 0.1^o.

/Peter E 2006-11-04

Svar:
Andereas! Mycket intressant observation! Vi har testat experimentet och resultatet är exakt som du beskriver det.

Jag tror vi har att göra med samma fenomen som för snurran Tippe-Topp på bilden längst ner, övre raden. Om man sätter snurr på den med handtaget uppåt (som på vänstra bilden), kommer den efter ett tag börja precessera (rotationsaxeln roterar kring en normal till bordsytan) med större och större amplitud för att till sist ställa sig på skaftet (som på högra bilden).

Här är en animerad version av Tippe-Topp (uppdatera sidan för att starta om):



Bilderna nederst visar en snurra som är mycket lik din myntsnurra. Den uppför sig på samma sätt: den extra tyngden förflyttar sig efter en stund upp till toppen av snurran.

Förklaringen är ganska komplicerad, och jag kan här bara antyda vad orsaken är.

En "normal" snurra har en spetsig botten medan denna snurra har en rund. En klassisk snurra kan också börja precessera (se länk 2 för en detaljerad diskussion om precession), med den vänder aldrig helt. För en ideal (utan friktion) snurra måste rörelsemängdsmomentet och rotationsenergin bevaras.

För vår vändande snurra (och Andereas mynt) är det uppenbart att tyngdpunkten ligger högre i det senare läget än i startläget. Snurrans potentiella energi har alltså ökat. Energin för detta tas från rotationsenergin - snurran roterar långsammare i det omvända läget.

Men hur var det nu, skulle vi inte bevara rörelsemängden? Nej, det behöver vi inte om vi har friktion - bevaringslagen gäller bara ett isolerat system. Det är friktionen mellan snurrans botten och bordsytan som dels bromsar upp rotationen men också orsakar en kraft som orsakar ett vridmoment
(friktionskraftens angreppsriktning går inte genom snurrans tyngdpunkt) som får snurran att vrida sig så att den till slut tippar över.

Hans-Uno Bengtsson beskriver fenomenet i detalj och matematiskt i sin bok Fysik för akrobater.
Se även gyroskop för mer om snurrande objekt och fråga [165] om Tippe-Toppen.

/Peter E 2007-01-09

Svar:
Olivia! Nationalencyklopedin säger: kraft, intuitivt ett välbekant vardagsbegrepp, men bakom sinnesförnimmelserna en svårfångad abstraktion.

Wikipedias definition är lite mer konkret (se Kraft): kraftbegreppet är en abstraktion inom fysiken för att förklara och beskriva orsaken till förändringar i ett systems rörelse.

Den grundläggande definitionen är att kraft är alla företeelser som ändrar en kropps rörelsemängd p = m·v:

F = dp/dt = d(mv)/dt = m·dv/dt = m·a

Det finns många olika sorters krafter. De fundamentala kraftverkningarna är gravitationskraft, den svaga kraften, elektromagnetisk kraft och färgkraften.

Sedan finns andra yttringar av kraft, t.ex. rekylkraft, friktionskraft och elastisk kraft. Se vidare Force.
/Peter E 2007-02-05

Svar:
Hej Anna! Ställ en våg under klassrummet. Stäng dörrar och fönster och pumpa ut all luften. Du kommer att se en ändring i utslag som motsvarar luftens vikt :-).

Nej, så enkelt är det inte. Det är inte alls lätt att direkt mäta luftens densitet. Att luften väger något är lättare att visa, se fråga 14454 och länkarna nedan.

Låt oss i stället försöka räkna ut densiteten från andra storheter som är lättare att mäta. Det är ofta så i fysik att något kan vara svårt att mäta direkt medan det kan vara lätt att beräkna med kända fysikaliska lagar och andra storheter.

Vi använder den allmänna gaslagen:

pV = nRT

p = trycket, V = volymen, n = antal moler, R = allmänna gaskonstanten,

T = absoluta temperaturen

Om m är massan gas och M gasens molekylvikt kan vi skriva gaslagen

pV = (m/M)RT

Eftersom densiteten r = m/V får vi

r = pM/(RT)

Normaltrycket är 1.01310⁵ Pa (N/m²), luftens molekylvikt (en blandning av 80% N₂ och 20% O₂) är 28.8. Normal temperatur är 20^oC = 293 K.

Gaskonstanten är 8315 J kmol^-1 K^-1. Vi får då

r = 1.01310⁵28.8/(8315293) = 1.20 kg/m³. Om klassrummet är 10103 = 300 m³, väger luften 3001.20 = 360 kg, alltså lika mycket som fyra manliga normallärare!
/Peter E 2007-02-28