Svar:
Hej Petri! Jag håller i stort med om kunskapsmålen och tycker det låter som att du uppfattat dem mycket bra.

För det första är jag allergisk mot begreppet förklara när det gäller fysikens lagar. Förklara är för mig svar på frågan varför?. I djupare mening vet vi inte varför naturlagarna är som de är, se fråga [12126].

Fysik är en empirisk vetenskap som i grunden bygger på observationer och experiment, se fråga [14232]. Fysiken använder matematik som ett verktyg, men fysik är inte matematik. Ofta utgår man från ett antagande och detta antagande kan sedan få stöd genom direkta eller indirekta observationer. Einstein antog t.ex. att ljushasigheten i vakuum är konstant när han utvecklade sin speciella relativitetsteori, och denna har visat sig stämma mycket väl.

Från Tycho Brahes mycket exakta mätningar av planeten Mars' rörelse (slutet av 1500-talet) kunde Johannes Kepler (i början av 1600-talet) få fram tre lagar för planeternas rörelser. Samtidigt använde Gallileo Gallilei det nyuppfunna teleskopet för att göra astronomiska observationer. Han studerade även, både teoretiskt och experimentellt, kroppars rörelse.

Isaac Newton kunde senare (andra hälften av 1600-talet) "förklara" planeternas rörelser med hjälp av en lag, den universella gravitationslagen och nyutvecklad matematik (differentialkalkyl).

Den ovanstående utgör det centrala i utvecklingen av den moderna vetenskapliga metod som används i naturvetenskapen, se fråga [14237].

En annan viktig aspekt på fysik är att fysikaliska lagar inte är huggna i sten, utan de kan modifieras allteftersom vi gör bättre observationer.

Lagarna kan emellertid inte ändras hur fritt som helst, utan de måste alltid kunna reproducera alla befintliga mätresultat. Einsteins allmänna relativitetsteori beskriver gravitationen på ett utmärkt sätt, men den är mycket olik Newtons gravitationsteori. Det betyder inte att Newton hade fel, bara att det fanns begränsningar i giltigheten. Man använder t.ex. forfarande Newtons teori för att beräkna banor för rymdsonder.

I fysik använder man sig ofta av förenklade modeller som beskriver ett fysikaliskt fenomen med begränsade förutsättningar, se fråga [18296]. I kärnfysik betraktar man t.ex. ibland atomkärnan som en vätskedroppe och ibland som nukleoner som rör sig fritt i en potential (skalmodell). Modellerna är egentligen helt inkompatibla, men de är ändå av värde eftersom de båda "förklarar" olika egenskaper hos atomkärnor.

Och nu äntligen till din fråga:

Begreppet "förklarar" i texten ovan får man tolka så att man kan beskriva ett fenomen på en djupare nivå. Låt oss ta solens rörelse. Den dagliga rörelsen från öster till väster "förklaras" av att jorden roterar kring sin axel.

Solen rör sig även lite från väster till öster i förhållande till de avlägsna stjärnorna. Detta "förklaras" av att jorden rör sig ett varv runt solen på ett år. För att få ett A måste vi även kunna beskriva att den årliga rörelsen beskrivs av Newtons gravitationslag.

Den "wobblande" rörelsen du talar om uppkommer eftersom två kroppar rör sig i elliptiska banor kring den gemensamma tyngdpunkten. Om mass-skillnaden mellan kropparna är stor ligger den gemensamma tyngdpunkten nära den tyngre kroppens centrum. Detta betyder att den tyngre kroppen rör sig mycket lite.

Ett annat exempel är solsystemets uppbyggnad. Vi kan observera att planeterna alla rör sig åt samma håll och i ett plan. Detta kan "förklaras" genom modellen att solsystemet bildats genom att ett gasmoln dras samman av gravitationen. Bevarande av rörelsemängdsmomentet (se fråga [12527]) ger då upphov till en roterande skiva av gas och stoft. Denna bildar sedan planeterna i ett plan och rörelse åt samma håll.

I fråga [16776] beskrivs solsystemets rörelse i vintergatan och universum.
/Peter E 2016-02-24

Svar:
För ett icke rullande föremål på ett lutande plan omvandlas potentiell energi till rörelseenergi. Om vi kan borse från friktion kommer alla föremål att ha samma hastighet nedför planet:

mgh = mv²/2

v = sqrt(2gh)

Den viktigaste skillnaden om föremålet rullar är relativt tröghetsmoment. (Vi förutsätter att bollarna rullar utan friktionsförluster och glid.) Tröghetsmomentet beror av massfördelningen. Mycket massa nära ytan av bollen och stor radie ger högt tröghetsmoment och därmed mer rotationsenergi för en given rotationshastighet. Denna tas från den vanliga rörelseenergin, vilket saktar ner den linjära rörelsen.

Rullande föremål med högt tröghetsmoment rullar alltså långsammare än föremål med lågt tröghetsmoment. Bocciabollen är homogen av metall (Bocce). En innebandyboll är ihålig och av plast (Innebandyboll). Massfördelningen skulle ge ett högt tröghetsmoment för innebandybollen och lägre för bocciabollen. Densiteten är emellertid mycket högre för bocciabollen, så jag tror denna rullar saktare. Det hade varit enklare om bollarna varit av samma material och med samma radie.

Se fråga [20352] och [14738] för mer om rullande kulor.

I länk 1 och 2 finns tröghetsmomentet för några olika objekt. Om massan och radien är lika får vi följande för sluthastigheten:

kloss (ingen rotation): sqrt(2gh) = 1.41sqrt(gh)

boll: sqrt((10/7)gh) = 1.20sqrt(gh)

cylinder: sqrt((4/3)gh) = 1.15sqrt(gh)

ring: sqrt(1gh) = 1sqrt(gh)
/Peter E 2016-10-14

Svar:
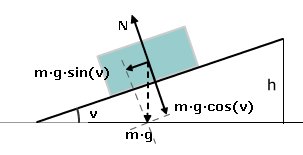
För att dra lådan uppför planet krävs en kraft som är lika med summan av friktionskraften µ·N=µ·m·g·cos(v) och tyngdkraftens komposant m·g·sin(v), alltså dragkraften, se länk 1 och nedanstående figur från länk 1:

F = µ·m·g·cos(v) + m·g·sin(v)

Potentiell energi på höjden h: mgh

Arbete: (µ·m·g·cos(v) + m·g·sin(v))·h/sin(v)

Verkningsgrad = e = Potentiell energi/Arbete

e = sin(v)/((µ·cos(v) + sin(v)) = 1/(µ·cot(v) + 1)

Låt oss se om detta är rimligt. Utan friktion (µ=0) ger e=1 som sig bör.

Om vinkeln v=0^o blir e=0. Om v=90^o blir e=1. Dessa extremfall motsvarar mycket friktion (lång sträcka, hög normalkraft) och ingen friktion (lådan dras vertikalt utan att röra planet).

Om v=45^o och µ=0.2 blir e=1/(0.2+1)=0.83.

Som du ser är det korrekt att stor vinkel ger högre verkningsgrad.

/Peter E 2016-11-22

Svar:
Intressant fråga Alvin! Vi är inte experter på hovrande helikoptrar, så vi fick börja med att studera information på webben. Där står inget om den stabilitet du talar om. Man får i stället intrycket att problemet är ganska komplicerat och att hovrande kräver skickligt samtidigt manipulerande av tre reglage. Länk 1 beskriver detaljerat de tre reglage man behöver för att hovra med en helikopter. Det tycks inte vara helt lätt.

Vi begränsar diskussionen till det viktigaste: lyftkraften. Denna beror i ett idealt system utan vind av rotorns varvtal, rotorbladens vinkel och luftens densitet.

Om vi antar att de första två är konstanta, så skulle man kunna tänka sig att luftens med höjden avtagande densitet skulle vara stabiliserade. Om helikoptern flyger högre är luftens densitet lägre, och lyftkraften minskar. Tvärtom, ger lägre höjd, högre luftdensitet och större lyftkraft.

Det borde alltså finnas en optimal höjd där lyftkraften är lika med helikopterns tyngd, vilket är kravet för att helikoptern skall hovra. Man kan beräkna luftens densitet med appen i länk 2. Densiteten på 10m och 20m höjd är 1.22382 respektive 1.22265 kg/m³. Skillnaden är alltså 0.00117 kg/m³ eller c:a en tusendel. Det är knappast troligt att denna lilla effekt kan vara förklaringen.

Hovring är emellertid stabilare nära marken på grund av den så kallade markeffekten (Ground_effect_(aerodynamics)). Luftströmmen från rotorn skapar ett övertryck när den träffar marken. Övertrycket ger ökad lyftkraft. Eftersom effekten avtar snabbt med ökande höjd bör man vänta sig en stabiliserande effekt vad gäller höjden. Problemet här är emellertid att detta endast fungerar på mycket låg höjd, ungefär ett rotorblad upp, och det är inte effekten du beskriver.

Lyftkraft visar hur man beräknar lyftkraften.

Här är några fler länkar:

https://www.rchelicopterfun.com/nose-in-hover.html

https://www.theguardian.com/notesandqueries/query/0,5753,-2666,00.html

https://www.decodedscience.org/why-is-it-so-difficult-to-hover-a-helicopter/22946

http://www.maunaloahelicopters.com/how-to-hover-a-helicopter/

http://www.dynamicflight.com/aerodynamics/ground_effect/
/Peter E 2018-03-22

Svar:
Alisya!

Såvitt jag förstår är du ute efter att bestämma tyngdaccelerationen g genom att mäta svängningstiden för en plan pendel.

Tyngdacceleration är inom klassisk mekanik den acceleration som är resultatet av kombinationen av gravitationsaccelerationen och den centrifugalacceleration som härrör från en kropps rotation, till exempel jordens rotation. Tyngdaccelerationen på jordytan, också kallad jordaccelerationen, varierar med latitud, mellan cirka 9,78 m/s² vid ekvatorn och 9,83 m/s² vid polerna.
(Tyngdacceleration)

Den formel du ger är korrekt men för en fysikalisk pendel. Problemet med denna är att uttrycket för perioden innehåller flera parametrar som är svåra att uppskatta, speciellt tröghetsmomentet I. Se PendelFysikalisk_pendel.

Man kan i stället använda sig av en enklare modell, en s.k. Matematisk pendel, se PendelMatematisk_pendel. Svängningstiden för en sådan härleds i fråga [14065]:

T = 2p&8730;(l/g)

Som du ser innehåller formeln T, l och g. Genom att mäta l och motsvarande T kan du alltså räkna ut ett värde på g.

För att få ett tillförlitligt svar bör du mäta tiden för flera pendelcykler (l), t.ex. 10-20 stycken. Du kan även göra mätningen med flera pendellängder (l) och ta medelvärdet på resultaten.

Se även fråga [4287].
/Peter E 2021-05-04