Vill du ha ett snabbt svar - sök i databasen
Nyckelord: ljus
64 träffar
Varför är himlen ibland blå och ibland röd?
Hej. Om det är av samma orsak som himlen ibland är röd som
den ibland är blå, borde den då inte också lika ofta vara
grön, då grön ligger mellan blå och röd i färgspektrat.
Vad beror annars de olika färgerna på?
/Mats L, Pauliskolan, Malmö 1997-11-20
Mycket intressant fråga! Svaret är att himlen
kan vara grön, det är bara det att det är sällsynt.
Låt oss försöka reda ut de olika färgerna:
Mitt på dagen är himlen blå. Det beror på att
solljuset sprids av luften, och blått ljus sprids
mer än rött och gult. Eftersom det är spritt
ljus, så är det också polariserat.
Försök:
Sätt på dig ett par polarisationssolglasögon. Titta
på en punkt 90 grader (ett kvarts varv) från solen.
Vrid på huvudet. Kan du se att himlen blir mörkare
när huvudet är i ett visst läge?
När solen håller på att gå ner, så har solljuset så lång
väg att gå igenom atmosfären, att det blå ljuset är helt
försvunnet (spritts bort). Det enda du ser då är det
röda ljuset som sprids - du har en vackert röd solnedgång.
I ett mellanläge kan man ibland se att himlen är grön, men det är, som sagt, ganska ovanligt.
Se även snackset Varför är himlen blå?![]() .
.
Jag undrar hur de stämplar som finns i vissa entrebiljetter mm fungerar (de som syns i UV-ljus).
/Johannes L, SÄG, Karlstad 1998-02-17
De innehåller ett fluorescerande ämne. När detta ämne träffas av ultraviolett ljus
så absorberas detta ljus medan ett annat ljus med längre våglängd sänds ut.
1998-02-23
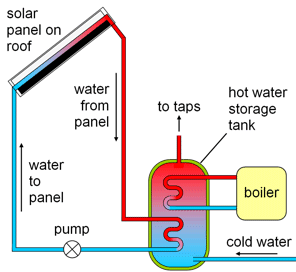
Solenergi
Kan man använda solenergi över hela världen? Vilka olika typer av solfångare finns det? Vad kostar det?
/Per L, Näsbydalskolan, Täby 1998-03-09
Solljusets betydelse för såväl naturliga processer på jorden som mänsklig verksamhet visar sig i att nästan all energiomsättning på jorden härrör från solen. Det enda andra energiutbytet alstras av radioaktiva ämnen, som driver kärnkraftverk (kärnenergi) samt svarar för en stor del av värmen i jordens innandöme (geotermisk energi).
Detta betyder att ca 95 % av världens energianvändning direkt eller indirekt utgörs av solenergi, till största delen lagrad i en eller annan form. Hit hör således de fossila bränslena, som utgör solenergi som lagrades för hundratals miljoner år sedan, biomassa som lagrats i år eller tiotals år i form av träd och annan växtlighet, samt jordvärme, där sommarens solinstrålning används för att producera varmvatten även på vintern. Vattenkraft är också lagrad solenergi - solinstrålningen skapar moln som ger regn i höglänta områden. Även vind- och vågenergi är ytterst solenergi eftersom rörelsen i atmosfär/hav även drivs av solinstrålningen. Dessa energislag behandlas vanligtvis dock för sig. När vi i dagligt tal talar om solenergi avser vi vanligen den direkta omvandling av solstrålningen till el och värme som sker i solceller och solfångare eller i stor skala i solkraftverk.
För en uthållig framtid behöver vi energisystem som endast bygger på
Solenergin är en enorm resurs. Solen utstrålar årligen cirka 3.51018 TWh varav 7.5108 TWh når jordytan. Av detta omvandlas knappt 0.06% i fotosyntesen och tas till vara av jordens växtlighet som energi i biomassa. Även den del av solenergin som omvandlas till vindar är mindre än en procent. Potentialen för direkt solenergianvändning
är därför stor jämfört med dessa båda andra förnybara
energikällor.
Världens kända och ekonomiskt utvinnbara tillgångar
av olja och gas, liksom uranreserverna för
dagens typ av kärnreaktorer, motsvarar den solinstrålning
som når jordens yta under bara några
dagar. Reserverna av kol motsvarar några veckors
solinstrålning.
Den energi som solljuset innehåller kan direkt användas på i princip tre olika sätt:
1
2
3
Priset på solenergi är fortfarande inte konkurrenskraftigt jämfört med andra energiformer utom för speciella tillämpningar.
Ta reda på. Hur är en vanlig solfångare konstruerad?
Projekt. Konstruera en enkel solfångare som kan användas för att ge varmvatten till duschen i ett fritidshus.
Se vidare
, Solenergi
 ,
,  .
.
Varför är himlen blå och solen gul?
Vad är färg?
Varför blir det färger i såpbubblor?
Hur uppstår färg?
/Teofil s, Falkenbergs gymnasie, Falkenberg 1998-10-12
Himlen är blå därför att solljuset sprids av luftmolekylerna, och det blå ljuset sprids effektivast. Ett mera detaljerat svar har du i fråga [13368].
Solen är inte gul om solstrålningen inte påverkas av atmosfären. Experiment: Håll ett vitt papper i solen när den står högt på himlen. Vilken färg får pappret? Ovansidan av sommarmoln är vita eftersom de reflekterar det vita solljuset effektivt.
När solen står lågt på himlen kan den uppfattas som gul eller orange. Det beror på att solljuset har lång väg genom atmosfären och att det kortvågiga (blå) ljuset sprids mer (se igen fråga [13368]). Tar vi bort blått ljus så ser solen mer gul/orange ut, se vänstra cirkeln i nedanstående figur där man har minskat det blå inslaget lite grann i en vit skiva. När solen står högt påverkas ljuset mycket lite av atmosfären, och solen ser vit ut. Problemet är att solen lyser så starkt att man inte kan titta på den: titta aldrig direkt på solen utan skydd - du kan skada ögat permanent mycket snabbt!. Om man är mycket försiktig kan man se solen även när den står högt på himlen genom ett tunnt moln. Molnet fungerar som ett gråfilter: det absorberar alla våglängder lika eftersom vattendropparna i molnet är stora jämfört med ljusets våglängd. Man kan då se att solen faktiskt är närmast vit. Se även länk 1.
Den färg vi uppfattar beror dels på strålningens våglängdsfördelning och dels ögats känslighet i de tre våglängdsband som tapparna är känsliga för, se fråga [13824]. Det mänskliga ögat har i stort sett utvecklats med solljus. Det vi uppfattar bör då nästan per definition vara vitt ljus.
Varför ritar man solen gul på en teckning? Gör man inget alls, ser det ut som man glömt något. Därför använder man den gula färgen, den verkar ljusast.
Färg är en egenskap hos ljuset, nämligen dess våglängd. Ljuset är ju en vågrörelse. Rött ljus har lång våglängd, blått ljus har kort våglängd, och andra färger däremellan. Man kan också ha en blandning av olika våglängder (färger). Experiment: Låt solljuset lysa genom ett glasprisma.
I en såpbubbla reflekteras (speglas) ljuset både i ytter- och innerväggen.De reflekterade strålarna kan samverka eller motverka varandra, beroendepå bubblans tjocklek och ljusets våglängd (färg). Fenomenet kallasinterferens.
Färg kan uppstå på många olika sätt.
Molekylspridning (blå himmel)
Absorption (saften är röd därför att bara det röda ljuset kommer igenom, det andra ljuset absorberas)
Emission (doppar du en tråd i saltlösning, och sticker in den i en ljuslåga blir det gult därför att natriumatomer sänder ut gult ljus)
Interferens (såpbubbla)
Detta är några exempel.

Varför skimrar plastfodralen till kassettband i olika färger?
Varför skimrar plastfodralen till kassettband i reflekterat ljus?
/erik w, östersund 1998-05-04
Du ser denna effekt så snart du har att göra med tunna genomskinliga skikt, som t.ex. plastfodral, såpbubblor eller ett tunnt lager bensin på vattnet.
Det beror på att en del av ljuset går igenom det tunna skiktet
och reflekteras, medan en del reflekteras redan i den första
ytan. Detta två ljusstrålar interfererar med varandra så att vissa färger förstärks och vissa släcks ut beroende på om vägskillnaden är ett jämnt antal våglängder eller ej. Eftersom skiktets tjocklek ofta varierar i olika punkter, så ser du ett färgat mönster.
Vad händer då med fotonerna (ljuspartiklarna) som släcks ut? Försvinner de bara? I så fall skulle lagen om energins bevarande inte vara uppfylld!
Ingen fara! Ljuset (energin) kan aldrig försvinna genom interferens. Vad som sker är att man får en omfördelning av strålningen, dvs de fotoner som saknas i de mörka områdena har i stället gått ut i en annan riktning. Antalet fotoner (energin) är alltså konstant, medan fördelningen i olika riktningar ändras genom interferensen.
Vissa fjärilar åstadkommer ett nästan självlysande intryck med hjälp av fjäll av exakt anpassad tjocklek, se länk 1:

Huygens princip
Jag går just nu tredje året på gymnasiet, och vi håller för tillfället på att arbeta med olika typer av vågrörelser, främst ljus. Ett av de försök vi har gjort går ut på att låta monokromt laserljus passera genom olika typer av spalter (enkelspalt, dubbelspalt, respektive gitter)
för att därefter träffa en skärm ett par meter bort. I samtliga fall uppstår som ni säkert känner till ljusfläckar symmetriskt kring centralpunkten på skärmen.
I läroboken beskrivs fenomenet så att spaltöppningarna, då de är tillräckligt små, böjer av ljusvågorna, vilka sedan interfererar med varandra varvid utsläckningar (noder) och förstärkningar (bukar) av ljuset uppstår.
De drar paralleller till två vattenvågor som interfererar med varandra och även de bildar förstärkningar respektive försvagningar. Emellertid talar de endast om dubbelspalter, respektive gitter. Men, hur applicerar man denna liknelse på försöket med enkelspalten, där man ju bara har en störningskälla för ljuset?
Min fysiklärare kunde inte svara på min fråga, så därför vänder jag mig till er och hoppas på ett intressant svar.
/Johan W, Nicolaiskolan, Helsingborg 1998-11-28
När man ska härleda interferensmönstret i en enkel spalt utgår
man från
en vågfront, utgör en källa till en halvsfärisk våg. Låter man
alla dessa vågor interferera med varandra, får man den nya vågfronten.
I fallet med enkelspalten, kan man skippa en dimension (den längs
spalten), och analysera problemet i två dimensioner. Man delar in
spalten i ett stort antal punkter, och låter sfäriska vågor från
dessa interferera. Man finner ganska enkelt, att ljuset får maxima
i riktningar (vinkel=v) som uppfyller:
sin(v) = nl/d
Ljusets våglängd = l, spaltvidden = d, n = heltal
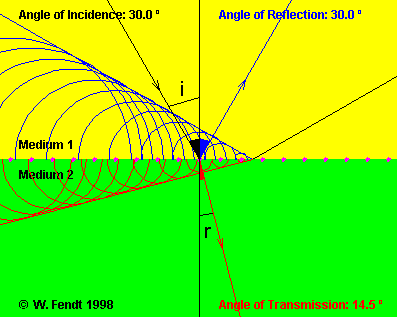
Man kan även härleda brytningslagen
n1 sin(i) = n2 sin(r)
med Huygens princip, se bilden nedan och java-appleten Huygen's Principle and Reflection and Refraction of Waves![]() . Lägg märke till att halvcirklarna är större i det gula mediet (brytningsindex n1=1) än i det gröna mediet (brytningsindex n2=2). Detta beror på att ljushastigheten v i ett medium med brytningsindex n ges av v=c/n, dvs ljusets hastighet är större i det gula mediet (c är som vanligt ljushastigheten i vakuum).
. Lägg märke till att halvcirklarna är större i det gula mediet (brytningsindex n1=1) än i det gröna mediet (brytningsindex n2=2). Detta beror på att ljushastigheten v i ett medium med brytningsindex n ges av v=c/n, dvs ljusets hastighet är större i det gula mediet (c är som vanligt ljushastigheten i vakuum).
Experiment 1: Dra med en vass kniv en skåra i ett papper.
Titta genom skåran på en skarp ljuskälla. En gatlykta med en
högtrycksnatriumlampa brukar vara bra (gult ljus). Fysiken finns också utanför labbet!
Experiment 2: Behövs: En gatlykta och ett träd eller en buske.
Håll för ena ögat och ställ dig så, att en gren precis täcker
gatlyktan. Titta nu på smågrenar nära denna punkt. Det lyser på
båda sidorna av grenen. Det kan alltså inte vara reflexion (spegling). Det är ljusböjning, som beror på att ljuset
är en vågrörelse. På sätt och vis omvändingen till enkelspalten.
Se länk 1 för mer om refraktion. General Physics Java Applets![]() innehåller Java applets för enkel- och dubbelspalt (se under optics).
innehåller Java applets för enkel- och dubbelspalt (se under optics).
Hur kan vissa saker bli självlysande?
/Anna K, Peder skrivare, varberg 1998-12-01
Med "självlysande" menar vi vanligen att något skickar ut "kallt ljus",
alltså utan att glöda. Med ett fint ord kallas fenomenet
När vi talar om
Kommer energin från en kemisk reaktion kallar vi det
En speciell typ av kemoluminiscens kallas
honungsskivling (en svamp).
Självlysande siffror lyser tack vare
energin från ett radioaktivt preparat, förr radium, numera tritium.
Det finns en del andra luminiscensfenomen, men de här är de viktigaste, se
/KS/lpe 1998-12-03
Tänk dig att man står vid en sjö eller en vik, då slår vågorna alltid upp mot stranden
oavsett hur det blåser Hur kommer det sig ??????
/Sofie B, nyhemskolan, ängelholm 1999-04-26
När vågorna kommer in på grundare vatten minskar våglängden och våghastigheten.
Då måste vågorna böjas av mot stranden. Fenomenet är tydligast på en
långgrund strand vid svag vind.
Det är samma sak som med ljusets brytning i till exempel glas. I glas
har ljuset mindre våglängd och lägre hastighet än i luft.
/KS 1999-05-06
Vad består ljuset av ?
varför har det alltid konstant hastighet oavsett
utgångshastighet?
När uppmättes ljushastigheten första gången?
Av vem? Hur gjorde han?
/Erik �, Lars Kaggskolan, kalmar 1999-08-27
Ljuset är en så kallad elektromagnetisk vågrörelse, men när ljuset
sänds ut och absorberas sker det i bestämda energipaket som kallas
fotoner.
Att ljusets hastighet alltid är konstant (i vakuum) är ett antagande
(så kallat postulat) man gör i den speciella relativitetsteorin.
Det kan därför inte förklaras inom ramen av relativitetsteorin.
Eftersom teorin tycks stämma väl med mätresultat, får vi helt
enkelt konstatera att naturen tycks vara så. Man kan också
undersöka saken med den nyare elektromagnetiska teorin
(kvantelektrodynamiken). Där beror ljusets hastighet på vissa intressanta egenskaper hos vakuum.
I många fall kan det vara svårt att säga vem som var först, men
inte i detta fallet. Det var en dansk astronom som hette Ole Römer.
Året var 1676 och platsen Paris. Han mätte tidpunkterna för
förmörkelser av jupitermånen Io, alltså tidpunkterna då Io
går in i och ut ur Jupiters skugga. Han fann en periodisk variation
med perioden lite mer än ett år. Avståndet till Jupiter varierar ju när
jorden går i sin bana runt solen. Han insåg att den periodiska variationen kunde förklaras om ljuset hade ändlig hastighet, och
han räknade ut ungefär rätt hastighet. Tänk att detta var över
300 år sedan. Ganska genialiskt, eller hur?
Slår man på ljus i Nationalencyklopedin![]() blir man lätt
blir man lätt
förvirrad. I texten beskrivs Ole Römers metod på ett sätt,
och i bildtexten på ett helt annat sätt. I själva verket är
det två oberoende metoder. Han använde sig av båda, och eftersom
de gav samma resultat, kunde han känna sig ganska säker på att han hade rätt.
Mera kan du läsa om det här: The Speed of Light![]() .
.
/KS/lpe 1999-10-15
Vad är det som bestämmer färgerna på ett norrsken?
Vad är det som bestämmer färgerna på ett norrsken?
/Pia S, Malmens friskola, Malmgerget 2000-01-26
Färgerna är spektrallinjer från syreatomer. I jordens magnetfält finns laddade partiklar som i spiralbanor åker fram och tillbaka mellan nord- och sydpol (strålningsbälten eller van Allen-bälten). Om en elektron från dessa bälten når tillräckligt långt ner kan det hända att den
kolliderar med en syremolekyl, som kan gå sönder i två syreatomer i högt energitillstånd.
Två energinivåer är intressanta för norrskenet. Det ena har en livstid av 1 sekund, och ger grönt ljus, och syreatomen
övergår till det andra tillståndet som har en livstid av 2 minuter, och ger rött ljus. Syreatomerna kan också gå ner i energi utan ljus genom kollisioner med andra molekyler. Därför uppträder norrsken bara där atmosfären är så tunn att kollisioner är sällsynta. Det är också
förklaringen till att det röda ljuset syns högre upp än det gröna. Om det rör sig om ett livligt norrsken kan man se gröna norrskensstrålar som lyser till kraftigt och sedan slocknar. Kvar blir ett diffust rött sken, som långsamt dör ut.
Ibland kan ljus från kväve uppträda, men ljuset från syreatomerna dominerar. Det gröna ljuset är vanligast.
Elektroner och protoner i strålningsbältena kommer från den s.k. solvinden som består av laddade partiklar som sänds ut från solens yta. Beroende på solaktiviteten varierar solvinden ganska mycket. I de allra nordligaste delarna av Sverige är norrsken ganska vanliga. I södra Sverige är norrsken ovanliga, och förekommer bara när solaktiviteten är mycket hög. Kraftiga strömmar av laddade partiklar orsakar, förutom norrsken, även magnetiska stormar som kan störa kommunikation och el-försörjning.
Se även Norrsken, IRF, Kiruna
 och Solvind
och Solvind .
.
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.
Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar

