Vill du ha ett snabbt svar - sök i databasen:
600 frågor / svar hittades
Varför är en frysskåpsdörr så trög att öppna igen, efter att man precis har stängt den?
Fråga:
Varför är en frysskåpsdörr så trög att öppna igen, efter att man precis har stängt den?
/Lina T, 2007-05-05
Varför är en frysskåpsdörr så trög att öppna igen, efter att man precis har stängt den?
/Lina T, 2007-05-05
Svar:
Det är så att man inte skall kunna nalla av glasspinnarna hela tiden :-).
Det är lufttrycket som håller igen dörren. Avkylningen av luften i frysen orsakar ett undertryck. Efter en stund (några minuter) utjämnas detta undertryck eftersom frysen inte är helt tät. Tryckutjämningen ger upphov till ett pysande ljud. Undertrycket ger upphov till en kraft som stänger dörren ordentligt.
Låt oss göra en uppskattning av hur stor kraften kan bli. Vi använder den allmänna gaslagen:
pV = nRT
p = trycket, V = volymen, n = antal mol, R = allmänna gaskonstanten,
T = absoluta temperaturen
Anta att rumstemperaturen är 20oC och temperaturen i frysen är -20oC. I gaslagen skall vi använda absoluta temperaturer, så temperaturerna blir Trum=273+20=293 K och Tfrys=273-20=253 K.
Vi kan skriva gaslagen som
p = (nR/V)T = konstantT
Om n är antal mol gas i frysen när dörren precis stängs, så är n och naturligtvis även V konstanta. Vi får
pfrys = konstantTfrys
prum = konstantTrum
Varav följer
pfrys = (Tfrys/Trum)prum
Normaltrycket i rummet är ungefär 105 Pa (N/m2) varför vi får
pfrys = (253/293)105 = 86348 Pa
Undertrycket blir alltså 100000-86348 = 14000 Pa
Om dörrens yta är 1 m2 så är alltså kraften från övertrycket hela 14000 N. Detta motsvarar en vikt på 1400 kg!
Detta låter ganska mycket (vi borde inta alls kunna få upp dörren), men vi har räknat lite väl optimistiskt. För det första hinner inte all luft i den kalla frysen bytas ut. Om vi har dörren öppen så länge att all luft bytts ut, kommer det i stället ta mycket lång tid att kyla ner luften, och rumsluft kommer att läcka in. Dessutom är handtaget placerat i kanten av dörren och inte i mitten. Hävstångslagen ger då att den erforderliga kraften blir hälften så stor.
En riktigt gammal horisontell frys ger inte stor effekt eftersom den kalla luften stannar i frysen - kall luft har ju högre densitet. En modern frys med plastbackar ger även den liten effekt eftersom ingen kall luft kommer in. En halvgammal öppen frys ger bäst effekt - den kalla luften formligen rinner ut när man öppnar dörren!
Enkelt experiment:
För att illustrera att kall luft ger undertryck: Sätt på korken på en tom PET-flaska och lägg flaskan i frysen. När flaskan är kall tar man ut den och lossar försiktigt på korken. Vad händer och varför?
/Peter E 2007-05-05
Det är så att man inte skall kunna nalla av glasspinnarna hela tiden :-).
Det är lufttrycket som håller igen dörren. Avkylningen av luften i frysen orsakar ett undertryck. Efter en stund (några minuter) utjämnas detta undertryck eftersom frysen inte är helt tät. Tryckutjämningen ger upphov till ett pysande ljud. Undertrycket ger upphov till en kraft som stänger dörren ordentligt.
Låt oss göra en uppskattning av hur stor kraften kan bli. Vi använder den allmänna gaslagen:
pV = nRT
p = trycket, V = volymen, n = antal mol, R = allmänna gaskonstanten,
T = absoluta temperaturen
Anta att rumstemperaturen är 20oC och temperaturen i frysen är -20oC. I gaslagen skall vi använda absoluta temperaturer, så temperaturerna blir Trum=273+20=293 K och Tfrys=273-20=253 K.
Vi kan skriva gaslagen som
p = (nR/V)T = konstantT
Om n är antal mol gas i frysen när dörren precis stängs, så är n och naturligtvis även V konstanta. Vi får
pfrys = konstantTfrys
prum = konstantTrum
Varav följer
pfrys = (Tfrys/Trum)prum
Normaltrycket i rummet är ungefär 105 Pa (N/m2) varför vi får
pfrys = (253/293)105 = 86348 Pa
Undertrycket blir alltså 100000-86348 = 14000 Pa
Om dörrens yta är 1 m2 så är alltså kraften från övertrycket hela 14000 N. Detta motsvarar en vikt på 1400 kg!
Detta låter ganska mycket (vi borde inta alls kunna få upp dörren), men vi har räknat lite väl optimistiskt. För det första hinner inte all luft i den kalla frysen bytas ut. Om vi har dörren öppen så länge att all luft bytts ut, kommer det i stället ta mycket lång tid att kyla ner luften, och rumsluft kommer att läcka in. Dessutom är handtaget placerat i kanten av dörren och inte i mitten. Hävstångslagen ger då att den erforderliga kraften blir hälften så stor.
En riktigt gammal horisontell frys ger inte stor effekt eftersom den kalla luften stannar i frysen - kall luft har ju högre densitet. En modern frys med plastbackar ger även den liten effekt eftersom ingen kall luft kommer in. En halvgammal öppen frys ger bäst effekt - den kalla luften formligen rinner ut när man öppnar dörren!
Enkelt experiment:
För att illustrera att kall luft ger undertryck: Sätt på korken på en tom PET-flaska och lägg flaskan i frysen. När flaskan är kall tar man ut den och lossar försiktigt på korken. Vad händer och varför?
/Peter E 2007-05-05
Man kan se på ett hangarfartyg att det fälls upp en skiva bakom ett jetplan som skall starta. Varför?
Grundskola_7-9: Kraft-Rörelse [15327]
Fråga:
Man kan se på ett hangarfartyg att det fälls upp en skiva bakom ett jetplan som skall starta. Varför?
Om jag tar en vattenslang med fullt tryck och närmar mig väggen. I vilket läge (nära väggen eller längst ifrån) gör slangen mest tryck bakåt?
/Madeliene H, Askersund, Åsbro 2007-05-24
Man kan se på ett hangarfartyg att det fälls upp en skiva bakom ett jetplan som skall starta. Varför?
Om jag tar en vattenslang med fullt tryck och närmar mig väggen. I vilket läge (nära väggen eller längst ifrån) gör slangen mest tryck bakåt?
/Madeliene H, Askersund, Åsbro 2007-05-24
Svar:
För att skydda personal och utrustning från jetstrålen från startande flygplan.
Det har ingen betydelse. Så snart vattnet lämnat slangen kan den inte påverka den. Kraften beror på vattnets utgångshastighet och hur mycket vatten som kommer ut per sekund.
Se även fråga 13586 (gäller båda frågorna).
/Peter E 2007-05-24
För att skydda personal och utrustning från jetstrålen från startande flygplan.
Det har ingen betydelse. Så snart vattnet lämnat slangen kan den inte påverka den. Kraften beror på vattnets utgångshastighet och hur mycket vatten som kommer ut per sekund.
Se även fråga 13586 (gäller båda frågorna).
/Peter E 2007-05-24
Hur många heliumballonger krävs för att lyfta en tjej på 25 kg?
Fråga:
Hej! Jag jobbar som lärare i en 2:a klass och idag läste vi en bok där en tjej flög iväg med ballonger. Klassen började diskutera om man faktiskt kunde göra detta på riktigt. Så min fråga är, är det möjligt att om man har tillräckligt med heliumballongern sväva iväg? Och i så fall det är en flicka som väger 25 kilo hur många helium ballonger krävs det för att hon ska lyfta och flyga iväg? Jag är väldigt tacksam för svar eftersom barnen nu är väldigt nyfikna på om man faktiskt kan göra så.
/Mia S, Stenkulaskolan, Malmö 2007-09-12
Hej! Jag jobbar som lärare i en 2:a klass och idag läste vi en bok där en tjej flög iväg med ballonger. Klassen började diskutera om man faktiskt kunde göra detta på riktigt. Så min fråga är, är det möjligt att om man har tillräckligt med heliumballongern sväva iväg? Och i så fall det är en flicka som väger 25 kilo hur många helium ballonger krävs det för att hon ska lyfta och flyga iväg? Jag är väldigt tacksam för svar eftersom barnen nu är väldigt nyfikna på om man faktiskt kan göra så.
/Mia S, Stenkulaskolan, Malmö 2007-09-12
Svar:
Hej Mia! Jodå, med tillräckligt många ballonger kommer flickan att sväva iväg. Nedan finns en överslagsräkning hur mycket ballonger det krävs. Räkningarna är inte helt triviala, men 2:a klassarna får lita på att räkningarna är korrekta.
EnligtArkimedes princip är lyftkraften lika med den undanträngda luftens vikt:
lyftkraft = volym(luftens densitet)g
Heliumet i ballongen ger en nedåtriktad kraft, så nettolyftkraften blir
nettolyftkraft = volym(luftens densitet - heliumets densitet)g
Vi har här bortsett från vikten hos ballongmaterialet (gummit). Tyngdkraften på en 25 kg flicka är
F = mg = 25g
Om vi sätter denna lika med nettolyftkraften får vi med V som totala ballongvolymen och d som densiteter:
25g = V(dluft - dhelium)g
dvs
V = 25/(dluft - dhelium) m3
Luftens densitet vid 20oC är c:a 1.2 kg/m3. Vad är då heliums densitet vid samma temperatur? Enligtgaslagen, allmänna innehåller en viss volym av en gas lika många mol oberoende av vilken gas det är. Densiteten skalar sig alltså som molekylvikten. Heliums molekylvikt är 4 och luftens 28.8. Heliums densitet blir alltså
dhelium = (4/28.8)1.2 = 0.17 kg/m3
Volymen som krävs blir alltså
V = 25/(1.2 - 0.17) m3 = 24 m3
Om en klotformig ballong har diametern 40 cm så blir radien r 0.2 m och volymen
4pr3/3 = 4p0.23/3 = 0.034 m3
Det krävs alltså 24/0.034 = c:a 700 ballonger!
Vi har här bortsett från två saker: vikten hos ballongmaterialet och det faktum att man om ballongen är gjord av ett elastiskt material får lite högre tryck och därmed högre densitet innuti ballongen. Detta därför att gummits elasticitet orsakar en kraft som trycker ihop den inneslutna gasen. Man kan komma ifrån denna effekt om man använder sig av icke elastiska plastballonger.
Ursäkta att detta blev lite tekniskt, men om man vill ha ett kvantitativt svar så går det nog inte att göra enklare. Det som behövs är alltså två enkla fysikaliska lagar, Arkimedes princip och Den allmänna gaslagen, som båda sedan länge är väl etablerade både experimentellt och teoretiskt.
Se även länk 1.
/Peter E 2007-09-12
Hej Mia! Jodå, med tillräckligt många ballonger kommer flickan att sväva iväg. Nedan finns en överslagsräkning hur mycket ballonger det krävs. Räkningarna är inte helt triviala, men 2:a klassarna får lita på att räkningarna är korrekta.
Enligt
lyftkraft = volym(luftens densitet)g
Heliumet i ballongen ger en nedåtriktad kraft, så nettolyftkraften blir
nettolyftkraft = volym(luftens densitet - heliumets densitet)g
Vi har här bortsett från vikten hos ballongmaterialet (gummit). Tyngdkraften på en 25 kg flicka är
F = mg = 25g
Om vi sätter denna lika med nettolyftkraften får vi med V som totala ballongvolymen och d som densiteter:
25g = V(dluft - dhelium)g
dvs
V = 25/(dluft - dhelium) m3
Luftens densitet vid 20oC är c:a 1.2 kg/m3. Vad är då heliums densitet vid samma temperatur? Enligt
dhelium = (4/28.8)1.2 = 0.17 kg/m3
Volymen som krävs blir alltså
V = 25/(1.2 - 0.17) m3 = 24 m3
Om en klotformig ballong har diametern 40 cm så blir radien r 0.2 m och volymen
4pr3/3 = 4p0.23/3 = 0.034 m3
Det krävs alltså 24/0.034 = c:a 700 ballonger!
Vi har här bortsett från två saker: vikten hos ballongmaterialet och det faktum att man om ballongen är gjord av ett elastiskt material får lite högre tryck och därmed högre densitet innuti ballongen. Detta därför att gummits elasticitet orsakar en kraft som trycker ihop den inneslutna gasen. Man kan komma ifrån denna effekt om man använder sig av icke elastiska plastballonger.
Ursäkta att detta blev lite tekniskt, men om man vill ha ett kvantitativt svar så går det nog inte att göra enklare. Det som behövs är alltså två enkla fysikaliska lagar, Arkimedes princip och Den allmänna gaslagen, som båda sedan länge är väl etablerade både experimentellt och teoretiskt.
Se även länk 1.
/Peter E 2007-09-12
Experiment med Arkimedes princip
Fråga:
Hur skall jag förklara Archimedes princip för mina elever i år 2? De är 7-8 år gamla. De vill veta varför båtar kan flyta medan andra saker sjunker.
/Ann-Charlotte K, Gustav Vasaskolan, Stockholm 2007-09-12
Hur skall jag förklara Archimedes princip för mina elever i år 2? De är 7-8 år gamla. De vill veta varför båtar kan flyta medan andra saker sjunker.
/Ann-Charlotte K, Gustav Vasaskolan, Stockholm 2007-09-12
Svar:
Hej Ann-Charlotte!
Det finns några exempel och resonemang om detta i tidigare frågor, seArkimedes princip . Flera av dessa svar är emellertid lite för avancerade för så unga forskare som du har. Man får då gå tillbaka till "basics". Vad är fysik och mer generellt naturvetenskap? Hur arbetar man i naturvetenskap?
Naturvetenskap bygger på experiment och observationer. För att bringa lite ordning i resultaten konstruerar vi hypoteser, modeller, teorier, principer eller lagar (egentligen samma sak men med ökande status/säkerhet). De teoretiska beskrivningarna är ofta matematiska och svåra att förstå - de kräver mycket ofta t.ex. differentialekvationer eller annan avancerad matematik.
Historiskt började naturvetenskap (t.ex. "de gamla grekerna") med observationer av naturen och föreställningar om hur världen var konstruerad som ofta var baserade på filosofiska resonemang: "jag tror det hänger ihop så här eftersom jag tycker det bör vara så". Ett exempel är planetbanor: man antog de var cirkulära utan att det fanns något stöd i observationerna. Man trodde också att jorden var världens medelpunkt, igen helt utan stöd i observationer.
Först på 1600-talet började man (framför allt Gallilei) göra systematiska experiment och observationer och att systematisera resultaten med hjälp av matematik. Mycket av matematiken utvecklades (t.ex. differentialkalkyl) genom att det fanns behov för den för att beskriva fysikaliska fenomen.
Olika fysikaliska lagar och teorier har olika dignitet eller status.Keplers lagar för planeternas rörelse kan t.ex. härledas från Newtons gravitationslag . Denna senare får därmed en högre status. På så sätt kan vi beskriva världen med ett rimligt antal fundamentala lagar.
Se vidarefysik och vetenskaplig metod .
Så, vad gör vi med dina unga forskare? Jag tycker att det bästa är att låta dem göra experiment och observera vad som händer. Om de kan dra några enkla slutsatser så är det bra, annars har de fått erfarenheter som de har nytta av när de är mer avancerade och återkommer till problemet.
Vad händer med en träbit respektive en bit järn? Försök om möjligt hitta föremål som har samma form och storlek. Vissa föremål sjunker i vatten och vissa flyter. Vad är det för skillnad på föremålen som sjunker och de som flyter? Förhoppningsvis kan eleverna få fram att om föremålen har samma storlek så sjunker de tunga medan de lätta flyter. Detta har att göra med begreppet densitet som är massa per volymsenhet. Ett föremål med högre densitet än vatten sjunker och ett föremål med lägre densitet flyter.
Hur kan båtar av järn flyta (se även fråga 12887)? Jo, de flyter eftersom det finns utrymmen i båten som innehåller luft. Luften väger mycket lite, så medeldensiteten kan vara mindre än vattnets. Det gäller alltså att konstruera båten så att vatten inte läcker in.
Tag en syltburk av glas och lägg några mynt i den. Ställ ner burken i vattnet. Om det inte är alltför många mynt (för mycket last) så flyter burken. Tag ur mynten. Nu kommer burken antagligen att tippa och ta in vatten. Den sjunker då trots att den har mindre last. Detta är anledningen till att tankbåtar aldrig går tomma - man fyller tankarna med vatten, s.k. barlast. Utan barlast skulle båten bli så instabil att den kan välta och ta in vatten.
För lite äldre elever kan man göra lite mer avancerade experiment: Kryt fast de olika föremålen i ett snöre och knyt fast andra ändan av snöret i en fjädervåg. Läs av utslaget när föremålet hänger i luften. Sänk ner föremålet i vatten och läs av igen. Föremålet har blivit lättare. Om föremålet flyter ger vågen utslaget noll. Om föremålet sjunker är skillnaden i avläsningarna lika oberoende av material (kom ihåg att vi förutsatte att föremålen har samma volym). Viktminskningen är enligt Arkimedes princip lika med den undanträngda vätskans vikt.
Som ett sista steg kan man beräkna föremålens volym genom att mäta storleken och räkna ut volymen. Detta förutsätter att föremålens form är regelbunden, t.ex. en cylinder eller en låda. Vattnets densitet är 1 g/cm3. Genom att multiplicera volymen i cm3 med vattnets densitet får vi fram hur mycket den undanträngda vattnet väger. Detta skall stämma med ovanstående viktminskning.
Hur kan man förstå Arkimedes princip i termer av krafter? Vattnet utövar ju ett tryck på alla ytor hos den nedsänkta kroppen. Krafter som verkar i horisontalled tar ut varandra av symmetriskäl - en nedsänkt kropp flyttar sig inte i sidled. Trycket på ovansidan är emellertid mindre än trycket på undersidan eftersom trycket beror av avståndet till ytan (ju djupare man dyker desto högre blir trycket). Om vi tänker oss att kroppen är en stående cylinder med basytan A och höjden h och en vätska med densiteten r så blir skillnaden i tryck mellan ovansidan och undersidan
rhg
Totala nettokraften uppåt blir eftersom tryckskillnaden verkar på ytan A:
rhgA = rvolymeng = (massan hos vätskan)g
Vilket är precis vad Arkimedes princip säger.
SeArchimedes för mer om Arkimedes och hans uppfinningar och fråga 12555 för ett annat lättobserverat fenomen.
/Peter E 2007-09-13
Hej Ann-Charlotte!
Det finns några exempel och resonemang om detta i tidigare frågor, se
Naturvetenskap bygger på experiment och observationer. För att bringa lite ordning i resultaten konstruerar vi hypoteser, modeller, teorier, principer eller lagar (egentligen samma sak men med ökande status/säkerhet). De teoretiska beskrivningarna är ofta matematiska och svåra att förstå - de kräver mycket ofta t.ex. differentialekvationer eller annan avancerad matematik.
Historiskt började naturvetenskap (t.ex. "de gamla grekerna") med observationer av naturen och föreställningar om hur världen var konstruerad som ofta var baserade på filosofiska resonemang: "jag tror det hänger ihop så här eftersom jag tycker det bör vara så". Ett exempel är planetbanor: man antog de var cirkulära utan att det fanns något stöd i observationerna. Man trodde också att jorden var världens medelpunkt, igen helt utan stöd i observationer.
Först på 1600-talet började man (framför allt Gallilei) göra systematiska experiment och observationer och att systematisera resultaten med hjälp av matematik. Mycket av matematiken utvecklades (t.ex. differentialkalkyl) genom att det fanns behov för den för att beskriva fysikaliska fenomen.
Olika fysikaliska lagar och teorier har olika dignitet eller status.
Se vidare
Så, vad gör vi med dina unga forskare? Jag tycker att det bästa är att låta dem göra experiment och observera vad som händer. Om de kan dra några enkla slutsatser så är det bra, annars har de fått erfarenheter som de har nytta av när de är mer avancerade och återkommer till problemet.
Vad händer med en träbit respektive en bit järn? Försök om möjligt hitta föremål som har samma form och storlek. Vissa föremål sjunker i vatten och vissa flyter. Vad är det för skillnad på föremålen som sjunker och de som flyter? Förhoppningsvis kan eleverna få fram att om föremålen har samma storlek så sjunker de tunga medan de lätta flyter. Detta har att göra med begreppet densitet som är massa per volymsenhet. Ett föremål med högre densitet än vatten sjunker och ett föremål med lägre densitet flyter.
Hur kan båtar av järn flyta (se även fråga 12887)? Jo, de flyter eftersom det finns utrymmen i båten som innehåller luft. Luften väger mycket lite, så medeldensiteten kan vara mindre än vattnets. Det gäller alltså att konstruera båten så att vatten inte läcker in.
Tag en syltburk av glas och lägg några mynt i den. Ställ ner burken i vattnet. Om det inte är alltför många mynt (för mycket last) så flyter burken. Tag ur mynten. Nu kommer burken antagligen att tippa och ta in vatten. Den sjunker då trots att den har mindre last. Detta är anledningen till att tankbåtar aldrig går tomma - man fyller tankarna med vatten, s.k. barlast. Utan barlast skulle båten bli så instabil att den kan välta och ta in vatten.
För lite äldre elever kan man göra lite mer avancerade experiment: Kryt fast de olika föremålen i ett snöre och knyt fast andra ändan av snöret i en fjädervåg. Läs av utslaget när föremålet hänger i luften. Sänk ner föremålet i vatten och läs av igen. Föremålet har blivit lättare. Om föremålet flyter ger vågen utslaget noll. Om föremålet sjunker är skillnaden i avläsningarna lika oberoende av material (kom ihåg att vi förutsatte att föremålen har samma volym). Viktminskningen är enligt Arkimedes princip lika med den undanträngda vätskans vikt.
Som ett sista steg kan man beräkna föremålens volym genom att mäta storleken och räkna ut volymen. Detta förutsätter att föremålens form är regelbunden, t.ex. en cylinder eller en låda. Vattnets densitet är 1 g/cm3. Genom att multiplicera volymen i cm3 med vattnets densitet får vi fram hur mycket den undanträngda vattnet väger. Detta skall stämma med ovanstående viktminskning.
Hur kan man förstå Arkimedes princip i termer av krafter? Vattnet utövar ju ett tryck på alla ytor hos den nedsänkta kroppen. Krafter som verkar i horisontalled tar ut varandra av symmetriskäl - en nedsänkt kropp flyttar sig inte i sidled. Trycket på ovansidan är emellertid mindre än trycket på undersidan eftersom trycket beror av avståndet till ytan (ju djupare man dyker desto högre blir trycket). Om vi tänker oss att kroppen är en stående cylinder med basytan A och höjden h och en vätska med densiteten r så blir skillnaden i tryck mellan ovansidan och undersidan
rhg
Totala nettokraften uppåt blir eftersom tryckskillnaden verkar på ytan A:
rhgA = rvolymeng = (massan hos vätskan)g
Vilket är precis vad Arkimedes princip säger.
Se
/Peter E 2007-09-13
Varför kyls ett spänt gummiband när spänningen upphör?
Fråga:
Hej
Om jag håller en tom ballong mot min läpp t.ex., känner jag en viss temperatur. Töjer jag sedan i ballongen och håller den mot läppen känner jag en högre temperatur. Låter jag sedan ballongen återgå till sin ursprungliga form känner jag direkt den ursprungliga temperaturen. Vad har skett?
/Ragnar J, Lärcentrum, Tanumshede 2007-11-30
Hej
Om jag håller en tom ballong mot min läpp t.ex., känner jag en viss temperatur. Töjer jag sedan i ballongen och håller den mot läppen känner jag en högre temperatur. Låter jag sedan ballongen återgå till sin ursprungliga form känner jag direkt den ursprungliga temperaturen. Vad har skett?
/Ragnar J, Lärcentrum, Tanumshede 2007-11-30
Svar:
Det går bra med ett gummiband också!
Gummi har ovanliga egenskaper och uppför sig så, seNatural_rubberElasticity . Uttänjning av gummi utvecklar värme och kontraktion kräver värme. Teoretiskt är det analogt med adiabatisk (utan värmeutbyte med omgivningen) expansion/kontraktion av en ideal gas - bara tvärt om (gasen värms vid kompression och kyls vid expansion).
För "vanliga" elastiska material (t.ex. metaller) lagras elasticitetsenergin elektrostatiskt. Det betyder att, bortsett för lite friktionsförluster, deformationsprocessen inte ändrar strukturen på materialet. Arbetet som går åt för att deformera materialet lagras som potentiell energi eftersom avståndet mellan atomerna ändras från det normala. Temperaturen ändras inte i processen (fortfarande bortsett från friktion).
Gummi har en annan stuktur. Det består av polymerer i form av långa trådar. Trådarna är i viloläget lösa och svänger som gitarrsträngar. När man spänner ett gummiband kan trådarna inte svänga längre. Trådarna avger sin kinetiska energi i form av värme. Gummibandet blir varmt. När spänningen tas bort sker det omvända: värme omvandlas till ordnade svängningar hos trådarna. Gummit kyls alltså ner. Elasticitetsenergin i gummi lagras alltså termiskt såväl som elektrostatiskt.
Experiment:
Häng upp en liten vikt i ett gummiband. Värm gummibandet med en hårtork och observera vad som händer. Till skillnad från de flesta material så blir gummibandet kortare med ökande temperatur. En del av värmeenergin får polymertrådarna i gummit att svänga mer, vilket medför att gummit kontraherar.
Nedanstående video demonstrerar på ett indirekt sätt denna negativa expansionskoefficient för gummiband:
Se ävenElasticity_(physics) .
/Peter E 2007-12-02
Det går bra med ett gummiband också!
Gummi har ovanliga egenskaper och uppför sig så, se
För "vanliga" elastiska material (t.ex. metaller) lagras elasticitetsenergin elektrostatiskt. Det betyder att, bortsett för lite friktionsförluster, deformationsprocessen inte ändrar strukturen på materialet. Arbetet som går åt för att deformera materialet lagras som potentiell energi eftersom avståndet mellan atomerna ändras från det normala. Temperaturen ändras inte i processen (fortfarande bortsett från friktion).
Gummi har en annan stuktur. Det består av polymerer i form av långa trådar. Trådarna är i viloläget lösa och svänger som gitarrsträngar. När man spänner ett gummiband kan trådarna inte svänga längre. Trådarna avger sin kinetiska energi i form av värme. Gummibandet blir varmt. När spänningen tas bort sker det omvända: värme omvandlas till ordnade svängningar hos trådarna. Gummit kyls alltså ner. Elasticitetsenergin i gummi lagras alltså termiskt såväl som elektrostatiskt.
Experiment:
Häng upp en liten vikt i ett gummiband. Värm gummibandet med en hårtork och observera vad som händer. Till skillnad från de flesta material så blir gummibandet kortare med ökande temperatur. En del av värmeenergin får polymertrådarna i gummit att svänga mer, vilket medför att gummit kontraherar.
Nedanstående video demonstrerar på ett indirekt sätt denna negativa expansionskoefficient för gummiband:
Se även
/Peter E 2007-12-02
Hur kan spröda blommor växa genom asfalt?
Gymnasium: Kraft-Rörelse - osmos [15599]
Fråga:
Hejsan!
Jag håller på och tar reda på hur det kommer sig att spröda blommor kan växa genom asfalt?
jag hittar ingen bra fakta om detta fenomen och vänder mig därför till er, har ni ngn förklaring? och gärna tips om var jag kan lära mig mer om detta?
/Jessica F, Jensen Gymnasium Södra, Stockholm 2008-02-05
Hejsan!
Jag håller på och tar reda på hur det kommer sig att spröda blommor kan växa genom asfalt?
jag hittar ingen bra fakta om detta fenomen och vänder mig därför till er, har ni ngn förklaring? och gärna tips om var jag kan lära mig mer om detta?
/Jessica F, Jensen Gymnasium Södra, Stockholm 2008-02-05
Svar:
Hej Jessica! Blommorna är inte så spröda som de ser ut! Cellväggarna kan bli riktigt styva genom något som kallas osmotiskt tryck. Jag hittar inget direkt om blommor och asfalt, men lite kan jag säga.
Det krävs för det första en liten springa i asfalten så att en tunn rot eller stjälk kan ta sig igenom. Sedan växer plantan, och stjälken kan bygga upp ett stort tryck genom osmos. Detta tryck kan lätt bli 10 atmosfärer, dvs motsvara trycket av en 100 meters vattenpelare.
Vad orsakar detta osmotiska tryck? Låt oss citera svenska Wikipedia:
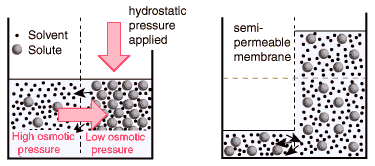
Transporten av vätskan orsakar ett övertryck som bland annat ger cellerna och därmed stjälken stadga, se nedanstående figur. Om den högra halvan i figuren är ett slutet område, t.ex. en cell, så kan vätskenivån inte höjas utan det byggs upp ett statiskt övertryck.
Se vidareOsmosis och nedanstående länkar.
Hej Jessica! Blommorna är inte så spröda som de ser ut! Cellväggarna kan bli riktigt styva genom något som kallas osmotiskt tryck. Jag hittar inget direkt om blommor och asfalt, men lite kan jag säga.
Det krävs för det första en liten springa i asfalten så att en tunn rot eller stjälk kan ta sig igenom. Sedan växer plantan, och stjälken kan bygga upp ett stort tryck genom osmos. Detta tryck kan lätt bli 10 atmosfärer, dvs motsvara trycket av en 100 meters vattenpelare.
Vad orsakar detta osmotiska tryck? Låt oss citera svenska Wikipedia:
Osmos är ett fysikaliskt och kemiskt fenomen som uppstår i ett semipermeabelt membran med vätskelösning på bägge sidor. Om membranet är genomträngligt för vätskan men inte för de salter som finns i vätskan (semipermeabelt), så kommer vätskan att strömma genom membranet till dess att osmotisk jämvikt uppstått. Osmos är en transport av lösningsämnen som drivs av en önskan att utjämna koncentrationer mellan upplösta ämnen. Om koncentrationerna skiljer sig åt kan vätskor och lösta ämnen tränga igenom tunna hinnor av oorganiskt eller organiskt material.
Transporten av vätskan orsakar ett övertryck som bland annat ger cellerna och därmed stjälken stadga, se nedanstående figur. Om den högra halvan i figuren är ett slutet område, t.ex. en cell, så kan vätskenivån inte höjas utan det byggs upp ett statiskt övertryck.
Se vidare
Att öppna glasburkar med metallock
Fråga:
Jag upplever att glasburkar med metallock går lättare att öppna om man spolar varmt vatten på. Vad är det som händer? Varför blir det så? Har det med att göra att metallocket sväller av värmen fortare än vad glaset gör och på så sätt lossnar det? Eller har det nåt med vakuum att göra att det upplöses när varmt vatten spolas på?
/Malin D, Lärarhögskolan, Stockholm 2008-02-22
Jag upplever att glasburkar med metallock går lättare att öppna om man spolar varmt vatten på. Vad är det som händer? Varför blir det så? Har det med att göra att metallocket sväller av värmen fortare än vad glaset gör och på så sätt lossnar det? Eller har det nåt med vakuum att göra att det upplöses när varmt vatten spolas på?
/Malin D, Lärarhögskolan, Stockholm 2008-02-22
Svar:
Malin! Du har bra idéer om orsaken. Framför allt två effekter kan spela in. Den första effekten om man värmer burken snabbt och den andra om man värmer den länge.
Termisk expansion (att material utvidgar sig när temperaturen blir högre): Metaller utvidgar sig mer än glas, se tabell i artikelnCoefficient_of_thermal_expansion . Lägg märke till att den öppna delen av locket expanderar som om den vore gjord av metallen. Utvidgningskoefficienten för hål är alltså lika med den för omgivningen, se länk 1 (stycket "Thermal expansion : expanding holes") för bevis. Dessutom leder metall värme bra, medan glas leder värme dåligt. Locket blir alltså varmare än glaset, vilket förhöjer effekten att locket expanderar relativt burken. Det blir då lättare att lossa locket dels för att kontakten med burken blir mindre, och dels för att eventuella tryckskillnader kan utjämnas (se nedan).
Att ett hål expanderar som omgivningen används i mekanisk industri för något som kallas krympförband (Shrink-fitting ).
Undertryck: Locket sätts på vid en förhöjd temperatur. För en ideal gas gäller den ideala gaslagen (se fråga [15294] ellerGas_laws ) att
pV = nRT
Vid konstant volym V och konstant mängd gas (n) är tryckändringen Dp proportionellt mot temperaturändringen DT. Vi får
Dp/p = DT/T
Om omgivningstemperaturen är 20oC = 293 K och temperaturen när locket sattes på 100oC får vi
Dp = p80/293 = 1.01310580/293 = 28000 N/m2 (pascal, Pa)
Om locket har en radie på 3 cm är ytan 32p, dvs c:a 30 cm2. Totala kraften på locket blir då
0.003028000 = 84 N. Detta motsvarar kraften som krävs för att lyfta c:a 8 kg, alltså en ganska stor kraft.
Om man värmer upp burken genom att hålla den länge under varmvattenskranen reduceras tryckskillnaden och därmed kraften. Observera alltså att tricket att hålla burken under varmvattenkranen hjälper för båda förklaringarna ovan!
Mikroskopisk förståelse av gaslagen:
Man kan förstå varför en viss mängd luft ger lägre tryck vid lägre temperatur. Temperatur är ett mått på molekylernas medelhastighet - om vi har låg temperatur så rör sig molekylerna långsamt. De kommer därför att kollidera med väggarna mindre ofta och mindre våldsamt än om temperaturen är hög. Det är just molekylernas kollektiva effekt på väggarna som makroskopiskt (i vår värld, till skillnad från molekylernas mikroskopiska värld) uppfattas som tryck.
/Peter E 2008-02-22
Malin! Du har bra idéer om orsaken. Framför allt två effekter kan spela in. Den första effekten om man värmer burken snabbt och den andra om man värmer den länge.
Termisk expansion (att material utvidgar sig när temperaturen blir högre): Metaller utvidgar sig mer än glas, se tabell i artikeln
Att ett hål expanderar som omgivningen används i mekanisk industri för något som kallas krympförband (
Undertryck: Locket sätts på vid en förhöjd temperatur. För en ideal gas gäller den ideala gaslagen (se fråga [15294] eller
pV = nRT
Vid konstant volym V och konstant mängd gas (n) är tryckändringen Dp proportionellt mot temperaturändringen DT. Vi får
Dp/p = DT/T
Om omgivningstemperaturen är 20oC = 293 K och temperaturen när locket sattes på 100oC får vi
Dp = p80/293 = 1.01310580/293 = 28000 N/m2 (pascal, Pa)
Om locket har en radie på 3 cm är ytan 32p, dvs c:a 30 cm2. Totala kraften på locket blir då
0.003028000 = 84 N. Detta motsvarar kraften som krävs för att lyfta c:a 8 kg, alltså en ganska stor kraft.
Om man värmer upp burken genom att hålla den länge under varmvattenskranen reduceras tryckskillnaden och därmed kraften. Observera alltså att tricket att hålla burken under varmvattenkranen hjälper för båda förklaringarna ovan!
Mikroskopisk förståelse av gaslagen:
Man kan förstå varför en viss mängd luft ger lägre tryck vid lägre temperatur. Temperatur är ett mått på molekylernas medelhastighet - om vi har låg temperatur så rör sig molekylerna långsamt. De kommer därför att kollidera med väggarna mindre ofta och mindre våldsamt än om temperaturen är hög. Det är just molekylernas kollektiva effekt på väggarna som makroskopiskt (i vår värld, till skillnad från molekylernas mikroskopiska värld) uppfattas som tryck.
/Peter E 2008-02-22
Newtons tredje rörelselag och jämvikt
Gymnasium: Kraft-Rörelse - Newtons rörelselagar [15642]
Fråga:
Newtons tredje lag säger att varje kraft har en lika stor motsatt riktad kraft. Detta borde betyda att den totala kraften blir noll, dvs att jämvikt råder. Men puttar man på ett föremål med en viss kraft (från friktion bortses), så får ju föremålet uppenbarligen en rörelse, och då kan ju inte jämvikt råda. Har tittat på Wikipedias artikel om detta (Newton's laws of motion), men artikeln förklarar inte denna, som det verkar, "motsägelse" att Newton III innebär jämvikt, och ändå blir det rörelse hos kropparna.
/Mårten B, Uppsala 2008-03-19
Newtons tredje lag säger att varje kraft har en lika stor motsatt riktad kraft. Detta borde betyda att den totala kraften blir noll, dvs att jämvikt råder. Men puttar man på ett föremål med en viss kraft (från friktion bortses), så får ju föremålet uppenbarligen en rörelse, och då kan ju inte jämvikt råda. Har tittat på Wikipedias artikel om detta (Newton's laws of motion), men artikeln förklarar inte denna, som det verkar, "motsägelse" att Newton III innebär jämvikt, och ändå blir det rörelse hos kropparna.
/Mårten B, Uppsala 2008-03-19
Svar:
Ibland formulerasNewtons tredje lag lite luddigt så att den är svårt att förstå. Den primära formuleringen i engelska Wikipedia
(Newton's_laws_of_motion ) är
dvs
Här är det tydligt att partikel A påverkas av en kraft i en viss riktning och partikel B av en lika stor kraft i motsatt riktning. Om vi först betraktar hela systemet A+B, så tar krafterna mycket riktigt ut varandra. Det är precis som det skall vara - man kan inte lyfta sig själv i håret!
Partikel A påverkas av en kraft och kommer att röra sig i kraftens riktning. Partikel B påverkas av en lika stor kraft i motsatt riktning, så partikeln kommer att röra sig i motsatt riktning i förhållande till A. Detta är vad i vissa sammanhang kallas rekyl: kulan flyger ut ur geväret och geväret får en knuff bakåt. Anledningen till att kulan rör sig fortare är att den är mycket lättare än geväret.
Newtons tredje lag är alltså egentligen en följd av den lag vi använder i den moderna formuleringen av Newtons tredje lag: bevarande av rörelsemängd (massahastighet, mv) - Newton använde inte rörelsemängd i sin framställning.
Newtons tredje lag gäller för alla krafter: både för fotboll och för månens och jordens rörelse. En ivägsparkad fotboll påverkar spelaren som sparkar. Både jorden och månen rör sig i elliptiska banor kring den gemensamma tyngdpunkten. I båda fallen ligger den gemensamma tyngdpunkten stilla om vi inte har någon annan yttre påverkan.
Se även fråga [18363].
/Peter E 2008-03-20
Ibland formuleras
(
Whenever a particle A exerts a force on another particle B, B simultaneously exerts a force on A with the same magnitude in the opposite direction.
dvs
Två kroppar, A och B, påverkar alltid varandra med lika stora men motriktade krafter.
Här är det tydligt att partikel A påverkas av en kraft i en viss riktning och partikel B av en lika stor kraft i motsatt riktning. Om vi först betraktar hela systemet A+B, så tar krafterna mycket riktigt ut varandra. Det är precis som det skall vara - man kan inte lyfta sig själv i håret!
Partikel A påverkas av en kraft och kommer att röra sig i kraftens riktning. Partikel B påverkas av en lika stor kraft i motsatt riktning, så partikeln kommer att röra sig i motsatt riktning i förhållande till A. Detta är vad i vissa sammanhang kallas rekyl: kulan flyger ut ur geväret och geväret får en knuff bakåt. Anledningen till att kulan rör sig fortare är att den är mycket lättare än geväret.
Newtons tredje lag är alltså egentligen en följd av den lag vi använder i den moderna formuleringen av Newtons tredje lag: bevarande av rörelsemängd (massahastighet, mv) - Newton använde inte rörelsemängd i sin framställning.
Newtons tredje lag gäller för alla krafter: både för fotboll och för månens och jordens rörelse. En ivägsparkad fotboll påverkar spelaren som sparkar. Både jorden och månen rör sig i elliptiska banor kring den gemensamma tyngdpunkten. I båda fallen ligger den gemensamma tyngdpunkten stilla om vi inte har någon annan yttre påverkan.
Se även fråga [18363].
/Peter E 2008-03-20
Beräkning av flykthastighet
Grundskola_7-9: Kraft-Rörelse - flykthastighet, Newtons gravitationslag, potential/potentiell energi [15646]
Fråga:
Hej Angående flykthastighet (fråga 3782) Jag är lärare på grundskolan och där använder vi inte integraler för beräkning av flykthastighet. Resonemanget är i stället att den potentiella energi en kropp har vid jordytan, i förhållande till jordens tyngdpunkt, är jordradiengm. Hela denna energi skall omvandlas till rörelseenergi mv2/2.
Vi finner naturligtvis att m förkortas "bort" och när vi löser ut
v=sqr(29,826,3471106)
blir flykthastigheten 11,19. På mostsvarande sätt gör vi för månen. Finns det någon invändning mot ovanstående resonemang? Undrar och hälsar Nils C
/Nils Eric C, Påarp, Helsingborg 2008-03-22
Hej Angående flykthastighet (fråga 3782) Jag är lärare på grundskolan och där använder vi inte integraler för beräkning av flykthastighet. Resonemanget är i stället att den potentiella energi en kropp har vid jordytan, i förhållande till jordens tyngdpunkt, är jordradiengm. Hela denna energi skall omvandlas till rörelseenergi mv2/2.
Vi finner naturligtvis att m förkortas "bort" och när vi löser ut
v=sqr(29,826,3471106)
blir flykthastigheten 11,19. På mostsvarande sätt gör vi för månen. Finns det någon invändning mot ovanstående resonemang? Undrar och hälsar Nils C
/Nils Eric C, Påarp, Helsingborg 2008-03-22
Svar:
Det är inte fel att räkna ut flykthastigheten från den potentiella energin vid jordytan (-mgR). Problemet är bara var man får uttrycket ifrån. Om det kommer från det vanliga uttrycket för potentiell energi nära jordytan mgh så är det fel. Det är bara en tillfällighet att uttrycken är så lika. Uttrycket mgh gäller bara om kraften är konstant, dvs nära marken. Den korrekta härledningen av uttrycket kräver att man integrerar, se nedan.
Låt oss först räkna ut flykthastigheten från ovanstående uttryck. Massan m på jordytan är alltså bunden med energin
(-mgR). För att massan skall vara fri från från jordens gravitation måste vi tillföra kinetisk energi med samma belopp. Massan har då potentiella energin noll, och är fri. Vi får
mv2/2 = mgR
dvs
v = sqrt(2gR) = sqrt(29.826.3710^6) = 11200 m/s = 11.2 km/s
Eftersom kraften på massan m varierar när vi tar den från jordytan till oändligheten, så kan man inte komma ifrån integration. Kraften mellan massorna m och M är
F = GmM/r2
där r är avståndet och G är gravitationskonstanten. Om vi integrerar kraften får vi potentialen
U = -GmM/r
Det gäller alltså att
U = -Fr
Detta beror på att avståndsberoendet hos kraften är som 1/r2. Vid jordytan r=R gäller alltså
U = -FR = -mgR
där vi eliminerat gravitationskonstanten G genom att i stället använda tyngdaccelerationen g (tyngdkraften vid jordytan på massan m är ju mg).
/Peter E 2008-03-23
Det är inte fel att räkna ut flykthastigheten från den potentiella energin vid jordytan (-mgR). Problemet är bara var man får uttrycket ifrån. Om det kommer från det vanliga uttrycket för potentiell energi nära jordytan mgh så är det fel. Det är bara en tillfällighet att uttrycken är så lika. Uttrycket mgh gäller bara om kraften är konstant, dvs nära marken. Den korrekta härledningen av uttrycket kräver att man integrerar, se nedan.
Låt oss först räkna ut flykthastigheten från ovanstående uttryck. Massan m på jordytan är alltså bunden med energin
(-mgR). För att massan skall vara fri från från jordens gravitation måste vi tillföra kinetisk energi med samma belopp. Massan har då potentiella energin noll, och är fri. Vi får
mv2/2 = mgR
dvs
v = sqrt(2gR) = sqrt(29.826.3710^6) = 11200 m/s = 11.2 km/s
Eftersom kraften på massan m varierar när vi tar den från jordytan till oändligheten, så kan man inte komma ifrån integration. Kraften mellan massorna m och M är
F = GmM/r2
där r är avståndet och G är gravitationskonstanten. Om vi integrerar kraften får vi potentialen
U = -GmM/r
Det gäller alltså att
U = -Fr
Detta beror på att avståndsberoendet hos kraften är som 1/r2. Vid jordytan r=R gäller alltså
U = -FR = -mgR
där vi eliminerat gravitationskonstanten G genom att i stället använda tyngdaccelerationen g (tyngdkraften vid jordytan på massan m är ju mg).
/Peter E 2008-03-23
Hur stora g-krafter utsätts en utförsåkare för?
Fråga:
Hej! Vilka krafter utsätts en utförsåkare för (g-kraft)? :)
/Sara B, Nya Läroverket, Luleå 2009-02-17
Hej! Vilka krafter utsätts en utförsåkare för (g-kraft)? :)
/Sara B, Nya Läroverket, Luleå 2009-02-17
Svar:
Sara! Tyngdkraften rakt nedåt, normalkraften vinkelrätt uppåt från backen, friktionkraften bakåt längst skidan och till slut luftmotståndet i en riktning motsatt färdriktningen.
Det var ett svar som frågan är formulerad. Men du menade antagligen vilken g-kraft en skidåkare kan utsättas för när hon svänger. Accelerationen a i en cirkelbana med radien r är
a = F/m = v2/r
där v är hastigheten. Låt oss anta hastigheten för en störtloppsåkare är 100 km/tim och krökningsradien r 50 m. Hastigheten 100 km/tim är 100000/3600 = 28 m/s, så vi får
a = 282/50 = 15.68 m/s2 = (15.68/9.81) g = 1.60 g.
Denna g-kraft är alltså riktad utåt, bort från krökningscentrum. Till denna komponent får man sedan addera tyngskraftkomponenten 1g riktad nedåt. Resultanten av dessa två blir då med hjälp av Pythagoras sats:
sqrt(11+1.61.6)g = 1.90g
Under korta perioder kan man nog tänka sig t.o.m. tvärare svängar än detta, så man kan förstå varför en störtloppsåkare är så trött efter bara ett par minuters åkning.
/Peter E 2009-02-18
Sara! Tyngdkraften rakt nedåt, normalkraften vinkelrätt uppåt från backen, friktionkraften bakåt längst skidan och till slut luftmotståndet i en riktning motsatt färdriktningen.
Det var ett svar som frågan är formulerad. Men du menade antagligen vilken g-kraft en skidåkare kan utsättas för när hon svänger. Accelerationen a i en cirkelbana med radien r är
a = F/m = v2/r
där v är hastigheten. Låt oss anta hastigheten för en störtloppsåkare är 100 km/tim och krökningsradien r 50 m. Hastigheten 100 km/tim är 100000/3600 = 28 m/s, så vi får
a = 282/50 = 15.68 m/s2 = (15.68/9.81) g = 1.60 g.
Denna g-kraft är alltså riktad utåt, bort från krökningscentrum. Till denna komponent får man sedan addera tyngskraftkomponenten 1g riktad nedåt. Resultanten av dessa två blir då med hjälp av Pythagoras sats:
sqrt(11+1.61.6)g = 1.90g
Under korta perioder kan man nog tänka sig t.o.m. tvärare svängar än detta, så man kan förstå varför en störtloppsåkare är så trött efter bara ett par minuters åkning.
/Peter E 2009-02-18
** Frågelådan är stängd för nya frågor tills vidare **
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.

Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.

Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar
