Vill du ha ett snabbt svar - sök i databasen
Nyckelord: idrottsfysik
15 träffar
Modell av ett 100-meterslopp
Fråga:
Hej!
Jag håller på och läser in kursen Fysik B och har problem med den matematiska rörelsebeskrivningen. I ett exempel som anges i kursboken är en matematisk modell över en 100-meterslöpares startförlopp:
v=10t-2.5t2 samtidigt som t är mellan 0 och 2 sekunder (1)
Fråga: Hur långt har löparen enligt modellen kommit efter 2 sekunder?
I lösningen som anges börjar man med att utgå från regeln: ds/dt=v.
Sedan anges, att s får bestämmas genom att göra en "primitiv funktion" till v, enligt:
s=5t2-2.5t3/3+C, där konstanten C sätts till 0 så att s=0 då t=0 (2)
Mitt problem är att jag inte alls förstår hur denna "primitiva funktion" till v har bestämts. Hur får man stegvis fram denna funktion??
Hemskt tacksam för svar!
/Susanna A, Stockholm 2009-04-17
Hej!
Jag håller på och läser in kursen Fysik B och har problem med den matematiska rörelsebeskrivningen. I ett exempel som anges i kursboken är en matematisk modell över en 100-meterslöpares startförlopp:
v=10t-2.5t2 samtidigt som t är mellan 0 och 2 sekunder (1)
Fråga: Hur långt har löparen enligt modellen kommit efter 2 sekunder?
I lösningen som anges börjar man med att utgå från regeln: ds/dt=v.
Sedan anges, att s får bestämmas genom att göra en "primitiv funktion" till v, enligt:
s=5t2-2.5t3/3+C, där konstanten C sätts till 0 så att s=0 då t=0 (2)
Mitt problem är att jag inte alls förstår hur denna "primitiva funktion" till v har bestämts. Hur får man stegvis fram denna funktion??
Hemskt tacksam för svar!
/Susanna A, Stockholm 2009-04-17
Svar:
Susanna! Låt oss först beräkna accelerationen a = dv/dt. Hastigheten v ges av din ekvation (1). Derivatan av v med avseende på tiden t blir då
a = dv/dt = 10-5t
Anledningen till att accelerationen skrivs så här är ju att allteftersom löparens hastighet ökar, så måste accelerationen minska1. Vi kan se att accelerationen enligt ovanstående modell är 0 vid t=2s. Då har löparen alltså uppnått sin sluthastighet. Om vi sätter in t=2s i (1) får vi slut(max)hastigheten 10 m/s.
Definitionen på hastighet är v=ds/dt. Hastigheten är alltså tidsderivatan vid en viss tidpunkt av den tillryggalagda sträckan. Se det så här: på den lilla tiden dt rör sig löparen sträckan ds. Hastighet är sträcka per tidsenhet alltså ds/dt.
Om vi våldför oss lite på matematiken kan vi se att ds=vdt. Hastigheten v ges ju som funktion av t av (1). Vi kan då beräkna v for en massa värden från 0 till 2s och multiplicera med dt. Dessa ds kan vi sedan summera för att få den sträcka löparen tillryggalagt.
Matematiken bakom ovanstående kallas Infinitesimalkalkyl och utvecklades av Newton och Leibniz på 1600-talet (seCalculus och fråga 16084 nedan). Formellt är ds/dt något som kallas derivata. För att beräkna s från funktionen ds/dt måste vi integrera. Det finns massor med regler för derivering och integration (som man får lära sig i matematiken), men det viktiga i detta sammanhang är att integration är omvändningen till derivering. Så om vi integrerar ds/dt med avseende på tiden så får vi sträckan s.
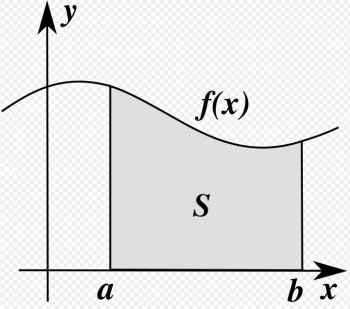
Bilden nedan från Wikimedia Commons visar att integralen helt enkelt är ytan S under en funktion f(x). Integralen är alltså en yta, och räknas ut som en oändlig summa av pyttesmala rektanglar.
Hur får man då fram funktionen (2) från (1)? Ja, man måste kunna lite integreringsregler. Oftast är det emellertid enklare att derivera än att integrera, så låt oss kontrollera om (1) är derivatan av (2):
(d/dt)(5t2-2.5t3/3+C) =
10t-2.5t2
vilket alltså stämmer bra.
Det är naturligtvis måttligt intressant att beräkna hur en hundrameterslöpare spinger, men exemplet vill visa hur man i fysiken arbetar med matematiska modeller som sedan kan jämföras med verkligheten. Här är till sist en tabell med värden på a, v och s beräknade med ovanstående uttryck och med antagandet att löparen från 2 sekunder och framåt har den konstanta hastigheten 10 m/s.
Hoppas detta hjälpte dig något!
1 Till skillnad från en raket som accelererar snabbare och snabbare. Skillnaden beror på att för raketen är den största delen av massan bränsle, och detta försvinner ju efter hand som raketen accelererar.
Susanna! Låt oss först beräkna accelerationen a = dv/dt. Hastigheten v ges av din ekvation (1). Derivatan av v med avseende på tiden t blir då
a = dv/dt = 10-5t
Anledningen till att accelerationen skrivs så här är ju att allteftersom löparens hastighet ökar, så måste accelerationen minska1. Vi kan se att accelerationen enligt ovanstående modell är 0 vid t=2s. Då har löparen alltså uppnått sin sluthastighet. Om vi sätter in t=2s i (1) får vi slut(max)hastigheten 10 m/s.
Definitionen på hastighet är v=ds/dt. Hastigheten är alltså tidsderivatan vid en viss tidpunkt av den tillryggalagda sträckan. Se det så här: på den lilla tiden dt rör sig löparen sträckan ds. Hastighet är sträcka per tidsenhet alltså ds/dt.
Om vi våldför oss lite på matematiken kan vi se att ds=vdt. Hastigheten v ges ju som funktion av t av (1). Vi kan då beräkna v for en massa värden från 0 till 2s och multiplicera med dt. Dessa ds kan vi sedan summera för att få den sträcka löparen tillryggalagt.
Matematiken bakom ovanstående kallas Infinitesimalkalkyl och utvecklades av Newton och Leibniz på 1600-talet (se
Bilden nedan från Wikimedia Commons visar att integralen helt enkelt är ytan S under en funktion f(x). Integralen är alltså en yta, och räknas ut som en oändlig summa av pyttesmala rektanglar.
Hur får man då fram funktionen (2) från (1)? Ja, man måste kunna lite integreringsregler. Oftast är det emellertid enklare att derivera än att integrera, så låt oss kontrollera om (1) är derivatan av (2):
(d/dt)(5t2-2.5t3/3+C) =
10t-2.5t2
vilket alltså stämmer bra.
Det är naturligtvis måttligt intressant att beräkna hur en hundrameterslöpare spinger, men exemplet vill visa hur man i fysiken arbetar med matematiska modeller som sedan kan jämföras med verkligheten. Här är till sist en tabell med värden på a, v och s beräknade med ovanstående uttryck och med antagandet att löparen från 2 sekunder och framåt har den konstanta hastigheten 10 m/s.
Vi ser alltså att löparen springer 100m på mellan 10 och 11s, dvs god svensk klass men ingen Usain Bolt :-)!
t a v s
-------------------------
0 10 0 0
1 5 7.5 4.2
2 0 10 13.3 3 0 10 23.3
4 0 10 33.3
5 0 10 43.3
6 0 10 53.3 7 0 10 63.3
8 0 10 73.3
9 0 10 83.3
10 0 10 93.3
11 0 10 103.3
Hoppas detta hjälpte dig något!
1 Till skillnad från en raket som accelererar snabbare och snabbare. Skillnaden beror på att för raketen är den största delen av massan bränsle, och detta försvinner ju efter hand som raketen accelererar.
Vad händer när man "curlar" i curling?
Fråga:
Hej! Skulle vilja veta vad som händer när man "curlar" i curling? Vad är det som gör att stenen glider bättre då?
/Hannes H, Alströmergymnasiet, Alingsås 2010-02-28
Hej! Skulle vilja veta vad som händer när man "curlar" i curling? Vad är det som gör att stenen glider bättre då?
/Hannes H, Alströmergymnasiet, Alingsås 2010-02-28
Svar:
Hannes! Intressant och aktuell fråga med tanke på lag Anette Norbergs insats i OS i Vancouver. Detaljerna för varför stenen "curlar" (avlänkas åt höger eller vänster i förhållande till den ursprungliga riktningen) är komplicerade och även kontroversiella. Vi behandlar detta i avsnittet mot slutet av svaret. Först en video om curling:
Vissa saker är man emellertid helt överens om:
1 Sopandet framför stenen skapar genom friktion värme som smälter isen och ger ett tunnt lager vatten. Detta minskar friktionen mellan stenen och isen.
2 Minskningen i friktion genom sopning medför dels att stenen går längre sträcka för en viss utgångshastighet och dels att den curlar (svänger) mindre.
3 Stenens curlande orsakas av friktionen mot isen och stenens rotation. Observera att man alltid sätter lite rotation på stenen: moturs om man vill att den curlar åt vänster och medurs om man vill ha en högerböj.
Till skillnad från andra sporter (t.ex. golf, bowling, skytte) kan man alltså påverka projektilens rörelse efter det att man släppt iväg den. Svårigheten är att man alltså får två effekter när man sopar: längre bana och mindre curl, och man måste besluta om en optimal kompromiss mellan effekterna.
SVTs kommentatorer vid OS-sändningarna från Vancouver spekulerade om vad resultatet skulle bli om det svenska damlaget skulle spela mot det svenska herrlaget. Man kom fram till att herrarna antagligen skulle vinna, men förklarade inte varför. Jag tror också herrarna skulle vinna helt enkelt för att de är tyngre och starkare, och kan på så sätt kontrollera stenen mer. Om man tittar på statistik för absoluta topp-curlare så har män c:a 90% och kvinnor c:a 80% lyckade stenar (slag).
Detaljerad förklaring till att stenen curlar
Låt oss börja med att göra ett enkelt experiment som du kan göra hemma. Ta ett köksglas (inte mormors finaste glas!) och leta upp ett jämnt, plant underlag, t.ex. en köksbänk. Vänd glaset upp-och-ner och skjut det längs bänken samtidigt som du sätter rotation på glaset, se vänstra bilden i nedanstående figur från Curling Science . Om du som i figuren roterar glaset medurs, så kommer glaset att avlänkas till vänster. Detta resultat är mycket förvånande för en curlare eftersom en curlingsten skulle avlänkas åt motsatt håll, se den högra bilden.
. Om du som i figuren roterar glaset medurs, så kommer glaset att avlänkas till vänster. Detta resultat är mycket förvånande för en curlare eftersom en curlingsten skulle avlänkas åt motsatt håll, se den högra bilden.
Varför reagerar glaset och curlingstenen olika på rotationen? Låt oss börja med att förklara varför glaset rör sig åt vänster. När glaset glider över bänken bromsas det up av en friktionskraft riktad rakt bakåt. Eftersom glasets tyngdpunkt ligger över bänkens plan, så kommer det att utsättas för ett vridmoment riktat bakåt. Trycket på framkanten av glaset blir då högre än trycket på bakkanten. Detta är samma effekt som att en bromsande bil får nosen nertryckt och en accelererande bil får nosen lyft. Eftersom glaset roterar får vi även en friktionskraft riktad åt vänster (friktionskraften är alltid motriktad rörelsen) i glasets framkant och en friktionskraft riktad åt höger i glasets bakkant. Eftersom normalkraften Fn enligt ovan är större i framkanten än i bakkanten blir friktionen större (se nedanstående formel), och vi kommer att få en nettokraft riktad åt vänster.
Varför uppför sig curlingsten annorlunda än glaset? För det första bör man veta att bottenytan på en curlingsten inte är plan, utan den har en skålformad fördjupning i mitten. Anläggningsytan mot isen är alltså en smal ring precis som för det upp-och-nervända glaset.
Skillnaden är att is smälter om den utsätts för högt tryck, se fasdiagrammet i fråga [12715]. Detta är skälet till att en kälke eller skridskor glider så bra på is - friktionen minskas genom ett tunnt vattenskikt. Precis som glaset utsätts stenen för en större normalkraft i framändan än i bakändan. I fallet curlingsten orsakar det högre trycket i framändan att friktionskoefficienten m minskar. Friktionskraften är ju
F = mFn (1)
Eftersom minskningen i friktionskoefficienten är större än ökningen i normalkraften kommer friktionskraften att bli mindre i framändan. Stenen kommer då att i stället böjas av åt höger.
Eftersom förklaringen bygger på att en del is smälts, så bör det ha betydelse vilken temperatur isen har. Om isens temperatur är mycket låg borde man vänta sig att den har svårare att smälta och att friktionen skulle bli större. I länk 1 sägs det om Scotts (Robert_Falcon_Scott ) sydpolsexpedition:
I What Puts the Curl in a Curling Stone? finns ovanstående förklaring till curlande och referenser till fyra vetenskapliga artiklar från Canadian Journal of Physics om olika aspekter på curling. The motion of curling rocks: Experimental investigation and semi-phenomenological description
finns ovanstående förklaring till curlande och referenser till fyra vetenskapliga artiklar från Canadian Journal of Physics om olika aspekter på curling. The motion of curling rocks: Experimental investigation and semi-phenomenological description är en senare artikel av samma författare. I den visas tydligt (men ganska svårgenomträngligt) att ovanstående modell är i stort sett korrekt även om vissa detaljer är oklara. Speciellt gäller detta hur stenen växelverkar med underlaget: växelverkar den med en fix isskiva eller med det rörliga vattnet under stenen? En annan effekt som är svår att förklara är att storleken av curl är i stort sett oberoende av stenens rotationshastighet. Intuitivt väntar man sig att en sten som roterar snabbare curlar mer.
är en senare artikel av samma författare. I den visas tydligt (men ganska svårgenomträngligt) att ovanstående modell är i stort sett korrekt även om vissa detaljer är oklara. Speciellt gäller detta hur stenen växelverkar med underlaget: växelverkar den med en fix isskiva eller med det rörliga vattnet under stenen? En annan effekt som är svår att förklara är att storleken av curl är i stort sett oberoende av stenens rotationshastighet. Intuitivt väntar man sig att en sten som roterar snabbare curlar mer.
I artikeln Comment on the motion of a curling rock framförs en annan modell där inte "våt friktion" (minskande friktionskoefficient) utan "torr friktion" (formel 1 ovan med konstant friktionskoefficient) används. Artikeln är emellertid inte av god kvalité, och slutsatserna är dubiösa.
framförs en annan modell där inte "våt friktion" (minskande friktionskoefficient) utan "torr friktion" (formel 1 ovan med konstant friktionskoefficient) används. Artikeln är emellertid inte av god kvalité, och slutsatserna är dubiösa.
Tester av modellerna
Det vore intressant att testa hur glaset uppför sig på is. Är det någon som har tillgång till mycket jämn is skulle jag vara tacksam om ni ville kummunicera era observationer till mig.
Ett annat experiment som är svårare att åstadkomma är att be ismakarna skruva upp kylningen till max. Skulle det gå att få ner temperaturen så mycket att man inte får någon smältning? Om det går skulle man få några mycket förvånade curlare: stenarna skulle bli mycket korta och curla åt fel håll :-)!
Sopforskning
Sopandet är uppenbarligen en mycket viktig del av curling eftersom detta är lagets möjlighet att påverka stenens bana sedan den släppts. Curling, Olympic training and ice friction fundamentals är ett anslag till några forskare för att förbättra chanserna för det brittiska damlandslaget att försvara sitt guld från 2002 i Turin 2006. Tydligen räckte inte pengarna, för som känt så vann ju lag Norberg!
är ett anslag till några forskare för att förbättra chanserna för det brittiska damlandslaget att försvara sitt guld från 2002 i Turin 2006. Tydligen räckte inte pengarna, för som känt så vann ju lag Norberg!
Vidare studier
Det finns som synes mycket i curling som är av fysikaliskt intresse, och då har vi inte tagit upp kollisioner mellan stenar och bevarandet av rörelsemängd och rörelseenergi.
För mer om curling se Wikipedia-artiklarna på engelska (Curling ) och på svenska (Curling ). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games
). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games . Länk 2 ger en alternativ förklaring.
. Länk 2 ger en alternativ förklaring.
Hannes! Intressant och aktuell fråga med tanke på lag Anette Norbergs insats i OS i Vancouver. Detaljerna för varför stenen "curlar" (avlänkas åt höger eller vänster i förhållande till den ursprungliga riktningen) är komplicerade och även kontroversiella. Vi behandlar detta i avsnittet mot slutet av svaret. Först en video om curling:
Vissa saker är man emellertid helt överens om:
1 Sopandet framför stenen skapar genom friktion värme som smälter isen och ger ett tunnt lager vatten. Detta minskar friktionen mellan stenen och isen.
2 Minskningen i friktion genom sopning medför dels att stenen går längre sträcka för en viss utgångshastighet och dels att den curlar (svänger) mindre.
3 Stenens curlande orsakas av friktionen mot isen och stenens rotation. Observera att man alltid sätter lite rotation på stenen: moturs om man vill att den curlar åt vänster och medurs om man vill ha en högerböj.
Till skillnad från andra sporter (t.ex. golf, bowling, skytte) kan man alltså påverka projektilens rörelse efter det att man släppt iväg den. Svårigheten är att man alltså får två effekter när man sopar: längre bana och mindre curl, och man måste besluta om en optimal kompromiss mellan effekterna.
SVTs kommentatorer vid OS-sändningarna från Vancouver spekulerade om vad resultatet skulle bli om det svenska damlaget skulle spela mot det svenska herrlaget. Man kom fram till att herrarna antagligen skulle vinna, men förklarade inte varför. Jag tror också herrarna skulle vinna helt enkelt för att de är tyngre och starkare, och kan på så sätt kontrollera stenen mer. Om man tittar på statistik för absoluta topp-curlare så har män c:a 90% och kvinnor c:a 80% lyckade stenar (slag).
Detaljerad förklaring till att stenen curlar
Låt oss börja med att göra ett enkelt experiment som du kan göra hemma. Ta ett köksglas (inte mormors finaste glas!) och leta upp ett jämnt, plant underlag, t.ex. en köksbänk. Vänd glaset upp-och-ner och skjut det längs bänken samtidigt som du sätter rotation på glaset, se vänstra bilden i nedanstående figur från Curling Science
Varför reagerar glaset och curlingstenen olika på rotationen? Låt oss börja med att förklara varför glaset rör sig åt vänster. När glaset glider över bänken bromsas det up av en friktionskraft riktad rakt bakåt. Eftersom glasets tyngdpunkt ligger över bänkens plan, så kommer det att utsättas för ett vridmoment riktat bakåt. Trycket på framkanten av glaset blir då högre än trycket på bakkanten. Detta är samma effekt som att en bromsande bil får nosen nertryckt och en accelererande bil får nosen lyft. Eftersom glaset roterar får vi även en friktionskraft riktad åt vänster (friktionskraften är alltid motriktad rörelsen) i glasets framkant och en friktionskraft riktad åt höger i glasets bakkant. Eftersom normalkraften Fn enligt ovan är större i framkanten än i bakkanten blir friktionen större (se nedanstående formel), och vi kommer att få en nettokraft riktad åt vänster.
Varför uppför sig curlingsten annorlunda än glaset? För det första bör man veta att bottenytan på en curlingsten inte är plan, utan den har en skålformad fördjupning i mitten. Anläggningsytan mot isen är alltså en smal ring precis som för det upp-och-nervända glaset.
Skillnaden är att is smälter om den utsätts för högt tryck, se fasdiagrammet i fråga [12715]. Detta är skälet till att en kälke eller skridskor glider så bra på is - friktionen minskas genom ett tunnt vattenskikt. Precis som glaset utsätts stenen för en större normalkraft i framändan än i bakändan. I fallet curlingsten orsakar det högre trycket i framändan att friktionskoefficienten m minskar. Friktionskraften är ju
F = mFn (1)
Eftersom minskningen i friktionskoefficienten är större än ökningen i normalkraften kommer friktionskraften att bli mindre i framändan. Stenen kommer då att i stället böjas av åt höger.
Eftersom förklaringen bygger på att en del is smälts, så bör det ha betydelse vilken temperatur isen har. Om isens temperatur är mycket låg borde man vänta sig att den har svårare att smälta och att friktionen skulle bli större. I länk 1 sägs det om Scotts (
Another key factor when considering the slipperiness of ice is temperature. Captain Scott noted during his Antarctic travels that once the temperature fell below -35 degrees C it become incredibly hard to pull sleds through the snow. This was because the heat produced by the friction between sled and snow was not enough to warm the ice to its melting point (0 degrees C) so no lubricating melt water was produced. Scott and his companions may as well have been pulling their sleds through sand. The closer the temperature of the ice is to its melting point the more melt lubricant is produced by sliding and the more slippery ice becomes.
I What Puts the Curl in a Curling Stone?
I artikeln Comment on the motion of a curling rock
Tester av modellerna
Det vore intressant att testa hur glaset uppför sig på is. Är det någon som har tillgång till mycket jämn is skulle jag vara tacksam om ni ville kummunicera era observationer till mig.
Ett annat experiment som är svårare att åstadkomma är att be ismakarna skruva upp kylningen till max. Skulle det gå att få ner temperaturen så mycket att man inte får någon smältning? Om det går skulle man få några mycket förvånade curlare: stenarna skulle bli mycket korta och curla åt fel håll :-)!
Sopforskning
Sopandet är uppenbarligen en mycket viktig del av curling eftersom detta är lagets möjlighet att påverka stenens bana sedan den släppts. Curling, Olympic training and ice friction fundamentals
Vidare studier
Det finns som synes mycket i curling som är av fysikaliskt intresse, och då har vi inte tagit upp kollisioner mellan stenar och bevarandet av rörelsemängd och rörelseenergi.
För mer om curling se Wikipedia-artiklarna på engelska (
 ). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games
). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games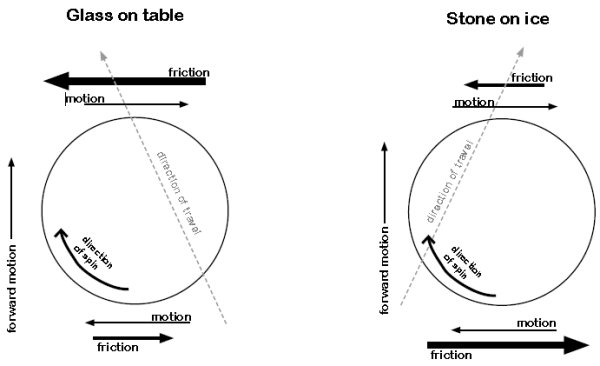
Vid backhoppning borde inte massan spela någon roll för hastigheten vid själva uthoppet (väl?).
Fråga:
Vid backhoppning borde inte massan spela någon roll för hastigheten vid själva uthoppet (väl?). Varför är det då en "trend" för backhoppare att de ska var så små som möjligt? Är det för att minska luftmotståndet?
/Sara L, Fredrikabremer gymnasiet, Haninge 2010-04-07
Vid backhoppning borde inte massan spela någon roll för hastigheten vid själva uthoppet (väl?). Varför är det då en "trend" för backhoppare att de ska var så små som möjligt? Är det för att minska luftmotståndet?
/Sara L, Fredrikabremer gymnasiet, Haninge 2010-04-07
Svar:
Sara! Intressant fråga, speciellt med tanke på tidigare svar om störtlopp! Jo, massan har betydelse för uthoppshastigheten. Se fråga [869] där det visas att hastigheten för en tyngre störtloppsåkare är större än för en mindre.
Hur kan det då komma sig att de bästa backhopparna ofta är små och lätta? En antydan får man om man jämför dräkterna. En störtloppsåkare har en tätsittande dräkt för att minimera luftmotståndet, medan en backhoppare har breda skidor och en dräkt som är "fem nummer för stor". Det är alltså inte farten i backen som bestämmer hopplängden utan förmågan att sväva långt i luften. För detta behöver man liten vikt och stor yta. Den stora ytan åstadkommer man dels med en väl tilltagen dräkt och dels med den s.k. V-stilen (Jan Boklöv,V-style ) som ger mer lyftkraft på kroppen eftersom den inte skuggas av skidorna - större "vinge" ger större lyftkraft. Hopplängden bestäms alltså till en stor del av aerodynamiken i luften.
En annan aspekt som gör farten i backen mindre utslagsgivande är att en stor del av uthoppshastigheten kommer från ett väl tajmat uthopp. Det är här och i förmågan att hålla kropp och skidor i en effektiv vinkel som skiljer bra hoppare från mindre bra.
Se vidare Backhoppning och
och Ski_jumping . Bilden nedan är från Wikimedia Commons.
/fa2010_4
Sara! Intressant fråga, speciellt med tanke på tidigare svar om störtlopp! Jo, massan har betydelse för uthoppshastigheten. Se fråga [869] där det visas att hastigheten för en tyngre störtloppsåkare är större än för en mindre.
Hur kan det då komma sig att de bästa backhopparna ofta är små och lätta? En antydan får man om man jämför dräkterna. En störtloppsåkare har en tätsittande dräkt för att minimera luftmotståndet, medan en backhoppare har breda skidor och en dräkt som är "fem nummer för stor". Det är alltså inte farten i backen som bestämmer hopplängden utan förmågan att sväva långt i luften. För detta behöver man liten vikt och stor yta. Den stora ytan åstadkommer man dels med en väl tilltagen dräkt och dels med den s.k. V-stilen (Jan Boklöv,
En annan aspekt som gör farten i backen mindre utslagsgivande är att en stor del av uthoppshastigheten kommer från ett väl tajmat uthopp. Det är här och i förmågan att hålla kropp och skidor i en effektiv vinkel som skiljer bra hoppare från mindre bra.
Se vidare Backhoppning
 och
och /fa2010_4

Stora störtloppsåkare, igen
Fråga:
Fråga angående ”869”, där ni diskuterar massans betydelse för en störtloppsåkare.
I svaret påstås att en tyngre åkare får en högre hastighet med följande resonemang:
”Kraften som drar skidåkaren nedåt är ju proportionell mot massan, medan kraften som bromsar (luftmotståndet) är proportionell mot ytan. Vi får allstå en större kraft för den tyngre skidåkaren, medan luftmotståndet inte ökar lika mycket. Så om allt annat är lika så har en tyngre åkare en fördel.”
Jag förstår inte resonemanget kring hur en större kraft ger en större hastighet...
MITT RESONEMANG:
Hänvisningen är således till Newtons andra lag: F = ma.
Ett större föremål får ju en större kraft. Men: Detta är i mina ögon inte samma sak som att föremålet får en högre hastighet - det är ju en större massa som ska accelereras.
Galileis lag ger att två föremål som faller från samma höjd faller lika fort oberoende av vikt givet att fritt fall föreligger. Detta trots att det tyngre föremålet påverkas av en större kraft. I vardagen har vi inte fritt fall, utan ett motstånd. Men det blir inte med nödvändighet mindre om massan ökar.
På motsvarande sätt menar jag att skidåkaren kommer att omsätta lägesenergi i rörelseenergi: mgh = 0,5mv^2, dvs massan spelar ingen roll om luftmotståndet och friktionen från underlaget försummas (givet att åkaren inte ”stakar”).
Enligt det resonemanget att en tyngre åkare skulle vara snabbare, så måste det innebära att han får ett mindre motstånd. Jag har svårt att se hur luftmotståndet skulle minska med massan (vilket inte heller påstås). Återstår att den tyngre åkaren skulle ha mindre friktion, trots att friktionen är proportionell mot normalkraften (som beror av massan). Det skulle möjligen kunna vara sant om åkaren med sin större massa trycker ner snön och därmed påverkar friktionstalet till sin fördel (vilket är tveksamt i en välpreparerad backe).
Min förklaring till att en tyngre åkare skulle kunna ha en fördel är följande:
Utförsåkning är en krävande sport. Det är jobbigt att krypa ihop i störtloppsställning. Det krävs stora krafter för att kunna hålla emot i svängarna. Det gynnar en fysiskt vältränad person med stor muskelmassa. Att lägga på sig muskelmassa ger en större vikt. Kraftfullheten som åkare ger en större effekt än den uppbromsande friktionen från en ökad massa, varför en tyngre åkare borde ha fördel (förutsatt att massan sitter på rätt ställe).
/Philip L, 2015-12-08
Fråga angående ”869”, där ni diskuterar massans betydelse för en störtloppsåkare.
I svaret påstås att en tyngre åkare får en högre hastighet med följande resonemang:
”Kraften som drar skidåkaren nedåt är ju proportionell mot massan, medan kraften som bromsar (luftmotståndet) är proportionell mot ytan. Vi får allstå en större kraft för den tyngre skidåkaren, medan luftmotståndet inte ökar lika mycket. Så om allt annat är lika så har en tyngre åkare en fördel.”
Jag förstår inte resonemanget kring hur en större kraft ger en större hastighet...
MITT RESONEMANG:
Hänvisningen är således till Newtons andra lag: F = ma.
Ett större föremål får ju en större kraft. Men: Detta är i mina ögon inte samma sak som att föremålet får en högre hastighet - det är ju en större massa som ska accelereras.
Galileis lag ger att två föremål som faller från samma höjd faller lika fort oberoende av vikt givet att fritt fall föreligger. Detta trots att det tyngre föremålet påverkas av en större kraft. I vardagen har vi inte fritt fall, utan ett motstånd. Men det blir inte med nödvändighet mindre om massan ökar.
På motsvarande sätt menar jag att skidåkaren kommer att omsätta lägesenergi i rörelseenergi: mgh = 0,5mv^2, dvs massan spelar ingen roll om luftmotståndet och friktionen från underlaget försummas (givet att åkaren inte ”stakar”).
Enligt det resonemanget att en tyngre åkare skulle vara snabbare, så måste det innebära att han får ett mindre motstånd. Jag har svårt att se hur luftmotståndet skulle minska med massan (vilket inte heller påstås). Återstår att den tyngre åkaren skulle ha mindre friktion, trots att friktionen är proportionell mot normalkraften (som beror av massan). Det skulle möjligen kunna vara sant om åkaren med sin större massa trycker ner snön och därmed påverkar friktionstalet till sin fördel (vilket är tveksamt i en välpreparerad backe).
Min förklaring till att en tyngre åkare skulle kunna ha en fördel är följande:
Utförsåkning är en krävande sport. Det är jobbigt att krypa ihop i störtloppsställning. Det krävs stora krafter för att kunna hålla emot i svängarna. Det gynnar en fysiskt vältränad person med stor muskelmassa. Att lägga på sig muskelmassa ger en större vikt. Kraftfullheten som åkare ger en större effekt än den uppbromsande friktionen från en ökad massa, varför en tyngre åkare borde ha fördel (förutsatt att massan sitter på rätt ställe).
/Philip L, 2015-12-08
Svar:
Nej, resonemanget i fråga [869] är korrekt och, tycker jag, tydligt. Du antar att luftmotståndet kan försummas. Det är tvärtom så att luftmotståndet är den dominerande bromsande kraften vid hög hastighet (se länk 1, s 350). Du kan se det vid en störloppstävling. Om en åkare har dålig balans måste hon/han resa sig lite för att återfå balansen. Man ser tydligt på mellantiderna att den sämre aerodynamiken medför att farten minskar.
Det är klart att skidåkarens vikt bara är en parameter som bestämmer resultatet. God teknik och styrka att hålla emot g-krafter (se fråga [15970]) är självklart mycket viktiga -- Lindsey Vonn är relativt stor för en tjej (75 kg, 178 cm lång) men det är säkert den utmärkta tekniken som gör henne så överlägsen! Intressant är också att Anja Pärsson föredragit att vara lättare, med det var för att bli bättre i slalom, se länk 2.
Här är ett annorlunda resonemang som leder till samma slutsats:
Om vi antar att den dominerande bromsande kraften är luftmotståndet kan man härleda ett uttryck för sluthastigheten enligt nedanstående bild från fråga [15385].
Om vi stryker alla konstanter och låter ~ betyda proportionellt mot, så får vi sluthastigheten
Vt ~ sqrt(m/A) ~ sqrt(r3/r2) = sqrt(r)
I termer av massan m får vi eftersom m ~ r3:
Vt ~ sqrt(r) ~ (m1/3)1/2 = m1/6
Sluthastigheten ökar alltså som sjätte roten ur massan.
Se även fråga [18144].
Nej, resonemanget i fråga [869] är korrekt och, tycker jag, tydligt. Du antar att luftmotståndet kan försummas. Det är tvärtom så att luftmotståndet är den dominerande bromsande kraften vid hög hastighet (se länk 1, s 350). Du kan se det vid en störloppstävling. Om en åkare har dålig balans måste hon/han resa sig lite för att återfå balansen. Man ser tydligt på mellantiderna att den sämre aerodynamiken medför att farten minskar.
Det är klart att skidåkarens vikt bara är en parameter som bestämmer resultatet. God teknik och styrka att hålla emot g-krafter (se fråga [15970]) är självklart mycket viktiga -- Lindsey Vonn är relativt stor för en tjej (75 kg, 178 cm lång) men det är säkert den utmärkta tekniken som gör henne så överlägsen! Intressant är också att Anja Pärsson föredragit att vara lättare, med det var för att bli bättre i slalom, se länk 2.
Här är ett annorlunda resonemang som leder till samma slutsats:
Om vi antar att den dominerande bromsande kraften är luftmotståndet kan man härleda ett uttryck för sluthastigheten enligt nedanstående bild från fråga [15385].
Om vi stryker alla konstanter och låter ~ betyda proportionellt mot, så får vi sluthastigheten
Vt ~ sqrt(m/A) ~ sqrt(r3/r2) = sqrt(r)
I termer av massan m får vi eftersom m ~ r3:
Vt ~ sqrt(r) ~ (m1/3)1/2 = m1/6
Sluthastigheten ökar alltså som sjätte roten ur massan.
Se även fråga [18144].

Golfslagets fysik
Fråga:
Hej!
Vi gör vårt gymnasiearbete i fysik och tittar på energiöverföringar i ett golfslag. Mer specifikt undersöker vi själva träffen mellan boll och klubba. Vi har gjort en videoanalys och därigenom fått ut hastigheter för: boll, samt klubba före och efter träff. Vi är dock lite osäkra på hur vi ska räkna med massan för klubban. Ska man göra antagandet att all klubbans massa ligger i klubbhuvudet, eller ska man enbart räkna med klubbhuvudets massa, eller ska man försöka ställa upp en mer avancerad modell? Om inte, hur stort skulle felet tänkas bli, och varför?
Tack på förhand!
Vänliga hälsningar, Emma och Melker
/Melker H, Viktor Rydberg Odenplan, Stockholm 2017-01-09
Hej!
Vi gör vårt gymnasiearbete i fysik och tittar på energiöverföringar i ett golfslag. Mer specifikt undersöker vi själva träffen mellan boll och klubba. Vi har gjort en videoanalys och därigenom fått ut hastigheter för: boll, samt klubba före och efter träff. Vi är dock lite osäkra på hur vi ska räkna med massan för klubban. Ska man göra antagandet att all klubbans massa ligger i klubbhuvudet, eller ska man enbart räkna med klubbhuvudets massa, eller ska man försöka ställa upp en mer avancerad modell? Om inte, hur stort skulle felet tänkas bli, och varför?
Tack på förhand!
Vänliga hälsningar, Emma och Melker
/Melker H, Viktor Rydberg Odenplan, Stockholm 2017-01-09
Svar:
Emma och Melker!
Fysiken bakom golf är mycket komplicerad, men man kan förstå en hel del genom att förenkla problemen. Teorin innehåller ofta fria parametrar som anpassas till mätdata.
I boken The Physics of Golf av Theodore P Jorgensen görs en ganska omfattande analys, men det är inte helt lätt att förstå detaljerna.
Låt oss titta på ert problem som är det enklaste: en central stöt mellan ett klubbhuvud med massan M och en boll med massan m.
Klubbhuvudet har 0 graders loft, så vi har inget spinn. Precis före stöten är klubbhuvudets hastighet V. Efter stöten är klubbhuvudets hastighet u och bollens hastighet är v. Vi antar att stöten är elastisk så att vi inte har några förluster som t.ex. inre friktion pga bollens eller klubbhuvudets deformering. Vid stöten måste vi bevara rörelsemängd och kinetisk energi:
MV = Mu + mv (1)
MV2/2 = Mu2/2 + mv2/2 (2)
Om vi eliminerar u (klubbhuvudets hastighet efter stöten) i (2) med hjälp av (1) får vi för bollens utgånghastighet
v = 2MV/(m+M) = 2V/(m/M + 1) (3)
(I länk 1 finns mer detaljer av härledningen med andra beteckningar.)
Mycket av vad som följer är från kapitel 9 i The Physics of Golf (se ovan).
Om m är mycket mindre än M får vi att v=2V. Detta är alltså den teoretiskt högsta möjliga hastigheten för bollen. Om m=M får vi att v=V (klubbhuvudet är i vila efter stöten). Bollens utgångshastighet är alltså proportionell mot klubbhuvudets hastighet: v = kV. Konstanten k beror av deformationsförluster (se studskoefficient i fråga [20384]) och klubbans loft.
Typiska värden för k är 1.46, 1.30 och 1.12 för driver, järnfemma och järnnia, respektive. Klubbhastigheten för en bra spelare är ungefär 45 m/s vilket ger en bollhastighet med driver av 1.4645=66 m/s. Detta ger en slaglängd på c:a 225 m.
Med ett flexibelt skaft kan man som en hygglig approximation anta att klubbhuvudet vid bollträffen uppför sig som en fri kropp.
Ju större loft en klubba har desto mer spinn får bollen efter träffen. Spinnet ger genom dimplarna och Magnus-effekten en lyftkraft och turbulens som minskar luftmotståndet (se fråga [14113]). Detta gör att bollen flyger längre.
Spinnet kostar emellertid genom att k blir mindre (se ovan). Detta reflekterar faktumet att en del av den överförda energin går till bollens rotationsenergi.
Parentes: Uttrycket v=2V för ett tungt klubbhuvud kan vi få med ett enklare resonemang. Vid en fullständigt elastisk kollision mellan två objekt bevaras den relativa hastigheten. I ovanstående exempel är relativa hastigheten V (klubbhuvudets hastighet). Efter stöten fortsätter klubbhuvudet med hastigheten V och bollen har hastigheten V i förhållande till klubbhuvudet. Bollens hastighet i förhållande till marken är då v=V+V=2V.
Här är fler frågor som behandlar golf:golfboll . Se även länk 2.
/Peter E 2017-01-09
Emma och Melker!
Fysiken bakom golf är mycket komplicerad, men man kan förstå en hel del genom att förenkla problemen. Teorin innehåller ofta fria parametrar som anpassas till mätdata.
I boken The Physics of Golf av Theodore P Jorgensen görs en ganska omfattande analys, men det är inte helt lätt att förstå detaljerna.
Låt oss titta på ert problem som är det enklaste: en central stöt mellan ett klubbhuvud med massan M och en boll med massan m.
Klubbhuvudet har 0 graders loft, så vi har inget spinn. Precis före stöten är klubbhuvudets hastighet V. Efter stöten är klubbhuvudets hastighet u och bollens hastighet är v. Vi antar att stöten är elastisk så att vi inte har några förluster som t.ex. inre friktion pga bollens eller klubbhuvudets deformering. Vid stöten måste vi bevara rörelsemängd och kinetisk energi:
MV = Mu + mv (1)
MV2/2 = Mu2/2 + mv2/2 (2)
Om vi eliminerar u (klubbhuvudets hastighet efter stöten) i (2) med hjälp av (1) får vi för bollens utgånghastighet
v = 2MV/(m+M) = 2V/(m/M + 1) (3)
(I länk 1 finns mer detaljer av härledningen med andra beteckningar.)
Mycket av vad som följer är från kapitel 9 i The Physics of Golf (se ovan).
Om m är mycket mindre än M får vi att v=2V. Detta är alltså den teoretiskt högsta möjliga hastigheten för bollen. Om m=M får vi att v=V (klubbhuvudet är i vila efter stöten). Bollens utgångshastighet är alltså proportionell mot klubbhuvudets hastighet: v = kV. Konstanten k beror av deformationsförluster (se studskoefficient i fråga [20384]) och klubbans loft.
Typiska värden för k är 1.46, 1.30 och 1.12 för driver, järnfemma och järnnia, respektive. Klubbhastigheten för en bra spelare är ungefär 45 m/s vilket ger en bollhastighet med driver av 1.4645=66 m/s. Detta ger en slaglängd på c:a 225 m.
Med ett flexibelt skaft kan man som en hygglig approximation anta att klubbhuvudet vid bollträffen uppför sig som en fri kropp.
Ju större loft en klubba har desto mer spinn får bollen efter träffen. Spinnet ger genom dimplarna och Magnus-effekten en lyftkraft och turbulens som minskar luftmotståndet (se fråga [14113]). Detta gör att bollen flyger längre.
Spinnet kostar emellertid genom att k blir mindre (se ovan). Detta reflekterar faktumet att en del av den överförda energin går till bollens rotationsenergi.
Parentes: Uttrycket v=2V för ett tungt klubbhuvud kan vi få med ett enklare resonemang. Vid en fullständigt elastisk kollision mellan två objekt bevaras den relativa hastigheten. I ovanstående exempel är relativa hastigheten V (klubbhuvudets hastighet). Efter stöten fortsätter klubbhuvudet med hastigheten V och bollen har hastigheten V i förhållande till klubbhuvudet. Bollens hastighet i förhållande till marken är då v=V+V=2V.
Här är fler frågor som behandlar golf:
/Peter E 2017-01-09
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.
Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar

