Enligt huyghens princip kan en vågfront anses vara sammansatt av vågor som sprids cirkulärt åt alla håll. Hur kan då ljuset från en laser hållas samman i en stråle utan att spridas?

Vore tacksam för svar eller dina tankar kring detta.
/Per F

Svar:
Ljus är inte bara en vågrörelse! Det uppför sig som partikel och våg samtidigt! Man får interferens även om man skickar ut enstaka fotoner, så koherensen är irrelevant.

Den raka ljusfronten bevaras i punkter en bit från kanten genom att ljusvågor på ömse sidor tar ut komponenter vinkelrätt mot fortplantningsriktningen, se nedanstående figur. Se vidare fråga 1620 och Huygens'_principle .

Se även fråga 1620

Nyckelord: Huygens princip [3]; dubbelspalt [4];

Ursprunglig fråga:
Jag går just nu tredje året på gymnasiet, och vi håller för tillfället på att arbeta med olika typer av vågrörelser, främst ljus. Ett av de försök vi har gjort går ut på att låta monokromt laserljus passera genom olika typer av spalter (enkelspalt, dubbelspalt, respektive gitter) för att därefter träffa en skärm ett par meter bort. I samtliga fall uppstår som ni säkert känner till ljusfläckar symmetriskt kring centralpunkten på skärmen. I läroboken beskrivs fenomenet så att spaltöppningarna, då de är tillräckligt små, böjer av ljusvågorna, vilka sedan interfererar med varandra varvid utsläckningar (noder) och förstärkningar (bukar) av ljuset uppstår. De drar paralleller till två vattenvågor som interfererar med varandra och även de bildar förstärkningar respektive försvagningar. Emellertid talar de endast om dubbelspalter, respektive gitter. Men, hur applicerar man denna liknelse på försöket med enkelspalten, där man ju bara har en störningskälla för ljuset? Min fysiklärare kunde inte svara på min fråga, så därför vänder jag mig till er och hoppas på ett intressant svar.
/Johan W, Nicolaiskolan, Helsingborg

Svar:
När man ska härleda interferensmönstret i en enkel spalt utgår man från Huygens princip, som säger att varje punkt på en vågfront, utgör en källa till en halvsfärisk våg. Låter man alla dessa vågor interferera med varandra, får man den nya vågfronten. I fallet med enkelspalten, kan man skippa en dimension (den längs spalten), och analysera problemet i två dimensioner. Man delar in spalten i ett stort antal punkter, och låter sfäriska vågor från dessa interferera. Man finner ganska enkelt, att ljuset får maxima i riktningar (vinkel=v) som uppfyller:

sin(v) = nl/d

Ljusets våglängd = l, spaltvidden = d, n = heltal

Man kan även härleda brytningslagen

n₁ sin(i) = n₂ sin(r)

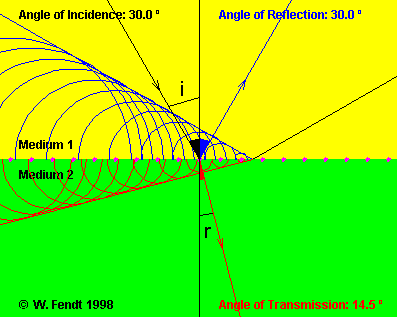
med Huygens princip, se bilden nedan och java-appleten Huygen's Principle and Reflection and Refraction of Waves . Lägg märke till att halvcirklarna är större i det gula mediet (brytningsindex n₁=1) än i det gröna mediet (brytningsindex n₂=2). Detta beror på att ljushastigheten v i ett medium med brytningsindex n ges av v=c/n, dvs ljusets hastighet är större i det gula mediet (c är som vanligt ljushastigheten i vakuum).

Experiment 1: Dra med en vass kniv en skåra i ett papper. Titta genom skåran på en skarp ljuskälla. En gatlykta med en högtrycksnatriumlampa brukar vara bra (gult ljus). Fysiken finns också utanför labbet!

Experiment 2: Behövs: En gatlykta och ett träd eller en buske. Håll för ena ögat och ställ dig så, att en gren precis täcker gatlyktan. Titta nu på smågrenar nära denna punkt. Det lyser på båda sidorna av grenen. Det kan alltså inte vara reflexion (spegling). Det är ljusböjning, som beror på att ljuset är en vågrörelse. På sätt och vis omvändingen till enkelspalten.

Se länk 1 för mer om refraktion. General Physics Java Applets innehåller Java applets för enkel- och dubbelspalt (se under optics).

Nyckelord: Huygens princip [3]; ljusbrytning [23];

1 http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/refr.html

Svar:
Det är lite lättare att resonera om man släpper en stång i vattnet, problemet är ju detsamma.

Experiment med papper, penna, linjal och passare: Dra, med linjalens hjälp, ett 20 mm långt streck på pappret. Ställ in passaren på 5 mm, och rita en massa cirklar med passarspetsen på linjen, längsmed hela linjen. Dra nu med pennan en oval, som markerar ytterkonturen av cirklarna. Sätt nu passarspetsen på ovalen, och dra en massa cirklar runt om hela ovalen. Dra en ny oval utanför den första, och fortsätt med nya cirklar, ny oval, och så vidare. Det är så vågutbredingen går till. Du ser, att ytterkonturerna blir allt rundare, ju längre ut man kommer.

Du har just lärt dig "Huygens princip". Christiaan Huygens var en holländsk fysiker, som levde 1629-1695. Se vidare Huygens'_principle .

 
/KS

Nyckelord: Huygens princip [3];

Ämnesområde	BlandatElektricitet-MagnetismEnergiKraft-RörelseLjud-Ljus-VågorMateriens innersta-Atomer-KärnorPartiklarUniversum-Solen-PlaneternaVärme
Sök efter
Grundskolan eller gymnasiet?	FörskolaGrundskolaGymnasiumLärarutbildning
Nyckelord:	#ljus [63]*astronomi/astrofysik och rymdfart [2]*biologi [20]*fysikaliska definitioner [1]*fysiologi [13]*geologi [16]*idrottsfysik [41]*kemi [13]*meteorologi [17]*miljöpåverkan [14]*nöjesparksfysik [12]*vardagsfysik [62]*verktyg [8]3d-bilder [6]aberration [1]absoluta nollpunkten [9]acceleration [6]accelerator [7]addition av hastigheter [1]aerosol [3]akustik [6]alfasönderfall [6]annihilation [14]antimateria [16]arbete [23]Arkimedes princip [27]asteroid [10]astrobiologi [9]astrologi [5]atomradie [8]Avogadros tal [3]ballong [17]bandgenerator [3]barometerformeln [1]batteri [25]belysning [6]bernoullieffekten [6]betasönderfall [14]big bang [34]bildskärmar [4]bindningsenergi [23]blixt [17]blå himmel [12]bobåkning/störtlopp [4]Bohrs atommodell [9]Bose-Einstein-kondensat [6]brandvarnare [2]bränslecell [3]centrifugalkraft [15]centripetalkraft [11]comptonspridning [3]corioliskraft [6]dagens längd [3]daggpunkten [2]dagjämning [6]Darwins evolutionsteori [8]de Broglie våglängd [1]decibel [9]diffraktion [4]diffusion [1]dimkammare [2]dopplereffekt (ljud) [2]dopplereffekt (ljus) [1]drickande fågeln [1]dubbelspalt [4]duschdraperi [2]Einstein, Albert [1]elasticitet [4]elastisk stöt [11]elektrisk krets [7]elektrisk ström, hastighet [4]elektrisk ström, skada [6]elektromagnetisk strålning [16]elektronskal [11]elsäkerhet [18]energikällor [25]energilagringssystem [7]enkelspalt [1]entropi [7]EPR, Bell, Aspect [3]evighetsmaskin [13]exoplaneter [13]fallrörelse [21]faradaybur [10]fasdiagram [7]felberäkning [5]Fermats princip [1]ferromagnetism [4]fiberoptik [4]fission [15]fluorescens [6]flygplansvinge [8]flykthastighet [4]formel 1 [2]forskningskarriär [1]fossila bränslen [13]fotoelektrisk effekt [7]friktion [48]friktionskoefficient [5]frågelådan [12]Fukushima [5]fusion [15]fysik [10]fysik, förståelse av [16]fysik, historia [1]fysik, nytta med [6]fysikalisk modell [11]färg/färgseende [32]färgkraften [8]Gaia [3]galax [25]gamma ray burst [2]gaslagen, allmänna [22]genomskinlighet [18]genteknik [2]geodesi/gravimetri [2]geostationär satellit [7]gitter [5]g-krafter [16]glasögon [2]gluoner [6]glödlampa [18]gnistkammare [1]golfboll [13]GPS [3]gravitation [3]gravitationslins [5]gravitationsvågor [12]gravity assist [2]gregorianska kalendern [1]grundämnen, bildandet av [5]grundämnen, förekomst [4]gunga [4]gyroskop [1]halofenomen [2]halogenlampa [3]halveringstid/sönderfallskonstant [4]harmonisk svängning [4]Heisenbergs obestämdhetsrelation [11]helikopter [4]higgspartikeln [9]Hiroshima/Nagasaki [4]hologram [5]HR-diagram [2]Huygens princip [3]hyperfinstruktur [1]hägring [3]hävstång [5]hörsel [10]Illustrerad Vetenskap [17]impedans [3]induktans [6]induktion [13]inertialsystem [6]inflation [5]infraljud [7]interferens [12]Internationella rymdstationen [5]iskristaller [5]istider [7]joniserande strålning [4]jordens atmosfär [9]jordens inre [11]jordens magnetfält [21]jordens rotation [20]kall fusion [7]kaos [3]kapillärkraft [10]kastparabel [8]Keplers lagar [13]Kirchhoffs strålningslag [4]klimat [9]knäppande aluminiumfolie [2]kokande vatten [15]kokpunkts/fryspunkts förändring [10]kol [3]kol-14 metoden [4]koldioxidcykeln [6]kollisionssäkerhet [1]komet [12]kosmisk bakgrundsstrålning [14]kosmisk strålning [3]kosmologi [24]kraft [12]kraftledning [7]kraftverkningar [9]kursplan [3]kvantmekanik [27]kvark [12]kvasar [3]kylning [6]kärndata [3]kärnenergi [18]kärnfysik [2]kärnkrafter [7]kärnkraftsavfall [11]kärnreaktion [5]kärnvapen [15]Lagrange-punkt [2]latitud/longitud [1]lins [11]liv i universum [9]livets uppkomst [1]ljud [5]ljud, interferens [6]ljud, resonans [14]ljudbang [3]ljudhastigheten [19]ljusbrytning [23]ljushastigheten [20]ljusreflektion [16]lorentztransformation [2]luftmotstånd [10]lufttryck [19]luminiscens [5]lutande plan [14]lysdiod [12]lysrör [9]lågenergilampa [13]längdkontraktion [5]magnetisk monopol [4]magnetism [48]magnetron [1]Mars [11]massa, trög/tung [4]massa-energi [1]massa-kraft [1]massbestämning [2]mass-luminositetsrelation [2]matematik i fysik [6]matematik, skriva [2]materia [6]Maxwells ekvationer [3]metabolism [3]metall, smältpunkt [2]meteorit [17]mikrovågsugn [23]Milankovitch cykler [2]mobiltelefon, strålning från [4]monstervåg [4]Monte Carlo-metoder [1]Mpemba-effekten [2]MRI [5]musikinstrument [17]månens bana [13]månens synbara storlek [1]månfärder [7]mörk energi [6]mörk materia [17]nanoteknik [6]Nationalencyklopedin [1]naturkonstant [5]naturlig radioaktivitet [3]NEO [9]neutrino [16]neutron [4]neutronstjärna [9]Newtons gravitationslag [12]Newtons rörelselagar [21]Newtons vagga [2]norrsken [7]nova [1]nyheter [11]Olbers paradox [2]osmos [8]parallaxmetoden [4]parapsykologi [6]parbildning [7]Pascals lag [5]pauliprincipen [10]pendel, konisk [2]pendel, plan [8]PET [1]Plancks strålningslag [6]planet [14]planeters atmosfär [2]planeters form [3]plastfolie [1]polarisation [7]polaroidglasögon [3]potential/potentiell energi [26]prisma [1]projektarbete [1]pseudovetenskap [9]radioaktiv datering [7]radioaktivitet, sönderfallskedja [7]radioaktivt sönderfall [34]radioteleskop [1]radon [4]raketekvationen [2]raketmotor [8]regn [1]regnbåge [5]relativistiskt massberoende [3]relativitetsteorin, allmänna [29]relativitetsteorin, speciella [40]religion [3]resistans [12]resistansförluster [2]resonans [4]richterskalan [2]ringklocka [4]rymddräkt [5]rymdfärder [23]rödförskjutning [5]röntgenrör [3]rörelseenergi [12]rörelsemängd [14]rörelsemängdsmoment [12]satellitbana [12]Saturnus´ ringar [5]schrödingerekvationen [4]Schrödingers katt [2]science fiction [6]segling [5]serie- och parallellkoppling [14]SETI [1]shareware [1]SI-enheter [4]skruvad boll [9]skymning [1]slumptal [1]SN 1987A [4]solaktivitet [2]solarkonstanten [6]solcell [6]solen [2]solen, avstånd till [1]solenergi [14]solens energiproduktion [9]solens utveckling [4]solförmörkelse [3]solsystemet [7]solsystemet, avstånd och rörelse [3]solsystemets bildande [11]specifik värmekapacitet [21]spegel [10]spektrum [11]standardmodellen [23]statisk elektricitet [9]stearinljuslåga [14]stjärna [3]stjärnhimlen [12]stjärnors utveckling [15]stroboskopeffekt [2]strålning, faror med [24]strålning, in-/ut- [6]strängteori [7]strömning [1]supernova [13]supertunga grundämnen [1]supraledning [7]svart hål [39]synvilla [5]sönderfallskonstant [3]teleskop [10]temperatur/temperaturskalor [15]temperaturstrålning [22]termodynamik [16]termometer [7]termos [3]Three Mile Island [2]tid [9]tidsdilatation [6]tidsekvation [4]tidvatten [12]tjerenkovstrålning [2]Tjernobyl [11]totalreflektion [7]transformator [6]transmutation av kärnavfall [2]trefas [3]trippelpunkt [2]tröghetsmoment [8]tsunami [5]tunneleffekt [3]TV [9]tvillingparadoxen [5]tyngdaccelerationen [12]tyngdlöshet [12]ultraljud [8]universums expansion [15]uppvärmning av bostäder [2]utvidgning [6]UV-ljus [11]vakuum [7]vatten/is [34]vattenkraft [7]vattenpump [2]Venus [10]verkningsgrad [21]vetenskaplig metod [18]Wikipedia [4]WIMPs [3]vindavkylning [3]vindenergi [9]Vintergatan [6]vridmoment [7]vulkanism [5]våg/partikelegenskaper [7]vågenergi [3]vågfunktion [2]värmemängd [3]värmepump/kylskåp [6]värmeöverföring/transport [39]väteatomen [2]vätskedroppsmodellen [5]växthuseffekten [31]ytspänning [18]årstider [4]ögat [16] (Enda villkor)
Definition:	absoluta nollpunktenabsorptionsspektraaccelerationackommodationackretionsskivaadiabatisk processaggregationstillståndakustisk impedansallmänna gaslagenampereamperetimmeannihilationantimateriaarbetearkimedes principasteroidastigmatismastrobiologiastronomisk enhetatommassaatomnummeravogadros talbandspektrabatteribenhams snurrabergvärmebernoullis ekvationbetasönderfallbig bangbindningsenergibindningsenergibioluminiscensboltzmanns konstantbrewstervinkelnbrytningsindexbrännpunktbubbelkammarecarnotprocesscentrifugalkraftcentripetalkraftcitronbattericorioliskraftendarwins evolutionsteoride broglie våglängdendecibeldeltondensitetdielektrisk polarisationdiffus reflektiondiffusiondimensiondioptridiskret spektrumdispersiondopplereffektdotternukliddulong-petits lage=mc2ekvivalensprincipenelasticitetelastisk energieldelektrisk dipolelektrisk laddningelektrisk spänningelektrisk strömelektriska fältstyrkanelektroluminiscenselektromagnetisk strålningelektroninfångningelektronskalemissionsnebulosaemissionsspektraemsendoterm reaktionenergienergikällaenergiomvandlingenergipincipenenergipotentialentropi (makroskopisk definition)entropi (mikroskopisk definition)evighetsmaskinexciterade tillståndexoplanetexoterm reaktionextremofilerfallrörelsefaradays burfasdiagramfermats principferminivånfissionfluidfluorescensflygplansvingeflykthastighetenfokalpunktfokusfosforescensfossila bränslenfotokromismfotomotståndfotonfotosfärenfotosyntesfouriers lagfraktalfranck-hertz försökfriktionfriktionskoefficientfritt fallfundamentala naturkrafternafusionfysikfysikaliska modellerfysiologifärgblindhetfärgseendefönybara bränslenförnybara energikällorgaiagalaxgammastrålninggaskonstantengeneratorgeostationär satellitgeotermisk energiglobal uppvärmninggluonerglödlampagravitationgravitationengravitationskonstantengravitationsvågorgrundläggande fysikgrundtillståndetgrundtongrundämnegrå starrgula fläckenhalleffekthalogenlampahalveringstidhastighethawkingstrålninghertzsprung-russell diagramhiggspartikelnhookes laghornhinnanhubble ultra deep fieldhuygens principhändelsehorisontenhästkrafthävstångicke-joniserande strålningideal gasimpedansinduktansinduktioninertialsysteminflationinfraljudinklinationinre konversioninre resistansinterferensinverterad populationisomerisospinnisoterm processisotoperjondriftjoniserande strålningjordfelsbrytarekalibreringkall fusionkalorikapacitanskapillärkraftenkastparabelkedjereaktionkemisk bindningkemisk bindningkemisk reaktionkemoluminiscenskeplers andra lagkeplers första lagkeplers tredje lagkilogramkirchhoffs lagkirchhoffs strålningslagkiselklassisk fysikklorofyllkokarreaktorkokpunktkolkornsmikrofonkometkomplementfärgkonservativ kraftkontinuerligt spektrumkonvektionkoronankorrespondesprincipenkosmiska bakgrundsstrålningenkosmologikosmologiska rödskiftetkosmologiska standarmodellenkraftkristallkritisk densitetkritisk massakromosfärenkuiperbältetkundts rörkvantdatorkvantmekanikkvantmekanisk sammanflätningkvarkkvark-gluon plasmakvartskvasarkvasipartiklarkärnkrafterkärnreaktionkärnreaktorerkärnvapenlagrange-punkternalaserlenz lagleptonlila linjespektralivljudljusljusabsorptionljusbrytningljushastighetenljuskällorljusutbyteljusårluftmotståndluminiscenslutande planlysdiodlysrörlågenergilampalägesenergilängdkontraktionmachomagnetismmagnuseffektenmarkradarmarkvärmemaskhålmassamasscentrummassdefektmassenhetmassexcessmasstalmateriamaxwell–boltzmannfördelningenmaxwells ekvationermedelvärdetmegaton tntmeissnereffektenmerkurius periheliumprecessionmetafysikmetallbindningmetalldetektormetallicitetmeteormeteoritmeteoroidmilankovitch cyklermodern fysikmodernuklidmolmolekylmymetallmånemätfelmörk energimörk materiamörk nebulosamössbauer-effektennanometertekniknanopartikelnanotekniknationalencyklopedinnaturvetenskapnavigeringneoneutrinoneutrinooscillationerneutroninducerad fissionneutronstjärnanewtonnewtons andra lagnewtons avsvalningslagnewtons första lag (tröghetslagen)newtons gravitationslagnewtons tredje lagnobelpris i fysik 1925nobelpris i fysik 1993nobelpris i fysik 2015nobelpris i fysik 2017normalkraftennorrskennuklidnuklidkartanutida fysiknärsynthetockhams rakknivohms lagoorts kometmolnoregelbunden galaxosmosparapsykologiparbildningpascals princippauliprincipenperiodiska systemetplanck timeplancks strålningslagplanetplasmaplasmaplasmaplasticitetpn-övergångpolarisationpolspänningpolär jetstrålepotentialproton-protonkedjanpseudovetenskapqcdqedradiative forcingradioaktivitetradioluminiscensraketekvationenrayleigh-spridningreaktansreflektionrefraktionrelativ luftfuktighetrelativistisk energirelativistisk jetresistansresistivitetresistivitetresonansrussells tekannarörelseenergirörelsemängdrörelsemängdsmomentschwarzschildradiensekulär jämviktsekundsfärisk aberrationsingularitetsi-prefixsjälvinduktansskottsekundslumpvisa mätfelsnells lagsolarkonstantensolcellersolenergisolens centrumsolförmörkelsesolkraftverksolvärmespallationspecifik värmekapacitetspektroskopispektrumspinnspontan fissionstandardavvikelsenstandardmodellenstatisk elektricitetstefan–boltzmanns lagstimulerad emissionstjärnastjärnbildstrålningstrålningstråloptiksträngteorinstående vågstämgaffelsupermassiva svarta hålsupernovasupertungt grundämnesuprafluiditetsupraledningsvart hålsvänghjulsystematiska mätfelsåpbubblasäkringsönderfallskedjasönderfallskonstantentemperaturtemperaturspektrumtermodynamiktermodynamikens andra huvudsatstermodynamikens första huvudsatstidtidsdilatationtidsekvationentidvattentidvattenkraftertillämpad fysiktjerenkovstrålningtotalreflektiontransformatortransparenstrippelpunktentrycktryckvattenreaktortröga massantröghettunga massantvillingparadoxentyngdtyngdlöshettyngdpunktentyp ii supernovaufoultraljudultraviolett strålningultraviolettkatastrofenunderkylningvakuumvakuumfluktuationervakuumpolarisationvalenselektronvattenburen värmevattenkraftvattenkraftvektorerverkningsgradvetenskaplig metodwiens förskjutningslagwikipediaviktwimpvindkraftvintergatanvintergatanvirtuell bildvit dvärgvoltvridmomentv-t diagramvåglängdenvåg-partikeldualitetvågtalvärmeledningvärmemängdvärmepumpvärmeöverföringvätelika jonervätskedroppsmodellenväxthuseffektenytenergiångbildningsvärmeångtryckårstidernaädelgasädelgaserögats linsöratöversynthetövertoner (Enda villkor)

---

Om du inte hittar svaret i databasen eller i

Sök i svenska Wikipedia:

Sök i Nationalencyklopedin

   

Sök med Google

   

- fråga gärna här.