Vill du ha ett snabbt svar - sök i databasen
Nyckelord: 3d-bilder
5 träffar
Hur fungerar 3D-bilder som är uppbyggda av punkter?
Fråga:
Jag har en liten fråga angående 3D-bilder (som de som fanns i Aftonbladet/Expressen).
Hur fungerar dem, vilken är vetenskapen som ligger bakom detta spännande synfenomen?
/Simon O, Duveholmsskolan, Katrineholm 1998-11-10
Jag har en liten fråga angående 3D-bilder (som de som fanns i Aftonbladet/Expressen).
Hur fungerar dem, vilken är vetenskapen som ligger bakom detta spännande synfenomen?
/Simon O, Duveholmsskolan, Katrineholm 1998-11-10
Svar:
Vi har inte sett de bilder du sett, antagligen är det ett geometriskt
mönster, som man ska betrakta på ett visst sätt. Plötsligt växer en
tredje dimension fram. Det är inte lätt att förklara, det är mycket
arbete nedlagt på de bilderna.
Du kan själv göra en del enkla försök, som illustrerar det grundläggande fenomenet, se nedanstående figur. Ta ett vitt papper och rita 2 punkter
på 4 cm avstånd. Gör dom 2 mm stora. 11 mm till vänster om den
vänstra punkten ritar du en liten punkt, och 10 mm till
vänster om den högra punkten ritar du en liten punkt.
Lägg märke till skillnaden i avstånden, den är viktig.
Nu ska man "slötitta" på punkterna, och försöka att få dom
att gå ihop. I själva verket ser man då 3 st 2 mm punkter,
men det är bara mittbilden som är intressant. Ligger den lilla punkten framför eller bakom? Förklaring? Testa det
på dina kompisar!
Håll för ett öga och håll huvudet stilla. Titta sen med båda
ögonen. Skillnad?
Den bild vi upplever är inte den som faller på näthinnan. Hjärnan har gjort åtskilligt med bildinformationen. Det här är fantastiskt spännande!
Det enkla exemplet nedan, överst är ganska lätt att förstå: vänstra ögat ser avståndet mellan den mindre och den större punkten lite större än vad det högra gör. Hjärnan tolkar detta som att den mindre punkten ligger närmare än den större. Wikipedia-artikeln Autostereogram innehåller en samling mer komplicerade 3D-bilder som bygger på samma princip, se ett exempel underst nedan.
innehåller en samling mer komplicerade 3D-bilder som bygger på samma princip, se ett exempel underst nedan.
Vi har inte sett de bilder du sett, antagligen är det ett geometriskt
mönster, som man ska betrakta på ett visst sätt. Plötsligt växer en
tredje dimension fram. Det är inte lätt att förklara, det är mycket
arbete nedlagt på de bilderna.
Du kan själv göra en del enkla försök, som illustrerar det grundläggande fenomenet, se nedanstående figur. Ta ett vitt papper och rita 2 punkter
på 4 cm avstånd. Gör dom 2 mm stora. 11 mm till vänster om den
vänstra punkten ritar du en liten punkt, och 10 mm till
vänster om den högra punkten ritar du en liten punkt.
Lägg märke till skillnaden i avstånden, den är viktig.
Nu ska man "slötitta" på punkterna, och försöka att få dom
att gå ihop. I själva verket ser man då 3 st 2 mm punkter,
men det är bara mittbilden som är intressant. Ligger den lilla punkten framför eller bakom? Förklaring? Testa det
på dina kompisar!
Håll för ett öga och håll huvudet stilla. Titta sen med båda
ögonen. Skillnad?
Den bild vi upplever är inte den som faller på näthinnan. Hjärnan har gjort åtskilligt med bildinformationen. Det här är fantastiskt spännande!
Det enkla exemplet nedan, överst är ganska lätt att förstå: vänstra ögat ser avståndet mellan den mindre och den större punkten lite större än vad det högra gör. Hjärnan tolkar detta som att den mindre punkten ligger närmare än den större. Wikipedia-artikeln Autostereogram
 innehåller en samling mer komplicerade 3D-bilder som bygger på samma princip, se ett exempel underst nedan.
innehåller en samling mer komplicerade 3D-bilder som bygger på samma princip, se ett exempel underst nedan.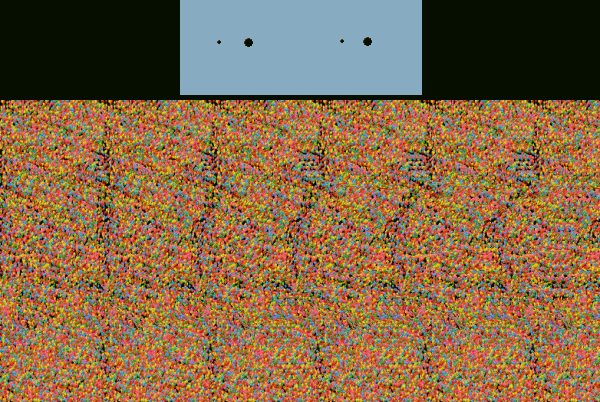
Fråga:
Hur fungerar 3D-Glasögon när man tittar på en 3D-bild och
varför blir det så att bilden kommer ut jag vill ha reda på det snarast.
/Fredrik L, sotenäs skolan, Kungshamn 2000-05-18
Hur fungerar 3D-Glasögon när man tittar på en 3D-bild och
varför blir det så att bilden kommer ut jag vill ha reda på det snarast.
/Fredrik L, sotenäs skolan, Kungshamn 2000-05-18
Svar:
Det finns flera olika principer, men det vanligaste är att man har två bilder
tryckta över varandra, den ena i rött och den andra i blått. Så tittar man med
glasögon med röd och blåfilter. Genom det röda filtret ser man den blå
bilden, genom det blå filtret ser man den röda bilden. OBS! Vi har inte
skrivit fel!
Experiment: Skriv med en rödpenna och titta på texten genom ett rödfilter
och ett blåfilter.
/KS 2000-06-07
Det finns flera olika principer, men det vanligaste är att man har två bilder
tryckta över varandra, den ena i rött och den andra i blått. Så tittar man med
glasögon med röd och blåfilter. Genom det röda filtret ser man den blå
bilden, genom det blå filtret ser man den röda bilden. OBS! Vi har inte
skrivit fel!
Experiment: Skriv med en rödpenna och titta på texten genom ett rödfilter
och ett blåfilter.
/KS 2000-06-07
Jag undrar hur tredimensionella bilder med 3d-glasögon fungerar
Fråga:
Jag undrar hur tredimensionella bilder med 3d-glasögon fungerar, gärna ingående.
/Marie W, svalöfsgymnasium, Svalöv 2004-12-11
Jag undrar hur tredimensionella bilder med 3d-glasögon fungerar, gärna ingående.
/Marie W, svalöfsgymnasium, Svalöv 2004-12-11
Svar:
Anledningen till att vi kan se tredimensionellt är att vi har två ögon på ett litet avstånd från varandra. Ögonen ser omgivningen från lite olika riktning, och de resulterande något olika bilderna tolkas av hjärnan. För föremål som ligger nära är detta hur vi kan bedöma avstånd. För föremål längre bort använder vi i stället kunskapen om hur stora föremål är i verkligheten, se länk 1.
Det traditionella sättet att åstadkomma 3D-effekt är att kombinera de två något olika bilderna på så sätt att den ena görs röd och den andra blå. Om man betraktar denna kombinerade bild genom glasögon med ett rödfilter på ena sidan och ett blåfilter på den andra, får man en tredimensionell effekt. Nackdelen är att bilden blir svartvit (hjärnan ser till att korrigera för det extra blå och röda).
Numera finns även färgfilm i 3D (t.ex. IMAX). För detta använder man i stället polarisationsglasögon och projicerar de olika bilderna med olika cirkulär polarisation.
Länk 2 nedan (på engelska) ger en ganska ingående förklaring av 3D-bilder.
En mycket gammal metod att gör 3D-bilder är att helt enkelt lägga de två bilderna bredvid varandra. Detta fungerar dock inte särskilt bra eftersom man måste skela med ögonen för att se en 3D-effekt. Det är mycket varierande hur bra olika människor klarar av detta. Bilden nedan till vänster är egenligen avsedd att betraktas med stereo-glasögon, men man (nåja, somliga med lite övning) får relativt bra effekt med "skelmetoden".
Bildtexten (bilderna är av en del av marsytan från ESA) säger: Hecates Tholus volcano as seen by the High Resolution Stereo Camera (HRSC) on Mars Express during orbit 32 from an altitude of 275 km. The 3D image on the left requires stereoscopic (red/green) glasses to view.
Anledningen till att vi kan se tredimensionellt är att vi har två ögon på ett litet avstånd från varandra. Ögonen ser omgivningen från lite olika riktning, och de resulterande något olika bilderna tolkas av hjärnan. För föremål som ligger nära är detta hur vi kan bedöma avstånd. För föremål längre bort använder vi i stället kunskapen om hur stora föremål är i verkligheten, se länk 1.
Det traditionella sättet att åstadkomma 3D-effekt är att kombinera de två något olika bilderna på så sätt att den ena görs röd och den andra blå. Om man betraktar denna kombinerade bild genom glasögon med ett rödfilter på ena sidan och ett blåfilter på den andra, får man en tredimensionell effekt. Nackdelen är att bilden blir svartvit (hjärnan ser till att korrigera för det extra blå och röda).
Numera finns även färgfilm i 3D (t.ex. IMAX). För detta använder man i stället polarisationsglasögon och projicerar de olika bilderna med olika cirkulär polarisation.
Länk 2 nedan (på engelska) ger en ganska ingående förklaring av 3D-bilder.
En mycket gammal metod att gör 3D-bilder är att helt enkelt lägga de två bilderna bredvid varandra. Detta fungerar dock inte särskilt bra eftersom man måste skela med ögonen för att se en 3D-effekt. Det är mycket varierande hur bra olika människor klarar av detta. Bilden nedan till vänster är egenligen avsedd att betraktas med stereo-glasögon, men man (nåja, somliga med lite övning) får relativt bra effekt med "skelmetoden".
Bildtexten (bilderna är av en del av marsytan från ESA) säger: Hecates Tholus volcano as seen by the High Resolution Stereo Camera (HRSC) on Mars Express during orbit 32 from an altitude of 275 km. The 3D image on the left requires stereoscopic (red/green) glasses to view.

Osäkra avstånd till stjärnor
Fråga:
Mina elever håller på med en labb där de ska placera ut karlavagnens stjärnor med rätt inbördes avstånd. Problemet är avstånden till jorden. De är helt olika beroende på vilken bok/nätkälla man än tittar i. Detta gör labben helt meningslös. Vilka avstånd är de rätta?
Här följer ytterligheterna vi har hittat:
Alkaid (Benetnash) 100 - 210 ly
Mizar (Alioth) 60 - 78,2 ly
Alioth 70 - 80,9 ly
Megrez 65 - 81,4 ly
Phekda 78,2 - 90 ly
Merak 75 - 80 ly
Dubhe 94,5 - 124 ly
/Tomas P, Stavby, Stavby 2005-01-13
Mina elever håller på med en labb där de ska placera ut karlavagnens stjärnor med rätt inbördes avstånd. Problemet är avstånden till jorden. De är helt olika beroende på vilken bok/nätkälla man än tittar i. Detta gör labben helt meningslös. Vilka avstånd är de rätta?
Här följer ytterligheterna vi har hittat:
Alkaid (Benetnash) 100 - 210 ly
Mizar (Alioth) 60 - 78,2 ly
Alioth 70 - 80,9 ly
Megrez 65 - 81,4 ly
Phekda 78,2 - 90 ly
Merak 75 - 80 ly
Dubhe 94,5 - 124 ly
/Tomas P, Stavby, Stavby 2005-01-13
Svar:
Tomas! Du har stött på ett problem som är typiskt för fysikaliska mätningar: de är behäftade med osäkerheter. Man skall aldrig bara ge ett värde på en storhet - man måste även ge en uppskattning av osäkerheten.
Var gäller data för stjärnor i UMa (Ursa Major, Karlavagnen är en del av denna) finns några av stjärnorna i The brightest stars . Mer komplett är The Bright Star Catalogue
. Mer komplett är The Bright Star Catalogue (länk 1), där alla stjärnorna du nämner finns.
(länk 1), där alla stjärnorna du nämner finns.
Låt oss ta Mizar som exempel. Enligt Sky2000-katalogen i The Bright Star Catalogue är parallaxen 0.047+/-0.005 bågsekunder. Avståndet i ljusår är 3.26/parallax, så avståndet blir 69+/-8 ljusår, vilket inte stämmer så illa med dina uppgifter. Jag kan inte se var mätningarna kommer ifrån, men osäkerheten 0.005 bågsekunder är rimligt för en klassisk mätning med markbaserade teleskop.
är parallaxen 0.047+/-0.005 bågsekunder. Avståndet i ljusår är 3.26/parallax, så avståndet blir 69+/-8 ljusår, vilket inte stämmer så illa med dina uppgifter. Jag kan inte se var mätningarna kommer ifrån, men osäkerheten 0.005 bågsekunder är rimligt för en klassisk mätning med markbaserade teleskop.
Jag föreslår ni använder SKY2000 data, länk 1. Klicka på HR beteckningen i första kolumnen och välj SKY2000 Master Star Catalog. Avståndet räknar ni alltså ut som 3.26/parallax. Den relativa osäkerheten i exemplet Mizar blir 0.005/0.047=0.11. Osäkerheten i avståndet blir då 0.1169=8.
I dag kan man emellertid göra mycket bättre mätningar med rymdbaserade teleskop. Det finns t.ex. 'Hipparcos and Tycho Catalogues', med mycket mer exakta data. De är emellertid hopplöst svåra att använda för en amatör. Programmet Stellarium innehåller emellertid Hipparcos-data mycket lättillgängligt. För mer om parallax, se
innehåller emellertid Hipparcos-data mycket lättillgängligt. För mer om parallax, se parallaxmetoden .
Under länk 2 finns ett par 3D-bilder av Karlavagnen och Orion som är framställda från data från satelliten Hipparcos. Bilden på Karlavagnen är reproducerad i mindre skala nedan. Om man betraktar bilderna med klassiska röd-gröna 3D-glasögon (röda filtret på vänster öga) ser man tydligt att stjärnorna ligger på mycket olika avstånd. Tack professor Lennart Lindegren, Institutionen för astronomi, Lund som är en medarbetare i Hipparcos-projektet för att vi får publicera bilderna! För mer om Hipparcos-projektet och det framtida Gaia-projektet, se Astrometri .
.
Tomas! Du har stött på ett problem som är typiskt för fysikaliska mätningar: de är behäftade med osäkerheter. Man skall aldrig bara ge ett värde på en storhet - man måste även ge en uppskattning av osäkerheten.
Var gäller data för stjärnor i UMa (Ursa Major, Karlavagnen är en del av denna) finns några av stjärnorna i The brightest stars
Låt oss ta Mizar som exempel. Enligt Sky2000-katalogen i The Bright Star Catalogue
Jag föreslår ni använder SKY2000 data, länk 1. Klicka på HR beteckningen i första kolumnen och välj SKY2000 Master Star Catalog. Avståndet räknar ni alltså ut som 3.26/parallax. Den relativa osäkerheten i exemplet Mizar blir 0.005/0.047=0.11. Osäkerheten i avståndet blir då 0.1169=8.
I dag kan man emellertid göra mycket bättre mätningar med rymdbaserade teleskop. Det finns t.ex. 'Hipparcos and Tycho Catalogues', med mycket mer exakta data. De är emellertid hopplöst svåra att använda för en amatör. Programmet Stellarium
Under länk 2 finns ett par 3D-bilder av Karlavagnen och Orion som är framställda från data från satelliten Hipparcos. Bilden på Karlavagnen är reproducerad i mindre skala nedan. Om man betraktar bilderna med klassiska röd-gröna 3D-glasögon (röda filtret på vänster öga) ser man tydligt att stjärnorna ligger på mycket olika avstånd. Tack professor Lennart Lindegren, Institutionen för astronomi, Lund som är en medarbetare i Hipparcos-projektet för att vi får publicera bilderna! För mer om Hipparcos-projektet och det framtida Gaia-projektet, se Astrometri

Hur fungerar en Mirage?
Fråga:
Hur går strålgångarna i en dubbelkonkav spegling?
På MacDonalds fanns en leksak med två motvarandra konkava speglar som lyfte upp en bild av leksaken som finns inuti. Jag vet hur strålningen i en konkav spegel går men har inte lyckats rita hur det fungerar här. Varför blir bilden upplyft ovanför spegeln?
/Gunni L, Stenkulaskolan, Malmö 2009-12-05
Hur går strålgångarna i en dubbelkonkav spegling?
På MacDonalds fanns en leksak med två motvarandra konkava speglar som lyfte upp en bild av leksaken som finns inuti. Jag vet hur strålningen i en konkav spegel går men har inte lyckats rita hur det fungerar här. Varför blir bilden upplyft ovanför spegeln?
/Gunni L, Stenkulaskolan, Malmö 2009-12-05
Svar:
Efter lite problem att identifiera spegelsystemet (tack Carina och Thomas!) har jag slutligen hittat tillräckligt bra dokumentation för att kunna beskriva hur det fungerar. Spegelsystemet heter heter 'Mirage® 3D Hologram Maker' eller 'Mirascope'. De flesta sajter man hittar med en Google-sökning är bara försäljning av Miragen och ingen förklaring. Länk 1 var emellertid bättre med en ganska detaljerad beskrivning. Där fanns även en YouTube-video som visar hur det ser ut (klicka på högerpilen för att starta):
Här är en demo för en skolklass som en del av en optiklektion. Videon visar bland annat hur man kan belysa den reella bilden med en ficklampa:
Lite mer sökande gav länk 2, som verkligen beskriver hur det fungerar. Bilderna nedan kommer från denna sida.
För det första så är det inte ett riktigt hologram - det ser bara ut som ett hologram. Ett hologram bygger på interferens med (normalt) en laserstråle. Denna konstruktion innehåller bara två paraboliska konkava speglar vända mot varandra.
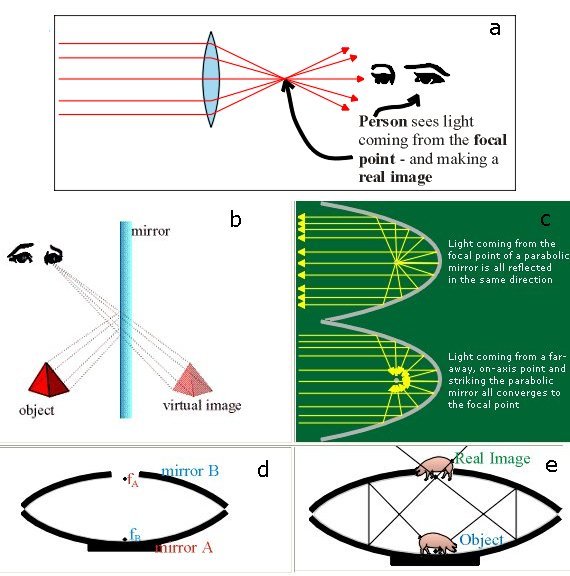
Låt oss börja med att diskutera reella och virtuella bilder. Om man riktar ett vanligt teleskop med en positiv lins mot ett föremål (figur a nedan) och tittar på fokalplanet från sidan så ser man ingenting eftersom synfältet i kikaren är mycket begränsat. Den reella bilden i fokalplanet kan endast betraktas från en riktning rakt motsatt riktningen mot objektivet. Detta är var okularet normalt finns.
En vanlig spegel (figur b) ger en bild belägen bakom spegeln dit inga ljusstrålar når. Detta kallas för en virtuell bild. Bilden ser ut att komma från bakom spegeln, men där finns (eftersom det inte finns några ljusstrålar där) inget som kan fångas upp på en skärm.
Figur c visar hur en parabolisk spegel fungerar. Ljus från fokalpunkten kommer att gå ut som ett parallellt knippe i optiska axelns (parabelns storaxel, spegelns symmetriaxel) riktning. Omvänt så kommer ljus som infaller parallellt med optiska axeln (från ett avlägset föremål) att samlas i fokalpunkten.
Figur d visar hur Mirage är konstruerad. Den nedre spegeln (A) har sitt fokus nära den övre spegelns (Bs) plan. Fokus för B ligger på samma sätt i As plan.
Man kan nu förstå strålgången i figur e. En stråle från t.ex. knorren kommer ju nästan från fokalpunken för spegel B, och kommer alltså att speglas så att den kommer parallellt med optiska axeln. Den kommer sedan att speglas av spegel A mot dess fokus. Ljusstrålar i olika riktningar kommer att bygga upp en fullständig reell bild av föremålet nära fA. Det ser alltså ut som om grisen är i punkten fA och inte i punkten fB. Enda skillnaden är att den avbildade grisen är roterad 180 grader i horisontalplanet.
Observera att föremålet i fB är skymt av spegeln B eftersom man tittar från sidan. Uppifrån ser man ingen bild, men man ser föremålet.
Varför ser man bilden från sidan i Mirage men inte i fallet med den positiva linsen i figur a? I fallet Mirage är synfältet mycket stort, så bilden blir till en fullständig en 3d-kopia av objektet som kan betraktas från alla riktningar. För den positiva linsen är synfältet som sagt mycket begränsat, så det finns inga ljusstrålar som går ut åt sidorna.
Hur var det med belysningen av bilden i den andra videon? Även en reell bild på den lilla grisen är, som man märker om man petar på den, immateriell. Hur kan den då reflektera ljus från ficklampan? Det kan den naturligtvis inte, utan det är så att ljuset från lampan går samma men omvända vägen som ljuset från föremålet. Det är alltså föremålet som belyses, men via två reflektioner i först den nedre och sedan den övre spegeln.
Mirage-principen är inte bara en kul grej, utan konstruktionen används som aberationskorrigerare i teleskop och kallas då av uppenbar anledning 'clam-shell corrector'. I dessa fall är givetvis även den nedre spegeln försedd med hål.
Lite mer om Mirage finns i Wikipedia-artikelnParabolic_reflectorApplications . Här är historien bakom Mirage (från www.grand-illusions.com):
Tack Mette och Sven från Astronomi för värdefull input om spegelsystem!
Efter lite problem att identifiera spegelsystemet (tack Carina och Thomas!) har jag slutligen hittat tillräckligt bra dokumentation för att kunna beskriva hur det fungerar. Spegelsystemet heter heter 'Mirage® 3D Hologram Maker' eller 'Mirascope'. De flesta sajter man hittar med en Google-sökning är bara försäljning av Miragen och ingen förklaring. Länk 1 var emellertid bättre med en ganska detaljerad beskrivning. Där fanns även en YouTube-video som visar hur det ser ut (klicka på högerpilen för att starta):
Här är en demo för en skolklass som en del av en optiklektion. Videon visar bland annat hur man kan belysa den reella bilden med en ficklampa:
Lite mer sökande gav länk 2, som verkligen beskriver hur det fungerar. Bilderna nedan kommer från denna sida.
För det första så är det inte ett riktigt hologram - det ser bara ut som ett hologram. Ett hologram bygger på interferens med (normalt) en laserstråle. Denna konstruktion innehåller bara två paraboliska konkava speglar vända mot varandra.
Låt oss börja med att diskutera reella och virtuella bilder. Om man riktar ett vanligt teleskop med en positiv lins mot ett föremål (figur a nedan) och tittar på fokalplanet från sidan så ser man ingenting eftersom synfältet i kikaren är mycket begränsat. Den reella bilden i fokalplanet kan endast betraktas från en riktning rakt motsatt riktningen mot objektivet. Detta är var okularet normalt finns.
En vanlig spegel (figur b) ger en bild belägen bakom spegeln dit inga ljusstrålar når. Detta kallas för en virtuell bild. Bilden ser ut att komma från bakom spegeln, men där finns (eftersom det inte finns några ljusstrålar där) inget som kan fångas upp på en skärm.
Figur c visar hur en parabolisk spegel fungerar. Ljus från fokalpunkten kommer att gå ut som ett parallellt knippe i optiska axelns (parabelns storaxel, spegelns symmetriaxel) riktning. Omvänt så kommer ljus som infaller parallellt med optiska axeln (från ett avlägset föremål) att samlas i fokalpunkten.
Figur d visar hur Mirage är konstruerad. Den nedre spegeln (A) har sitt fokus nära den övre spegelns (Bs) plan. Fokus för B ligger på samma sätt i As plan.
Man kan nu förstå strålgången i figur e. En stråle från t.ex. knorren kommer ju nästan från fokalpunken för spegel B, och kommer alltså att speglas så att den kommer parallellt med optiska axeln. Den kommer sedan att speglas av spegel A mot dess fokus. Ljusstrålar i olika riktningar kommer att bygga upp en fullständig reell bild av föremålet nära fA. Det ser alltså ut som om grisen är i punkten fA och inte i punkten fB. Enda skillnaden är att den avbildade grisen är roterad 180 grader i horisontalplanet.
Observera att föremålet i fB är skymt av spegeln B eftersom man tittar från sidan. Uppifrån ser man ingen bild, men man ser föremålet.
Varför ser man bilden från sidan i Mirage men inte i fallet med den positiva linsen i figur a? I fallet Mirage är synfältet mycket stort, så bilden blir till en fullständig en 3d-kopia av objektet som kan betraktas från alla riktningar. För den positiva linsen är synfältet som sagt mycket begränsat, så det finns inga ljusstrålar som går ut åt sidorna.
Hur var det med belysningen av bilden i den andra videon? Även en reell bild på den lilla grisen är, som man märker om man petar på den, immateriell. Hur kan den då reflektera ljus från ficklampan? Det kan den naturligtvis inte, utan det är så att ljuset från lampan går samma men omvända vägen som ljuset från föremålet. Det är alltså föremålet som belyses, men via två reflektioner i först den nedre och sedan den övre spegeln.
Mirage-principen är inte bara en kul grej, utan konstruktionen används som aberationskorrigerare i teleskop och kallas då av uppenbar anledning 'clam-shell corrector'. I dessa fall är givetvis även den nedre spegeln försedd med hål.
Lite mer om Mirage finns i Wikipedia-artikeln
Mirage was originally discovered over 30 years ago, when a member of staff at the University of California at Santa Barbara was cleaning around a stack of searchlight reflectors (which are parabolic reflectors of course!) when he noticed that he was trying to clean off some 'dust' that turned out not to actually be there! He showed this to one of the physics professors, and the two of them started making a commercial product, based around the phenomenon that they had accidentally discovered.
Tack Mette och Sven från Astronomi för värdefull input om spegelsystem!
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.
Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar

