Vill du ha ett snabbt svar - sök i databasen
600 frågor / svar hittades
Hej! En elev kom och ställde följande fråga till mig: Johan, väger en diskett mer, lika mycket eller mindre när man har skrivit på den jämfört med när den är tom? Vad jag tror måste energin öka på disketten i och med att man ordnar magnetfältet på disketten. Frågan är då om detta har med vikten att göra?
/Johan R, Bergaskolan, Malmö 1999-01-26
Din förmodan är alldeles riktig. En magnetiserad diskett har högre energi än en omagnetiserad, och all energi väger ju enligt E = mc2. Den oskrivna disketten är ju inte omagnetiserad, den är ju formaterad. Formateringen innebär antagligen maximal magnetisering, så när man skriver på disketten minskar man magnetiseringen och därmed också massan. Masskillnaden är förstås så liten, att ingen våg i världen kan mäta den.
/KS 1999-03-30
Hej ! Mina elever undrar varför gaserna i luften inte skiktar sig efter molekylvikten. Hälsning Mohammed
/Mohammed E, Ärvingeskolan, Kista 1999-01-28
Den nedre delen (upp till ungefär 12 km)av jordens atmosfär kallas troposfären. Ordet kommer av det grekiska tropein, som betyder vända. Genom vertikala rörelser sker här en effektiv omrörning, så eventuell tendens till skiktning elimineras effektivt. Ovanför, i stratosfären, finns faktiskt en viss tendens till skiktning, så att de lättare molekylerna når högre upp. Det beror huvudsakligen på att de, vid en given temperatur, har högre hastighet än de tyngre.
/KS 1999-03-30
1) I den högre fysiken (alltså den man läser efter gymnasiet) så har jag hört talas om att man ofta pratar om vektorer. Vektorer i matematiska sammanhang vet jag vad det är. Men i fysiken, kan t.ex. fart tydligen beskrivas som en vektor. Varför det? Fart är ju bara vilken hastighet man har alltså 100 km/h t.ex.
2) Vidare, och detta talar man nog redan om i gymnasiet, så talar man ofta om normalvektorn. Om man t.ex. har ett föremål på ett bord, så finns det en vektor som vill dra ner föremålet, gravitationen alltså, men sen finns det också tydligen en vektor som pekar uppåt. Det har jag svårt att förstå. Vad är det för kraft som pekar uppåt? Gravitationen känner jag ju av men någon kraft som pekar uppåt känner jag inte av. Vidare, kan man översätta normalkraft (och andra krafter kanske) till de fyra grundkrafterna i naturen?
3) Derivering. Varför handlar fart, acceleration, m.m. om derivering? Jag har aldrig riktigt förstått det, och skulle vilja få ett bra svar på det. Vidare om man vet accelarationen så kan man tydligen integrera och då få farten. Hur då? Integrering ger ju en area under en kurva, väl?
/Mårten B, LTH, Lund 1999-01-31
1) Vanligt är att man använder hastighet för vektorn, medan fart är vektorns absolutbelopp.
2) Eftersom föremålet på bordet inte rör sig, måste det finnas en kraft som precis motverkar tyngdkraften.
3) Hastigheten är tidsderivatan av läget. Accelerationen är tidsderivatan av hastigheten (alltså hastighetsändringen). I en raket sitter en accelerometer. Det är ett instrument som mäter accelerationen i x, y och z. En dator gör kontinuerligt integration med avseende på tiden. Det ger hastigheten. Samtidigt integreras hastigheten med avseende på tiden. Det ger läget. Det är faktiskt så det går till i praktiken. Integralkalkyl handlar inte bara om ytor.
/KS 1999-02-05
Hej! Jag har lite funderingar kring ett fenomen. Om man har en tio meter lång stav i rymden och vrider den runt ena änden som en klockvisare så kommer man ju accelererar upp den i en viss hastighet och denna kommer ju vara större ju längre ut man kommer. Om man sen förlänger denna mer och mer så borde den yttersta hastigheten öka och till slut vara väldigt nära ljushastigeten relativt till utgångspunkten. Stämmer detta?
/Robin S, S:T Jacobi Gymnasium, Stockholm 1999-02-02
Jo, i princip kan man komma nära ljushastigheten, men aldrig över. Man brukar säga, att relativitetsteorin inte tillåter stela kroppar.
/KS 1999-02-02
Vad är det som gör att vissa cyklar "vill välta" när man släpper styret medans vissa kan man cykla utan problem.
/Olof S, Teknikum, Växjö 1999-02-04
Styrstången på en cykel lutar. Dra en linje längs styrstången, och lägg märke till var den når marken. Är det framför det område där hjulet berör marken? I så fall blir styrningen stabil när man släpper styret. Är det på eller bakom det området, blir styrningen instabil. Man kan inte släppa styret.
Graden av stabilitet beror på avståndet mellan de två punkterna. Böjen på framgaffeln minskar det avståndet, och minskar därmed stabiliteten. Utan böjen hade cykeln varit ganska tungstyrd.
/KS 1999-02-05
Vad innebär Newtons andra lag
/Rosaline B, Hvitfeldtska, GBG 1999-02-05
Kraften är lika med accelerationen gånger massan ( F = a m). Accelerationen = hastighetsändringen per tidsenhet (tidsderivatan av hastigheten).
/KS 1999-02-05
Hej och tack för svaren på mina frågor. Fast det var inte riktigt de svaren som mina frågor rörde. De svar jag fick har jag redan sett i läroböcker. Det jag menade var följande, lite förtydligat: 1.) Jag förstår att man som ni säger d e f i n i e r a r hastighet som en vektor. Men jag skulle vilja ha en pedagogisk förklaring på VARFÖR hastighet (som är t.ex. 100 km/h) kan vara en vektor (som är en riktad sträcka). En riktad sträcka har ju storheten längd, och hastighet storheten längd/tid. Hur går det ihop? Jag känner mig lite förvillad där. Alltså: varför beskrivs hastighet som en vektor? 2.a) Jag förstår inte hur det kan finnas en kraft som motverkar gravitationen på det viset. Det behöver väl inte finnas en kraft, det räcker väl med att bordet är ivägen, eller? Jag kan ju t.ex. inte känna av den kraften som ni talar om, på samma sätt som jag kan känna av gravitationen, det går ju t.ex. inte att förnimma en kraft som drar saker uppåt (det har iallafall aldrig jag känt av). b) Jo, jag undrade också där om detta på något sätt har någon anknytning till de fyra naturkrafterna i naturen (starka och svaga kärnkraften osv). För brukar man inte tala om att man vill förklara allt i naturen med hjälp av dessa? 3.) Det har jag som sagt redan läst i en lärobok. Min fråga är VARFÖR hastigheten är tidsderivatan av läget, och tvärtom när man integrerar. Jag skulle vilja ha någon pedagogisk konkret motivering till detta. När man definierade hastighet en gång i tiden måste man väl ha vetat vad man gjorde. T.ex. hur kan derivatan av läget ge hastigheten, det lilla jag kan om derivata är bara att derivatan är riktningskoefficienten. Hur blir det hastighet? Med vänligt hopp om ett bra svar... Hälsningar Mårten!
/Mårten B, MIC, UPPSALA 1999-02-05
1.) En vektor är inte en riktad sträcka. Det är när vi illustrerar den som vi ritar en riktad sträcka. Det är kanske lättare att förstå, om man betraktar ett vektorfält, till exempel det jordmagnetiska fältet. I varje punkt i närheten av jorden, har detta fält en viss riktning och en viss styrka. Det är precis vad som behövs för att bilda en vektor (som kan variera med tiden). Den vektorn är inte en sträcka, den mäter vi i tesla (T).
2.a) Newtons andra rörelselag säger att kraften är lika med accelerationen gånger massan ( F = a m ). Föremålet på bordet ligger stilla. Alltså är både hastighet och acceleration lika med noll. Då måste kraften vara noll. Då måste det finnas en kraft, som precis motverkar tyngdkraften. Den kan bara komma från bordet. Känner du inte av stolen du sitter på?
b) Detta är ren klassisk mekanik, och vi behöver inte blanda in de fenomen du nämner.
3.) Inom fysiken definierar vi hastigheten som tidsderivatan av läget. Och definitioner behöver man inte förklara. Men naturligtvis har det en praktisk bakgrund. Vi vill undersöka hur långt vi kommer om vi går i en timmes tid. Svaret blir kanske 6 km. Vi säger då att gånghastigheten i medeltal var 6 km/tim (om vi gick rakt). När vi dividerar sträckan med tiden, gör vi faktiskt en skattning av tidsderivatan av läget.
/KS 1999-02-05
Hur fort ska man köra mot ett trafikljus som visar rött så att det ser ut att visa grönt ?
/Lars B, Pauli, Malmö 1999-02-08
Man kan härleda följande formel:
v/c = (1 - (L1/L2)2) / (1 + (L1/L2)2)
v = hastigheten
c = ljushastigheten
L1 = våglängden för grönt ljus
L2 = våglängden för rött ljus
Ta reda på våglängderna och räkna själv. Får du nånting i stil med 40000 till 60000 km/s, har du nog räknat rätt. Men kör du så fort tar dom säkert körkortet.
Hur hög blir hastigheten i km/tim?
/KS 1999-02-08
Hej. Det finns ju flera supersträngteorier och M-teori,
så jag undrar vart man kan läsa om det mer för att lära sig tillräckligt för att förstå skilnaden mellan dem. Vet ni något ställe på Internet och någon bok/tidskrift som behandlar ämnet tillräckligt utförligt? I vilken mån är M-teorin oformulerad?
Vad är c (ljushastigheten) i för enhet? Jag utgick från formeln E=mcc, och där var E angiven i J och m i Kg. Då var alltså
cc angiven i J/Kg, men vad är roten ur (J/Kg)? Givetvis kan de ju vara så att c är enheten, men jag har inte grepp om vad c betyder.
Ps. Vart tog svaren på mina tidigare ställda frågor vägen?
/Hananja R, Bergska, Finspång 1999-02-08
I svaret till frågan nedan hittar du en bra hemsida om strängar.
J/kg är faktiskt detsamma som (m/s)2. Utnyttja J = Nm och N = kgm/s2.
Vi kan tyvärr inte svara på alla frågor. I synnerhet frågor med många
delfrågor i vitt skilda ämnen passar illa i vår databas.
/KS 1999-02-08
Jo, jag ska hålla ett litet föredrag om RELATIVITETSTEORIN. Ett ämne som kanske inte är det lättaste. Jag har samlat lagom med teoretisk fakta, men skulle vilja ha ett experiment som grädde på toppen. Har ni förslag på hur man kan visa att tidsdilatationen verkligen fungerar?
/Markus A, Komvux, Sjöbo, Sjöbo 1999-02-08
Kanske inte ett experiment, men ett bra exempel.
Först ett par definitioner:
Kosmiska strålningen består huvudsakligen av atomkärnor med mycket höga energier (mest väte). När de kolliderar med luften på cirka 20 km höjd, uppstår en uppsjö av olika partiklar. De flesta är kortlivade och sönderfaller snabbt. En av sönderfallsprodukterna kallas myon, och på grund av sina egenskaper, är den mycket lite benägen att kollidera med kärnorna i luften. Den försvinner för det mesta genom att den sönderfaller. Hur långt går den?
Myonens medellivslängd är 2.210-6 s. Antag att den går nära ljushastigheten (300000 km/s). Då får vi en sträcka på
300000 2.210-6 = 0.6 km = 660 m.
Ändå är det så, att de flesta partiklar vi kan registrera här nere är myoner. Genom en människa far det typiskt 30 - 40 högenergetiska myoner varje sekund. De överlever hit ner på grund av tidsdilatationen. De har så hög hastighet att tiden går mycket långsammare för dem, se översta formeln i bilden nedan. En myon med en Lorentz-faktor på 1000 kan i princip gå 660 km. Sådana myoner är inte alls ovanliga. För den myonen går tiden 1000 gånger långsammare (från oss sett).
Jaha, OK men sett från myonen då? Där går ju tiden med "normal" hastighet och myonen kan väl inte hinna ner till markytan innan den sönderfaller? Jo, det gör den därför att längdkontraktionen, se nedersta formeln nedan, gör att den sträcka myonen måste tillryggalägga är mycket kortare (sett ur myonens perspektiv).
Det är klart att resultatet att myonen hinner ner till marken innan den sönderfaller måste vara samma oberoende av om vi betraktar myonen från marken eller om vi följer med den ner genom luften.
Se vidare
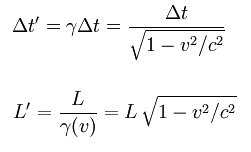
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.
Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar

