Vill du ha ett snabbt svar - sök i databasen:
Låda dras uppför lutande plan
Gymnasium: Kraft-Rörelse - friktion, lutande plan [20415]
Fråga:
Om man drar en låda med konstant hastighet uppför ett lutande plan och ska undersöka verkningsgraden för olika vinklar. Arbetet ses som den tillförda energin och lägesenergin ses som den nyttiga energin.
Våra resultat visar att större vinklar ger större verkningsgrad. Är detta sant? Varför/varför inte?
/Denizé Z, TBS, Örebro 2016-11-22
Om man drar en låda med konstant hastighet uppför ett lutande plan och ska undersöka verkningsgraden för olika vinklar. Arbetet ses som den tillförda energin och lägesenergin ses som den nyttiga energin.
Våra resultat visar att större vinklar ger större verkningsgrad. Är detta sant? Varför/varför inte?
/Denizé Z, TBS, Örebro 2016-11-22
Svar:
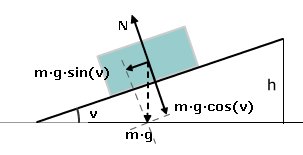
För att dra lådan uppför planet krävs en kraft som är lika med summan av friktionskraften µ·N=µ·m·g·cos(v) och tyngdkraftens komposant m·g·sin(v), alltså dragkraften, se länk 1 och nedanstående figur från länk 1:
F = µ·m·g·cos(v) + m·g·sin(v)
Potentiell energi på höjden h: mgh
Arbete: (µ·m·g·cos(v) + m·g·sin(v))·h/sin(v)
Verkningsgrad = e = Potentiell energi/Arbete
e = sin(v)/((µ·cos(v) + sin(v)) = 1/(µ·cot(v) + 1)
Låt oss se om detta är rimligt. Utan friktion (µ=0) ger e=1 som sig bör.
Om vinkeln v=0o blir e=0. Om v=90o blir e=1. Dessa extremfall motsvarar mycket friktion (lång sträcka, hög normalkraft) och ingen friktion (lådan dras vertikalt utan att röra planet).
Om v=45o och µ=0.2 blir e=1/(0.2+1)=0.83.
Som du ser är det korrekt att stor vinkel ger högre verkningsgrad.
För att dra lådan uppför planet krävs en kraft som är lika med summan av friktionskraften µ·N=µ·m·g·cos(v) och tyngdkraftens komposant m·g·sin(v), alltså dragkraften, se länk 1 och nedanstående figur från länk 1:
F = µ·m·g·cos(v) + m·g·sin(v)
Potentiell energi på höjden h: mgh
Arbete: (µ·m·g·cos(v) + m·g·sin(v))·h/sin(v)
Verkningsgrad = e = Potentiell energi/Arbete
e = sin(v)/((µ·cos(v) + sin(v)) = 1/(µ·cot(v) + 1)
Låt oss se om detta är rimligt. Utan friktion (µ=0) ger e=1 som sig bör.
Om vinkeln v=0o blir e=0. Om v=90o blir e=1. Dessa extremfall motsvarar mycket friktion (lång sträcka, hög normalkraft) och ingen friktion (lådan dras vertikalt utan att röra planet).
Om v=45o och µ=0.2 blir e=1/(0.2+1)=0.83.
Som du ser är det korrekt att stor vinkel ger högre verkningsgrad.
** Frågelådan är stängd för nya frågor tills vidare **
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.

Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.

Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar
