Svar:
Dennis! Egentligen svarar vi inte på räkneproblem, men detta var faktiskt riktigt kul, så vi gör ett undantag. Problemet innehåller dels uppdelning av en kraft i komposanter och dels tillämpning av energins bevarande.

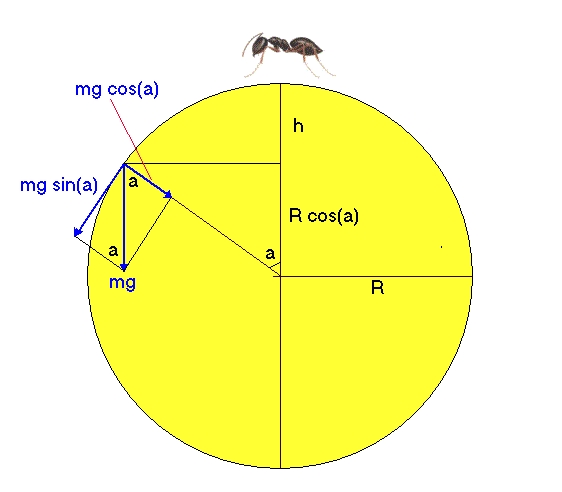
Vi delar upp gravitationskraften mg i en tangentiell komposant, mg sin(a), och en radiell, mg cos(a), se nedanstående bild. Det är alltså den växande tangentiella komposanten som accelererar myran, och den radiella som håller myran kvar på klotet. Så länge myran har kontakt med klotet rör den sig i en cirkelbana med radien R. Efter ett tag kommer den radiella komposanden ha minskat och myrans hastighet v ökat så att myran förlorar kontakten med klotet. För denna punkt gäller

mv²/R = mg cos(a)

dvs

v² = Rg cos(a) (1)

För att beräkna v använder vi förutsättningen att vi inte har någon friktion. Vi kan då använda energiprincipen: den potentiella energin i startpunkten är lika med rörelseenergin i punkten där kontakten med klotet förloras:

mgh = mg(R - R cos(a)) = mv²/2

dvs

v² = 2g(R - R cos(a)) (2)

Om vi sätter in uttrycket för v² från (1) får vi

Rg cos(a) = 2g(R - R cos(a))

cos(a) = 2 - 2 cos(a)

cos(a) = 2/3

vilket är svaret du gav. Vinkeln a är alltså c:a 48 grader.

/fa

/Peter E 2012-12-19