Svar:
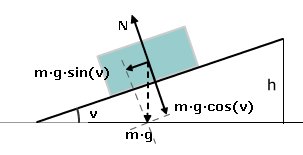
För att dra lådan uppför planet krävs en kraft som är lika med summan av friktionskraften µ·N=µ·m·g·cos(v) och tyngdkraftens komposant m·g·sin(v), alltså dragkraften, se länk 1 och nedanstående figur från länk 1:

F = µ·m·g·cos(v) + m·g·sin(v)

Potentiell energi på höjden h: mgh

Arbete: (µ·m·g·cos(v) + m·g·sin(v))·h/sin(v)

Verkningsgrad = e = Potentiell energi/Arbete

e = sin(v)/((µ·cos(v) + sin(v)) = 1/(µ·cot(v) + 1)

Låt oss se om detta är rimligt. Utan friktion (µ=0) ger e=1 som sig bör.

Om vinkeln v=0^o blir e=0. Om v=90^o blir e=1. Dessa extremfall motsvarar mycket friktion (lång sträcka, hög normalkraft) och ingen friktion (lådan dras vertikalt utan att röra planet).

Om v=45^o och µ=0.2 blir e=1/(0.2+1)=0.83.

Som du ser är det korrekt att stor vinkel ger högre verkningsgrad.

/Peter E 2016-11-22

Svar:
Massa och vikt definieras i fråga [16048]. Din massa är alltså konstant, men din vikt (egentligen tyngd) kan variera. Tyngd är påverkan av tyngdkraften, så den påverkas inte av lufttrycket.

På grund av atmosfären tillkommer emellertid en lyftkraft enligt Arkimedes princip, se fråga [13509].

Mount Everest har höjden 8848 m. I länk 1 finns en kalkylator som bland annat beräknar atmosfärens densitet på olika höjd:

0 m - 1.225 kg/m³

8848 m - 0.478 kg/m³

Säg att du väger 60 kg. Eftersom densiteten hos en människa är nära 1000 kg/m³ är volymen 0.06 m³. Ändringen i lyftkraften blir

(1.225-0.478)0.06 kg = 0.0448 kg = 45 g

Du blir alltså 45 gram "tyngre" på Mount Everest.

Det finns ett par effekter till som påverkar nettoresultatet, (ökat avstånd till masscentrum och jordens rotation) men dessa är små jämfört med lyftkraften orsakad av atmosfären.
/Peter E 2016-12-07

Svar:
För det första är det inte helt lätt att utföra tricket. Det kräver en hel del övning eftersom flaskan måste landa med botten nedåt. I videon nedan finns några lyckade försök - en del så lyckade att man undrar om de inte är fejkade :-).



I länk 1 finns en avancerad förklaring, men jag tror man krånglat till problemet onödigt mycket. Man förklarar inte heller varför flaskan inte studsar som den gör när man släpper den rakt ner.

Jag har gjort lite egna experiment med en 1.5 liters ICA apelsinsaftflaska till en tredjedel fylld med vatten.

Det är helt korrekt att flaskan välter nästan varje gång om man bara släpper den med botten nedåt, trots att tyngdpunkten är ganska låg. Detta beror säkert på att kontakten med underlaget får flaskan och vattnet att samtidigt studsa uppåt - vattnet befinner sig ju hela tiden längst ner i flaskan. En liten avvikelse från vertikalen ger en rotation som får flaskan att välta.

När man i stället kastar flaskan så att den snurrar exakt ett varv innan den landar har en del av vattnet flyttats högre upp i flaskan. Denna landar och försöker studsa uppåt. Innan den hinner någon vart kommer vattnet att kollidera med botten på flaskan, och flaskan trycks tillbaka till underlaget och ställer sig stadigt.
/Peter E 2016-12-07

Svar:
Jodå, det finns massor av information om suprafluiditet på webben, men för Wikipedia får du (som ofta) gå till den engelska artikeln Superfluidity.

Suprafluiditet kallas det fenomen som gör att vissa ämnen vid låga temperaturer har en fluid fas som flödar utan viskositet, så kallade "suprafluider". Ett exempel är helium-isotopen helium-4, en boson, som vid temperaturer under 2,186 kelvin (-270,964 °C) uppvisar sådana egenskaper. Suprafluiditet

Här är ett experiment med ⁴He:



Vid mycket låga temperaturer hamnar många av heliumatomerna i det lägsta kvantmekaniska tillståndet (grundtillståndet) Detta är möjligt eftersom ⁴He är en boson med heltaligt spinn, och den behöver därför inte lyda paulipricipen (se fråga [18298]). Energin hos atomerna i grundtillståndet är för låg för att spridning till ett högre tillstånd skall kunna ske. Spridning är alltså omöjlig och viskositeten blir noll.

Ännu märkligare än viskositeten noll är att supraflödande He kan ta sig över hinder, se nedanstående figur från Rollin_film. Detta kallas Onnes-effekten som uppstår genom att kapillärkrafter dominerar över tyngdkraften och viskositeten.

/Peter E 2016-12-14

Svar:
Lika säker som att Pythagoras sats (Pythagoras_sats) innehåller kvadrater! Man kan härleda längdkontraktionen från Lorentz-transformationen: länk 1, Length_contraction, Derivations_of_the_Lorentz_transformations.

Man kan göra en enkel geometriskt härledning av tidsdilationen, se nedanstående figur. Enda antagandet är att ljushastigheten c är konstant oberoende av koordinatsystemets rörelse.

Vi undersöker först hur en klocka bestående av en ljusstråle som går uppåt och reflekteras av en spegel. I övre delen av figuren visas hur klockan uppför sig när den inte rör sig. I nedre delen rör sig klockan med hastigheten v. För att ljusstrålen skall komma tillbaka till samma punkt måste den färdas lite längre sträcka. Om vi tillämpar Pythagoras sats på den rätvinkliga triangeln får vi

D² = L² + (v Dt'/2)²

(c Dt')² =
(c Dt)² +
(v Dt')²

Dt' sqrt(1-v²/c²) = Dt

Dt' = Dt g

där

g = 1/sqrt(1-v²/c²)

I Length_contractionTime_dilation visas att längdkontraktionen av en linjal med längden L₀ gör att linjalen tycks ha längden

L' = L₀ / g

där L' är mindre än L₀.

Se även fråga [20002] och [2697].

/Peter E 2017-01-05

Svar:
Emma och Melker!
Fysiken bakom golf är mycket komplicerad, men man kan förstå en hel del genom att förenkla problemen. Teorin innehåller ofta fria parametrar som anpassas till mätdata.

I boken The Physics of Golf av Theodore P Jorgensen görs en ganska omfattande analys, men det är inte helt lätt att förstå detaljerna.

Låt oss titta på ert problem som är det enklaste: en central stöt mellan ett klubbhuvud med massan M och en boll med massan m.
Klubbhuvudet har 0 graders loft, så vi har inget spinn. Precis före stöten är klubbhuvudets hastighet V. Efter stöten är klubbhuvudets hastighet u och bollens hastighet är v. Vi antar att stöten är elastisk så att vi inte har några förluster som t.ex. inre friktion pga bollens eller klubbhuvudets deformering. Vid stöten måste vi bevara rörelsemängd och kinetisk energi:

MV = Mu + mv (1)

MV²/2 = Mu²/2 + mv²/2 (2)

Om vi eliminerar u (klubbhuvudets hastighet efter stöten) i (2) med hjälp av (1) får vi för bollens utgånghastighet

v = 2MV/(m+M) = 2V/(m/M + 1) (3)

(I länk 1 finns mer detaljer av härledningen med andra beteckningar.)

Mycket av vad som följer är från kapitel 9 i The Physics of Golf (se ovan).

Om m är mycket mindre än M får vi att v=2V. Detta är alltså den teoretiskt högsta möjliga hastigheten för bollen. Om m=M får vi att v=V (klubbhuvudet är i vila efter stöten). Bollens utgångshastighet är alltså proportionell mot klubbhuvudets hastighet: v = kV. Konstanten k beror av deformationsförluster (se studskoefficient i fråga [20384]) och klubbans loft.

Typiska värden för k är 1.46, 1.30 och 1.12 för driver, järnfemma och järnnia, respektive. Klubbhastigheten för en bra spelare är ungefär 45 m/s vilket ger en bollhastighet med driver av 1.4645=66 m/s. Detta ger en slaglängd på c:a 225 m.

Med ett flexibelt skaft kan man som en hygglig approximation anta att klubbhuvudet vid bollträffen uppför sig som en fri kropp.

Ju större loft en klubba har desto mer spinn får bollen efter träffen. Spinnet ger genom dimplarna och Magnus-effekten en lyftkraft och turbulens som minskar luftmotståndet (se fråga [14113]). Detta gör att bollen flyger längre.

Spinnet kostar emellertid genom att k blir mindre (se ovan). Detta reflekterar faktumet att en del av den överförda energin går till bollens rotationsenergi.

Parentes: Uttrycket v=2V för ett tungt klubbhuvud kan vi få med ett enklare resonemang. Vid en fullständigt elastisk kollision mellan två objekt bevaras den relativa hastigheten. I ovanstående exempel är relativa hastigheten V (klubbhuvudets hastighet). Efter stöten fortsätter klubbhuvudet med hastigheten V och bollen har hastigheten V i förhållande till klubbhuvudet. Bollens hastighet i förhållande till marken är då v=V+V=2V.

Här är fler frågor som behandlar golf: golfboll. Se även länk 2.
/Peter E 2017-01-09

Svar:
Om satelliten rör sig i en cirkelbana runt planeten utförs inget arbete eftersom rörelsen är i tangentens riktning och kraften är riktad in mot cirkelns centrum. Dessa riktningar är vinkelräta mot varandra, vilket betyder att ingen del av kraften är i rörelseriktningen. Arbete är ju kraftväg i rörelserikningen, se fråga [13327].

För en elliptisk bana finns det (utom i närmsta och mest avlägsna punkten) en komponent av gravitationskraften i rörelseriktningen. Då är det den totala energin E = U + K, där U är potentiella energin och K den kinetiska energin, som bevaras. Vi får alltså ett utbyte mellan U och K så att E är konstant.

Sedan är det en annan sak att det kostar mycket arbete (raketkraft) att placera en satellit i en bana.

Se gravity assist för beskrivning av en teknik där man kan "stjäla" rörelseenergi från en planet till en rymdsond som rör sig i en hyperbelbana.
/Peter E 2017-02-15

Svar:
Förvånansvärt liten skillnad vad gäller framdrivning. Man använder fortfarande ett fast eller flytande bränsle som brinner vid hög temperatur. Restprodukterna far ut med stor hastighet och får raketen att accelerera. Sluthastigheten bestäms av raketekvationen, se fråga [1827]. Styrsystem och övrig instrumentering har emellertid utvecklats mycket.

Det finns ett par nya idéer som dock inte kommit särskilt långt: jondrift (se fråga [14044]) och rymdsegel (se fråga [17100]).

Se vidare Raket och Rocket.

/Peter E 2017-03-02

Svar:
Hej Anton! Eftersom du refererar till hastigheter nära ljushastigheten så duger inte de uttryck du använder. Du måste använda uttryck enligt den speciella relativitetsteorin. Detta diskuteras i Schwarzschild_radiusRelativistic_circular_orbits_and_the_photon_sphere.

Från Keplers lag (fråga [12644]) får man för en cirkulär bana, som du mycket riktigt säger,

r = GM/v²

Detta gäller emellertid bara för icke-relativistiska värden på v. Det relativistiska uttrycket ger

(v/c)² (r/r_S - 1) = 1/2

För v = c blir detta

r = 3r_S/2

där

r_S = 2GM/c² (se fråga [18930])

Detta betyder att banan i själva verket ligger utanför Schwarzschildradien r_S. Denna bana kallas foton-sfären eftersom fotoner med hastigheten c kan röra sig i en stabil cirkelbana.

Se även länk 1 (figuren nedan) och Photon_sphere.

/Peter E 2017-05-22

Svar:
Elina! Man kan resonera på olika sätt.

Man kan se svängningen hos strängen som en harmonisk svängning, se fråga [18042]. Spänningen i strängen motsvarar konstanten k i Hookes lag. Då k motsvarar spänningen kommer högre spänning ge en högre ton (kortare svängningstid). Om strängen är tjockare har den högre massa (m i formeln), vilket ger mer motstånd för svängningen, större T och därmed lägre ton.

Längden på strängen är också av betydelse eftersom strängarna är fixa i båda ändarna. Svängningen måste alltså har en nod (strängen rör sig inte) i båda ändar. Den lägsta möjliga tonen motsvarar då 1/2 våglängd - grundtonen. Av övriga toner försvinner alla utom några s.k. övertoner som har en våglängd på 1/2, 1/3,... gånger grundtonen. Dessa övertoner har alltså kortare våglängd och därmed högre frekvens.

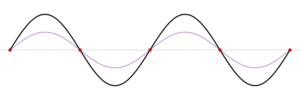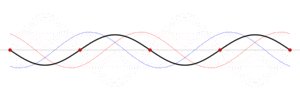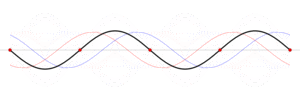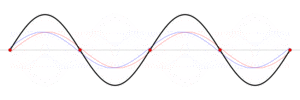
Grundtonen och övertoner är stående vågor som kan ses som två vågor som rör sig åt olika håll, se bilden nedan och Stående_våg. Grund- och övertonerna bestäms då av vågornas hastighet och strängens längd. Längre sträng betyder att det tar längre tid för de rörliga vågorna att gå längs strängen. Längre tid betyder lägre frekvens och alltså en lägre ton.

Se även String_instrumentChanging_the_pitch_of_a_vibrating_string och Stränginstrument.

/Peter E 2018-01-22