Vill du ha ett snabbt svar - sök i databasen
600 frågor / svar hittades
Varför pekar nosen på en bil som accelererar något uppåt?
Fråga:
Framdelen på en bil som accelerera snabbt pekar något uppåt, medan den i stället lutar neråt när bilen bromsar hastigt. Varför?
/Kadir S, SU, Stockholm 2015-01-08
Framdelen på en bil som accelerera snabbt pekar något uppåt, medan den i stället lutar neråt när bilen bromsar hastigt. Varför?
/Kadir S, SU, Stockholm 2015-01-08
Svar:
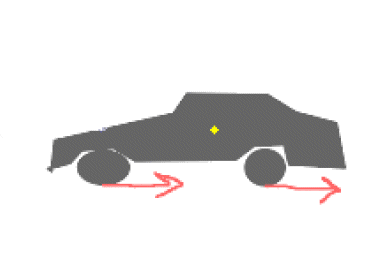
Därför att krafterna på hjulen har ett vridmoment med avseende på bilens masscentrum.
Låt oss först definiera vridmoment:
Begreppetvridmoment (Torque , vridmoment )
eller kraftmoment är en krafts förmåga att vrida en kropp kring en punkt. Vridmomentet t är proportionellt mot kraften F och mot momentarmen, det vill säga mot det vinkelräta avståndet r mellan kraftens verkningslinje och rotationscentrum. Vridmomentet med avseende på rotationscentrum är alltså:
t = Fr
SI-enheten för vridmoment är newtonmeter (Nm), se fråga [1157].
För en standardbil ligger masscentrum (gul prick i bilden nedan, se fråga [13477]), högre än hjulen. En accelererande eller bromsande kraft i hjulen kommer därför att skapa ett vridmoment som ger en rotation hos bilen. En bromsande kraft vill då rotera bilen moturs (nosen dippar) och en accelererande kraft vill rotera bilen medurs (nosen lyfts).
Därför att krafterna på hjulen har ett vridmoment med avseende på bilens masscentrum.
Låt oss först definiera vridmoment:
Begreppet
eller kraftmoment är en krafts förmåga att vrida en kropp kring en punkt. Vridmomentet t är proportionellt mot kraften F och mot momentarmen, det vill säga mot det vinkelräta avståndet r mellan kraftens verkningslinje och rotationscentrum. Vridmomentet med avseende på rotationscentrum är alltså:
t = Fr
SI-enheten för vridmoment är newtonmeter (Nm), se fråga [1157].
För en standardbil ligger masscentrum (gul prick i bilden nedan, se fråga [13477]), högre än hjulen. En accelererande eller bromsande kraft i hjulen kommer därför att skapa ett vridmoment som ger en rotation hos bilen. En bromsande kraft vill då rotera bilen moturs (nosen dippar) och en accelererande kraft vill rotera bilen medurs (nosen lyfts).
Gastryck i ballonger
Fråga:
Hej, jag har alltid förstått det som att det är ett övertryck i en ballong som blåses upp, annars skulle ju inte ballongen flyga iväg när man släpper den?
I en av de läroböcker (Impuls Fysik 1) som jag har finns det dock ett exempel (s.197) där man ska räkna ut den nya volymen på en heliumballong efter att den doppats i flytande kväve. I lösningen till problemet står det att "trycket i ballongen är lika stort som lufttrycket både före och efter nedkylningen, den är ju i tryckjämvikt med luften".
Jag blir inte klok på det här, det låter ju också rimligt att när man blåser upp en ballong så ökar trycket i ballongen för att antalet atomer i ballongen ökar. Därför expanderar balllongen till dess volymen är så stor att trycket inuti är lika stort som lufttrycket utanför, men det motsäger ju det jag inledningsvis sade.
Hur ska man tänka, vad är rätt? Är det materialet i ballongen som spelar roll här?
/Marilla A, Östra Gymnasiet, Trångsund 2015-01-30
Hej, jag har alltid förstått det som att det är ett övertryck i en ballong som blåses upp, annars skulle ju inte ballongen flyga iväg när man släpper den?
I en av de läroböcker (Impuls Fysik 1) som jag har finns det dock ett exempel (s.197) där man ska räkna ut den nya volymen på en heliumballong efter att den doppats i flytande kväve. I lösningen till problemet står det att "trycket i ballongen är lika stort som lufttrycket både före och efter nedkylningen, den är ju i tryckjämvikt med luften".
Jag blir inte klok på det här, det låter ju också rimligt att när man blåser upp en ballong så ökar trycket i ballongen för att antalet atomer i ballongen ökar. Därför expanderar balllongen till dess volymen är så stor att trycket inuti är lika stort som lufttrycket utanför, men det motsäger ju det jag inledningsvis sade.
Hur ska man tänka, vad är rätt? Är det materialet i ballongen som spelar roll här?
/Marilla A, Östra Gymnasiet, Trångsund 2015-01-30
Svar:
Problemet är att det finns två typer av ballonger. Ja, det är materialet som gör skillnaden.
Gummiballong som är elastisk och expanderar när man blåser upp den. För jämvikt måste denna ha högre gastryck än omgivningen för att kompensera för elasticiteten. Denna vill ju minska ballongens volym.
Plastballong som hela tiden har en fix volym. Denna ballong är inte elastisk, så trycket inne och utanför kan vara detsamma. Vid för lågt tryck i ballongen blir den skrynklig i stället för att dra ihop sig.
Se även fråga [554].
/Peter E 2015-01-30
Problemet är att det finns två typer av ballonger. Ja, det är materialet som gör skillnaden.
Gummiballong som är elastisk och expanderar när man blåser upp den. För jämvikt måste denna ha högre gastryck än omgivningen för att kompensera för elasticiteten. Denna vill ju minska ballongens volym.
Plastballong som hela tiden har en fix volym. Denna ballong är inte elastisk, så trycket inne och utanför kan vara detsamma. Vid för lågt tryck i ballongen blir den skrynklig i stället för att dra ihop sig.
Se även fråga [554].
/Peter E 2015-01-30
Varför är det svårare att balansera en kort pinne på fingret än en lång?
Fråga:
Hej!
jag har några frågor om balans. Varför är det svårare att balansera en kort pinne på fingret än en lång? Är förklaringen densamma som för varför det är lättare att balansera en pinne med en tyngd i toppen än en utan, alltså att tröghetsmomentet ökar? Eller har det även med själva längden på pinnen att göra?
Jag undrar även varför man balanserar lättare på en lina om man håller i en lång stång. Hur kan detta göra att man "sänker" sin tyngpunkt?
Hälsningar Anna
/Anna J, 2015-02-18
Hej!
jag har några frågor om balans. Varför är det svårare att balansera en kort pinne på fingret än en lång? Är förklaringen densamma som för varför det är lättare att balansera en pinne med en tyngd i toppen än en utan, alltså att tröghetsmomentet ökar? Eller har det även med själva längden på pinnen att göra?
Jag undrar även varför man balanserar lättare på en lina om man håller i en lång stång. Hur kan detta göra att man "sänker" sin tyngpunkt?
Hälsningar Anna
/Anna J, 2015-02-18
Svar:
Hej Anna! Det är lättare att balansera en lång pinne än en kort eftersom en lång pinne "faller" långsammare än en kort eftersom tröghetsmomentet är större för en lång pinne. Med en kort pinne hinner man helt enkelt inte med att reagera och att korrigera läget så att pinnen inte faller. Detta är analogt med det faktum att en lång pendel svänger långsammare än en kort, se fråga [14065].
Den effektiva längden på en pinne bestäms av tyngdpunktens (masscentrums) läge. En pinne med en tyngd i toppen har en större effektiv längd än en pinne utan tyngd vilket gör den lättare att balansera.
Här är en demonstration av effekten. Detaljerad förklaring finns i länk 1. Var försiktig om du vill utföra försöket så du inte förstör golvet (eller dina tår) om du misslyckas med balansakten!
Stången som en lindansare använder ger samma effekt som en längre pinne ovan: den ökar tröghetsmomentet för systemet och därmed tidskonstanten. Stången kan dessutom användas för att korrigera avvikelser hos masscentrum från lodlinjen genom linan, seTightrope_walkingBiomechanics .
/Peter E 2015-02-18
Hej Anna! Det är lättare att balansera en lång pinne än en kort eftersom en lång pinne "faller" långsammare än en kort eftersom tröghetsmomentet är större för en lång pinne. Med en kort pinne hinner man helt enkelt inte med att reagera och att korrigera läget så att pinnen inte faller. Detta är analogt med det faktum att en lång pendel svänger långsammare än en kort, se fråga [14065].
Den effektiva längden på en pinne bestäms av tyngdpunktens (masscentrums) läge. En pinne med en tyngd i toppen har en större effektiv längd än en pinne utan tyngd vilket gör den lättare att balansera.
Här är en demonstration av effekten. Detaljerad förklaring finns i länk 1. Var försiktig om du vill utföra försöket så du inte förstör golvet (eller dina tår) om du misslyckas med balansakten!
Stången som en lindansare använder ger samma effekt som en längre pinne ovan: den ökar tröghetsmomentet för systemet och därmed tidskonstanten. Stången kan dessutom användas för att korrigera avvikelser hos masscentrum från lodlinjen genom linan, se
/Peter E 2015-02-18
Varför försvinner såpbubblor om man tillsätter olja?
Fråga:
Hejsan! Vill veta varför alla såpbubblor i vasken försvinner när man häller på enstaka droppar olja i.
/Yasmin r, Malmö 2015-03-04
Hejsan! Vill veta varför alla såpbubblor i vasken försvinner när man häller på enstaka droppar olja i.
/Yasmin r, Malmö 2015-03-04
Svar:
Ensåpbubbla är ett tunt skikt av såpvatten som är fylld med luft. Hela objektet är sfäriskt. Såpbubblor används främst som leksak. Såpbubblor framställs genom att i vatten tillsätta diskmedel eller glycerol som sänker vattnets ytspänning så att ytskiktet blir mer elastiskt. Det möjliggör att man kan blåsa stora och förhållandevis hållbara bubblor via en ögla som doppas i vätskan. (Såpbubbla
)
För att förstå varför olja förstör såpbubblor måste vi förstå hur en såpbubbla är uppbyggd. Detta är utmärkt beskrivet i dokumentet under länk 1. Figuren och beskrivningen nedan kommer från detta dokument.
Såpmolekylerna kallas amfifiler. Det betyder att en del av molekylen gillar vatten (hydrofil) och att en annan del av molekylen avskyr vatten (hydrofob).
Molekylerna ser ut som små grodyngel med ett huvud som gillar vatten och en svans som hatar vatten. När sådana molekyler hamnar i vatten kommer så många som möjligt att leta sig till ytan så att "huvudet" kan vara i vattnet och "svansen" i luften., se figuren nedan. Väggen i bubblan består alltså av ett tunt lager vatten mellan lager av såpmolekyler med svansarna utåt.
Såpbubblor är emellertid ömtåliga och går lätt sönder på grund av yttre påverkan. Om en liten droppe av t.ex. olja fastnar på ytan störs den ordnade raden av amfifiler av attraktionen från oljedroppen, vattnet från det tunna skiktet läcker ut och bubblan går sönder.
Se även fråga [8628], [16513],Soap_bubble och länk 2.
En
)För att förstå varför olja förstör såpbubblor måste vi förstå hur en såpbubbla är uppbyggd. Detta är utmärkt beskrivet i dokumentet under länk 1. Figuren och beskrivningen nedan kommer från detta dokument.
Såpmolekylerna kallas amfifiler. Det betyder att en del av molekylen gillar vatten (hydrofil) och att en annan del av molekylen avskyr vatten (hydrofob).
Molekylerna ser ut som små grodyngel med ett huvud som gillar vatten och en svans som hatar vatten. När sådana molekyler hamnar i vatten kommer så många som möjligt att leta sig till ytan så att "huvudet" kan vara i vattnet och "svansen" i luften., se figuren nedan. Väggen i bubblan består alltså av ett tunt lager vatten mellan lager av såpmolekyler med svansarna utåt.
Såpbubblor är emellertid ömtåliga och går lätt sönder på grund av yttre påverkan. Om en liten droppe av t.ex. olja fastnar på ytan störs den ordnade raden av amfifiler av attraktionen från oljedroppen, vattnet från det tunna skiktet läcker ut och bubblan går sönder.
Se även fråga [8628], [16513],
Hur kan en Formel 1 bil dra fördel av luftmotståndet?
Fråga:
Hur kan en Formel 1 bil dra fördel av luftmotståndet?
/alexander , IES Lund, Lund 2015-11-29
Hur kan en Formel 1 bil dra fördel av luftmotståndet?
/alexander , IES Lund, Lund 2015-11-29
Svar:
Kul fråga Alexander! Ja, en F1-bil är helt beroende av luftmotståndet! Utan det hade bilen kört av i den första kurvan!
Det man först tänker på är att luftens rörelse i förhållande till bilen ger en bromsande kraft (engelska drag), vilket naturligtvis inte är positivt. Det finns emellertid gott om effekt i motorn för att motverka motståndet. Avgörande för snabbheten hos F1-bil är inte motorstyrkan utan väggreppet.
Karossen på bilen designas för att minimera "drag" (som uppkommer genom turbulens) och för att maximera nedåtkraften (engelska downforce). Nedåtkraften skapas av en konstruktion som liknar en flygplansvinge (se fråga [12891]) fast upp-och-ner.
Nedåtkraften adderas till tyngdkraften och utgör normalkraften. Friktionen, dvs väggreppet, är ju proportionellt mot normalkraften. Så större normalkraft ger bättre väggrepp vilket påverkar både acceleration, bromsförmåga och kurvtagning.
För att ytterligare öka "downforce" har F1-bilen vingar både fram och bak, se bilden nedan från Wikimedia. Man kan med en optimal kaross och vingar åstadkomma en "downforce" som överskrider tyngdkraften på bilen. Den skulle alltså teoretiskt kunna köras i taket!
De senaste åren har man infört en möjlighet att justera den bakre vingen under loppet. Detta kallas DRS (Drag Reduction System). När man vill köra om på en raksträcka kan man reducera "drag" och därmed få bättre acceleration. Man förlorar lite "downforce", så DRS deaktiveras automatiskt när man bromsar inför nästa kurva.
Se vidareFormula_One_carAerodynamics och Drag_reduction_system .
Kul fråga Alexander! Ja, en F1-bil är helt beroende av luftmotståndet! Utan det hade bilen kört av i den första kurvan!
Det man först tänker på är att luftens rörelse i förhållande till bilen ger en bromsande kraft (engelska drag), vilket naturligtvis inte är positivt. Det finns emellertid gott om effekt i motorn för att motverka motståndet. Avgörande för snabbheten hos F1-bil är inte motorstyrkan utan väggreppet.
Karossen på bilen designas för att minimera "drag" (som uppkommer genom turbulens) och för att maximera nedåtkraften (engelska downforce). Nedåtkraften skapas av en konstruktion som liknar en flygplansvinge (se fråga [12891]) fast upp-och-ner.
Nedåtkraften adderas till tyngdkraften och utgör normalkraften. Friktionen, dvs väggreppet, är ju proportionellt mot normalkraften. Så större normalkraft ger bättre väggrepp vilket påverkar både acceleration, bromsförmåga och kurvtagning.
För att ytterligare öka "downforce" har F1-bilen vingar både fram och bak, se bilden nedan från Wikimedia. Man kan med en optimal kaross och vingar åstadkomma en "downforce" som överskrider tyngdkraften på bilen. Den skulle alltså teoretiskt kunna köras i taket!
De senaste åren har man infört en möjlighet att justera den bakre vingen under loppet. Detta kallas DRS (Drag Reduction System). När man vill köra om på en raksträcka kan man reducera "drag" och därmed få bättre acceleration. Man förlorar lite "downforce", så DRS deaktiveras automatiskt när man bromsar inför nästa kurva.
Se vidare
Stora störtloppsåkare, igen
Fråga:
Fråga angående ”869”, där ni diskuterar massans betydelse för en störtloppsåkare.
I svaret påstås att en tyngre åkare får en högre hastighet med följande resonemang:
”Kraften som drar skidåkaren nedåt är ju proportionell mot massan, medan kraften som bromsar (luftmotståndet) är proportionell mot ytan. Vi får allstå en större kraft för den tyngre skidåkaren, medan luftmotståndet inte ökar lika mycket. Så om allt annat är lika så har en tyngre åkare en fördel.”
Jag förstår inte resonemanget kring hur en större kraft ger en större hastighet...
MITT RESONEMANG:
Hänvisningen är således till Newtons andra lag: F = ma.
Ett större föremål får ju en större kraft. Men: Detta är i mina ögon inte samma sak som att föremålet får en högre hastighet - det är ju en större massa som ska accelereras.
Galileis lag ger att två föremål som faller från samma höjd faller lika fort oberoende av vikt givet att fritt fall föreligger. Detta trots att det tyngre föremålet påverkas av en större kraft. I vardagen har vi inte fritt fall, utan ett motstånd. Men det blir inte med nödvändighet mindre om massan ökar.
På motsvarande sätt menar jag att skidåkaren kommer att omsätta lägesenergi i rörelseenergi: mgh = 0,5mv^2, dvs massan spelar ingen roll om luftmotståndet och friktionen från underlaget försummas (givet att åkaren inte ”stakar”).
Enligt det resonemanget att en tyngre åkare skulle vara snabbare, så måste det innebära att han får ett mindre motstånd. Jag har svårt att se hur luftmotståndet skulle minska med massan (vilket inte heller påstås). Återstår att den tyngre åkaren skulle ha mindre friktion, trots att friktionen är proportionell mot normalkraften (som beror av massan). Det skulle möjligen kunna vara sant om åkaren med sin större massa trycker ner snön och därmed påverkar friktionstalet till sin fördel (vilket är tveksamt i en välpreparerad backe).
Min förklaring till att en tyngre åkare skulle kunna ha en fördel är följande:
Utförsåkning är en krävande sport. Det är jobbigt att krypa ihop i störtloppsställning. Det krävs stora krafter för att kunna hålla emot i svängarna. Det gynnar en fysiskt vältränad person med stor muskelmassa. Att lägga på sig muskelmassa ger en större vikt. Kraftfullheten som åkare ger en större effekt än den uppbromsande friktionen från en ökad massa, varför en tyngre åkare borde ha fördel (förutsatt att massan sitter på rätt ställe).
/Philip L, 2015-12-08
Fråga angående ”869”, där ni diskuterar massans betydelse för en störtloppsåkare.
I svaret påstås att en tyngre åkare får en högre hastighet med följande resonemang:
”Kraften som drar skidåkaren nedåt är ju proportionell mot massan, medan kraften som bromsar (luftmotståndet) är proportionell mot ytan. Vi får allstå en större kraft för den tyngre skidåkaren, medan luftmotståndet inte ökar lika mycket. Så om allt annat är lika så har en tyngre åkare en fördel.”
Jag förstår inte resonemanget kring hur en större kraft ger en större hastighet...
MITT RESONEMANG:
Hänvisningen är således till Newtons andra lag: F = ma.
Ett större föremål får ju en större kraft. Men: Detta är i mina ögon inte samma sak som att föremålet får en högre hastighet - det är ju en större massa som ska accelereras.
Galileis lag ger att två föremål som faller från samma höjd faller lika fort oberoende av vikt givet att fritt fall föreligger. Detta trots att det tyngre föremålet påverkas av en större kraft. I vardagen har vi inte fritt fall, utan ett motstånd. Men det blir inte med nödvändighet mindre om massan ökar.
På motsvarande sätt menar jag att skidåkaren kommer att omsätta lägesenergi i rörelseenergi: mgh = 0,5mv^2, dvs massan spelar ingen roll om luftmotståndet och friktionen från underlaget försummas (givet att åkaren inte ”stakar”).
Enligt det resonemanget att en tyngre åkare skulle vara snabbare, så måste det innebära att han får ett mindre motstånd. Jag har svårt att se hur luftmotståndet skulle minska med massan (vilket inte heller påstås). Återstår att den tyngre åkaren skulle ha mindre friktion, trots att friktionen är proportionell mot normalkraften (som beror av massan). Det skulle möjligen kunna vara sant om åkaren med sin större massa trycker ner snön och därmed påverkar friktionstalet till sin fördel (vilket är tveksamt i en välpreparerad backe).
Min förklaring till att en tyngre åkare skulle kunna ha en fördel är följande:
Utförsåkning är en krävande sport. Det är jobbigt att krypa ihop i störtloppsställning. Det krävs stora krafter för att kunna hålla emot i svängarna. Det gynnar en fysiskt vältränad person med stor muskelmassa. Att lägga på sig muskelmassa ger en större vikt. Kraftfullheten som åkare ger en större effekt än den uppbromsande friktionen från en ökad massa, varför en tyngre åkare borde ha fördel (förutsatt att massan sitter på rätt ställe).
/Philip L, 2015-12-08
Svar:
Nej, resonemanget i fråga [869] är korrekt och, tycker jag, tydligt. Du antar att luftmotståndet kan försummas. Det är tvärtom så att luftmotståndet är den dominerande bromsande kraften vid hög hastighet (se länk 1, s 350). Du kan se det vid en störloppstävling. Om en åkare har dålig balans måste hon/han resa sig lite för att återfå balansen. Man ser tydligt på mellantiderna att den sämre aerodynamiken medför att farten minskar.
Det är klart att skidåkarens vikt bara är en parameter som bestämmer resultatet. God teknik och styrka att hålla emot g-krafter (se fråga [15970]) är självklart mycket viktiga -- Lindsey Vonn är relativt stor för en tjej (75 kg, 178 cm lång) men det är säkert den utmärkta tekniken som gör henne så överlägsen! Intressant är också att Anja Pärsson föredragit att vara lättare, med det var för att bli bättre i slalom, se länk 2.
Här är ett annorlunda resonemang som leder till samma slutsats:
Om vi antar att den dominerande bromsande kraften är luftmotståndet kan man härleda ett uttryck för sluthastigheten enligt nedanstående bild från fråga [15385].
Om vi stryker alla konstanter och låter ~ betyda proportionellt mot, så får vi sluthastigheten
Vt ~ sqrt(m/A) ~ sqrt(r3/r2) = sqrt(r)
I termer av massan m får vi eftersom m ~ r3:
Vt ~ sqrt(r) ~ (m1/3)1/2 = m1/6
Sluthastigheten ökar alltså som sjätte roten ur massan.
Se även fråga [18144].
Nej, resonemanget i fråga [869] är korrekt och, tycker jag, tydligt. Du antar att luftmotståndet kan försummas. Det är tvärtom så att luftmotståndet är den dominerande bromsande kraften vid hög hastighet (se länk 1, s 350). Du kan se det vid en störloppstävling. Om en åkare har dålig balans måste hon/han resa sig lite för att återfå balansen. Man ser tydligt på mellantiderna att den sämre aerodynamiken medför att farten minskar.
Det är klart att skidåkarens vikt bara är en parameter som bestämmer resultatet. God teknik och styrka att hålla emot g-krafter (se fråga [15970]) är självklart mycket viktiga -- Lindsey Vonn är relativt stor för en tjej (75 kg, 178 cm lång) men det är säkert den utmärkta tekniken som gör henne så överlägsen! Intressant är också att Anja Pärsson föredragit att vara lättare, med det var för att bli bättre i slalom, se länk 2.
Här är ett annorlunda resonemang som leder till samma slutsats:
Om vi antar att den dominerande bromsande kraften är luftmotståndet kan man härleda ett uttryck för sluthastigheten enligt nedanstående bild från fråga [15385].
Om vi stryker alla konstanter och låter ~ betyda proportionellt mot, så får vi sluthastigheten
Vt ~ sqrt(m/A) ~ sqrt(r3/r2) = sqrt(r)
I termer av massan m får vi eftersom m ~ r3:
Vt ~ sqrt(r) ~ (m1/3)1/2 = m1/6
Sluthastigheten ökar alltså som sjätte roten ur massan.
Se även fråga [18144].
Fritt fall med löst rep
Fråga:
Hej,
under våra fysikspecialiserings lektioner har vi diskuterat teorin bakom detta experiment, utan framgång. Hur ser en förklaring/teori ut?
https://www.youtube.com/watch?v=5ZnKIPfIhAQ&nohtml5=False
/Gabrielle J, Haganässkolan, Osby 2016-04-08
Hej,
under våra fysikspecialiserings lektioner har vi diskuterat teorin bakom detta experiment, utan framgång. Hur ser en förklaring/teori ut?
https://www.youtube.com/watch?v=5ZnKIPfIhAQ&nohtml5=False
/Gabrielle J, Haganässkolan, Osby 2016-04-08
Svar:
Fritt fall med löst rep
För det första: detta är fullständigt livsfarligt om man inte gör det rätt! Rätt utfört är det en utmärkt demonstration av rörelsemängdsmomentets bevarande (se fråga [12527]) och friktion.
För en tyngd med massan m som snurras runt i ett snöre med längden r och med hastigheten v är rörelsemängdsmomentet
L = mvr
(Egentligen är L en vektor, men låt oss inte krångla till det.)
Massan är naturligtvis konstant, så om r minskar måste v öka för att L skall vara konstant. Allteftersom linan med tyngden roterar kring den horisontella stolpen blir ju r mindre. I början glider ju repet mot stolpen, vilket även det gör att r minskar. För att rörelsemängdsmomentet skall bevaras måste alltså tyngdens hastighet öka. Detta innebär två saker som är väsentliga:
1 Tyngden snurrar snabbare och snabbare runt stolpen och många varv runt stolpen hindrar att linan glider.
2 Den ökande hastigheten gör att spänningen i linan ökar (F=mv2/r).
Både 1 och 2 medför att friktionen ökar vilket bromsar upp gubben. Den ökande hastigheten bidrar till att gubben hinner bromsas in innan han slår i marken.
Längden på linan, friktionen mellan rep/stolpe och massan hos vikten måste anpassas så att gubben bromsas upp lagom fort. För mycket uppbromsning gör att gubben dras sönder av linan, för liten uppbromsning och gubben slår i marken.
Här är videon. Man ser att det i princip är fråga om ett bungyjump med översta ändan lös och utan elasticitet i linan.
/Peter E 2016-04-08
Fritt fall med löst rep
För det första: detta är fullständigt livsfarligt om man inte gör det rätt! Rätt utfört är det en utmärkt demonstration av rörelsemängdsmomentets bevarande (se fråga [12527]) och friktion.
För en tyngd med massan m som snurras runt i ett snöre med längden r och med hastigheten v är rörelsemängdsmomentet
L = mvr
(Egentligen är L en vektor, men låt oss inte krångla till det.)
Massan är naturligtvis konstant, så om r minskar måste v öka för att L skall vara konstant. Allteftersom linan med tyngden roterar kring den horisontella stolpen blir ju r mindre. I början glider ju repet mot stolpen, vilket även det gör att r minskar. För att rörelsemängdsmomentet skall bevaras måste alltså tyngdens hastighet öka. Detta innebär två saker som är väsentliga:
1 Tyngden snurrar snabbare och snabbare runt stolpen och många varv runt stolpen hindrar att linan glider.
2 Den ökande hastigheten gör att spänningen i linan ökar (F=mv2/r).
Både 1 och 2 medför att friktionen ökar vilket bromsar upp gubben. Den ökande hastigheten bidrar till att gubben hinner bromsas in innan han slår i marken.
Längden på linan, friktionen mellan rep/stolpe och massan hos vikten måste anpassas så att gubben bromsas upp lagom fort. För mycket uppbromsning gör att gubben dras sönder av linan, för liten uppbromsning och gubben slår i marken.
Här är videon. Man ser att det i princip är fråga om ett bungyjump med översta ändan lös och utan elasticitet i linan.
/Peter E 2016-04-08
Hur kan arbetet som behövs för att ta sig från t.ex. jorden till månen räknas ut?
Fråga:
Hur kan arbetet som behövs för att ta sig från t.ex. jorden till månen räknas ut?
Hur ska arbetet räknas ut om man ska oändligt långt bort från jorden?
/Kalle K, 2016-05-12
Hur kan arbetet som behövs för att ta sig från t.ex. jorden till månen räknas ut?
Hur ska arbetet räknas ut om man ska oändligt långt bort från jorden?
/Kalle K, 2016-05-12
Svar:
Om man bortser från förluster är det lätt.
Kraften på avståndet r från jordens centrum ges av (länk 1):
F = GMm/r2
Om vi integrerar detta får vi potentialen
U(r) = - GMm/r
G är gravitationskonstanten 6.67408×10-11, M är jordens massa m är din massa. Massor och avstånd finns i Planetary Fact Sheets
. Minsta arbetet mellan två punkter ges av differensen mellan respektive potential. Observera att alla värden skall vara i SI enheter. Om r är oändligheten är potentialen 0.
/Peter E 2016-05-13
Om man bortser från förluster är det lätt.
Kraften på avståndet r från jordens centrum ges av (länk 1):
F = GMm/r2
Om vi integrerar detta får vi potentialen
U(r) = - GMm/r
G är gravitationskonstanten 6.67408×10-11, M är jordens massa m är din massa. Massor och avstånd finns i Planetary Fact Sheets
. Minsta arbetet mellan två punkter ges av differensen mellan respektive potential. Observera att alla värden skall vara i SI enheter. Om r är oändligheten är potentialen 0./Peter E 2016-05-13
Rullande kulor och cylindrar
Fråga:
Vad är det som spelar roll för vilken av innebandybollen eller bocciabollen som kommer snabbast ner för en rutschkana?
/Isak K, Europaportens skolor, Malmö 2016-10-14
Vad är det som spelar roll för vilken av innebandybollen eller bocciabollen som kommer snabbast ner för en rutschkana?
/Isak K, Europaportens skolor, Malmö 2016-10-14
Svar:
För ett icke rullande föremål på ett lutande plan omvandlas potentiell energi till rörelseenergi. Om vi kan borse från friktion kommer alla föremål att ha samma hastighet nedför planet:
mgh = mv2/2
v = sqrt(2gh)
Den viktigaste skillnaden om föremålet rullar är relativt tröghetsmoment. (Vi förutsätter att bollarna rullar utan friktionsförluster och glid.) Tröghetsmomentet beror av massfördelningen. Mycket massa nära ytan av bollen och stor radie ger högt tröghetsmoment och därmed mer rotationsenergi för en given rotationshastighet. Denna tas från den vanliga rörelseenergin, vilket saktar ner den linjära rörelsen.
Rullande föremål med högt tröghetsmoment rullar alltså långsammare än föremål med lågt tröghetsmoment. Bocciabollen är homogen av metall (Bocce ). En innebandyboll är ihålig och av plast (Innebandyboll). Massfördelningen skulle ge ett högt tröghetsmoment för innebandybollen och lägre för bocciabollen. Densiteten är emellertid mycket högre för bocciabollen, så jag tror denna rullar saktare. Det hade varit enklare om bollarna varit av samma material och med samma radie.
Se fråga [20352] och [14738] för mer om rullande kulor.
I länk 1 och 2 finns tröghetsmomentet för några olika objekt. Om massan och radien är lika får vi följande för sluthastigheten:
kloss (ingen rotation): sqrt(2gh) = 1.41sqrt(gh)
boll: sqrt((10/7)gh) = 1.20sqrt(gh)
cylinder: sqrt((4/3)gh) = 1.15sqrt(gh)
ring: sqrt(1gh) = 1sqrt(gh)
/Peter E 2016-10-14
För ett icke rullande föremål på ett lutande plan omvandlas potentiell energi till rörelseenergi. Om vi kan borse från friktion kommer alla föremål att ha samma hastighet nedför planet:
mgh = mv2/2
v = sqrt(2gh)
Den viktigaste skillnaden om föremålet rullar är relativt tröghetsmoment. (Vi förutsätter att bollarna rullar utan friktionsförluster och glid.) Tröghetsmomentet beror av massfördelningen. Mycket massa nära ytan av bollen och stor radie ger högt tröghetsmoment och därmed mer rotationsenergi för en given rotationshastighet. Denna tas från den vanliga rörelseenergin, vilket saktar ner den linjära rörelsen.
Rullande föremål med högt tröghetsmoment rullar alltså långsammare än föremål med lågt tröghetsmoment. Bocciabollen är homogen av metall (
). Massfördelningen skulle ge ett högt tröghetsmoment för innebandybollen och lägre för bocciabollen. Densiteten är emellertid mycket högre för bocciabollen, så jag tror denna rullar saktare. Det hade varit enklare om bollarna varit av samma material och med samma radie.Se fråga [20352] och [14738] för mer om rullande kulor.
I länk 1 och 2 finns tröghetsmomentet för några olika objekt. Om massan och radien är lika får vi följande för sluthastigheten:
kloss (ingen rotation): sqrt(2gh) = 1.41sqrt(gh)
boll: sqrt((10/7)gh) = 1.20sqrt(gh)
cylinder: sqrt((4/3)gh) = 1.15sqrt(gh)
ring: sqrt(1gh) = 1sqrt(gh)
/Peter E 2016-10-14
Mörk materia
Fråga:
Hej! Min fråga angår mörk materia.
Om jag förstått det rätt så kan man visualisera "rummet" som kuber och att materia böjer kuberna mot sitt centrum och ger upphov till gravitation. Skulle det vara möjligt att någon händelse eller liknande gjorde att kuberna blev konstant böjda och det är då det som vi ser som mörkmateria?
/Fredrik A, Ingen, Kållered 2016-11-20
Hej! Min fråga angår mörk materia.
Om jag förstått det rätt så kan man visualisera "rummet" som kuber och att materia böjer kuberna mot sitt centrum och ger upphov till gravitation. Skulle det vara möjligt att någon händelse eller liknande gjorde att kuberna blev konstant böjda och det är då det som vi ser som mörkmateria?
/Fredrik A, Ingen, Kållered 2016-11-20
Svar:
Det är korrekt att massa kröker rymden - det är ett grundläggande resultat av den allmänna relativitetsteorin. Det finns teoretiker som har spekulerat att mörk materia inte finns utan bara är en spontan krökning hos rymden, se t.ex.Dark_matterAlternative_theories . Problemet är att man måste ge sig på att modifiera Einsteins ekvationer, och det för med sig nya problem.
I måndags (21/11 2016) sändes ett inslag i Vetenskapens värld om mörk materia, se länk 1. Där förutsägs att man rett ut problemet med den mörka materien inom fem år. Vi kan alltid hoppas.
Se fråga [13626] och [9324] för mer om relativitetsteorin och fråga [20164] och [12396] för mörk materia.
Bilden nedan är från länk 2 med bildtexten:
In this image, dark matter (blue) has become separated from luminous matter (red) in the bullet cluster. Image courtesy of Chandra X-ray Observatory.
Det är korrekt att massa kröker rymden - det är ett grundläggande resultat av den allmänna relativitetsteorin. Det finns teoretiker som har spekulerat att mörk materia inte finns utan bara är en spontan krökning hos rymden, se t.ex.
I måndags (21/11 2016) sändes ett inslag i Vetenskapens värld om mörk materia, se länk 1. Där förutsägs att man rett ut problemet med den mörka materien inom fem år. Vi kan alltid hoppas.
Se fråga [13626] och [9324] för mer om relativitetsteorin och fråga [20164] och [12396] för mörk materia.
Bilden nedan är från länk 2 med bildtexten:
In this image, dark matter (blue) has become separated from luminous matter (red) in the bullet cluster. Image courtesy of Chandra X-ray Observatory.
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.
Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar