Svar:
Det är korrekt att trycket uppstår vid molekylernas kollisioner mot en yta. Anledningen till att trycket är konstant (inom mätbara gränser) är helt enkelt att molekyler är väldigt små så det är fråga om väldigt många molekyler som kolliderar med väggarna varje sekund.

Om medelvärdet av antalet kollisioner per tidsenhet är N_m så ges den relativa spridningen i antalet kollisioner av poissonfördelningen (Poisson_distributionOther_applications_in_science) och blir

1/sqrt(N_m)

Eftersom N_m är mycket stort blir spridningen mycket liten och sannolikheten att få ett avvikande värde på trycket blir försvinnande liten. Se även Kinetic_theoryPressure_and_kinetic_energy.

Om ytan är tillräckligt liten kan man emellertid observera slumpmässigheten. Nedanstående bild från Brownian_motion är en simulering av brownsk rörelse hos en dammpartikel i en gas. I detta fallet ger den slumpmässiga variationen av molekylernas kollisioner med dammpartikeln en slumpmässig förflyttning.

Brownsk rörelse, slumpvandring eller random walk är den slumpmässiga rörelse som främst kan iakttas hos mycket små partiklar som svävar i en fluid (fysikaliskt begrepp som motsvarar vätska eller gas). De första studierna av det som idag kallas Brownsk rörelse företogs av biologen och botanikern Robert Brown 1827; den förste som lyckades förklara fenomenet var Albert Einstein 1905. (Brownsk_rörelse)

Einsteins förklaring av Brownsk rörelse var det första direkta beviset att materia består av atomer.

/Peter E 2012-09-24

Svar:
Dennis! Egentligen svarar vi inte på räkneproblem, men detta var faktiskt riktigt kul, så vi gör ett undantag. Problemet innehåller dels uppdelning av en kraft i komposanter och dels tillämpning av energins bevarande.

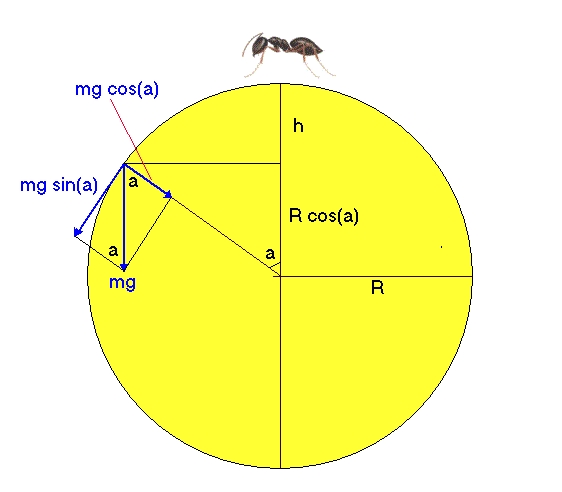
Vi delar upp gravitationskraften mg i en tangentiell komposant, mg sin(a), och en radiell, mg cos(a), se nedanstående bild. Det är alltså den växande tangentiella komposanten som accelererar myran, och den radiella som håller myran kvar på klotet. Så länge myran har kontakt med klotet rör den sig i en cirkelbana med radien R. Efter ett tag kommer den radiella komposanden ha minskat och myrans hastighet v ökat så att myran förlorar kontakten med klotet. För denna punkt gäller

mv²/R = mg cos(a)

dvs

v² = Rg cos(a) (1)

För att beräkna v använder vi förutsättningen att vi inte har någon friktion. Vi kan då använda energiprincipen: den potentiella energin i startpunkten är lika med rörelseenergin i punkten där kontakten med klotet förloras:

mgh = mg(R - R cos(a)) = mv²/2

dvs

v² = 2g(R - R cos(a)) (2)

Om vi sätter in uttrycket för v² från (1) får vi

Rg cos(a) = 2g(R - R cos(a))

cos(a) = 2 - 2 cos(a)

cos(a) = 2/3

vilket är svaret du gav. Vinkeln a är alltså c:a 48 grader.

/fa

/Peter E 2012-12-19

Svar:
Nej. Av olika skäl kan man hävda man åker snabbare om man åker i samma riktning som jorden roterar. Men det primära svaret är: det kvittar.

För det första måste man bestämma sig: i förhållande till vad mäts hastigheten? Det intressanta för ett flygplan är i förhållande till marken. Eftersom atmosfären roterar med resten av jorden (se emellertid nedan) har det ingen som helst betydelse vilken riktning du flyger i.

I förhållande till jordens centrum är emellertid din hastighet högre om du flyger med rotationen - från väster mot öster. Det är därför många satelliter går i banor från väster till öster, se fråga [13636].

Jordens rotation och solens uppvärmning orsakar även s.k. jetströmmar Jetström. Detta är vindar med hastigheter av 90-400 km/t från väster mot öster på en höjd av c:a 10 km (där vanliga jetplan flyger). Dessa vindar är orsaken till att det ofta tar längre tid att flyga från Köpenhamn till New York än att flyga tillbaka mellan New York och Köpenhamn.
/Peter E 2013-01-29

Svar:
Anton/Kalle P! Jag antar att hastigheterna är i förhållande till marken och att bollen kastas mot tåget.

Om tågets massa är mycket stor i förhållande till bollens kommer den relativa hastigheten tåg-boll att bevaras i kollisionen, endast riktningen ändras. Den relativa hastigheten är 10+20=30 m/s. Efter kollisionen rör sig bollen med farten 30 m/s i förhållande till tåget men i tågets riktning. Bollens fart i förhållande till marken är alltså 30+20=50 m/s. Bollens fart har alltså ökat från 10 till 50 m/s genom kollisionen med tåget.

Se fråga [153] och ett liknande problem som har praktisk tillämpning i fråga [12879], [3831] och länk 1.

Bilden nedan är från NASA, länk 1: relativ hastighet är 30+50=80 mph. Bollens hastighet efter stöten blir då 80+50=130 mph.

/Peter E 2013-04-20

Svar:
Hej Tore! Hoppsan! Men det viktiga är inte att proppa i eleverna fakta utan att visa hur man tar reda på hur det är.

Jag kände inte till "gunga tvilling", men som så ofta finns informationen på nätet, länk 1. Det är tydligen helt enkelt att två gungor pendlar i takt. Frågan är om detta fungerar under olika förutsättningar.

Fysikaliskt är en gunga en plan pendel, se fråga [15927]. Se fråga [14065] för härledning av perioden.

Perioden beror alltså bara på g (som förhoppningsvis är konstant 9.81 m/s²) och pendelns längd L. Perioden beror alltså inte på massan. För en gunga som inte är helt en ideal (matematisk) pendel får man approximera pendellängden med avståndet från upphängningspunkten till masscentrum (tyngdpunkten), se fråga [13477].

Så vad säger teorin om dina frågor?

För en tom gunga bör det fungera någotsånär. Masscentrum för den tomma gungan bör vara nära mitten av plankan (eller däcket) man sitter på. Masscentrum med en person ligger lite högre, men inte så att perioden påverkas mycket.

Om personen står upp hamnar masscentrum betydligt högre, dvs L blir mindre och därmed perioden mindre.

Genom att vara aktiv på gungan kan man korrigera små skillnader i period. Så svaret för tom gunga är ja, men om man står upp nja. Det beror helt enkelt hur bra man kan kompensera för gungornas egenfrekvens (enligt formeln: den naturliga perioden, dvs om man sitter still).

Poängen med uppgiften? Tja, en tillämpning av plan pendel och ett tillfälle att träna mätningar. Och framför att diskutera varför resultatet inte alltid blir vad man väntar sig. :-)
/Peter E 2013-12-13

Svar:
En video från kollisionen finns här:

Kenny Bräck survived 214 g's (on his official homepage you can read the following sentences: ...my car caught air at 220 mph, got air borne and smashed straight into a massive steel pole in the catch fence. The impact was enormous, but leaving the cockpit intact. It recorded a record 214 g impact and left me seriously injured...)

Hastigheten vid kollisionsögonblicket är alltså

220 mph = 2201.609 km/t = 2201609/3600 m/s = 98 m/s.

I fråga [10076] visas hur man beräknar accelerationen från hastigheten och deformationszonens längd, x. Låt oss anta att accelerationen 214g är korrekt. Om vi löser ut x får vi

x = v²/(2a) = 98²/(22149.8) = 2.3 m.

Detta är åtminstone av rätt storleksordning. Videon visar att bilen nästan har full hastighet vinkelrätt mot barriären (titta på bromsspåren), så den första kollisionen har haft en mycket hög g-kraft. Bilen fortsatte sedan ner på körbanan där den bromsades upp (roterande) med betydligt mindre g-kraft. En del av bilens rörelseenergi omvandlades alltså till rotationsenergi vid kollisionen.

Bräck hade naturligtvis tur att han klarade sig med livet i behåll. Det var emellertid inte bara tur utan framför allt tack vare bilens konstruktion. Lägg märke till att efter kollisionen återstår i princip en intakt cockpit, allt annat har skalats av och använts som deformationszon och minskat accelerationen.

Se även Kenny_BräckIndy_Racing_League_(andra_andningen).

Under länk 1 finns en kalkylator för att räkna ut accelerationen. Länk 2 med fysik för advokater är ganska kul med bland annat energienheten pund-fot!
/Peter E 2014-02-26

Svar:
Ulrika! Ja, det är korrekt!

Massorna är 2m och m

Hastigheterna är 2v och -v

Bilarnas gemensamma hastighet efter kollisionen är V

Rörelsemängdens (massanhastigheten) bevarande ger

2m2v - mv = (2m+m)V

4mv - mv = 3mV

V = v

Ändringen i hastighet för bil A är alltså v medan den för bil B är 2v. Accelerationen är som framgår av fråga [10076] proportionell mot hastighetsändringen i kvadrat. Accelerationen för bil B är alltså 4 gånger accelerationen av bil A.

Om bil A haft samma hastighet som bil B får vi

2mv - mv = (2m+m)V

mv = 3mV

V = v/3

Hastighetsändringen blir alltså 2v/3 för bil A och 4v/3 för bil B. Accelerationen är alltså fortfarande en faktor 4 större för bil B. Man kan alltså förvänta sig mindre skador om man färdas i en stor bil.

Kraft och motkraft är lika (Newtons tredje lag, se fråga [15642]).
/Peter E 2014-04-09

Svar:
Detta till synes enkla problem är i själva verket ganska komplext. Det är relaterat till stabiliteten hos båtar, se länk 1 och 2 nedan. Jag skall försöka göra en kvalitativ analys av problemet.

Vid jämvikt påverkas plankan av två lika stora och motriktade krafter: tyngdkraften nedåt och lyftkraften uppåt. Dessa krafter har angreppspunkter i tyngdpunkten (masscentrum) respektive lyftkraftscentrum.

Vi börjar med figur A och C nedan. Enda skillnaden är att den del av plankan som är över vattenytan i medeltal är högre upp i fall C. Den potentiella energin är alltså högre i C än i A. Tillståndet med lägst energi är det mest stabila. Detta förklarar varför A (den liggande plankan) är mest stabil.

Om man lutar plankan lite grann kommer lyftkraftscentrum att förskjutas i sidled, och de verkande krafterna ger upphov till ett vridande moment. Observera att detta vridmoment är riktat så att lutningen minskas, dvs det är stabiliserande. Om vi nu jämför fall B och D, så finner vi att vridmomentet i B är betydligt större än i D eftersom krafternas angreppspunkter ligger längre ifrån varandra i B. Vi ser alltså att jämviktsläget med liggande planka (fall A) är mer stabilt än det i fall C.

/Peter E 2014-04-11

Svar:
Först måste du räkna ut tyngdaccelerationen på månen. Enligt
fråga [16455] ges månens tyngdacceleration av

g_månen = (M G)/R²

Månens massa M och radie R finns på länk 1. Gravitationskonstanten G är 6.67384×10^-11 m³ kg^-1 s^-2.

g_månen = (0.0734210²⁴ 6.6738410^-11)/(1737.110³)² =
1.62 m/s²

Förhållandet

g_jorden/g_månen = 9.81/1.62 = 6.06

Eriks tyngd på jorden

6.06100 = 606 N

och hans vikt (massa, se fråga [16048]) är

606/9.81 = 61.8 kg

oberoende var han befinner sig.
/Peter E 2014-11-21

Svar:
För en cirkulär bana med radien r är centripetalkraften
mv²/r. Om vi sätter detta lika med gravitationskraften får vi

mv²/r = GmM/r²

v² = GM/r

v = (GM/r)^1/2

Gravitationskonstanden G är 6.67410^-11 (Gravitational_constant). Övriga data från Planetary Fact Sheets:

Jordens massa: 5.973610²⁴ kg

Jordradien: 6.37110⁶ m


Hastigheten för en cirkelbana vid jordytan blir då

v = (6.67410^-115.973610²⁴/6.37110⁶)^1/2 = 7911 m/s = 7.911 km/s.

Omloppstiden blir

2pr/v = 2p6.37110⁶/7911 = 5060 s = 84.33 minuter.

Se fråga [18350] för alternativa lösningar.
/Peter E 2014-12-10