Svar:
Niclas! Det finns mycket diskussion om nytta eller inte nytta med kväve i däck, se t.ex. länk 1 nedan, Eftersom luft är nära 80% kväve är det klart att effekten av att fylla däcken med kväve i stället för luft är mycket marginell. Det låter alltså för den vanlige bilföraren som en bluff för att lura pengar av oss - tänk att till höga priser kunna sälja i stort sett luft!

För vissa speciella tillämpningar kan det nog ha en liten betydelse, t.ex. för ett flygplansdäck som blir överhettat. Man kan även tänka sig att gummit med tiden oxideras av syret och därmed blir sprött. Jag tror emellertid att mönstret slits ut innan man märker av effekten av oxidation.

Att syret skulle läcka ut snabbare måste vara en liten effekt. Syremolekylen är visserligen lite mindre än kvävemolekylen (eftersom samma skal fylls och kärnladdningen är högre för syre). Detta motverkas av att diffusionshastigheten är högre för en lättare molekyl (kväve). Skulle man se någon effekt i lufttrycket så måste hälften av syret läcka ut, och det tror jag inte på. Dessutom kontrollerar väl varje bilförare däcktrycket regelbundet :-)!

Att kvävet skulle ha något med tryckökningen när temperaturen blir högre är också nonsens. Från allmänna gaslagen kan man härleda (se fråga [15619])

Dp/p = DT/T

Alltså den relativa tryckändringen beror endast av temperaturer, inte av vilken gas man har! Det är emellertid sant som du säger att man använder kvävgas till däcken i tävlingsbilar. Det kan knappast vara läckage (däcken på en Formel 1 bil varar högst någon timme). Knappast oxidation heller. Möjligen lite säkrare vid brand, men Formel 1 bilar brinner sällan i dag. Förklaringen ges i länk 2.

Kvävet innehåller alltså ingen vattenånga eftersom det framställs genom att kyla ner luft tills kvävet kondenseras till vätska, och vattnet fryser bort på ett tidigt stadium. Vatten ställer till det i däcket eftersom det kan kondensera till vätska vid låg temperatur, men blir ånga vid hög temperatur. Vid hög temperatur har vi alltså fler molekyler (luft+vattenånga) och därmed högre tryck. Gaslagen säger ju

pV = nRT,

så om antalet mol n ökar så ökar trycket. Man kan se det så att eftersom n ökar med temperaturen (fler molekyler i gasfas) blir sambandet p-T olinjärt.

Användandet av kväve är alltså ett villospår, och det är som du föreslår vatteninnehållet som är det viktiga. Man kan lika gärna använda luft så länge den inte innehåller något vatten. Tydligen är det emellertid enklare att framställa kvävgas än torr luft!
/Peter E 2011-02-23

Svar:
Fredrik! Jag tycker du skall hålla fast vid bilden av en luftpelare. Samma bild fungerar även bra om du dyker under vattenytan: övertrycket ges av tyngden av vattenpelaren per ytenhet.

Kraften som verkar på varje ytenhet är densamma oberoende av ytans riktning. Detta gäller gaser och vätskor som inte har en bestämd form. Om du sänker ner ett föremål i vatten kommer du att få ett lite högre tryck på undersidan än på översidan. Denna lyftkraft är lyftkraften i Arkimedes princip, se [13509]. Lyftkraften beror alltså på skillnaden i vätskepelare från undersidan och översidan.

Man kan faktiskt beräkna atmosfärens totala massa m_atm från lufttrycket p

p = F/A = m_atmg/A

där g är tyngdaccelerationen och A är jordens yta. Om jordens radie är R får vi

A = 4p R²

och alltså

m_atm = p4p R²/g.

Om vi tar medelvärdet på g till 9.81 m/s², medeltrycket till 0.98610⁵ Pa ) och jordens radie R till 6371 km får vi

m_atm = 0.98610⁵4p (6.37110⁶)²/9.81 = 5.1310¹⁸ kg

vilket stämmer bra med det accepterade värdet (Atmosphere_of_EarthDensity_and_mass).
___________________________________________________________

) Detta är lite lägre än medeltrycket vid havsytan 1.01310⁵ eftersom man måste ta hänsyn till berg och höjdplatåer.
/Peter E 2011-09-07

Svar:
En varmluftsballong är ju öppen dertill så att flamman kan värma luften inne i ballongen, se nedanstående bild från Wikimedia Commons. Detta betyder att lufttrycket är samma inne i ballongen som utanför. I fråga [7692] visas från den allmänna gaslagen att densiteten hos luften ges av

r = konst/T

Vi ser alltså att densiteten blir mindre med ökande absolut temperatur T. Eftersom lufttemperaturen är högre inne i ballongen än utanför blir densiteten mindre och vi får en lyftkraft.

Lyftkraften hos en varmluftsballong beräknas i fråga [14826].

Se vidare Hot_air_balloon.

Det är korrekt att trycket i en heliumfylld gummiballong är högre än det omgivande lufttrycket. Differensen tas upp av elastisiteten i gummimaterialet. I fråga [15377] beräknas lyftkraften hos en heliumballong.

Man skall alltså skilja på en varmluftsballong, där den lägre densiteten orakas av högre temperatur, och en heliumballong, där den lägre densiteten orsakas av heliumgasens lägre molekylvikt.

Se även fråga [18443].

/Peter E 2011-10-10

Svar:
a (kg/m³)m²(m/s)² = kgm/s² = N, vilket är SI enheten för kraft.

b Sluthastigheten uppnås när luftmotståndet är lika med tyngdkraften mg:

mg = k r²v²

v² = mg/(k r²) = 0.00259.81/(0.92(0.019)²) = 73.8

v = sqrt(73.8) = 8.6 m/s

Låter lite mycket, men nog korrekt med de givna uppgifterna!

Låt oss kontrollera med uttrycket för sluthastighet som finns i fråga [15385] (med luftens densitet 1.2 kg/m³):

v = sqrt(2mg/(rAC_d)) =
sqrt(20.00259.81/(1.2p(0.019)²0.47)) = 8.8 m/s

vilket stämmer utmärkt med ovanstående värde!
/Peter E 2011-10-13

Svar:
Det finns flera sätt att härleda den erforderliga hastigheten för en satellitbana nära jordytan. Låt oss börja med den mest direkta metoden, se figuren nedan. Om hastigheten för en låg cirkelbana är v så är sträckan mot horisonten på en sekund lika med v1 m. Under en sekund faller föremålet med accelerationen g sträckan

gt²/2 = 9.81/2 m

Jordens radie är r=6.3710⁶ m (Planetary Fact Sheets). I figuren har vi två likformiga trianglar (observera att a är mycket liten så jordens krökning och skillnaden mellan katet och hypotenusa är försumbar):

(9.81/2)/v = (v/2)/r

v² = 9.81r = 9.816.3710⁶ = 62.510⁶

v = 7.9110³ m/s = 7.91 km/s

Man kan även härleda hastigheten från Keplers tredje lag, se fråga [12644]

P² = 4p²a³/(GM)

För en cirkelbana är halva storaxeln a lika med radien r. Om man tar G från fråga [12644] och M från Planetary Fact Sheets, får man

P² = 4p²(6.3710⁶)³/(6.67310^-115.9710²⁴) = 25.610⁶

och

P = 5050 s = 84.2 minuter (omloppstid)

Banhastigheten v blir

v = s/t = 2pr/5050 = 7.9210³ m/s = 7.92 km/s

i god överensstämmelse med värdet ovan.

Länk 1 har en lättillgänglig och trevlig animering av problemet. Länk 2 förklarar relativt ingående. Se även OrbitUnderstanding_orbits och fråga [463].

Se fråga [19564] för en alternativ lösning.

/Peter E 2011-11-30

Svar:
Maria! Bra idé att utnyttja barnens naturliga nyfikenhet! Det viktiga till att börja med är att utföra enkla experiment och försöka se samband. Fysikaliska lagar är ofta matematiska och teoretiska, och lämpar sig kanske inte för de yngsta. Dessutom kan vi fysiker aldrig svara på frågan varför? som barnen ofta ställer. Däremot kan man genom experiment och observationer se samband och beskriva hur?.

Länk 1 nedan ger lite tips om Lekplatsfysik och i länk 2 finns inbjudan till några Facebook-grupper modererade av Nationellt ResursCentrum för Fysik.

Just Newtons rörelselagar är ganska teoretiska och kanske lite svåra att realisera, se nedan. Att alla föremål faller lika fort (fritt fall och lutande plan) är ett enkelt faktum som också är svårt att visa eftersom luftmotstånd och friktion påverkar resultatet. Här är en demonstration som inte är helt enkelt att utföra: [13663].

En pendel (gunga) är relativt lätt att experimentera med, se fråga [14065]. Man kan t.ex. kontrollera att perioden är oberoende av massan och hur perioden beror av pendelns längd.

Här är några frågor som behandlar vad fysik är och lite tips om vad man kan göra: [17691], [15609], [15378] och [12126].

Newtons tre rörelselagar

1 En kropp förblir i vila eller i likformig rörelse så länge inga yttre krafter verkar på kroppen

Många tror att det behövs en kraft för att ett föremål skall röra sig. Stannar man motorn på en bil så stannar ju bilen efter ett tag. Men detta beror på att det finns bromsande krafter: luftmotstånd och friktion.

2 F = ma

Detta är definitionen av kraft, F. Accelerationen a är proportionell mot kraften. Massan m är proportionalitetskonstanten.

3 Två kroppar, A och B, påverkar alltid varandra med lika stora men motriktade krafter

Denna lag kan vara svår att tolka. Man ritar in två motriktade krafter och tycker att eftersom de är motriktade och lika stora så tar de ut varandra. Men vad lagen säger är att A påverkar B med samma kraft som B påverkar A. A påverkas alltså av en kraft, kraften från B. Den moderna formuleringen på den tredje lagen är att i ett slutet system bevaras rörelsemängden (massahastighet, mv).

Som synes är det inte helt lätt att göra förståeliga experiment på Newtons rörelselagar. Men det finns massor av enklare experiment: Arkimedes princip (vad flyter), optik (reflektion, brytning), ljud (musikinstrument), färger (blandning av färger). På sidan under länk 1 finns några enkla mekanikexperiment.
/Peter E 2011-12-20

Svar:
Intressant fråga, så jag testade det genom ett litet experiment i vad som på engelska kallas "kitchen sink physics".

En möjlig förklaring är att vattnet faller fritt när det lämnar kranen. När hastigheten ökar måste därför strålens diameter minska för att vattnets volym skall bevaras. Vi använder formlerna för fallrörelse med konstant acceleration.

I figuren nedan syns att vattenstrålen definitivt bli tunnare allteftersom den rör sig nedåt.

Låt oss börja med några allmänna uttryck för likformig acceleration (konstant acceleration, t.ex. i tyngdkraftfältet), se AccelerationUniform_acceleration. Man brukar använda följande beteckningar för storheterna:

v sluthastighet (vid tiden t, m/s)

u begynnelsehastighet (vid tiden 0, m/s)

s sträcka (m)

a acceleration (m/s²)

t tid (s)

Acceleration definieras som (ändring i hastighet)/(tiden) dvs

a = (v-u)/t

Genom omgruppering får vi

v = u + at (1)

Medelhastigheten ges av

(u+v)/2 = s/t

vilket kan omgrupperas till

s = [(u + v)/2] t (2)

Vi använder (1) för att eliminera v från ekvation (2)

s = ut + at²/2 (3)

Slutligen använder vi (1) för att eliminera t i ekvation (2)

s = [(v+u)/2][(v-u)/a] = (v² - u²)/2a

vilket ger uttrycket

v² = u² + 2as (4)

VI kommer att använda ekvation (4) för att testa "fritt fall"-hypotesen.

Vi behöver först bestämma vattenflödet F. Vi gör detta genom att mäta tiden det tar att fylla ett enliters kärl. Det tog 90 sekunder, så flödet blir:

F = 1 [l]/90 [s] = 110^-3 [m³]/90 [s] = 1.1110^-5 m³/s

Genom att mäta diametern hos den grå adaptern (33 mm) kunde en kalibrering för mm/pixel på bilden åstadkommas (originalet är 4 gånger större än nedanstående bild). Därefter kunde alla avstånd mätas och omräknas till mm.

I tabellen nedan finns alla uppmätta och uträknade data: avstånd från startpunkten, strålens radie, hastigheten, fritt fall hastighet och differensen i hastighet.

____________________________________________________





D (mm) r (mm) v (m/s) vB (m/s) Differens (%)

 0 3.21 0.34 50 1.77 1.12 1.05 -6%

 94 1.47 1.62 1.45 -10%

____________________________________________________

Bevarande av flödet ger följande samband:

Av = p r²v = F

dvs

v = F/(p r²)

A är tvärsnittsytan, v är hastigheten och r är strålens radie.

För positionen D = 0 får vi t.ex.

v = 1.1110^-5/(p(3.2110^-3)²) = 0.34 m/s

Med hjälp av ekvation (4) ovan kan vi få ett beräknat värde på hastigheten om hypotesen fritt fall är korrekt:

v_B = sqrt(0.34² + 2g5010^-3) = sqrt(0.116 + 0.981) = 1.05 m/s

och

v_B = sqrt(1.12² + 2g4410^-3) = sqrt(1.25 + 0.86) = 1.45 m/s

Avvikelsen mellan de uppmätta värdena på hastigheterna och de som beräknats för fritt fall är -6% och -10%. Det är nog lite för stora avvikelser för att helt kunna förklaras som tillfälliga mätfel. Det tycks alltså komma in andra effekter, t.ex. ytspänning och laminär strömning, dvs att hastigheten inte är konstant över tvärsnittsytan, se Laminar_flow. Den svenska Wikipedia artikeln Laminär_strömning är ganska intetsägande, men innehåller ett kul skämt :-) (bildtexten till bilden med fiskar).

I länk 1 beskrivs ett liknande experiment. Man använder sig av Bernoullis ekvation, som emellertid ger exakt samma resultat som i ekvation (4). Länk 2 behandlar acceleration och fritt fall (v-t diagram).

____________________________________________________________________

För att undvika lokala effekter från kranen valdes nollpunkten en bit ner. Nedre punkten valdes lite ovanför 100 mm nivån eftersom bilden av strålen blir ganska otydlig.

/Peter E 2012-01-19

Svar:
Jonas! Att evighetsmaskiner inte fungerar vet de flesta eftersom de strider mot termodynamikens lagar, se fråga [15733]. Konstruktioner för evighetsmaskiner är emellertid ofta mycket komplicerade, så det kan vara mycket svårt att genomskåda dem. I detta fallet är det emellertid inte så svårt att se var resonemanget går fel.

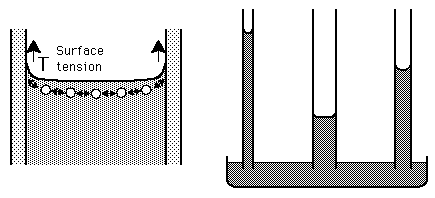
Titta på figuren nedan (från fråga [596]). Kapillärkraften orsakas av assymmetrin hos begränsningsytan rör-vätska. Om man, som för glas-vatten, har en konkav yta (sett utifrån) så orsakar krökningen en uppåtriktad kraft. Det är denna som får vattnet att stiga olika högt beroende på rörets diameter. Det är alltså bara ytan som ger en kraft, längs resten av röret råder fullständing symmetri uppåt-nedåt.

Vad skulle hända om vi sågade av det tunnaste röret nedanför vattenytan? Jo vattnet skulle stiga till toppen på röret och krökningen hos vattenytan skulle minska precis så mycket att kapillärkraften motsvarar den nya längden på vattenpelaren. Det rinner alltså inte ut något vatten. Det samma gäller om man kröker röret så att slutet pekar nedåt. Ytspänningen kommer att verka uppåt och hindra vattnet från att rinna ut, se Perpetual_motionGallery.

Man kan alltså inte transportera vatten enbart med kapillärkraften, se fråga [9033]. Träd transporterar vattnet genom att först med osmos och kapillärkraft skapa en vattenpelare. Vattnet pumpas sedan upp genom att det skapas ett undertryck genom att vattenånga bildas och går ut genom bladens klyvöppningar. Det är alltså värmen från solen som är "motorn" i systemet.

/Peter E 2012-03-01

Svar:
David! Om en elektriskt laddad kropp accelereras sänds det ut elektromagnetisk strålning. Denna kallas ofta för bromsstrålning.

En kropp med massa (t.ex. en planet som går runt solen) som accelereras sänder ut gravitationsstrålning. Denna innehåller energi, så systemet förlorar energi. För "normala" system som planetsystem och galaxer är emellertid den utsända effekten mycket liten. Effekten ges av uttrycket i Gravitational_radiationPower_radiated_by_orbiting_bodies, se bilden nedan. Observera att den lilla gravitationskonstanten finns som G⁴ i täljaren och den stora ljushastigheten som c⁵ i nämnaren. Det är detta som gör effekten så liten.

Jorden förlorar mycket riktigt energi genom gravitationsstrålning och närmar sig därmed solen, men effekten är helt försumbar. Man får gå till mycket speciella system, som dubbelpulsarer och svarta hål, för att kunna observera en effekt. Se vidare fråga [473].

/fa

/Peter E 2012-05-07

Svar:
Karl! Nej, det du säger är korrekt, men du glömmer en sak: den potentiella energin i begynnelsetillståndet. När kropparna faller mot varandra omvandlas den potentiella (gravitations)energin till rörelseenergi. Denna rörelseenergi blir till värme vid kollisionen. Sett utifrån har ännu inget hänt - systemets massa är fortfarande 2m. Värmen kommer med tiden att stråla bort i form av temperaturstrålning. Massan blir då lite mindre än 2m. Det är alltså den potentiella energin i begynnelsetillståndet som omvandlas till rörelseenergi och till slut till värme som sedan strålar bort.

Karl kom med en följdfråga:

Jag tänker att man istället kan se pot energi (eller avsaknaden av det) som en form av massdefekt, skapad i samspel med gravitationen.

Ja det kan man. Det är bara två sätt att uttrycka samma sak. Den potentiella energin är av konvention noll när kropparna befinner sig på stort avstånd från varandra. När de faller mot varandra ökar rörelseenergin i samma mån som potentiella energin minskar. Den potentiella energin är då alltså negativ eftersom den började på noll. Den energi som behövs för att separera kropparna från ett visst avstånd är absolutbeloppet av den negativa potentiella energin. Denna kallas separationenergi.

Massdefekt (se fråga [1433]) används normalt bara för atomkärnor. Anledningen är att den för klassiska system är försumbar, medan den för atomkärnor är relativt stor. Låt oss se vad massdefekten är för ⁴He. Denna kärna är sammansatt av två ¹H och två neutroner.

Beståndsdelarna har massan (se länk 1)

(21.008665+21.007825) = 4.032980 u (atommassenheter)

⁴He har massan

4.002603 u

Differensen blir

4.032980 - 4.002603 = 0.030377 u = 931.50.030377 MeV = 28.296 MeV

där massdefekten uttryckt i MeV brukar kallas bindningsenergi. Vi kan se att massdefekten i detta fallet utgör

1000.030377/4 = 0.76 % av massan av ⁴He.
/Peter E 2012-05-15