Vill du ha ett snabbt svar - sök i databasen
600 frågor / svar hittades
Berg-och-dal bana med loop
Fråga:
Frågan gäller en berg-och-dal bana med en loop.
Hur stor är centripetalaccelerationen längst upp på karusellen? Var är centripetalaccelerationen som störst?
/Ali z, BORGARSKOLAN, MALMÖ 2009-11-05
Frågan gäller en berg-och-dal bana med en loop.
Hur stor är centripetalaccelerationen längst upp på karusellen? Var är centripetalaccelerationen som störst?
/Ali z, BORGARSKOLAN, MALMÖ 2009-11-05
Svar:
Ali! Jag hade lite svårt att förstå din fråga. Det du frågar om är nog en berg-och-dalbana (Roller_coaster , Roller_coaster_elements ) med en loop (Vertical_loop ), se nedanstående foto av den första loopen (Coney Island, New York) från Wikimedia Commons. Jag har kortat ner din fråga något.
Jag tänkte ta upp ett par saker av vad jag tror du frågade om: hur räknar man ut vagnens hastighet i olika punkter och hur stora är g-krafterna? Sajten Lisebergs-Fysik innehåller mycket mer information bland annat om berg-och-dal banor.
innehåller mycket mer information bland annat om berg-och-dal banor.
För att få någon idé om storlekar, hastigheter etc, så har jag tittat på data från ett typexempel, länk 1.
En klassisk berg-och-dal bana fungerar så att vagnen dras upp till maxhöjden, och får sedan rulla i princip fritt ner och upp längs spåret. En förenklad version visas i figuren nedan. Vagnen startar med hastigheten 0 från punkt 1. Den accelereras nedför backen och går runt loopen. I verkligheten är naturligtvis loopen lite skruvad så att utgången är vid sidan av ingången.
Om vi antar att det inte finns några friktionsförluster kan vi använda energiprincipen för att räkna ut hastigheten i olika punkter: Totala energin = potentiell energi + kinetisk energi, Epot + Ekin = konstant.
Vagnens massa är M kg och vi räknar med tyngdaccelerationen g=10 m/s2. Radien på loopen är r=5 m.
I tabellen nedan listas värden för punkterna 1-4. De olika kolumnerna är:
Nr Punkt nummer
h Höjd över nollnivån (lägsta nivån [punkt 2] har h=0)
Epot Potentiell energi: Mgh
Ekin = 160M - Epot
v2 räknas ut från Ekin = Mv2/2
v räknas ut från v2
v2/r är centripetalaccelerationen i cirkelbanan i m/s2
C acc är centripetalaccelerationen uttryckt i g
Totalt g är totala g-kraften om vi även tar tyngdaccelerationen i beaktande, se vektordiagrammen längst ner i figuren. I stället för att involvera krafter är det i detta fallet enklare att räkna med accelerationer. Tyngkraften motsvaras då av en acceleration riktad rakt upp med beloppet 1g (de små svarta pilarna i figuren).
Vi kan räkna ut vad starthöjden skulle vara om centripetalaccelerationen i punkt 4 skulle vara g, dvs passagerarana skulle vara tyngdlösa:
v2/r = 10 -> v2 = 105 = 50
Ekin = Mv2/2 = M50/2 = 25M
Potentiella energin 25M motsvarar höjden 2.5 m, så starthöjden behöver vara 12.5 m för att centripetalaccelerationen i punkt 4 precis skall kompensera tyngaccelerationen.
Kommentarer
1 Maximala g-kraften i detta exemplet är 7.4 (i punkt 2) medan det i länk 1 sägs att den maximala g-kraften är 4. Ett skäl till avvikelsen kan vara att loopen inte vilar på lägsta nivån eller har större radie. Ett annat skäl är att man gör inte loopen cirkulär, utan päronformad med tjocka änden nedåt. Man får då en större krökningsradie där vagnen rör sig snabbast, och en mindre radie där den rör sig långsammast. Man jämnar alltså ut g-kraftena i loopen.
2 Det kan tyckas farligt att vagnen är upp-och-ner i toppen av loopen. I moderna anläggningar (men inte i den avbildade nedan) har man dubbla skenor både över och under hjulen. Om alltså vagnen skulle tappa fart så att den inte går tillräckligt snabbt på toppen, så skulle den ändå hänga kvar i de extra skenorna.
Se även Berg-_och_dalbana .
.
Ali! Jag hade lite svårt att förstå din fråga. Det du frågar om är nog en berg-och-dalbana (
Jag tänkte ta upp ett par saker av vad jag tror du frågade om: hur räknar man ut vagnens hastighet i olika punkter och hur stora är g-krafterna? Sajten Lisebergs-Fysik
För att få någon idé om storlekar, hastigheter etc, så har jag tittat på data från ett typexempel, länk 1.
En klassisk berg-och-dal bana fungerar så att vagnen dras upp till maxhöjden, och får sedan rulla i princip fritt ner och upp längs spåret. En förenklad version visas i figuren nedan. Vagnen startar med hastigheten 0 från punkt 1. Den accelereras nedför backen och går runt loopen. I verkligheten är naturligtvis loopen lite skruvad så att utgången är vid sidan av ingången.
Om vi antar att det inte finns några friktionsförluster kan vi använda energiprincipen för att räkna ut hastigheten i olika punkter: Totala energin = potentiell energi + kinetisk energi, Epot + Ekin = konstant.
Vagnens massa är M kg och vi räknar med tyngdaccelerationen g=10 m/s2. Radien på loopen är r=5 m.
I tabellen nedan listas värden för punkterna 1-4. De olika kolumnerna är:
Nr Punkt nummer
h Höjd över nollnivån (lägsta nivån [punkt 2] har h=0)
Epot Potentiell energi: Mgh
Ekin = 160M - Epot
v2 räknas ut från Ekin = Mv2/2
v räknas ut från v2
v2/r är centripetalaccelerationen i cirkelbanan i m/s2
C acc är centripetalaccelerationen uttryckt i g
Totalt g är totala g-kraften om vi även tar tyngdaccelerationen i beaktande, se vektordiagrammen längst ner i figuren. I stället för att involvera krafter är det i detta fallet enklare att räkna med accelerationer. Tyngkraften motsvaras då av en acceleration riktad rakt upp med beloppet 1g (de små svarta pilarna i figuren).
Nr h Epot Ekin v2 v v2/r C acc Totalt g
1 16 160M 0 0 0
2 0 0 160M 320 18 64 6.4 7.4
3 5 50M 110M 220 15 44 4.4 4.5
4 10 100M 60M 120 11 24 2.4 1.4
m J J (m/s)2 m/s m/s2
Vi kan räkna ut vad starthöjden skulle vara om centripetalaccelerationen i punkt 4 skulle vara g, dvs passagerarana skulle vara tyngdlösa:
v2/r = 10 -> v2 = 105 = 50
Ekin = Mv2/2 = M50/2 = 25M
Potentiella energin 25M motsvarar höjden 2.5 m, så starthöjden behöver vara 12.5 m för att centripetalaccelerationen i punkt 4 precis skall kompensera tyngaccelerationen.
Kommentarer
1 Maximala g-kraften i detta exemplet är 7.4 (i punkt 2) medan det i länk 1 sägs att den maximala g-kraften är 4. Ett skäl till avvikelsen kan vara att loopen inte vilar på lägsta nivån eller har större radie. Ett annat skäl är att man gör inte loopen cirkulär, utan päronformad med tjocka änden nedåt. Man får då en större krökningsradie där vagnen rör sig snabbast, och en mindre radie där den rör sig långsammast. Man jämnar alltså ut g-kraftena i loopen.
2 Det kan tyckas farligt att vagnen är upp-och-ner i toppen av loopen. I moderna anläggningar (men inte i den avbildade nedan) har man dubbla skenor både över och under hjulen. Om alltså vagnen skulle tappa fart så att den inte går tillräckligt snabbt på toppen, så skulle den ändå hänga kvar i de extra skenorna.
Se även Berg-_och_dalbana
 .
.
Länkar: http://www.rcdb.com/181.htm
/Peter E 2009-11-06
Vad kostar det i bränsle att öka hastigheten för en lastbil från 60 till 80 km/tim?
Fråga:
Jag skall hålla en utbildning för lastbilschaufförer. Hastigheten och förmågan att planera sin körning är alltid ett hett ämne som kräver konkreta svar.
Fråga: Vad kostar det i energi (diesel) att öka hastigheten från 60 till 80 km/tim resp från 5 till 25/km/tim. Fordonets totalvikt 60 ton resp 20 ton.
Konsekvens: Om man bromsar från 80 till 60 km/tim förlorar man i princip lika mycket i rörelseenergi som det kostat att accelera från 60 till 80 km/tim.
/Klas G, Brantevik 2009-11-09
Jag skall hålla en utbildning för lastbilschaufförer. Hastigheten och förmågan att planera sin körning är alltid ett hett ämne som kräver konkreta svar.
Fråga: Vad kostar det i energi (diesel) att öka hastigheten från 60 till 80 km/tim resp från 5 till 25/km/tim. Fordonets totalvikt 60 ton resp 20 ton.
Konsekvens: Om man bromsar från 80 till 60 km/tim förlorar man i princip lika mycket i rörelseenergi som det kostat att accelera från 60 till 80 km/tim.
/Klas G, Brantevik 2009-11-09
Svar:
Klas! Eftersom man normalt kör ganska långa sträckor så är det inte accelerationerna som är avgörande utan friktionsförluster - inklusive luftmotstånd. En personbil har en optimal hastighet på c:a 70-90 km/t, se länk 1 och 2 nedan. I länk 1 finns ett diagram på bränsleeffektivitet och tips för effektiv körning.
Om hastigheten är v så är luftmotståndet (bromsande kraften)
Fluftmotstånd = konstantv2
(seDrag_(physics) ). Effekten går som Fv, så förlusterna från luftmotståndet går som v3. Å andra sidan kör man längre per tidsenhet, så slutresultatet blir att effektiviteten minskar som v2.
Det är klart att det optimala är att köra med så konstant hastighet som möjligt. Om man inte har KERS (se fråga 16552 nedan) så är ju bromseffekten rena förluster.
Eftersom rörelseenergin är mv2/2, kostar det mycket mer energi att accelerera från 60 km/t till 80 km/t än att accelerera från 5 km/t till 25 km/t. Kraften som krävs för accelerationen är (bortsett från luftmotståndet) densamma, men kraften verkar vid den högre hastigheten på en längre sträcka, så den erfordrade energin blir större.
Bränsleekonomi för en bil är ett ganska komplicerat ämne med många parametrar, så man kan inte räkna ut bränsleförbrukningen med hjälp av en enkel formel. Det bästa är att pröva själv - vissa bilar visar den ögonblickliga bränsleförbrukningen så för dessa är det enkelt.
Låt oss avslutningsvis beräkna hur mycket diesel det kostar att accelerera en 20 tons lastbil från 5 till 25 km/t och från 60 till 80 km/t. Energiutbytet för dieselolja är enligtEnergy_content_of_biofuel 40.3 MJ/l. Om vi räknar med en effektivitet på 40% blir energiutbytet 16100 kJ/l. Detta värde har använts för att räkna ut förbrukningen i den sista kolumnen.
Det tar alltså hisnande 0.13 l diesel att accelerera vår 20 tons lastbil från 60 till 80 km/t!
/Peter E 2009-11-09
Klas! Eftersom man normalt kör ganska långa sträckor så är det inte accelerationerna som är avgörande utan friktionsförluster - inklusive luftmotstånd. En personbil har en optimal hastighet på c:a 70-90 km/t, se länk 1 och 2 nedan. I länk 1 finns ett diagram på bränsleeffektivitet och tips för effektiv körning.
Om hastigheten är v så är luftmotståndet (bromsande kraften)
Fluftmotstånd = konstantv2
(se
Det är klart att det optimala är att köra med så konstant hastighet som möjligt. Om man inte har KERS (se fråga 16552 nedan) så är ju bromseffekten rena förluster.
Eftersom rörelseenergin är mv2/2, kostar det mycket mer energi att accelerera från 60 km/t till 80 km/t än att accelerera från 5 km/t till 25 km/t. Kraften som krävs för accelerationen är (bortsett från luftmotståndet) densamma, men kraften verkar vid den högre hastigheten på en längre sträcka, så den erfordrade energin blir större.
Bränsleekonomi för en bil är ett ganska komplicerat ämne med många parametrar, så man kan inte räkna ut bränsleförbrukningen med hjälp av en enkel formel. Det bästa är att pröva själv - vissa bilar visar den ögonblickliga bränsleförbrukningen så för dessa är det enkelt.
Låt oss avslutningsvis beräkna hur mycket diesel det kostar att accelerera en 20 tons lastbil från 5 till 25 km/t och från 60 till 80 km/t. Energiutbytet för dieselolja är enligt
Hastighet Ekin DEkin Förbrukning
5 1.4 19.6
25 6.9 476 456.4 0.028
.
60 16.7 2790 80 22.2 4930 2140 0.13
km/t m/s kJ kJ liter dieselolja
Det tar alltså hisnande 0.13 l diesel att accelerera vår 20 tons lastbil från 60 till 80 km/t!
/Peter E 2009-11-09
Har man observerat gravitationsvågor?
Fråga:
Hej, jag har förstått att LIGO är ett projekt med syftet att detektera gravitationsvågor, men när blir en observation lyckad? Vad är det exakt man vill ska hända som man sedan kan använda som ett bevis för gravitationsvågorna?
/Linda J, Jensen, Göteborg 2010-01-20
Hej, jag har förstått att LIGO är ett projekt med syftet att detektera gravitationsvågor, men när blir en observation lyckad? Vad är det exakt man vill ska hända som man sedan kan använda som ett bevis för gravitationsvågorna?
/Linda J, Jensen, Göteborg 2010-01-20
Svar:
Linda! Mycket bra fråga! Vi har hört om detta experimentet under mycket lång tid (c:a 20 år!), men än så länge utan några klara positiva resultat. Så långt kan vi nog vara säkra för om gravitationsvågor skulle påvisas skulle det säkert ge ett nobelpris.
Indirekt har man redan påvisat graviationsvågor eftersom man har kunnat observera att energi försvinner från ett system av två neutronstjärnor, se fråga 473 nedan.
Att direkt observera gravitationsvågor är alltså den primära avsikten, men än så länge har man bara övre gränser, dvs gravitationsvågorna är mindre än detektionsgränsen för apparaten.
LIGO-systemen (man måste ha flera på olika platser för att kunna eliminera lokala störningar) består av två massklumpar i ytterkanterna på ett L där skänklarna är 4 km långa. Med hjälp av laserstrålar och interferens mäter man positionen av massklumparna med en precision på 10-18 m, dvs en tusendel av protonens storlek. Experimenten och uppställningen beskrivs bra och ganska detaljerat iLIGO och nedanstående videor:
Man har alltså genomfört några element, bland annat har man sökt efter gravitationsvågor från en ung pulsar - krabbnebulosa-pulsaren. Ett pressmeddelande (länk 1) säger följande:
LIGO-projektet är alltså ett mycket omfattande och långsiktigt projekt. När man väl detekterat gravitionsvågor kommer man att fortsätta att använda LIGO som ett nytt och unikt verktyg för astronomiska studier, t.ex. av svarta hål och kanske även big bang.
/Peter E 2010-01-20
Linda! Mycket bra fråga! Vi har hört om detta experimentet under mycket lång tid (c:a 20 år!), men än så länge utan några klara positiva resultat. Så långt kan vi nog vara säkra för om gravitationsvågor skulle påvisas skulle det säkert ge ett nobelpris.
Indirekt har man redan påvisat graviationsvågor eftersom man har kunnat observera att energi försvinner från ett system av två neutronstjärnor, se fråga 473 nedan.
Att direkt observera gravitationsvågor är alltså den primära avsikten, men än så länge har man bara övre gränser, dvs gravitationsvågorna är mindre än detektionsgränsen för apparaten.
LIGO-systemen (man måste ha flera på olika platser för att kunna eliminera lokala störningar) består av två massklumpar i ytterkanterna på ett L där skänklarna är 4 km långa. Med hjälp av laserstrålar och interferens mäter man positionen av massklumparna med en precision på 10-18 m, dvs en tusendel av protonens storlek. Experimenten och uppställningen beskrivs bra och ganska detaljerat i
Man har alltså genomfört några element, bland annat har man sökt efter gravitationsvågor från en ung pulsar - krabbnebulosa-pulsaren. Ett pressmeddelande (länk 1) säger följande:
LIGO has evolved over many years to its present capability to produce scientific results of real significance," says Jay Marx of the California Institute of Technology, LIGO's executive director. "The limit on the Crab Pulsar's emission of gravitational waves is but one of a number of important results obtained from LIGO's recent two-year observing period. These results only serve to further our anticipation for the spectacular science that will come from LIGO in the coming years.
LIGO-projektet är alltså ett mycket omfattande och långsiktigt projekt. När man väl detekterat gravitionsvågor kommer man att fortsätta att använda LIGO som ett nytt och unikt verktyg för astronomiska studier, t.ex. av svarta hål och kanske även big bang.
/Peter E 2010-01-20
Vad händer när man "curlar" i curling?
Fråga:
Hej! Skulle vilja veta vad som händer när man "curlar" i curling? Vad är det som gör att stenen glider bättre då?
/Hannes H, Alströmergymnasiet, Alingsås 2010-02-28
Hej! Skulle vilja veta vad som händer när man "curlar" i curling? Vad är det som gör att stenen glider bättre då?
/Hannes H, Alströmergymnasiet, Alingsås 2010-02-28
Svar:
Hannes! Intressant och aktuell fråga med tanke på lag Anette Norbergs insats i OS i Vancouver. Detaljerna för varför stenen "curlar" (avlänkas åt höger eller vänster i förhållande till den ursprungliga riktningen) är komplicerade och även kontroversiella. Vi behandlar detta i avsnittet mot slutet av svaret. Först en video om curling:
Vissa saker är man emellertid helt överens om:
1 Sopandet framför stenen skapar genom friktion värme som smälter isen och ger ett tunnt lager vatten. Detta minskar friktionen mellan stenen och isen.
2 Minskningen i friktion genom sopning medför dels att stenen går längre sträcka för en viss utgångshastighet och dels att den curlar (svänger) mindre.
3 Stenens curlande orsakas av friktionen mot isen och stenens rotation. Observera att man alltid sätter lite rotation på stenen: moturs om man vill att den curlar åt vänster och medurs om man vill ha en högerböj.
Till skillnad från andra sporter (t.ex. golf, bowling, skytte) kan man alltså påverka projektilens rörelse efter det att man släppt iväg den. Svårigheten är att man alltså får två effekter när man sopar: längre bana och mindre curl, och man måste besluta om en optimal kompromiss mellan effekterna.
SVTs kommentatorer vid OS-sändningarna från Vancouver spekulerade om vad resultatet skulle bli om det svenska damlaget skulle spela mot det svenska herrlaget. Man kom fram till att herrarna antagligen skulle vinna, men förklarade inte varför. Jag tror också herrarna skulle vinna helt enkelt för att de är tyngre och starkare, och kan på så sätt kontrollera stenen mer. Om man tittar på statistik för absoluta topp-curlare så har män c:a 90% och kvinnor c:a 80% lyckade stenar (slag).
Detaljerad förklaring till att stenen curlar
Låt oss börja med att göra ett enkelt experiment som du kan göra hemma. Ta ett köksglas (inte mormors finaste glas!) och leta upp ett jämnt, plant underlag, t.ex. en köksbänk. Vänd glaset upp-och-ner och skjut det längs bänken samtidigt som du sätter rotation på glaset, se vänstra bilden i nedanstående figur från Curling Science . Om du som i figuren roterar glaset medurs, så kommer glaset att avlänkas till vänster. Detta resultat är mycket förvånande för en curlare eftersom en curlingsten skulle avlänkas åt motsatt håll, se den högra bilden.
. Om du som i figuren roterar glaset medurs, så kommer glaset att avlänkas till vänster. Detta resultat är mycket förvånande för en curlare eftersom en curlingsten skulle avlänkas åt motsatt håll, se den högra bilden.
Varför reagerar glaset och curlingstenen olika på rotationen? Låt oss börja med att förklara varför glaset rör sig åt vänster. När glaset glider över bänken bromsas det up av en friktionskraft riktad rakt bakåt. Eftersom glasets tyngdpunkt ligger över bänkens plan, så kommer det att utsättas för ett vridmoment riktat bakåt. Trycket på framkanten av glaset blir då högre än trycket på bakkanten. Detta är samma effekt som att en bromsande bil får nosen nertryckt och en accelererande bil får nosen lyft. Eftersom glaset roterar får vi även en friktionskraft riktad åt vänster (friktionskraften är alltid motriktad rörelsen) i glasets framkant och en friktionskraft riktad åt höger i glasets bakkant. Eftersom normalkraften Fn enligt ovan är större i framkanten än i bakkanten blir friktionen större (se nedanstående formel), och vi kommer att få en nettokraft riktad åt vänster.
Varför uppför sig curlingsten annorlunda än glaset? För det första bör man veta att bottenytan på en curlingsten inte är plan, utan den har en skålformad fördjupning i mitten. Anläggningsytan mot isen är alltså en smal ring precis som för det upp-och-nervända glaset.
Skillnaden är att is smälter om den utsätts för högt tryck, se fasdiagrammet i fråga [12715]. Detta är skälet till att en kälke eller skridskor glider så bra på is - friktionen minskas genom ett tunnt vattenskikt. Precis som glaset utsätts stenen för en större normalkraft i framändan än i bakändan. I fallet curlingsten orsakar det högre trycket i framändan att friktionskoefficienten m minskar. Friktionskraften är ju
F = mFn (1)
Eftersom minskningen i friktionskoefficienten är större än ökningen i normalkraften kommer friktionskraften att bli mindre i framändan. Stenen kommer då att i stället böjas av åt höger.
Eftersom förklaringen bygger på att en del is smälts, så bör det ha betydelse vilken temperatur isen har. Om isens temperatur är mycket låg borde man vänta sig att den har svårare att smälta och att friktionen skulle bli större. I länk 1 sägs det om Scotts (Robert_Falcon_Scott ) sydpolsexpedition:
I What Puts the Curl in a Curling Stone? finns ovanstående förklaring till curlande och referenser till fyra vetenskapliga artiklar från Canadian Journal of Physics om olika aspekter på curling. The motion of curling rocks: Experimental investigation and semi-phenomenological description
finns ovanstående förklaring till curlande och referenser till fyra vetenskapliga artiklar från Canadian Journal of Physics om olika aspekter på curling. The motion of curling rocks: Experimental investigation and semi-phenomenological description är en senare artikel av samma författare. I den visas tydligt (men ganska svårgenomträngligt) att ovanstående modell är i stort sett korrekt även om vissa detaljer är oklara. Speciellt gäller detta hur stenen växelverkar med underlaget: växelverkar den med en fix isskiva eller med det rörliga vattnet under stenen? En annan effekt som är svår att förklara är att storleken av curl är i stort sett oberoende av stenens rotationshastighet. Intuitivt väntar man sig att en sten som roterar snabbare curlar mer.
är en senare artikel av samma författare. I den visas tydligt (men ganska svårgenomträngligt) att ovanstående modell är i stort sett korrekt även om vissa detaljer är oklara. Speciellt gäller detta hur stenen växelverkar med underlaget: växelverkar den med en fix isskiva eller med det rörliga vattnet under stenen? En annan effekt som är svår att förklara är att storleken av curl är i stort sett oberoende av stenens rotationshastighet. Intuitivt väntar man sig att en sten som roterar snabbare curlar mer.
I artikeln Comment on the motion of a curling rock framförs en annan modell där inte "våt friktion" (minskande friktionskoefficient) utan "torr friktion" (formel 1 ovan med konstant friktionskoefficient) används. Artikeln är emellertid inte av god kvalité, och slutsatserna är dubiösa.
framförs en annan modell där inte "våt friktion" (minskande friktionskoefficient) utan "torr friktion" (formel 1 ovan med konstant friktionskoefficient) används. Artikeln är emellertid inte av god kvalité, och slutsatserna är dubiösa.
Tester av modellerna
Det vore intressant att testa hur glaset uppför sig på is. Är det någon som har tillgång till mycket jämn is skulle jag vara tacksam om ni ville kummunicera era observationer till mig.
Ett annat experiment som är svårare att åstadkomma är att be ismakarna skruva upp kylningen till max. Skulle det gå att få ner temperaturen så mycket att man inte får någon smältning? Om det går skulle man få några mycket förvånade curlare: stenarna skulle bli mycket korta och curla åt fel håll :-)!
Sopforskning
Sopandet är uppenbarligen en mycket viktig del av curling eftersom detta är lagets möjlighet att påverka stenens bana sedan den släppts. Curling, Olympic training and ice friction fundamentals är ett anslag till några forskare för att förbättra chanserna för det brittiska damlandslaget att försvara sitt guld från 2002 i Turin 2006. Tydligen räckte inte pengarna, för som känt så vann ju lag Norberg!
är ett anslag till några forskare för att förbättra chanserna för det brittiska damlandslaget att försvara sitt guld från 2002 i Turin 2006. Tydligen räckte inte pengarna, för som känt så vann ju lag Norberg!
Vidare studier
Det finns som synes mycket i curling som är av fysikaliskt intresse, och då har vi inte tagit upp kollisioner mellan stenar och bevarandet av rörelsemängd och rörelseenergi.
För mer om curling se Wikipedia-artiklarna på engelska (Curling ) och på svenska (Curling ). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games
). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games . Länk 2 ger en alternativ förklaring.
. Länk 2 ger en alternativ förklaring.
Hannes! Intressant och aktuell fråga med tanke på lag Anette Norbergs insats i OS i Vancouver. Detaljerna för varför stenen "curlar" (avlänkas åt höger eller vänster i förhållande till den ursprungliga riktningen) är komplicerade och även kontroversiella. Vi behandlar detta i avsnittet mot slutet av svaret. Först en video om curling:
Vissa saker är man emellertid helt överens om:
1 Sopandet framför stenen skapar genom friktion värme som smälter isen och ger ett tunnt lager vatten. Detta minskar friktionen mellan stenen och isen.
2 Minskningen i friktion genom sopning medför dels att stenen går längre sträcka för en viss utgångshastighet och dels att den curlar (svänger) mindre.
3 Stenens curlande orsakas av friktionen mot isen och stenens rotation. Observera att man alltid sätter lite rotation på stenen: moturs om man vill att den curlar åt vänster och medurs om man vill ha en högerböj.
Till skillnad från andra sporter (t.ex. golf, bowling, skytte) kan man alltså påverka projektilens rörelse efter det att man släppt iväg den. Svårigheten är att man alltså får två effekter när man sopar: längre bana och mindre curl, och man måste besluta om en optimal kompromiss mellan effekterna.
SVTs kommentatorer vid OS-sändningarna från Vancouver spekulerade om vad resultatet skulle bli om det svenska damlaget skulle spela mot det svenska herrlaget. Man kom fram till att herrarna antagligen skulle vinna, men förklarade inte varför. Jag tror också herrarna skulle vinna helt enkelt för att de är tyngre och starkare, och kan på så sätt kontrollera stenen mer. Om man tittar på statistik för absoluta topp-curlare så har män c:a 90% och kvinnor c:a 80% lyckade stenar (slag).
Detaljerad förklaring till att stenen curlar
Låt oss börja med att göra ett enkelt experiment som du kan göra hemma. Ta ett köksglas (inte mormors finaste glas!) och leta upp ett jämnt, plant underlag, t.ex. en köksbänk. Vänd glaset upp-och-ner och skjut det längs bänken samtidigt som du sätter rotation på glaset, se vänstra bilden i nedanstående figur från Curling Science
Varför reagerar glaset och curlingstenen olika på rotationen? Låt oss börja med att förklara varför glaset rör sig åt vänster. När glaset glider över bänken bromsas det up av en friktionskraft riktad rakt bakåt. Eftersom glasets tyngdpunkt ligger över bänkens plan, så kommer det att utsättas för ett vridmoment riktat bakåt. Trycket på framkanten av glaset blir då högre än trycket på bakkanten. Detta är samma effekt som att en bromsande bil får nosen nertryckt och en accelererande bil får nosen lyft. Eftersom glaset roterar får vi även en friktionskraft riktad åt vänster (friktionskraften är alltid motriktad rörelsen) i glasets framkant och en friktionskraft riktad åt höger i glasets bakkant. Eftersom normalkraften Fn enligt ovan är större i framkanten än i bakkanten blir friktionen större (se nedanstående formel), och vi kommer att få en nettokraft riktad åt vänster.
Varför uppför sig curlingsten annorlunda än glaset? För det första bör man veta att bottenytan på en curlingsten inte är plan, utan den har en skålformad fördjupning i mitten. Anläggningsytan mot isen är alltså en smal ring precis som för det upp-och-nervända glaset.
Skillnaden är att is smälter om den utsätts för högt tryck, se fasdiagrammet i fråga [12715]. Detta är skälet till att en kälke eller skridskor glider så bra på is - friktionen minskas genom ett tunnt vattenskikt. Precis som glaset utsätts stenen för en större normalkraft i framändan än i bakändan. I fallet curlingsten orsakar det högre trycket i framändan att friktionskoefficienten m minskar. Friktionskraften är ju
F = mFn (1)
Eftersom minskningen i friktionskoefficienten är större än ökningen i normalkraften kommer friktionskraften att bli mindre i framändan. Stenen kommer då att i stället böjas av åt höger.
Eftersom förklaringen bygger på att en del is smälts, så bör det ha betydelse vilken temperatur isen har. Om isens temperatur är mycket låg borde man vänta sig att den har svårare att smälta och att friktionen skulle bli större. I länk 1 sägs det om Scotts (
Another key factor when considering the slipperiness of ice is temperature. Captain Scott noted during his Antarctic travels that once the temperature fell below -35 degrees C it become incredibly hard to pull sleds through the snow. This was because the heat produced by the friction between sled and snow was not enough to warm the ice to its melting point (0 degrees C) so no lubricating melt water was produced. Scott and his companions may as well have been pulling their sleds through sand. The closer the temperature of the ice is to its melting point the more melt lubricant is produced by sliding and the more slippery ice becomes.
I What Puts the Curl in a Curling Stone?
I artikeln Comment on the motion of a curling rock
Tester av modellerna
Det vore intressant att testa hur glaset uppför sig på is. Är det någon som har tillgång till mycket jämn is skulle jag vara tacksam om ni ville kummunicera era observationer till mig.
Ett annat experiment som är svårare att åstadkomma är att be ismakarna skruva upp kylningen till max. Skulle det gå att få ner temperaturen så mycket att man inte får någon smältning? Om det går skulle man få några mycket förvånade curlare: stenarna skulle bli mycket korta och curla åt fel håll :-)!
Sopforskning
Sopandet är uppenbarligen en mycket viktig del av curling eftersom detta är lagets möjlighet att påverka stenens bana sedan den släppts. Curling, Olympic training and ice friction fundamentals
Vidare studier
Det finns som synes mycket i curling som är av fysikaliskt intresse, och då har vi inte tagit upp kollisioner mellan stenar och bevarandet av rörelsemängd och rörelseenergi.
För mer om curling se Wikipedia-artiklarna på engelska (
 ). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games
). Fler videos om olympiska vintersporter finns här: Science of the Olympic Winter Games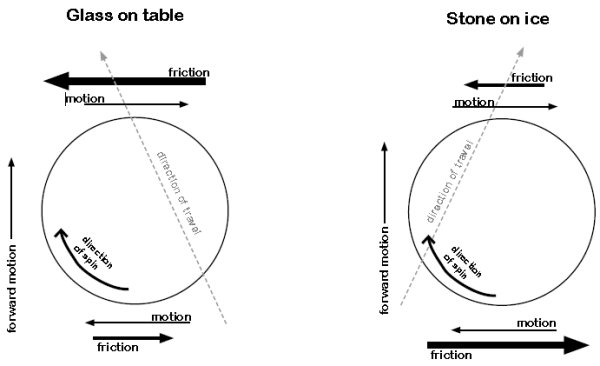
Rymdsegel
Fråga:
Är det möjligt att få upp ett föremål högre hastigheter än ljusets? Om man sänder ut en sond i rymden med ett solsegel som endast påverkas av den kraft som ger den en accellererad rörelse, dvs. Den kraft som solseglet ger den. Då borde den väll kunna ta sig upp i högre hastigheter än ljuset efter ett tag. Eller slutar vissa fysiska lagar gälla vid dessa hastigheter?
/David E, NTM, Danderyd 2010-04-01
Är det möjligt att få upp ett föremål högre hastigheter än ljusets? Om man sänder ut en sond i rymden med ett solsegel som endast påverkas av den kraft som ger den en accellererad rörelse, dvs. Den kraft som solseglet ger den. Då borde den väll kunna ta sig upp i högre hastigheter än ljuset efter ett tag. Eller slutar vissa fysiska lagar gälla vid dessa hastigheter?
/David E, NTM, Danderyd 2010-04-01
Svar:
Nej, det fungerar inte av flera skäl. Först teoretiskt: den kostar oändligt mycket energi att accelerera ett materiellt föremål till ljushastigheten. Föremålet blir nämligen oändligt tungt (relativistisk massa). Om föremålet fick upp farten skulle solstrålningen bli mindre och mindre effektiv dels för att den blir svagare (föremålet är längre bort) och för att det skulle bli rödförskjutet och därmed ge en mindre "puff".
Solsegel fungerar emellertid i princip, men eftersom de är ganska ineffektiva (se nedan) har de inte prioriterats av NASA. Se länk 1 för historik. Man gjorde ett försök för ett tag sedan med en satellit som hette NanoSail-D, men uppskjutningen misslyckades (länk 2).
Fördelen med solsegel är att man kan accelerera utan bränsle. Nackdelar är att de kan bara användas i det inre solsystemet (där solstrålningen är hög) och att man är bunden till att accelerera i stort sett i riktning från solen, dvs styrförmågan är mycket begränsad. Dessutom är det svårt att tillverka tillräckligt stadiga segel. Seglet väger en hel del eftersom det måste vara ganska stort.
Hur effektivt är ett solsegel?
Rörelsemängden för elektromagnetisk strålning ges av
p = E/c
där E är strålningens energi och c är ljushastigheten. Kraften som påverkar ett segel med ytan A ges av
F = dp/dt = (dE/dt)A/c
Effekten per ytenhet dE/dt är den s.k.solarkonstanten 1370 W/m2 (instrålningen av solljus på jordens avstånd).
Vi kompletterar ovanstående uttryck med dels en faktor 2 eftersom ljuset speglas i seglet och alltså överlämnar rörelsemängden 2p. Vi inför även en verkningsgrad h för att ta hänsyn till om seglet inte är vinkerätt mot solstrålningen eller om seglet är krökt:
F = 2h(dE/dt)A/c
Accelerationen blir, om farkostens massa (inklusive seglet) är m och verkningsgraden 1:
a = F/m = 2(dE/dt)c-1(A/m) = 21370(3108)-1(A/m) =
= 9.110-6(A/m) [Js-1m-2sm-1m2kg-1] = 9.110-6(A/m) [m/s2]
Med massan m=1000 kg och segelytan A=10000 m2 (100mX100m) får vi accelerationen
a = 9.110-6(10000/1000) = 9.110-5 (m/s)/s = 6060249.110-5 (m/s)/dygn = 7.9 (m/s)/dygn
Med tanke på att hastigheter i solsystemet är av storleksordningen tiotals km/s så är detta en mycket liten acceleration. Det skulle t.ex. fordras 127 dagar för att ändra hastigheten med 1 km/s!
Nedan är en bild på NanoSail-D, seNanoSail-D .
Nej, det fungerar inte av flera skäl. Först teoretiskt: den kostar oändligt mycket energi att accelerera ett materiellt föremål till ljushastigheten. Föremålet blir nämligen oändligt tungt (relativistisk massa). Om föremålet fick upp farten skulle solstrålningen bli mindre och mindre effektiv dels för att den blir svagare (föremålet är längre bort) och för att det skulle bli rödförskjutet och därmed ge en mindre "puff".
Solsegel fungerar emellertid i princip, men eftersom de är ganska ineffektiva (se nedan) har de inte prioriterats av NASA. Se länk 1 för historik. Man gjorde ett försök för ett tag sedan med en satellit som hette NanoSail-D, men uppskjutningen misslyckades (länk 2).
Fördelen med solsegel är att man kan accelerera utan bränsle. Nackdelar är att de kan bara användas i det inre solsystemet (där solstrålningen är hög) och att man är bunden till att accelerera i stort sett i riktning från solen, dvs styrförmågan är mycket begränsad. Dessutom är det svårt att tillverka tillräckligt stadiga segel. Seglet väger en hel del eftersom det måste vara ganska stort.
Hur effektivt är ett solsegel?
Rörelsemängden för elektromagnetisk strålning ges av
p = E/c
där E är strålningens energi och c är ljushastigheten. Kraften som påverkar ett segel med ytan A ges av
F = dp/dt = (dE/dt)A/c
Effekten per ytenhet dE/dt är den s.k.
Vi kompletterar ovanstående uttryck med dels en faktor 2 eftersom ljuset speglas i seglet och alltså överlämnar rörelsemängden 2p. Vi inför även en verkningsgrad h för att ta hänsyn till om seglet inte är vinkerätt mot solstrålningen eller om seglet är krökt:
F = 2h(dE/dt)A/c
Accelerationen blir, om farkostens massa (inklusive seglet) är m och verkningsgraden 1:
a = F/m = 2(dE/dt)c-1(A/m) = 21370(3108)-1(A/m) =
= 9.110-6(A/m) [Js-1m-2sm-1m2kg-1] = 9.110-6(A/m) [m/s2]
Med massan m=1000 kg och segelytan A=10000 m2 (100mX100m) får vi accelerationen
a = 9.110-6(10000/1000) = 9.110-5 (m/s)/s = 6060249.110-5 (m/s)/dygn = 7.9 (m/s)/dygn
Med tanke på att hastigheter i solsystemet är av storleksordningen tiotals km/s så är detta en mycket liten acceleration. Det skulle t.ex. fordras 127 dagar för att ändra hastigheten med 1 km/s!
Nedan är en bild på NanoSail-D, se

Vid backhoppning borde inte massan spela någon roll för hastigheten vid själva uthoppet (väl?).
Fråga:
Vid backhoppning borde inte massan spela någon roll för hastigheten vid själva uthoppet (väl?). Varför är det då en "trend" för backhoppare att de ska var så små som möjligt? Är det för att minska luftmotståndet?
/Sara L, Fredrikabremer gymnasiet, Haninge 2010-04-07
Vid backhoppning borde inte massan spela någon roll för hastigheten vid själva uthoppet (väl?). Varför är det då en "trend" för backhoppare att de ska var så små som möjligt? Är det för att minska luftmotståndet?
/Sara L, Fredrikabremer gymnasiet, Haninge 2010-04-07
Svar:
Sara! Intressant fråga, speciellt med tanke på tidigare svar om störtlopp! Jo, massan har betydelse för uthoppshastigheten. Se fråga [869] där det visas att hastigheten för en tyngre störtloppsåkare är större än för en mindre.
Hur kan det då komma sig att de bästa backhopparna ofta är små och lätta? En antydan får man om man jämför dräkterna. En störtloppsåkare har en tätsittande dräkt för att minimera luftmotståndet, medan en backhoppare har breda skidor och en dräkt som är "fem nummer för stor". Det är alltså inte farten i backen som bestämmer hopplängden utan förmågan att sväva långt i luften. För detta behöver man liten vikt och stor yta. Den stora ytan åstadkommer man dels med en väl tilltagen dräkt och dels med den s.k. V-stilen (Jan Boklöv,V-style ) som ger mer lyftkraft på kroppen eftersom den inte skuggas av skidorna - större "vinge" ger större lyftkraft. Hopplängden bestäms alltså till en stor del av aerodynamiken i luften.
En annan aspekt som gör farten i backen mindre utslagsgivande är att en stor del av uthoppshastigheten kommer från ett väl tajmat uthopp. Det är här och i förmågan att hålla kropp och skidor i en effektiv vinkel som skiljer bra hoppare från mindre bra.
Se vidare Backhoppning och
och Ski_jumping . Bilden nedan är från Wikimedia Commons.
/fa2010_4
Sara! Intressant fråga, speciellt med tanke på tidigare svar om störtlopp! Jo, massan har betydelse för uthoppshastigheten. Se fråga [869] där det visas att hastigheten för en tyngre störtloppsåkare är större än för en mindre.
Hur kan det då komma sig att de bästa backhopparna ofta är små och lätta? En antydan får man om man jämför dräkterna. En störtloppsåkare har en tätsittande dräkt för att minimera luftmotståndet, medan en backhoppare har breda skidor och en dräkt som är "fem nummer för stor". Det är alltså inte farten i backen som bestämmer hopplängden utan förmågan att sväva långt i luften. För detta behöver man liten vikt och stor yta. Den stora ytan åstadkommer man dels med en väl tilltagen dräkt och dels med den s.k. V-stilen (Jan Boklöv,
En annan aspekt som gör farten i backen mindre utslagsgivande är att en stor del av uthoppshastigheten kommer från ett väl tajmat uthopp. Det är här och i förmågan att hålla kropp och skidor i en effektiv vinkel som skiljer bra hoppare från mindre bra.
Se vidare Backhoppning
 och
och /fa2010_4

Vem kom på att två föremål oavsett vikten faller till marken samtidigt?
Fråga:
vem som kom på att två föremål oavsett vikten faller på marken samtidigt?
/Frank M, Nacka, stockholm 2010-09-04
vem som kom på att två föremål oavsett vikten faller på marken samtidigt?
/Frank M, Nacka, stockholm 2010-09-04
Svar:
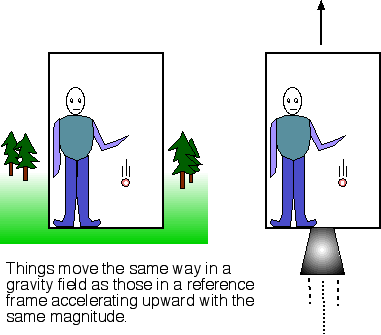
Frank! Det var Galileo Galilei som först utförde experiment och resonerade om detta, seGalileo_GalileiPhysics . Einstein använde ekvivalensen mellan acceleration och gravitation som ett grundantagande för sin allmänna relativitetsteori. Av detta följer direkt att alla kroppar faller lika snabbt i ett tyngdkraftfält. Man kan alltså byta ut ett tyngdkraftfält med en acceleration i motsatt riktning.
Låt oss säga du står i en hiss som befinner sig på marken (se nedanstående bild från länk 1). Du släpper ett föremål som faler nedåt. På grund av ovanstående ekvivalensprincip kan vi byta ut tyngdkraftfältet mot en lika stor acceleration uppåt. Det är uppenbart i detta fall (till höger i figuren) att fallhastigheten är helt oberoende av massan hos föremålet eftersom det ju står stilla (påverkas inte av någon kraft) medan hissen och du (som står på golvet) accelererar uppåt.
Se fråga [13663] för en kul demonstration.
Tillägg om ekvivalensprincipen
Engelska Wikipedia definierarekvivalensprincipen som (Equivalence_principle ):
Ekvivalensprincipen förekommer även i en svagare form i klassisk newtonsk fysik: ekvivalensen mellan tung och trög massa, dvs att massan m som förekommer i uttrycket
är samma som förekommer i Newtons gravitationslag
dvs accelerationen a ges av
oberoende av m.
Frank! Det var Galileo Galilei som först utförde experiment och resonerade om detta, se
Låt oss säga du står i en hiss som befinner sig på marken (se nedanstående bild från länk 1). Du släpper ett föremål som faler nedåt. På grund av ovanstående ekvivalensprincip kan vi byta ut tyngdkraftfältet mot en lika stor acceleration uppåt. Det är uppenbart i detta fall (till höger i figuren) att fallhastigheten är helt oberoende av massan hos föremålet eftersom det ju står stilla (påverkas inte av någon kraft) medan hissen och du (som står på golvet) accelererar uppåt.
Se fråga [13663] för en kul demonstration.
Tillägg om ekvivalensprincipen
Engelska Wikipedia definierar
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's observation that the gravitational "force" as experienced locally while standing on a massive body (such as the Earth) is actually the same as the pseudo-force experienced by an observer in a non-inertial (accelerated) frame of reference.
Ekvivalensprincipen förekommer även i en svagare form i klassisk newtonsk fysik: ekvivalensen mellan tung och trög massa, dvs att massan m som förekommer i uttrycket
F = m a
är samma som förekommer i Newtons gravitationslag
F = G M m/r2
dvs accelerationen a ges av
a = G M/r2
oberoende av m.
Av detta följer att alla föremål faller med samma acceleration i ett gravitationsfält (bortsett från luftmotståndet).
Länk 2 innehåller Galileis teoretiska argumentation för ekvivalensprincipen. Se A Cultural History of Gravity and the Equivalence Principle![]() för diskussion om tidigare funderingar (den Bysantinske filosofen Iohannes Philiponus).
för diskussion om tidigare funderingar (den Bysantinske filosofen Iohannes Philiponus).
Hur kommer det sig att ett spaghettistrå aldrig kan brytas i färre än tre delar?
Fråga:
Hejsan!
Hur kommer det sig att ett spaghettistrå aldrig kan brytas i färre än tre delar? Finns det någon enkel förklaring?
Jag har själv testat och påståendet stämmer, förutsatt att man håller i ändarna av strået när man spänner det.
Tack på förhand
/Oscar
/Oscar M, Korrespondensgymnasiet, Torsås 2010-09-15
Hejsan!
Hur kommer det sig att ett spaghettistrå aldrig kan brytas i färre än tre delar? Finns det någon enkel förklaring?
Jag har själv testat och påståendet stämmer, förutsatt att man håller i ändarna av strået när man spänner det.
Tack på förhand
/Oscar
/Oscar M, Korrespondensgymnasiet, Torsås 2010-09-15
Svar:
Hej Oscar! Nej, det är ett mycket komplicerat problem. Problemet har studerats teoretiskt av ett par franska fysiker, se länk 1. Artikeln är i en av världens mest respekterade fysik-tidsskrifter, Physical Review Letters.
Enkelt uttryckt ger brottet upphov till en våldsam svängning i spagettistrået. Svängningen är så våldsam att strået böjs mer än hållfastheten tillåter. Man får alltså minst ytterligare ett brott. Det är en bra observation att man måste hålla i ändarna av strået. Håller man nära mitten dämpar man svängningen och strået bryts inte.
Det kan tyckas märkligt att man publicerar en artikel om ett såpass trivialt problem. Det är emellertid så att lösningen kan tänkas tillämpas på andra, mer intressanta, hållfasthetsproblem.
/Peter E 2010-09-15
Hej Oscar! Nej, det är ett mycket komplicerat problem. Problemet har studerats teoretiskt av ett par franska fysiker, se länk 1. Artikeln är i en av världens mest respekterade fysik-tidsskrifter, Physical Review Letters.
Enkelt uttryckt ger brottet upphov till en våldsam svängning i spagettistrået. Svängningen är så våldsam att strået böjs mer än hållfastheten tillåter. Man får alltså minst ytterligare ett brott. Det är en bra observation att man måste hålla i ändarna av strået. Håller man nära mitten dämpar man svängningen och strået bryts inte.
Det kan tyckas märkligt att man publicerar en artikel om ett såpass trivialt problem. Det är emellertid så att lösningen kan tänkas tillämpas på andra, mer intressanta, hållfasthetsproblem.
/Peter E 2010-09-15
Hur påverkas vädret av corioliskraften?
Fråga:
Har en fråga om corioliskraften, eller snarare en bra förklaring på dess inverkan. Hur påverkas vädret egentligen? Eller är det en fråga för SMHI??
/jan g, Enskilda Gymnasiet, Stockholm 2010-11-13
Har en fråga om corioliskraften, eller snarare en bra förklaring på dess inverkan. Hur påverkas vädret egentligen? Eller är det en fråga för SMHI??
/jan g, Enskilda Gymnasiet, Stockholm 2010-11-13
Svar:
Jan! Det låter som en meteorologifråga, men corioliskraften orsakar ju rotationen hos lågtryck, högtryck och tropiska cykloner. Den påverkar även havsströmmar, passadvindar, jetströmmar, mm, som ju även de påverkar vädret. Se fråga [3160] för allmänt om corioliskraften.
Bilden nedan från Wikimedia Commons visar ett lågtryck över Island. I ett lågtryckssystem har man en luftström utifrån och inåt centrum. På grund av jordens rotation kommer på norra halvklotet en S-N gående luftström avlänkas mot öster och en N-S luftström att avlänkas mot väster, se CorioliseffektenCorioliskrafter_orsakade_av_jordens_rotation
visar ett lågtryck över Island. I ett lågtryckssystem har man en luftström utifrån och inåt centrum. På grund av jordens rotation kommer på norra halvklotet en S-N gående luftström avlänkas mot öster och en N-S luftström att avlänkas mot väster, se CorioliseffektenCorioliskrafter_orsakade_av_jordens_rotation . (Alltid påverkan åt höger på norra halvklotet, åt vänster på södra.) Ett lågtryck på norra halvklotet får alltså en rotation moturs. För storskaliga system är som synes corioliskraften mycket betydelsefull, och man måste ta hänsyn till den för väderprognoser. Se vidare SMHIs webbsajt, t.ex. länk 1 och 2 nedan.
. (Alltid påverkan åt höger på norra halvklotet, åt vänster på södra.) Ett lågtryck på norra halvklotet får alltså en rotation moturs. För storskaliga system är som synes corioliskraften mycket betydelsefull, och man måste ta hänsyn till den för väderprognoser. Se vidare SMHIs webbsajt, t.ex. länk 1 och 2 nedan.
Jan! Det låter som en meteorologifråga, men corioliskraften orsakar ju rotationen hos lågtryck, högtryck och tropiska cykloner. Den påverkar även havsströmmar, passadvindar, jetströmmar, mm, som ju även de påverkar vädret. Se fråga [3160] för allmänt om corioliskraften.
Bilden nedan från Wikimedia Commons
 . (Alltid påverkan åt höger på norra halvklotet, åt vänster på södra.) Ett lågtryck på norra halvklotet får alltså en rotation moturs. För storskaliga system är som synes corioliskraften mycket betydelsefull, och man måste ta hänsyn till den för väderprognoser. Se vidare SMHIs webbsajt, t.ex. länk 1 och 2 nedan.
. (Alltid påverkan åt höger på norra halvklotet, åt vänster på södra.) Ett lågtryck på norra halvklotet får alltså en rotation moturs. För storskaliga system är som synes corioliskraften mycket betydelsefull, och man måste ta hänsyn till den för väderprognoser. Se vidare SMHIs webbsajt, t.ex. länk 1 och 2 nedan.
Arbete på ett löpband
Fråga:
Min fru springer på ett löpband som går att luta. Jag påstår att hon i teknisk mening inte utför mer arbete när det lutar uppåt eftersom henne massa inte flyttas uppåt. Hon påstår att det går tyngre (jag har inte provat). Denna känsla av att det går tyngre har enl. mig möjligen en fysiologisk förklaring som jag inte kan beskriva.
/Bertil S, Hackås 2010-11-20
Min fru springer på ett löpband som går att luta. Jag påstår att hon i teknisk mening inte utför mer arbete när det lutar uppåt eftersom henne massa inte flyttas uppåt. Hon påstår att det går tyngre (jag har inte provat). Denna känsla av att det går tyngre har enl. mig möjligen en fysiologisk förklaring som jag inte kan beskriva.
/Bertil S, Hackås 2010-11-20
Svar:
Tyvärr Bertil, din fru har rätt (igen :-))! Man kan resonera på flera sätt, till exempel: När foten är i kontakt med bandet transporteras den lite neråt. Detta måste kompenseras i nästa steg, så det är en riktig uppförsbacke. Om du tittar noga så flyttar sig tyngdpunkten på löparen upp och ner. Om bandet lutar, så måste denna rörelse vara större för att löparen skall komma rätt i nästa steg. Att springa på ett löpband är helt ekvivalent med normal löpning med undantag för luftmotståndet.
Andra, eventuellt förvånande, fakta är att man kan bli trött utan att utföra arbete (fråga [13327]) och att utfört arbete beror på vilket inertialsystem man befinner sig i (fråga [14380]).
/Peter E 2010-11-20
Tyvärr Bertil, din fru har rätt (igen :-))! Man kan resonera på flera sätt, till exempel: När foten är i kontakt med bandet transporteras den lite neråt. Detta måste kompenseras i nästa steg, så det är en riktig uppförsbacke. Om du tittar noga så flyttar sig tyngdpunkten på löparen upp och ner. Om bandet lutar, så måste denna rörelse vara större för att löparen skall komma rätt i nästa steg. Att springa på ett löpband är helt ekvivalent med normal löpning med undantag för luftmotståndet.
Andra, eventuellt förvånande, fakta är att man kan bli trött utan att utföra arbete (fråga [13327]) och att utfört arbete beror på vilket inertialsystem man befinner sig i (fråga [14380]).
/Peter E 2010-11-20
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.
Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar

