Vill du ha ett snabbt svar - sök i databasen: Anpassad Google-sökning 45 frågor/svar hittade Kraft-Rörelse [21379] Svar: Se fråga 14250 Nyckelord: relativitetsteorin, speciella [45]; relativistiskt massberoende [4]; Kraft-Rörelse [21358] Svar: Här är några andra liknande (ganska avancerade) fall: Fråga 13654 Se fråga 20601 Nyckelord: relativitetsteorin, speciella [45]; relativitetsteorin, allmänna [33]; svart hål [51]; Kraft-Rörelse [21355] Svar: För höga hastigheter måste man använda det relativistiska uttrycket för addition av hastigheter, se fråga 782 Nyckelord: addition av hastigheter [2]; relativitetsteorin, speciella [45]; Kraft-Rörelse [21219]
1. När man bestämmer referensram och längdkontraktion för någonting beräknar man ju fart och riktning relativt någonting annat. Betyder inte det att allting har i stort sett oändligt många referensramar och längdkontraktioner eftersom man kan jämföra fart och riktning med allt annat som har en annan fart och riktning? 2. Jag har förstått att längdkontraktion fungerar för all materia och således också elementarpartiklar. Men en elementarpartikel, som till exempel elektronen, ändrar ju riktning hela tiden. Ändras då också referensram för elektronen vid varje riktningsförändring? Det blir väl en konstant förändring? Svar: 2) Ja, även elementarpartiklar påverkas av längdkontraktionen. Man kan inte observera kontraktionen direkt, men en snabb elektron antar "pannkaksform" och detta påverkar det elektriska fältet. Se Length_contraction#Experimental_verifications Se även bilden nedan från länk 1. Den visar pannkaksformen hos kolliderande tunga joner. Se även fråga 20459 Kolliderande tunga joner antar pannkaksform på grund av längdkontraktionen: Nyckelord: längdkontraktion [6]; relativitetsteorin, speciella [45]; Ljud-Ljus-Vågor [20970] Svar: Se vidare Speed_of_light#Fundamental_role_in_physics Se även fråga 13218 Nyckelord: relativitetsteorin, speciella [45]; ljushastigheten [24]; 1 http://www.desy.de/user/projects/Physics/Relativity/SpeedOfLight/speed_of_light.html Kraft-Rörelse [20847] Jag minns att när vi frågade vår lärare vad hans upptäckter medförde så sa han att om mänskligheten tror att universum utvidgas trots att det inte sker så spelar det absolut ingen roll. All astronomi är hjärnföroreningar! Om vetenskapsmän uppfattar Einstein som en gud så ser de inte de uppenbara fel som finns i hans teorier. Eller också är det så att de inte vill se felen för då förlorar de alla karriärmöjligheter… Jag har försökt att hitta kommentarer till Jan Slowaks forskning utan att lyckas. Det som känns konstigt är att felräkningarna som min lärare påpekade på 60-talet finns beskrivna i Jan Slowaks bok. Kan det vara så att fortfarande ingen forskare vågar se Einsteins felräkningar?
Tyvärr så omkom min geniale lärare i en trafikolycka något år senare.
/Harald Svar: Den speciella relativitetsteorin bygger på två mycket rimliga antaganden, se fråga 16263 Det råder stor enighet i vetenskapssamhället att SR och även AR ger en mycket bra beskrivning av det vi kan observera. De utgör inte den slutgiltiga teorin eftersom integreringen av AR med kvantmekaniken saknas. Det finns flera exempel på författare som kritiserat och gjort om delar av den moderna fysiken. Det mest omfattande exemplet är Randell Mills som skrivit en bok på över 1000 sidor med värdelöst nonsens, se fråga 14237 Sannolikheten att en person i dag skulle hitta grundläggande fel i en etablerad teori som SR är om inte noll så åtminstone mycket nära noll. Einstein själv framställs ibland som en isolerad kuf med revolutionerande idéer. Detta är långt ifrån sanningen. Han hade mycket bra kontroll på den aktuella vetenskapliga utvecklingen de första åren på 1900-talet. SR var en frukt av flera fysikers arbeten, men det var Einstein som "knöt ihop säcken" och skapade en konsistent teori. Nyckelord: relativitetsteorin, speciella [45]; pseudovetenskap [11]; 1 https://www.bokus.com/cgi-bin/product_search.cgi?authors=Jan%20Slowak Kraft-Rörelse [20741] Svar: Däremot kan en skugga eller en laserstråle röra sig snabbare än ljuset utan att det strider mot den speciella relativitetsteorin. Tänk att du riktar en laserstråle mot ett avlägset objekt. Du kan rikta om laserstrålen med en mycket liten rörelse så att ljusfläcken verkar röra sig mycket snabbt, faktiskt snabbare än ljuset. Detta strider inte mot relativitetsteorin eftersom ingen energi (massa) eller information överföres av ljusfläcken. Man har observerat astronomiska objekt (exploderande stjärnor) som uppvisar ovanstående effekt, se nedanstående video. Se även Faster-than-light#Light_spots_and_shadows Nyckelord: relativitetsteorin, speciella [45]; ljushastigheten [24]; Kraft-Rörelse [20460] 2 Hur kommer det säg att en foton har hel spinn medans elektron halvt? Varför får en foton hel spinn? 3 Min lärrare sa att Fotoner har ingen massa men hur kan då Albert Einsteins lag stämma? E=mc² Svar: Laddade partiklar har ett magnetiskt moment som skapas av spinnet som i detta avseende liknar en rotation. Spinn kan anta heltalsvärden (0,1,2..., bosoner) och halvtalsvärden (1/2,3/2,5/2..., fermioner). Endast fermioner lyder pauliprincipen (se fråga 18298 2 Det bara är så. 3 Din lärare har rätt om man med massa menar vilomassa. För fotoner och relativistiska partiklar måste du tillämpa den generella sambandet för relativistisk energi (se Mass–energy_equivalence Er = sqrt{(m0c2)2 + (pc)2} där m0 är vilomassan och p är rörelsemängden. För en foton med vilomassan noll (m0=0) får vi E=pc. För en stillastående partikel (p=0) får vi E=m0c2. Se även fråga 12753 Nyckelord: kvantmekanik [30]; relativitetsteorin, speciella [45]; Kraft-Rörelse [20002] Jag har lite problem med att härleda formlerna för längdkontraktion och tidsdilation från Lorentztransformationen och undrar var jag tänker fel. Jag börjar med att introducera två godtyckliga händelser i rumtiden, (t₁, x₁, y₁, z₁) och (t₂,x₂, y₂, z₂). Vidare, för att förenkla problemet, låter jag y₁, = z₁ = y₂ = z₂ = 0. Om jag definierar metriken d_x(x2', x1') = x2'- x1' finner jag att d_x = gamma*(x2 - v*t2) - gamma*(x1 - v*t1). Om jag nu resonerar att t2 = t1 eftersom jag mäter båda händelserna vid samma tidpunkt kan jag ersätta t2 med t1 och få d_x(x2', x1') = Δx' = gamma * Δx, vilket stämmer. Men om detta görs för metriken d_t(t2', t1') = t2'- t1' och villkoret x1 = x2 får jag istället d_t(t2', t1') = Δt' = gamma * Δt, när Δt' egentligen ska vara Δt/gamma. Varför kan jag inte anta x2 = x1, och hur härleder jag formeln för tidsdilation från Lorentztransformationen annars? Svar: I artikeln Tidsdilatation Se även Längdkontraktion eller lyssna på föreläsningen Nyckelord: relativitetsteorin, speciella [45]; tidsdilatation [6]; längdkontraktion [6]; Kraft-Rörelse [19913] Svar: I länk 1 diskuteras om överlappsgränsen mellan skänklarna hos en lång sax kan röra sig fortare än ljuset. Eftersom gränsen inte är ett materiellt föremål kan det röra sig snabbare än ljuset. Nyckelord: ljushastigheten [24]; relativitetsteorin, speciella [45]; Ljud-Ljus-Vågor [19723] Ursprunglig fråga: Jag läser just nu om elektromagnetiska svängningskretsar och hur radiovågor alstras, men det finns något jag inte riktigt förstår. Om man utgår från förklaringen med svängningskretsen där energi växlar mellan att vara elektrisk mellan kondensationsplattorna och magnetisk i spolen, kommer man fram till att det magnetiska fältet är minimalt när det elektriska fältet är maximalt och vice versa. Men när vi talar om elektromagnetiska vågor är inte fälten förskjutna relativt varandra med pi/2 rad, de är ju i fas!Jag har försökt googla runt och stötte på begreppen induktionsfält och strålningsfält, men ingen riktig ingående förklaring på vad dessa är och hur de gör att fälten hamnar i fas, så jag hade varit tacksam om jag hade fått en här! Mvh, Rose Svar: Classically, EMR consists of electromagnetic waves, which are synchronized oscillations of electric and magnetic fields that propagate at the speed of light. The oscillations of the two fields are perpendicular to each other and perpendicular to the direction of energy and wave propagation, forming a transverse wave. Electromagnetic waves can be characterized by either the frequency or wavelength of their oscillations to form the electromagnetic spectrum. (Electromagnetic_radiation Maxwells ekvationer ger en vågekvation där amplituden på stort avstånd från källan (se nedanstående figur) avtar som 1/r. Detta är ditt strålningsfält. Fälten ser ut som i figuren i fråga 15035 Nära källan är fälten mycket mer komplicerade eftersom vi har både laddningar och magnetism. Dessa (induktionsfältet) avtar emellertid hastigare än 1/r och försvinner på stort avstånd. Det är alltså bara strålningsfältet, som avtar som 1/r, som överlever på stort avstånd. Det är alltså amplituden på fälten som avtar som 1/r. Energitransporten ges emellertid av Poyntings vektor (Poynting_vector#Plane_waves P = konst*ExB = konst*E2/c, och avtar, som sig bör, som 1/r2. Se även Electromagnetic_radiation#Near_and_far_fields Hoppas det blev lite klarare, Rose, men detta är inte helt lätt. Bra föreläsningar om Maxwells ekvationer och elektromagnetisk strålning av professor Shankar (Yale) finns under länk 1 och 2. Mot slutet av föreläsning 2 visar föreläsaren hur den magnetiska kraften uppkommer som en relativistisk effekt på laddningar som rör sig. Det var detta som fick Einstein att utveckla sin speciella relativitetsteori. Nyckelord: elektromagnetisk strålning [21]; Maxwells ekvationer [3]; relativitetsteorin, speciella [45]; 1 https://www.youtube.com/watch?v=yINtzw63Knc Kraft-Rörelse [19549] Jag har lite svårt att greppa vissa appliceringar av massa-energi ekvivalens och tänkte att jag kanske kan få hjälp här att reda ut vad det är jag har fått om bakfoten. Flera uppgifter jag stött på på området är av typen "Ett föremål med massan 2 kg färdas med hastigheten 30 m/s. Hur mycket ökar massan?",eller "Ett batteri laddas upp med energin 5 kJ, hur mycket ökar massan?". Grundat på tidigare fysikkunskaper anser jag att rörelseenergin ökar i det första exemplet och den elektriska potentiella energin i det andra, men enligt min bok ger dessa energiändringar även ökad massa enligt E = mc^2. För mina öron låter det här som en dubbel energiökning, dvs. en ökning av kinetisk/potentiell energi OCH en lika stor ökning i massa, men det låter ju som ett brott mot energiprincipen! Så frågan är helt enkelt: Vart tänker jag fel? Tack så mycket! Mycket Vänliga Hälsningar, Aletta Svar: Första formeln i Mass–energy_equivalence#Mass–velocity_relationship E = m0c2 + m0v2/2 Lägg märke till att här har vi det klassiska uttrycket för kinetiska energin. För "normala" exempel är massökningen mycket liten. Man räknar enkelt ut den med formeln DE [J] =
Dm*c2 [kg*(m/s)2=N*m=J] 2 kg med hastigheten 30 m/s ger kinetiska energin 2*900/2 = 900 J vilket motsvarar Dm = 900/(3*108)2 = 100/1016 = 10-14 kg = 0.00000000000001 kg. 5000 J motsvarar massan Dm = 5000/(3*108)2 = 5.7*10-14 kg Som sagt, det är ingen dubbelräkning. Det är helt enkelt så att den ökade elektriska energin väger lite grann. Nyckelord: relativistiskt massberoende [4]; relativitetsteorin, speciella [45]; Kraft-Rörelse [19497] Svar: ds2 = c2dt2 - dx12 - dx22. Vi ser att avståndet beror både på rumskoordinaterna och på tiden. Sammankopplingen av rum och tid illustreras ofta av arr rymd/tids-diagram, se nedan. (För att kunna rita det har vi tagit bort en rumsdimension.) Om vi har en ljusblixt vid t=0 från origo och ut i alla riktningar (x och y), kommer den att representeras av en växande cirkel som mappar ut en kon (Future Light Cone). Nyckelord: relativitetsteorin, speciella [45]; Kraft-Rörelse [19394] Svar: Det är mycket stora skillnader mellan SR och AR. SR är matematisk mycket enkel (algebra). AR är matematiskt mycket svår (tensorkalkyl). Teorierna behandlar vitt skilda objekt: SR elementarpartiklar/atomer och AR astronomiska objekt och universum. Utgångspunkten för SR är relativitet och ljushastighetens konstans, för AR ekvivalensen mellan gravitation och acceleration. Se vidare Theory_of_relativity#Two-theory_view Nyckelord: relativitetsteorin, allmänna [33]; relativitetsteorin, speciella [45]; 1 http://www.svd.se/infallet-som-krokte-tiden-och-rummet/om/kultur:under-strecket Kraft-Rörelse [19070] 1. myoner bildas på en höjd ca 10 km ovanför jordytan. de är instabila och sönderfaller efter en viss tid. denna tid är i laboratorium uppmätt till 2 microsekunder. på denna tid kan man tycka att de bör maxiamlt ha hunnit sträckan c*t=600m. de borde i så fall inte hinna ner till jorden. men vid markytan kan man detektera ett märkbart flöde av myoner. redogör varför! 2. en vän till dig hävdar att relativitetsteroi bara är fantasier och om det ändå vore sant så skulle man inte kunna använda det till något. vad säger du till vännen? för fram dina argument! 3. en tvilling gör en resa med ett rymdksepp som rör sig nära ljusets hastighet. han återvänder hem yngre än sin tvillingsyster som varit kvar på jorden. kan han komma tillbaka innan systern är född? jag hoppas ni kan hjälpa mig för jag fattar inget angående relativitesteteroi :S Svar: 2 Det finns massor av bevis för relativitetsteorierna. Frågan ovan och GPS (fråga 14685 3 Nej, då skulle du inte vara född heller, och du skulle ha färdats bakåt i tiden. Det är inte möjligt enligt den speciella relativitetsteorin, men möjligen tillåtet enligt den allmänna relativitetsteorin genom att tillverka något som kallas maskhål. Maskhål, spekulativa fenomen inom relativitetsteorin som skulle skapas i par och bilda genvägar genom rumtiden. Till skillnad från svarta hål, så bildas inte maskhål genom naturliga processer. De måste matas med negativ energi. Negativ energi gör att maskhålets hål håller sig öppet. Utan negativ energi upphör hålet att existera. Se länk 1 om tidsresor samt Wormhole Nyckelord: relativitetsteorin, speciella [45]; relativitetsteorin, allmänna [33]; 1 http://news.nationalgeographic.com/news/2005/09/0916_050916_timetravel.html Kraft-Rörelse [18504] Svar: Om du rör dig snabbt mot jorden så måste du ta hänsyn till den speciella relativitetsteorin. Den säger i själva verket att du uppfattar att tiden går långsammare på jorden. Ännu värre är att jordinnevånarna tycker att tiden på rymdsskeppet går långsammare. Hur är det möjligt? Vi får ta till en analogi: Adam och Beda står på en fotbollsplan 100 m ifrån varandra. Adam uppfattar Beda som liten, och Beda uppfattar Adam som liten. Detta är emellertid inget problem för någon av dem eftersom de är vana vid perpektiveffekter: föremål långt borta ser små ut. Se vidare Time_dilation Nyckelord: relativitetsteorin, speciella [45]; tidsdilatation [6]; Partiklar [18067] Ursprunglig fråga: Svar: En av forskningsgrupperna på CERN (OPERA-kollaborationen) har mätt löptiden hos neutriner från CERN till gruvan Gran Sasso 73 mil ner i Italien. Totalt har man detekterat c:a 16000 neutriner. Resultatet är att man får en hastighet som är lite överstigande ljushastigheten i vakuum c. Resultatet är signifikant med 6 standardavvikelser. Löpsträckan på 73 mil (löptid 2.4 millisekunder med ljushastigheten) bestämdes med GPS med en precision på 20 cm. Tidssynkroniseringen gjordes även den med GPS och hade en precision av 1 ns. Totala osäkerheten i tidsdata uppskattades till 10 ns, och den uppmätta effekten var 60 ns. Denna diskrepans på 60 ns motsvarar t.ex. ett fel i avståndsmätningen på 60*10-9*3*108 = 18 m. Vad gäller mätningen av löpsträckan var den största svårigheten att mäta sträckan inne i tunneln i gruvan Gran Sasso - GPSen fungerar dåligt under 1400 m berg! Man kan i mätningarna (som pågått sedan 2009) tydligt se effekter av kontinentaldriften och ett hopp i samband med en jordbävning i Italien 2009, se nedanstående figur. Man gav ett webbseminarium från CERN fredagen den 23 aeptember 2011, länk 2. Där presenterade man resultatet och metoderna mycket bra och detaljerat. Kommentarer: * De flesta fysiker tror nog att mätningen är felaktig, men än så länge finns ingen bra förklaring. Troligaste orsaken är att sträckan är felmätt eller att tidssynkroniseringen CERN-Gran Sassio är felaktig. * Einsteins speciella relativitetsteori förbjuder inte expicivt att partiklar rör sig med överljushastighet. Vad den förbjuder är att en partikel accelereras upp till ljushastigheten, det skulle kosta oändlig energi. Enda problemet är att partiklar som rör sig snabbare än ljuset (hypotetiska partiklar som kallas tachyoner, se Tachyon * OPERA-kollaborationen har helt följt god vetenskaplig procedur: * Det är inte första gången man försökt mäta neutriners hastighet, men man har inte fått fram definitiva värden. Den enda signifikanta observationen hittills är neutriner från supernovan SN 1987A, se fråga 125 (60*10-9/2.4*10-3)*168000 = 4.2 år före ljuset. Neutrinerna skulle alltså kommit fram flera år innan supernovan upptäcktes, inte några timmar. Tyvärr var neutrinodetektorerna inte igång då (Kamiokande II började ta data 1985, se (Kamioka_Observatory _____________________________________________________________________ Fotnot: Nedanstående meddelande distribuerades i samband med pressreleasen. Det får anses helt unikt att en officiell deklaration från CERN går ut tillsammans med en pressrelease. As usual, I am sending you this CERN press release before we issue it
to the media. Unusually this time, however, I feel that it needs a few
words of introduction. The OPERA collaboration has measured the time
of flight of neutrinos sent from CERN to Gran Sasso, along with the
distance they cover. These measurements appear to show that the
neutrinos are travelling faster than light. When a collaboration makes
a surprising observation such as this and is unable to account for it,
the ethics of Science demand that the results be made available to a
wider community, to seek scrutiny and to encourage independent
experiments. That's why when the spokesperson of the OPERA
collaboration asked me whether they could hold a seminar here, I said yes. Given the potential impact of such a measurement, I felt it important for CERN formally to make its position clear. That's the reason for the cautiously worded statement we're sending to the media today. Best regards, Rolf Heuer Se även Hade Einstein fel? Nyckelord: relativitetsteorin, speciella [45]; neutrino [19]; ljushastigheten [24]; nyheter [11]; SN 1987A [4]; 1 http://press.web.cern.ch/press/PressReleases/Releases2011/PR19.11E.html [18023] Tack för att ni svarade min förra fråga på ett tillfredsställande sätt. Här är en annan tankenöt jag har grubblat på: Tänk er två positiva laddningar på ett tåg som åker mycket fort. Enligt min gymnasielärare så kommer två laddningar som rör sig parallellt med varandra att vid en viss hastighet att röra sig mot varandra. Dock ur, säg en passagerares perspektiv, så stöter ju laddningarna ifrån varandra enligt Coulombs lag. Min lärare nämnde också att både passageraren på tåget och åskådaren hade rätt om laddningarnas läge, även fast de motsade varandra. Hur är detta möjligt? MVH Adam Svar: Din nya fråga är betydligt svårare, så jag fick fråga en expert på KTH i Stockholm. Här är hans svar: Man kan nu tycka att två laddningar på ett tåg skulle ge en elektrisk ström och alltså attrahera varandra, men som du påpekar blir detta paradoxalt då man ju kan transformera sig till vilosystemet (tåget) och där finns ingen ström och inga magnetfält utan bara elektrostatisk repulsion. Detta är ett subtilt problem som jag inte har sett särskilt mycket diskussion av i läroböcker, eller annorstädes heller för den delen. Problemet finns alltid när man bara ser till laddningar av ett tecken. Verkligheten är dock elektriskt neutral och har man två laddningar koncentrerade så finns det en motsatt lika stor laddning någonstans. En invariant ström (ström som är oberoende av observatörens hastighet) får man bara när man har relativ rörelse av positiva och negativa laddningar. Den "riktiga" elektriska strömmen ges alltså av relativ rörelse för laddningar av två olika tecken. Om de två laddningarna på tåget kompenseras av lika stor laddning av motsatt tecken som också följer med tåget har man ingen verklig (invariant) ström och fenomenet uteblir. Om däremot den motsatta laddningen är i vila (utanför tåget) så har man relativ rörelse av laddning och invariant ström. Då får man den magnetiska attraktionen som för ihop laddningarna. Så ser i alla fall jag på saken. Hanno Essén
Det är alltså en känt besvärlig fråga. I Wikipedia-artikeln Relativistic_electromagnetism Tack Hanno för hjälp med svaret! Nyckelord: relativitetsteorin, speciella [45]; magnetism [52]; Elektricitet-Magnetism, Materiens innersta-Atomer-Kärnor [17654] Ursprunglig fråga: Svar: Som alltid vill jag emellertid varna för modellen att elektronerna är små laddade kulor som snurrar i banor kring kärnan och riskerar falla ner i densamma, se fråga 13733 För att "förstå" atomära system löser man en ekvation, schrödingerekvationen (SE), se Schrödinger_equation SE tar inte hänsyn till relativistiska effekter, t.ex. att en elektrons massa beror av dess hastighet (speciella relativitetsteorin). Diracekvationen (Dirac_equation Artikeln från Uppsala universitet (länk 2 är en light-version, originalartikeln är bitvis rätt svår att förstå för icke-specialister) redovisar en beräkning av energinivåerna i bly både icke-relativistiskt och relativistiskt. Man kan med den relativistiska lösningen mycket bra reproducera EMS (fråga 17476 För tenn (som ligger ovanför bly i det periodiska systemet och borde likna bly) är den relativistiska effekten mycket mindre, vilket medför att tennbatterier är ganska värdelösa eftersom EMS är mycket liten. Anledningen är att tenn har betydligt lägre kärnladdning än bly (50 respektive 82), vilket innebär att elektronerna rör sig långsammare i tenn. Det visar sig från räkningarna att det är framför allt 6s nivåerna (6s är bland valens-nivåerna i bly) som påverkas av relativistiska effekter. Eftersom s motsvarar rörelsemängdsmomentet 0 har dessa elektroner en liten men dock sannolikhet att befinna sig nära atomkärnan. På grund av blys höga kärnladdning rör de sig då mycket snabbt, och relativistiska effekter blir stora. Ökningen i elektronens massa gör att orbitalen krymper och fördelningen hos elektronmolnet förskjuts in mot kärnan. Sammanfattningsvis beror effekten på att relativistiska effekter för elektroner nära blykärnan påverkar valensnivåerna, vilka i sin tur bestämmer EMS för blybatteriet. Jag tycker artikeln är intressant av flera skäl: Den relativistiska kontraktionen av 6s orbitalen förklarar även varför guld glimmar gult och varför guld är så lite reaktivt: What Gives Gold that Mellow Glow? Slutligen kan jag inte låta bli att citera den avslutande meningen i artikeln: Finally, we note that cars start due to relativity Nyckelord: kvantmekanik [30]; batteri [25]; relativitetsteorin, speciella [45]; 1 http://www.unt.se/uppsala/kravs-en-einstein-for-att-starta-bilen-1220168.aspx Kraft-Rörelse [17609] Svar: Viloenergin E0=m0c2 kan göras troligt från uttrycket för relativistisk massa, se fråga 14250 Om man antar att totala energin E beror av m och c kan man se genom en dimensionsanalys att E=mc2: Energin E i vänsterledet har dimensionen J. Högerledet har dimensionen kg*(m/s)2 = kg*m/s2*m = N*m = J Exponenten för m måste alltså vara 1 och exponenten för c vara 2 för att dimensionerna skall stämma. c2 har inget att göra med att något rör sig. c2 i detta sammanhanget är bara som vilken naturkonstant som helst, t.ex. Newtons gravitationskonstant G, se fråga 12834 Nyckelord: relativitetsteorin, speciella [45]; Värme [17491] Svar: Låt oss räkna på en kulstötningskula. Den väger 7.26 kg (Kulstötning För att värma upp kulan från 20 grader till 100 grader krävs energin DQ = 7.26*449*80 = 2.6 105 J Från E = mc2 får vi massdifferensen Dm = 2.6 105/(3 108)2 = 2.9 10-12 kg vilket torde vara omätbart! Se vidare Special_relativity#Equivalence_of_mass_and_energy Nyckelord: relativitetsteorin, speciella [45]; specifik värmekapacitet [25]; Materiens innersta-Atomer-Kärnor [17237] Ursprunglig fråga: Svar: Oskar kom tillbaka med följande fråga: Jag har försökt bli klok på varför man inte kan bestämma elektroners exakta position och varför de inte kan befinna sig i atomkärnan enligt Heisenbergs obestämdhetsrelation, men jag begriper mig inte på den. Kan ni förtydliga vad det egentligen obestämdhetsprincipen säger? Oscar! Det var det konventionella svaret du fick, och jag håller med att jag kunde varit lite tydligare. Så låt oss först räkna lite. Obestämdhetsrelationen ges av (Heisenberg_uncertainty_principle Dx*Dpx = h/4p (1) Om vi stänger in en elektron i en atomkärna så är Dx ungefär 10-15 m. Vi får då Dp = 0.5*10-34/10-15 J*s/m = 0.5*10-19 N*s För att få en bättre uppfattning om vad detta betyder gör vi om rörelsemängd p till energi E. Det relativistiska sambandet är (vi måste använda relativistiska samband eftersom hastigheten är hög) E2 = (pc)2 + (mc2)2 (2) Eftersom energin kommer att visa sig vara mycket hög så kan vi försumma elektronens viloenergi mc2 och får det enkla sambandet E = pc (3) (Detta är för övrigt även sambandet mellan energi och rörelsemängd för en foton.) Vi får E = 0.5*10-19*3*108 N*s*m/s = 1.5*10-11 J = 1.5*10-11/(1.602*10-13) MeV = 100 MeV. För det första kan vi konstatera att det var OK att försumma vilomassan för elektronen (0.511 MeV). För det andra ser vi att detta är en mycket hög energi och vi känner ingen kraft som är stark nog att hålla elektronen fångad. Coulombkraften räcker inte till på långa vägar - den ger det lägsta tillståndet (1s) i en atom på medelavståndet 10-10 m, vilket är fem storleksordningar större än atomkärnans utsträckning. Små system som atomer och kärnor följer alltså inte de lagar vi är vana vid i vardagen. Två olika laddade klot attraherar varandra och kommer att fastna vid varandra. Elektroner följer emellertid kvantmekanikens lagar och måste bland annat lyda Heisenbergs obestämdhetsrelation. Det är emellertid inte helt lätt att tolka vad kvantmekaniken säger oss om naturen. Se t.ex. Kvantmekanik#Exempel_p.C3.A5_tolkningar De flesta fysiker föredrar Köpenhamnstolkningen. Den sista, lite skämtsamma, "håll käft och räkna!" är inte heller så dum. Även om kvantmekaniken är svårförståelig så stämmer resultatet mycket bra med observationerna, och det är det viktigaste för en fysikalisk teori. Länkarna 1 och 2 är svar på liknande frågor. Man kan även resonera på ett annat sätt: om man stänger in elektronen i en låda om 2*10-15 m så måste våglängden vara högst 4*10-15 m (vågen måste ha en nod där potentialen blir oändlig). Vi får rörelsemängden p = h/l = 6.6 10-34/4 10-15 = 2 10-19 N*s vilket är av samma storleksordning som ovan. Nyckelord: Heisenbergs obestämdhetsrelation [12]; kvantmekanik [30]; relativitetsteorin, speciella [45]; 1 http://www.newton.dep.anl.gov/askasci/chem99/chem99283.htm Kraft-Rörelse [17098] Svar: Maskhål i den allmänna relativitetsteorin skulle möjligen tillåta riktiga tidsresor, men man får problem med orsak och verkan. Tänk om du vid en tidsresa orsakade något som skulle märkas i din egen tid. T.ex. att din far och mor aldrig träffades! Sedan är den speciella relativitetsteorin en beskrivning av likformig rörelse (utan acceleration) medan den allmänna relativitetsteorin är en beskrivning av gravitationen. Teorierna har alltså mycket lite med varandra att göra. Nyckelord: relativitetsteorin, speciella [45]; relativitetsteorin, allmänna [33]; Kraft-Rörelse [16270] Som jag ser det så skulle det för någon som befinner sig på något utav tågen bara se ut som att det snabba tåget åkte ifrån det första, men enligt tidsdilatationen så stämmer väl inte det? Från ett utomstående system måste väl det långsammare tåget som inte tidsdilatationeras lika mycket krocka, eller passera igenom det första tåget... Något som känns otroligt. Fast det gör ju å andra sidan ganska mycket när man pratar relativitet. Svar: Se även fråga 16263 Nyckelord: relativitetsteorin, speciella [45]; Kraft-Rörelse [16263] Jag tror att jag har hittat en paradox när jag började räkna lite grann på tidsdilatationen. För det första; Om man skulle befinna sig på ett tåg som rörde sig med en hastighet av 0.9999c under fem minuter, så skulle det för en utomstående observatör ha gått ca fem timmar, enligt t0=t/(sqrt(1-(v^2/c^2)) där t0 är observatörens tid, och t är tiden för personen på tåget. t0=t/(sqrt(1-(v^2/c^2)) för t = 300s =>
300/(sqrt(1-.9999^2) = 21 213.7338s ~ 5 timmar om vi sedan släpper iväg ett tåg med halva hastigheten på samma sträcka, så skulle det ta 600s att färdas samma sträcka. Det leder till en tidsdilatation på 600 / sqrt(1 - (.49995^2)) = 692.797231 Alltså inte mer än 1.5 minuter! Det betyder att för en utomstående observatör så skulle det långsammare tåget komma fram flera timmar före det snabbare! Hur kan man förklara detta?
---- När jag tänkte lite på detta kom jag fram till ytterliggare en fråga, nämligen att ett ljusår (eller ljusminut, eller vilken annan avståndsbenämning som helst som bygger på ljushastigheten) ju är ett begrepp som är äldre än relativitetsprincipen. Betyder det att tidsdilatation inte tagits med i beräkningen av sträckan? För om så är fallet leder samma ekvation som tidigare till att en sträcka på 8 ljusår (jorden / sirius) skulle vara byggt på en tidsdilationerad bild av ljuset. Om man med samma tåg som tidigare åkte med en hastighet av 0.9999c så skulle man behöva färdas i endast en vecka för att tiden skall dilatationeras åtta år. Hur går det ihop? --- Frågan framför allt, vad har jag missat; jag tror knappast att jag hittat ett otäppbart hål i grunden för den moderna fysiken. Tack. Svar: Låt oss först reda ut var ditt resonemang går fel och sedan lite om hur man skall uppfatta en fysikalisk teori och då speciellt relativitetsteorin. I ditt första resonemang använder du dig av begreppet samtidighet, se fråga 3061 nedan och Relativity_of_simultaneity Din andra fråga har egentligen inget med relativitetsteorin att göra. Ett ljusår är en sträcka som ljuset tillryggalägger på ett år sett utifrån slutpunktens referensram. Ljushastigheten har varit känd med tillräcklig precision ganska länge, så det är inget problem att förvandla km till ljusår. En observatör som rör sig i förhållande till denna referensram kommer visserligen att ha en avvikande uppfattning om avståndet (längdkontraktion), men det förändrar inte det "verkliga" avståndet. Den speciella relativitetsteorin utgår från två antaganden: 1 Naturlagarna är oberoende av rörelse med konstant hastighet 2 Ljushastigheten i vakuum c är densamma oberoende av observatörens rörelse Dessa antaganden är rimliga med hänsyn till observationer, men de går inte att bevisa. Detta är en metod man ofta använder i vetenskapen: gör ett antagande och visa vad antagandet innebär vad gäller fenomen man kan observera. Om observationen skiljer sig från vad man väntat har man falsifierat teorin, och man får göra nya antaganden. Man har inte falsifierat relativitetsteorin, utan alla observationer stämmer med vad man väntar med utgångspunk från de två antagandena. Detta är typiskt för naturvetenskapliga teorier: det går aldrig att bevisa att de är korrekta - endast att de är inkorrekta. De inkorrekta sorteras bort och lagras i vetenskapshistoriens skräpkammare. De som överlever blir, allteftersom nya typer av observationer visar sig stämma, mer och mer etablerade. Einsteins speciella relativitetsteori tillhör de mest etablerade fysikaliska teorierna. Ibland kan steget mellan att formulera antagandena för en teori och att visa på vad teorin förutsäger vad gäller observationer vara svårgenomträngligt för en experimentalfysiker. Då får vi helt enkelt lita på att teoretikerna kan sin sak och att de formler de får fram är korrekta. Den speciella relativitetsteorin ställer rimliga krav på matematikkunskaper - relativt enkel algebra räcker. Svårigheten är att vissa av resultaten av teorin står i strid med intuitionen. Den allmänna relativitetsteorin (se General_relativity Är då relativitetsteorierna de slutgiltiga teorierna? Nej, det är de inte, vi saknar bland annat en förening med kvantmekaniken. En ny teori kommer att omfatta relativitetsteorierna men utökas till att även ta hänsyn till kvantmekaniska fenomen. Det finns en mycket omfattande och bra artikel i engelska Wikipedia: Special_theory_of_relativity Se även fråga 3061 Nyckelord: relativitetsteorin, speciella [45]; fysik, förståelse av [17]; relativitetsteorin, allmänna [33]; Kraft-Rörelse [15804] Svar: Wikipedia-artikeln Faster-than-light Nyckelord: relativitetsteorin, speciella [45]; ljushastigheten [24]; 1 http://www.telegraph.co.uk/earth/main.jhtml?xml=/earth/2007/08/16/scispeed116.xml Kraft-Rörelse [14912] Och hur vet man ens att objektet som accelereras för observatören krymper i längriktningen och att det inte ökar i längdriktningen för resenären istället? Teoretiskt sätt liksom, Einstein kom väl på det här långt innan några praktiska experiment var gjorda? Svar: Se även fråga 12892 Nyckelord: relativitetsteorin, speciella [45]; 1 http://faraday.physics.utoronto.ca/PVB/Harrison/SpecRel/Flash/ContractInvisible.html Kraft-Rörelse [14685] Ursprunglig fråga: Svar: Det universiella navigeringssystemet GPS (se Global_Positioning_System Dels orsakar banrörelsen att den mycket exakta klockan i en satellit saktar sig 7 mikrosekunder per dygn pga den speciella relativitetsteorin. Eftersom satelliten befinner sig i ett svagare gravitationsfält går klockan 45 mikrosekunder per dygn snabbare. Nettokorrektionen 45-7=38 mikrosekunder per dygn appliceras genom att man justerar klockan att gå lite långsammare innan satelliten skickas upp. Man synkroniserar även alla klockorna med hjälp av klockor på marken. Se vidare länk 1. Se vidare Special_relativity Tillägg 5/4/2011: Uppskattning av effekterna Konstanter: Speciell relativitet Vi räknar från jordens centrum eftersom satelliterna går ganska högt och jordens rotationshastighet är liten (mindre än 500 m/s) jämfört med satelliternas hastighet. Satellitens hastighet v ges av mv2/RGPS = mMG/(RGPS)2 vilket blir v = sqrt(MG/RGPS) = sqrt(5.97*1024*6.67*10-11/(26.367*106) = 3886 m/s Klockan påverkas med g-faktorn (Special_relativity#Time_dilation_and_length_contraction g = sqrt(1-(v/c)2) =
sqrt(1-(3886/300000000)^2) = 0.9999999999161055 Den relativa korrektionen blir 1 - g = 8.389*10-11 och korrektionen på ett dygn blir 8.389*10-11*60*60*24 = 7.25*10-6 s eller c:a 7 mikrosekunder. Allmän relativitet Denna korrektion har att göra med att man måste bevara totala energin även i ett gravitationsfält, se fråga 16989 Om gravitationspotentialen är U(r) så gäller genom integration av gravitationskraften U(r) = -mMG/r Ändringen i potentiell energi om vi går från jordytan till satellitbanan blir DU = -mMG/RGPS -(-mMG/R) = -mMG(1/RGPS -1/R) Med insatta värden blir DU = m*4.714 107 Om vi dividerar detta med viloenergin mc2 får vi den relativa korrektionen till 5.237 10-10 På ett dygn blir korrektionen 5.237 10-10*24*60*60 s = 45.2 mikrosekunder vilket stämmer bra med värdet ovan. Nyckelord: relativitetsteorin, allmänna [33]; GPS [3]; relativitetsteorin, speciella [45]; 1 http://www.astronomy.ohio-state.edu/~pogge/Ast162/Unit5/gps.html Kraft-Rörelse [14500] Svar: Länk 1 är en trevlig framställning av olika aspekter på relativitetsteori av Frank Borg. Fler artiklar finns under länk 2. Nyckelord: Newtons rörelselagar [21]; relativitetsteorin, speciella [45]; 1 http://fragelada.fysik.org/resurser/relativ.pdf Kraft-Rörelse [14250] Svar: Däremot är det inte så svårt att se att det relativistiska uttrycket reduceras till det klassiska uttrycket för kinetisk energi för små hastigheter v (b=v/c): Totala energin, E = m0c2/(1-b2)1/2 (1) Om vi Taylorutvecklar nämnaren och tar med bara de första två termerna får vi E = m0c2 + (1/2)*m0c2*v2/c2 = m0c2 + (1/2)*m0v2 (2) Vilket är viloenergin + det klassiska uttrycket för rörelseenergin. Se vidare Relativistic_mass Nyckelord: relativistiskt massberoende [4]; relativitetsteorin, speciella [45]; Kraft-Rörelse [13654] Svar: Om vi utifrån observerar periferin på cylindern, så kommer vi att finna att denna utsätts för längdkontraktion. Omkretsen blir alltså mindre. Å andra sidan är det klart att radien på cylindern inte påverkas eftersom rörelsen i ytterkanterna är riktad mot eller från betraktaren. p definieras ju som omkretsen av en cirkel dividerat med 2*radien. Eftersom omkretsen blir mindre men radien inte ändrar sig, kommer vi att få ett mindre värde på p än det vanliga. Detta beror på att rummet är krökt - en fundamental konsekvens av den allmänna relativitetsteorin.
Nyckelord: relativitetsteorin, speciella [45]; Blandat [13642] Svar: Nyckelord: lorentztransformation [2]; relativitetsteorin, speciella [45]; Ljud-Ljus-Vågor [13218] Svar: Att c är konstant oberoende av källans eller mottagarens rörelse är ett postulat (fundamentalt antagande) i Einsteins speciella relativitetsteori. Einstein grundade antagandet på resultatet av ett experiment där Michelson-Morley försökte påvisa etern. Etern vad det medium man trodde transporterade elektromagnetisk strålning. Resultatet av M-M försök var att de inte såg någon skillnad på olika riktningar trots att jorden rör sig i sin bana med en hastighet av 30 km/s. M-M tolkade resultatet så att jordens rörelse genom etern "tryckte ihop" jorden, så att det inte blev någon skillnad. Se vidare Michelson-Morley Experiment Einstein omtolkade resultatet av M-Ms experiment så att han i stället antog att c är konstant oberoende av källans eller mottagarens rörelse. Från detta antagande härledde han en teori - den speciella relativitetsteorin - som i nästan 100 år visat sig stämma exakt med alla mätningar. Ljushastighetens konstans kan alltså anses väl etablerad. Så etablerad att den internationella unionen för mått och vikt 1983 antog en ny definition av längdenheten meter, enligt vilken en meter är den sträcka som ljuset tillryggalägger i tomrum på 1/299 792 458 sekund. Därmed är ljushastigheten i vakuum definierad till exakt 299 792 458 m/s. Se vidare Is The Speed of Light Constant? M-Ms experiment med interferometrar i två vinkelräta riktningar visar (om man tolkar det så) att ljushastigheten är oberoende av mottagarens rörelse. Om man noggrannt observerar hur dubbelstjärnor rör sig i sina banor kan man även visa att ljushastigheten är oberoende av källans rörelse. Så som du ser var det ingen lätt fråga du ställde Fotnot: Experiment att bestämma ljushastigheten som är lätt att förstå men kräver lite utrustning finns i länk 1 nedan. Se även fråga 3545 Nyckelord: elektromagnetisk strålning [21]; ljushastigheten [24]; relativitetsteorin, speciella [45]; #ljus [63]; Kraft-Rörelse [12892] Svar: Tidsdilatationen bekräftas av det faktum att vi observerar myoner vid jordytan, se fråga 2697 nedan. Nedanstående animering visar hur tidsdilatationen uppkommer. Ländkontraktionen (Lorentz-Fitzgerald kontraktion) är lite svårare att observera direkt, se länk 2 nedan. Den följer emellertid av relativitetsteorin, som är väl etablerad med andra observationer (se ovan). Den är emellertid kopplad till tidsdilationen. Föreställ dig myonerna som nämndes ovan. Sett i myonens koordinatsystem går tiden som vanligt, och myonen borde alltså sönderfalla innan den når jordytan. Motsägelsen försvinner om vi tar hänsyn till längdkontraktionen: sträckan myonen behöver tillryggalägga är mycket kortare pga längdkontraktionen. Nedanstående animering förklarar längdkontraktionen. Det finns massor med böcker om relativitetsteori och mycket på webben. Relativitetsteori - Resurser Animeringarna är gjorda av David M. Harrison, Dept. of Physics, Univ. of Toronto, se länk 1. Se även fråga 2697 Nyckelord: tidsdilatation [6]; relativistiskt massberoende [4]; längdkontraktion [6]; relativitetsteorin, speciella [45]; 1 http://www.upscale.utoronto.ca/PVB/Harrison/Flash/ Kraft-Rörelse [12742] 1 Hur långt är det mellan Sthlm & Malmö sett från rymdskeppet? 2 Hur långt tid tar det att resa mellan Sthlm och Malmö sett från rymdskeppet? 3 Hur långt tid tar samma resa sett från jorden? Skulle vara tacksam för svar.
Jag har fått fram några tankar själv men det är svårt. Svar: A och O är att inte blanda ihop koordinaterna för det rörliga och fixa systemet i Lorentztransformationen. Observera emellertid att du är fri att välja vilket system som är rörligt och vilket som är fixt. Låt koordinater med ' vara i rymdskeppet, koordinater utan ' på marken. Båda är överens om den relativa hastigheten v=0.95c (annars skulle inte relativitetsprincipen gälla). 1 Använd lorentzkontraktionen: l' = l/g där g = (1-v2/c2)-1/2. Eftersom g > 1 blir l' mindre än l. 2 Tidsdilatationen ger: t' = l'/v = l/g*v = t/g. Eftersom g > 1 blir t' mindre än t - tiden går långsammare. 3 t = l/v Observera emellertid att den relativa hastigheten är samma i båda systemen: v = l'/t' = l/g/t/g = l/t Nyckelord: tidsdilatation [6]; längdkontraktion [6]; relativitetsteorin, speciella [45]; 1 http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/tdil.html#c1 Kraft-Rörelse [12753] Ursprunglig fråga: Hur kom Einstein på formeln E=mc2? Var det en slump, eller inte?
(Henrik A) Fungerar alltid Einsteins formel E=mc2? Vad använder man den till? (Erik D) Svar: Det är svåra frågor ni ställer eftersom ni vill veta det historiska perspektivet. Det är en hel vetenskap som heter vetenskapshistoria, och det är vi inte experter på. Jag skall emellertid försöka mig på ett par kommentarer. Relativitetsteorin publicerades av Einstein 1905. Här är originalversionen: Zur Elektrodynamik bewegter Körper Relativitetsteorin bygger i stort på ett antagande:
att ljushastigheten c i vakuum är konstant oberoende av hur man rör sig i förhållande till ljusstrålen. Antagandet bygger på ett experiment som utfördes av Michelson-Morley 1887: History of Special Relativity Länk 1 nedan är Einstein själv som förklarar vad formeln innebär. Här är en artikel som ger ett par olika härledningar: Year of Physics 2005 Exakta mätningar som bekräftade relativitetsteorin kom betydligt senare. Inte ens nobelkommittén var imponerad: nobelpriset Einstein fick 1921 var för hans förklaring av den fotoelektriska effekten (också 1905) och inte relativitetsteorin! Tolkning: Ekvationen E=mc2 skall tolkas så att massa och energi är ekvivalenta (utbytbara mot varandra) med "växlingskursen" c2. Eftersom c är ganska stort motsvarar även en liten massa (eller mass-skillnad) en mycket stor energi. Bekräftelsen på E=mc2 kom först på 20/30-talet när man kunde mäta atommassor med hög precision, se fråga 12726 Det finns många böcker om relativitetsteorin och en bra artikel i Nationalencyklopedin Se även fråga 20460 Nyckelord: Einstein, Albert [1]; relativitetsteorin, speciella [45]; Kraft-Rörelse [12597] Jag har läst att Einstein ansåg att all materia rör sig i ljusets hastighet uppdelat i tre rumsdimensioner och en tidsdimension. Ju snabbare genom rummet man rör sig ju långsammare genom tiden. Eftersom inget förutom ljuset kan röra sig i ljusets hastighet bör det betyda att att rörelse genom rummet ej kan ske om inte den kompletteras med en rörelse genom tiden. Står tiden stilla kan inte en rörelse genom rummet noteras. Men varför gäller detta inte ljuset? Varför ser vi att ljus rör sig trots att tiden står stilla för ljuset enligt oss?
Vad är det jag har missat? Svar: Den rörliga observatören (egentligen kan man inte skilja på observatörerna, men antag att den ena observatören är på jorden och den andra i en raket) ser den tillryggalagda stäckan mycket förkortad - lorentzkontraktion. Den stationära observatören tycker att tiden i det rörliga systemet går mycket långsammare - tidsdilatation. Resultatet blir då att de ändå är överens systemens relativa hastighet. Rörelse är ju tillryggalagd sträcka på en viss tid, så rörelse utan tid är meningslös. Apropå speciella relativitetsteorin, här är en klassisk limerick:
There was a young Lady named Bright,
- A. H. Reginald Buller (1874-1944) Se även fråga 10432 Nyckelord: relativitetsteorin, speciella [45]; Blandat [12459] Allting är väldigt förvirrat. Tacksam för svar! Svar: Se även länk 2 och Twin_paradox Nyckelord: tvillingparadoxen [5]; relativitetsteorin, speciella [45]; fysik, förståelse av [17]; 1 http://www.upscale.utoronto.ca/PVB/Harrison/Flash/ Kraft-Rörelse [11073] Svar: Bilar och cyklar blir hoptryckta (längdkontraktion) och rödljusen blir gröna (dopplerförskjutning). Delar av boken på engelska finns under länk 1. Länk 2 innehåller en utökad version (även Gamows andra bok om Mr Tompkins). Se även Mr_Tompkins Nyckelord: relativitetsteorin, speciella [45]; kvantmekanik [30]; 1 http://boomeria.org/physicslectures/secondsemester/relativity/tompkins.html Kraft-Rörelse [9324] Nu undrar jag vilka andra fenomen som den klassiska fysiken inte kunde förklara,
fick sina förklaringar genom Einsteins eminenta teorier? Vore tacksam för svar. Svar: Den viktiga skillnaden är, att Einstein utgår ifrån, att ljushastigheten i
vakuum är konstant och oberoende av inertialsystemet. Vidare utgår han
ifrån att energi och information inte kan förflytta sig snabbare
än ljuset.
Det leder till att
begrepp som tid, längd och samtidighet inte fungerar enligt vår
vardagsuppfattning. Det leder också till den välkända relationen
mellan energi och massa
E = mc2. Den allmänna relativitetsteorin är huvudsakligen en gravitationsteori,
baserad på den speciella relativitesteorin. Här inför man
ekvivalensprincipen, som säger att den tunga massan är lika med den
tröga massan. Den första har med gravitation att göra, den andra med
acceleration. Gravitationskraften (liksom centrifugalkraften) betraktas
här som en fiktiv kraft, alltså en kraft som egentligen inte behövs.
Partiklar som inte påverkas av någon kraft, rör sig "rätlinjigt" i den
krökta fyrdimensionella rumstiden. En satellit som rör sig i en bana
runt jorden, rör sig i någon mening "rätlinjigt" i den rumstid, som
kröks av jordens massa. Att gå in på alla fenomen, som förklaras av Einsteins teorier skulle dra
alldeles för långt. Man kan i alla fall konstatera, att inga exerimentella
data strider mot teorierna. Sedan vill vi påpeka, att man inte kan säga
att Newtons mekanik är fel. Under mindre extrema förhållanden duger
den utmärkt. När man skickar sonder till Mars, använder man Newtons mekanik. Nyckelord: massa, trög/tung [4]; relativitetsteorin, allmänna [33]; relativitetsteorin, speciella [45]; Kraft-Rörelse [7306] Svar: Nyckelord: relativitetsteorin, speciella [45]; Kraft-Rörelse [2697] Svar: Först ett par definitioner: Längdkontraktion är den minskning i längd som enligt Albert Einsteins speciella relativititetsteori uppstår när ett föremål rör sig med stor hastighet i förhållande till den som mäter längden. Vid mer vardagsnära hastigheter är denna längdminskning helt försumbar. Det är först vid hastigheter som är minst 1/10 av ljusets hastighet som den får någon märkbar betydelse. Tidsdilatation (tidsutvidgning) beroende på hastighet innebär att om två referenssystem r och r', har identiska klockor, kommer en observatör i r att anse att klockan i r' går långsammare om referenssystemen r och r' befinner sig i relativ rörelse. En observatör i r' anser likaså att klockan i r går långsammare än den lokala klockan. Kosmiska strålningen består huvudsakligen av atomkärnor med mycket höga energier (mest väte). När de kolliderar med luften på cirka 20 km höjd, uppstår en uppsjö av olika partiklar. De flesta är kortlivade och sönderfaller snabbt. En av sönderfallsprodukterna kallas myon, och på grund av sina egenskaper, är den mycket lite benägen att kollidera med kärnorna i luften. Den försvinner för det mesta genom att den sönderfaller. Hur långt går den? Myonens medellivslängd är 2.2*10-6 s. Antag att den går nära ljushastigheten (300000 km/s). Då får vi en sträcka på 300000 * 2.2*10-6 = 0.6 km = 660 m. Ändå är det så, att de flesta partiklar vi kan registrera här nere är myoner. Genom en människa far det typiskt 30 - 40 högenergetiska myoner varje sekund. De överlever hit ner på grund av tidsdilatationen. De har så hög hastighet att tiden går mycket långsammare för dem, se översta formeln i bilden nedan. En myon med en Lorentz-faktor på 1000 kan i princip gå 660 km. Sådana myoner är inte alls ovanliga. För den myonen går tiden 1000 gånger långsammare (från oss sett). Jaha, OK men sett från myonen då? Där går ju tiden med "normal" hastighet och myonen kan väl inte hinna ner till markytan innan den sönderfaller? Jo, det gör den därför att längdkontraktionen, se nedersta formeln nedan, gör att den sträcka myonen måste tillryggalägga är mycket kortare (sett ur myonens perspektiv). Det är klart att resultatet att myonen hinner ner till marken innan den sönderfaller måste vara samma oberoende av om vi betraktar myonen från marken eller om vi följer med den ner genom luften. Se vidare Muon Se även fråga 1289 Nyckelord: relativitetsteorin, speciella [45]; längdkontraktion [6]; tidsdilatation [6]; Blandat [1074] Svar: Listan kan göras mycket längre. Läs någon av de populära böcker som finns om relativitetsteorin, till exempel "Einsteins universum" av Calder. Se även Allmän relativitetsteori och kosmologi Nyckelord: relativitetsteorin, allmänna [33]; relativitetsteorin, speciella [45]; Kraft-Rörelse [3061] Svar: Signalerna från brytarna måste ju transporteras till lampan, och
det kan ju inte gå fortare än ljuset. Beroende på vilken
transporthastighet man antar, tågets hastighet och lampans placering
får man olika resultat. Det går i varje fall att analysera situationen,
så att resultatet blir det samma, sett från tunneln och tåget. Tillägg 21/4/08: Länk 1 nedan 'The Train and The Twins' diskuterar tågparadoxen (ytligt) och tvillingparadoxen ingående. Länk 2 (Storrs McCall & E. J. Lowe: 3D/4D equivalence, the twins paradox and
absolute time) säger att tågparadoxen endast kan lösas om man betraktar problemet i full rymd-tid 4D. Problemet är en perspektiveffekt. Se även diskussion i Taylor/Wheeler: Spacetime Physics. Det finns för övrigt flera varianter av tåg-tunnelparadoxen: en linjal och lucka i bordet, en hoppstav och en lada mm. Nyckelord: relativitetsteorin, speciella [45]; tvillingparadoxen [5]; 1 http://galileoandeinstein.physics.virginia.edu/lectures/sreltwins.html Kraft-Rörelse [782] Svar: (v1+v2)/(1+v1v2/c2). För
ditt exempel v1=v2=0.6c blir resultatet 1.2c/(1+0.36)=0.88c.
Observera att om en av hastigheterna är c blir den relativa hastigheten (c+v2)/(1+c*v2/c2) = (c+v2)/(1+v2/c) = c(c+v2)/(c+v2) = c alltså summan blir aldrig högre än c. Nyckelord: relativitetsteorin, speciella [45]; addition av hastigheter [2]; ljushastigheten [24]; Frågelådan innehåller 7624 frågor med svar. ** Frågelådan är stängd för nya frågor tills vidare **
|




 .
.
 !
!
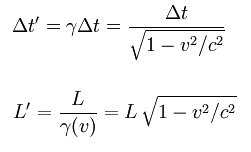
 Sök i svenska Wikipedia:
Sök i svenska Wikipedia:
