Vill du ha ett snabbt svar - sök i databasen: Anpassad Google-sökning 6 frågor/svar hittade Kraft-Rörelse [21219]
1. När man bestämmer referensram och längdkontraktion för någonting beräknar man ju fart och riktning relativt någonting annat. Betyder inte det att allting har i stort sett oändligt många referensramar och längdkontraktioner eftersom man kan jämföra fart och riktning med allt annat som har en annan fart och riktning? 2. Jag har förstått att längdkontraktion fungerar för all materia och således också elementarpartiklar. Men en elementarpartikel, som till exempel elektronen, ändrar ju riktning hela tiden. Ändras då också referensram för elektronen vid varje riktningsförändring? Det blir väl en konstant förändring? Svar: 2) Ja, även elementarpartiklar påverkas av längdkontraktionen. Man kan inte observera kontraktionen direkt, men en snabb elektron antar "pannkaksform" och detta påverkar det elektriska fältet. Se Length_contraction#Experimental_verifications Se även bilden nedan från länk 1. Den visar pannkaksformen hos kolliderande tunga joner. Se även fråga 20459 Kolliderande tunga joner antar pannkaksform på grund av längdkontraktionen: Nyckelord: längdkontraktion [6]; relativitetsteorin, speciella [45]; Kraft-Rörelse [20459] Ursprunglig fråga: Svar: Man kan göra en enkel geometriskt härledning av tidsdilationen, se nedanstående figur. Enda antagandet är att ljushastigheten c är konstant oberoende av koordinatsystemets rörelse. Vi undersöker först hur en klocka bestående av en ljusstråle som går uppåt och reflekteras av en spegel. I övre delen av figuren visas hur klockan uppför sig när den inte rör sig. I nedre delen rör sig klockan med hastigheten v. För att ljusstrålen skall komma tillbaka till samma punkt måste den färdas lite längre sträcka. Om vi tillämpar Pythagoras sats på den rätvinkliga triangeln får vi D2 = L2 + (v Dt'/2)2 (c Dt')2 =
(c Dt)2 +
(v Dt')2 Dt' sqrt(1-v2/c2) = Dt Dt' = Dt g där g = 1/sqrt(1-v2/c2) I Length_contraction#Time_dilation L' = L0 / g där L' är mindre än L0. Se även fråga 20002 Nyckelord: längdkontraktion [6]; lorentztransformation [2]; tidsdilatation [6]; 1 http://hyperphysics.phy-astr.gsu.edu/hbase/Relativ/tdil.html Kraft-Rörelse [20002] Jag har lite problem med att härleda formlerna för längdkontraktion och tidsdilation från Lorentztransformationen och undrar var jag tänker fel. Jag börjar med att introducera två godtyckliga händelser i rumtiden, (t₁, x₁, y₁, z₁) och (t₂,x₂, y₂, z₂). Vidare, för att förenkla problemet, låter jag y₁, = z₁ = y₂ = z₂ = 0. Om jag definierar metriken d_x(x2', x1') = x2'- x1' finner jag att d_x = gamma*(x2 - v*t2) - gamma*(x1 - v*t1). Om jag nu resonerar att t2 = t1 eftersom jag mäter båda händelserna vid samma tidpunkt kan jag ersätta t2 med t1 och få d_x(x2', x1') = Δx' = gamma * Δx, vilket stämmer. Men om detta görs för metriken d_t(t2', t1') = t2'- t1' och villkoret x1 = x2 får jag istället d_t(t2', t1') = Δt' = gamma * Δt, när Δt' egentligen ska vara Δt/gamma. Varför kan jag inte anta x2 = x1, och hur härleder jag formeln för tidsdilation från Lorentztransformationen annars? Svar: I artikeln Tidsdilatation Se även Längdkontraktion eller lyssna på föreläsningen Nyckelord: relativitetsteorin, speciella [45]; tidsdilatation [6]; längdkontraktion [6]; Kraft-Rörelse [12892] Svar: Tidsdilatationen bekräftas av det faktum att vi observerar myoner vid jordytan, se fråga 2697 nedan. Nedanstående animering visar hur tidsdilatationen uppkommer. Ländkontraktionen (Lorentz-Fitzgerald kontraktion) är lite svårare att observera direkt, se länk 2 nedan. Den följer emellertid av relativitetsteorin, som är väl etablerad med andra observationer (se ovan). Den är emellertid kopplad till tidsdilationen. Föreställ dig myonerna som nämndes ovan. Sett i myonens koordinatsystem går tiden som vanligt, och myonen borde alltså sönderfalla innan den når jordytan. Motsägelsen försvinner om vi tar hänsyn till längdkontraktionen: sträckan myonen behöver tillryggalägga är mycket kortare pga längdkontraktionen. Nedanstående animering förklarar längdkontraktionen. Det finns massor med böcker om relativitetsteori och mycket på webben. Relativitetsteori - Resurser Animeringarna är gjorda av David M. Harrison, Dept. of Physics, Univ. of Toronto, se länk 1. Se även fråga 2697 Nyckelord: tidsdilatation [6]; relativistiskt massberoende [4]; längdkontraktion [6]; relativitetsteorin, speciella [45]; 1 http://www.upscale.utoronto.ca/PVB/Harrison/Flash/ Kraft-Rörelse [12742] 1 Hur långt är det mellan Sthlm & Malmö sett från rymdskeppet? 2 Hur långt tid tar det att resa mellan Sthlm och Malmö sett från rymdskeppet? 3 Hur långt tid tar samma resa sett från jorden? Skulle vara tacksam för svar.
Jag har fått fram några tankar själv men det är svårt. Svar: A och O är att inte blanda ihop koordinaterna för det rörliga och fixa systemet i Lorentztransformationen. Observera emellertid att du är fri att välja vilket system som är rörligt och vilket som är fixt. Låt koordinater med ' vara i rymdskeppet, koordinater utan ' på marken. Båda är överens om den relativa hastigheten v=0.95c (annars skulle inte relativitetsprincipen gälla). 1 Använd lorentzkontraktionen: l' = l/g där g = (1-v2/c2)-1/2. Eftersom g > 1 blir l' mindre än l. 2 Tidsdilatationen ger: t' = l'/v = l/g*v = t/g. Eftersom g > 1 blir t' mindre än t - tiden går långsammare. 3 t = l/v Observera emellertid att den relativa hastigheten är samma i båda systemen: v = l'/t' = l/g/t/g = l/t Nyckelord: tidsdilatation [6]; längdkontraktion [6]; relativitetsteorin, speciella [45]; 1 http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/tdil.html#c1 Kraft-Rörelse [2697] Svar: Först ett par definitioner: Längdkontraktion är den minskning i längd som enligt Albert Einsteins speciella relativititetsteori uppstår när ett föremål rör sig med stor hastighet i förhållande till den som mäter längden. Vid mer vardagsnära hastigheter är denna längdminskning helt försumbar. Det är först vid hastigheter som är minst 1/10 av ljusets hastighet som den får någon märkbar betydelse. Tidsdilatation (tidsutvidgning) beroende på hastighet innebär att om två referenssystem r och r', har identiska klockor, kommer en observatör i r att anse att klockan i r' går långsammare om referenssystemen r och r' befinner sig i relativ rörelse. En observatör i r' anser likaså att klockan i r går långsammare än den lokala klockan. Kosmiska strålningen består huvudsakligen av atomkärnor med mycket höga energier (mest väte). När de kolliderar med luften på cirka 20 km höjd, uppstår en uppsjö av olika partiklar. De flesta är kortlivade och sönderfaller snabbt. En av sönderfallsprodukterna kallas myon, och på grund av sina egenskaper, är den mycket lite benägen att kollidera med kärnorna i luften. Den försvinner för det mesta genom att den sönderfaller. Hur långt går den? Myonens medellivslängd är 2.2*10-6 s. Antag att den går nära ljushastigheten (300000 km/s). Då får vi en sträcka på 300000 * 2.2*10-6 = 0.6 km = 660 m. Ändå är det så, att de flesta partiklar vi kan registrera här nere är myoner. Genom en människa far det typiskt 30 - 40 högenergetiska myoner varje sekund. De överlever hit ner på grund av tidsdilatationen. De har så hög hastighet att tiden går mycket långsammare för dem, se översta formeln i bilden nedan. En myon med en Lorentz-faktor på 1000 kan i princip gå 660 km. Sådana myoner är inte alls ovanliga. För den myonen går tiden 1000 gånger långsammare (från oss sett). Jaha, OK men sett från myonen då? Där går ju tiden med "normal" hastighet och myonen kan väl inte hinna ner till markytan innan den sönderfaller? Jo, det gör den därför att längdkontraktionen, se nedersta formeln nedan, gör att den sträcka myonen måste tillryggalägga är mycket kortare (sett ur myonens perspektiv). Det är klart att resultatet att myonen hinner ner till marken innan den sönderfaller måste vara samma oberoende av om vi betraktar myonen från marken eller om vi följer med den ner genom luften. Se vidare Muon Se även fråga 1289 Nyckelord: relativitetsteorin, speciella [45]; längdkontraktion [6]; tidsdilatation [6]; Frågelådan innehåller 7624 frågor med svar. ** Frågelådan är stängd för nya frågor tills vidare **
|


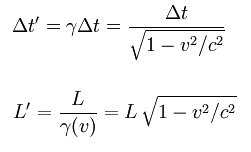
 Sök i svenska Wikipedia:
Sök i svenska Wikipedia:
