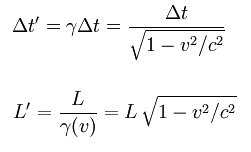Svar:
Kanske inte ett experiment, men ett bra exempel.

Först ett par definitioner:

Längdkontraktion är den minskning i längd som enligt Albert Einsteins speciella relativititetsteori uppstår när ett föremål rör sig med stor hastighet i förhållande till den som mäter längden. Vid mer vardagsnära hastigheter är denna längdminskning helt försumbar. Det är först vid hastigheter som är minst 1/10 av ljusets hastighet som den får någon märkbar betydelse.

Tidsdilatation (tidsutvidgning) beroende på hastighet innebär att om två referenssystem r och r', har identiska klockor, kommer en observatör i r att anse att klockan i r' går långsammare om referenssystemen r och r' befinner sig i relativ rörelse. En observatör i r' anser likaså att klockan i r går långsammare än den lokala klockan.

Kosmiska strålningen består huvudsakligen av atomkärnor med mycket höga energier (mest väte). När de kolliderar med luften på cirka 20 km höjd, uppstår en uppsjö av olika partiklar. De flesta är kortlivade och sönderfaller snabbt. En av sönderfallsprodukterna kallas myon, och på grund av sina egenskaper, är den mycket lite benägen att kollidera med kärnorna i luften. Den försvinner för det mesta genom att den sönderfaller. Hur långt går den?

Myonens medellivslängd är 2.2*10^-6 s. Antag att den går nära ljushastigheten (300000 km/s). Då får vi en sträcka på

300000 * 2.2*10^-6 = 0.6 km = 660 m.

Ändå är det så, att de flesta partiklar vi kan registrera här nere är myoner. Genom en människa far det typiskt 30 - 40 högenergetiska myoner varje sekund. De överlever hit ner på grund av tidsdilatationen. De har så hög hastighet att tiden går mycket långsammare för dem, se översta formeln i bilden nedan. En myon med en Lorentz-faktor på 1000 kan i princip gå 660 km. Sådana myoner är inte alls ovanliga. För den myonen går tiden 1000 gånger långsammare (från oss sett).

Jaha, OK men sett från myonen då? Där går ju tiden med "normal" hastighet och myonen kan väl inte hinna ner till markytan innan den sönderfaller? Jo, det gör den därför att längdkontraktionen, se nedersta formeln nedan, gör att den sträcka myonen måste tillryggalägga är mycket kortare (sett ur myonens perspektiv).

Det är klart att resultatet att myonen hinner ner till marken innan den sönderfaller måste vara samma oberoende av om vi betraktar myonen från marken eller om vi följer med den ner genom luften.

Se vidare Muon , Time_dilation och Length_contraction .

Se även fråga 1289 och fråga 2627

Nyckelord: relativitetsteorin, speciella [45]; längdkontraktion [6]; tidsdilatation [6];