Ursprunglig fråga:
Hej! Jag håller på och läser in kursen Fysik B och har problem med den matematiska rörelsebeskrivningen. I ett exempel som anges i kursboken är en matematisk modell över en 100-meterslöpares startförlopp:

v=10t-2.5t² samtidigt som t är mellan 0 och 2 sekunder (1)

Fråga: Hur långt har löparen enligt modellen kommit efter 2 sekunder?

I lösningen som anges börjar man med att utgå från regeln: ds/dt=v. Sedan anges, att s får bestämmas genom att göra en "primitiv funktion" till v, enligt:

s=5t²-2.5t³/3+C, där konstanten C sätts till 0 så att s=0 då t=0 (2)

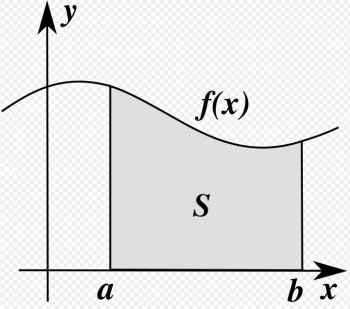
Mitt problem är att jag inte alls förstår hur denna "primitiva funktion" till v har bestämts. Hur får man stegvis fram denna funktion?? Hemskt tacksam för svar!
/Susanna A, Stockholm

Svar:
Susanna! Låt oss först beräkna accelerationen a = dv/dt. Hastigheten v ges av din ekvation (1). Derivatan av v med avseende på tiden t blir då

a = dv/dt = 10-5t

Anledningen till att accelerationen skrivs så här är ju att allteftersom löparens hastighet ökar, så måste accelerationen minska¹. Vi kan se att accelerationen enligt ovanstående modell är 0 vid t=2s. Då har löparen alltså uppnått sin sluthastighet. Om vi sätter in t=2s i (1) får vi slut(max)hastigheten 10 m/s.

Definitionen på hastighet är v=ds/dt. Hastigheten är alltså tidsderivatan vid en viss tidpunkt av den tillryggalagda sträckan. Se det så här: på den lilla tiden dt rör sig löparen sträckan ds. Hastighet är sträcka per tidsenhet alltså ds/dt.

Om vi våldför oss lite på matematiken kan vi se att ds=v*dt. Hastigheten v ges ju som funktion av t av (1). Vi kan då beräkna v for en massa värden från 0 till 2s och multiplicera med dt. Dessa ds kan vi sedan summera för att få den sträcka löparen tillryggalagt.

Matematiken bakom ovanstående kallas Infinitesimalkalkyl och utvecklades av Newton och Leibniz på 1600-talet (se Calculus och fråga 16084 nedan). Formellt är ds/dt något som kallas derivata. För att beräkna s från funktionen ds/dt måste vi integrera. Det finns massor med regler för derivering och integration (som man får lära sig i matematiken), men det viktiga i detta sammanhang är att integration är omvändningen till derivering. Så om vi integrerar ds/dt med avseende på tiden så får vi sträckan s.

Bilden nedan från Wikimedia Commons visar att integralen helt enkelt är ytan S under en funktion f(x). Integralen är alltså en yta, och räknas ut som en oändlig summa av pyttesmala rektanglar.

Hur får man då fram funktionen (2) från (1)? Ja, man måste kunna lite integreringsregler. Oftast är det emellertid enklare att derivera än att integrera, så låt oss kontrollera om (1) är derivatan av (2):

(d/dt)(5t²-2.5t³/3+C) = 10t-2.5t²

vilket alltså stämmer bra.

Det är naturligtvis måttligt intressant att beräkna hur en hundrameterslöpare spinger, men exemplet vill visa hur man i fysiken arbetar med matematiska modeller som sedan kan jämföras med verkligheten. Här är till sist en tabell med värden på a, v och s beräknade med ovanstående uttryck och med antagandet att löparen från 2 sekunder och framåt har den konstanta hastigheten 10 m/s.

  t     a     v      s
-------------------------
  0    10     0      0
  1     5    7.5    4.2
  2     0    10    13.3 
  3     0    10    23.3
  4     0    10    33.3
  5     0    10    43.3
  6     0    10    53.3 
  7     0    10    63.3
  8     0    10    73.3
  9     0    10    83.3
 10     0    10    93.3
 11     0    10   103.3

Hoppas detta hjälpte dig något!

¹ Till skillnad från en raket som accelererar snabbare och snabbare. Skillnaden beror på att för raketen är den största delen av massan bränsle, och detta försvinner ju efter hand som raketen accelererar.

Se även fråga 16084

Nyckelord: fysikalisk modell [12]; *idrottsfysik [42];