Vill du ha ett snabbt svar - sök i databasen
Hur mycket påverkas lodlinjens rikning av den centrifugalkraft som jordrotationen ger upphov till?
Fråga:
Om man står på marken bör man se till att hålla sin egen tyngdpunkt på en linje genom jordens tyngdpunkt och sina egna fötter, annars trillar man ikull. Men, hur muycket påverkar den centrifugalkraft som jordrotationen ger upphov till detta? Inte alls om man står på ekvatorn eller nord(syd)polen. Men i Skåne! Hur många grader (eller fraktioner av en grad) måste man luta sig "inåt" (dvs mot norr) för att inte falla ikull pga centrifugalkraften?
/Jon L, 2006-11-03
Om man står på marken bör man se till att hålla sin egen tyngdpunkt på en linje genom jordens tyngdpunkt och sina egna fötter, annars trillar man ikull. Men, hur muycket påverkar den centrifugalkraft som jordrotationen ger upphov till detta? Inte alls om man står på ekvatorn eller nord(syd)polen. Men i Skåne! Hur många grader (eller fraktioner av en grad) måste man luta sig "inåt" (dvs mot norr) för att inte falla ikull pga centrifugalkraften?
/Jon L, 2006-11-03
Svar:
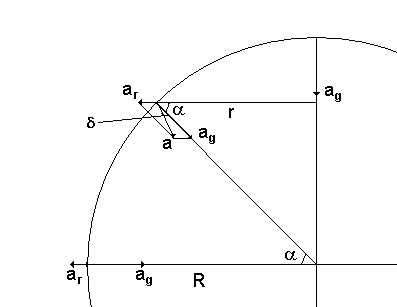
Jon! Det är en helt omärkbar effekt och det är knappast någon risk att man trillar, men låt oss som en övning räkna ut hur stor effekten är. Vi antar att jorden är klotformad och homogen med radien R. Den enda effekt vi tar hänsyn till är jordens rotation, vi bortser alltså från tillplattningen. Vi inför några beteckningar (se figuren):
ag = 9.822 m/s2 tyngdaccelerationen från jordens dragningskraft, se länk 1
ar accelerationen pga jordens rotation
a den resulterande tyngdaccelerationen
R = 6.37106 m jordradien
a latituden
w = 2p/(246060) = 72.710-6 s-1 vinkelhastigheten för jordens rotation
Vid polerna och ekvatorn är det ingen avvikelse i vinkel mellan a och ag (precis som du säger) medan det för medelhöga latituder är en avvikelse så att det är en liten "uppförsbacke" när man går norrut. Om du så vill kan du förstå detta som att "centrifugalkraften" försöker hindra dig att gå närmare rotationsaxeln.
Låt oss börja med att se vad som händer vid ekvatorn. Rotationshastigheten ges av
v = Rw = 6.3710672.710-6 = 463 m/s
Accelerationen pga rotationen blir
ar = v2/R = Rw2 = 6.37106(72.710-6)2 = 0.0337 m/s2
Tyngdaccelerationen vid ekvatorn blir alltså
ag - ar = 9.822 - 0.0337 = 9.788 m/s2
Accelerationen pga rotationen vid latituden a blir
ag = rw2 = Rcosaw2
Tillämpning av cosinuseoremet på triangeln ag, ar, a ger
a2 = ag2 + ar2 -2agarcos(a)
Den andra termen i högra ledet är mycket liten så vi kan försumma den. Vi får då
a = ag(1 - 2Rw2cos2a/ag)1/2 = ag(1 - Rw2cos2a/ag) =
ag(1 - 0.0337cos2a/9.822)
a = ag(1 - 0.00343cos2a)
Lodlinjens avvikelse från riktningen mot jordens medelpunkt d kan beräknas genom att vi tillämpar sinusteoremet på triangeln:
sind/ar = sina/a
sind = arsina/a =
Rw2cosasina/a =
Rw2sin2a/2a
Från detta uttryck kan vi se att avvikelsen är maximal för a=45o och noll för a=0o och a=90o.
Eftersom a är approximativt lika med ag och eftersom vinkeln är liten (sind = d) får vi
d = Rw2sin2a/2ag =
0.0337sin2a/(29.822) =
0.00172sin2a
d i grader blir
d = 1800.00172sin2a/p =
0.0985sin2a grader
Från detta kan vi se att lodlinjens maximala avvikelse (vid latituden 45o) är c:a 0.1o.
Jon! Det är en helt omärkbar effekt och det är knappast någon risk att man trillar, men låt oss som en övning räkna ut hur stor effekten är. Vi antar att jorden är klotformad och homogen med radien R. Den enda effekt vi tar hänsyn till är jordens rotation, vi bortser alltså från tillplattningen. Vi inför några beteckningar (se figuren):
ag = 9.822 m/s2 tyngdaccelerationen från jordens dragningskraft, se länk 1
ar accelerationen pga jordens rotation
a den resulterande tyngdaccelerationen
R = 6.37106 m jordradien
a latituden
w = 2p/(246060) = 72.710-6 s-1 vinkelhastigheten för jordens rotation
Vid polerna och ekvatorn är det ingen avvikelse i vinkel mellan a och ag (precis som du säger) medan det för medelhöga latituder är en avvikelse så att det är en liten "uppförsbacke" när man går norrut. Om du så vill kan du förstå detta som att "centrifugalkraften" försöker hindra dig att gå närmare rotationsaxeln.
Låt oss börja med att se vad som händer vid ekvatorn. Rotationshastigheten ges av
v = Rw = 6.3710672.710-6 = 463 m/s
Accelerationen pga rotationen blir
ar = v2/R = Rw2 = 6.37106(72.710-6)2 = 0.0337 m/s2
Tyngdaccelerationen vid ekvatorn blir alltså
ag - ar = 9.822 - 0.0337 = 9.788 m/s2
Accelerationen pga rotationen vid latituden a blir
ag = rw2 = Rcosaw2
Tillämpning av cosinuseoremet på triangeln ag, ar, a ger
a2 = ag2 + ar2 -2agarcos(a)
Den andra termen i högra ledet är mycket liten så vi kan försumma den. Vi får då
a = ag(1 - 2Rw2cos2a/ag)1/2 = ag(1 - Rw2cos2a/ag) =
ag(1 - 0.0337cos2a/9.822)
a = ag(1 - 0.00343cos2a)
Lodlinjens avvikelse från riktningen mot jordens medelpunkt d kan beräknas genom att vi tillämpar sinusteoremet på triangeln:
sind/ar = sina/a
sind = arsina/a =
Rw2cosasina/a =
Rw2sin2a/2a
Från detta uttryck kan vi se att avvikelsen är maximal för a=45o och noll för a=0o och a=90o.
Eftersom a är approximativt lika med ag och eftersom vinkeln är liten (sind = d) får vi
d = Rw2sin2a/2ag =
0.0337sin2a/(29.822) =
0.00172sin2a
d i grader blir
d = 1800.00172sin2a/p =
0.0985sin2a grader
Från detta kan vi se att lodlinjens maximala avvikelse (vid latituden 45o) är c:a 0.1o.
Länkar till externa sidor kan inte garanteras bibehålla informationen som fanns vid tillfället när frågan besvarades.
Denna sida från NRCF är licensierad under Creative Commons: Erkännande-Ickekommersiell-Inga bearbetningar

